
| ミラ型星の統計視差と個々のミラ型星の距離を用いて、その輻射、赤外 絶対等級を求めた。得られた輻射等級は最近の評価より平均して 0.5 等 暗かった。脈動定数の問題を論じた。 | 周期が 150 日より長いミラはおそらく第一倍音で振動している。それより 周期の短いミラは特異で、基本振動かも知れない。個々に距離が決められた ミラの実視絶対等級は Clayton, Feast による統計視差と整合する。 |
|
赤外測光 最近 Catchpole 1979 は近傍ミラ型星の J,H,K,L 測光を行った。ミラ型星の エネルギーはこの帯域でピークとなるので、彼の結果は輻射等級を求めるに使用 できる。 |
統計視差法を赤外に Clayton, Feast 1969 は統計視差法で実視絶対等級を定めた。ここでは彼らの 方法を赤外データに応用して、赤外絶対等級を求める。 |

|
統計視差は以下のステップで求める。
1.視線速度 ミラ型星の視線速度を Feast (1963), Feast, Woolley, Yilmaz 1972 から集める。吸収線データを用いる際はゼロに 近い、K-項を入れる。 2.固有運動 固有運動は Alden Osvalds 1961 から採る。赤外観測のある 178 星のみを 用いた。 |
3.太陽運動 Uo = 太陽運動の銀河中心方向成分 = 7.4 km/s、 Wo = 北銀極方向成分 = 7.0 km/s (Balona, Feast 1974) を用いる。 4.Clayton, Feast 1969 法 表1には、解に使用した Vo = 太陽運動の銀河回転方向成分, α = Uo 方向の速度散らばり, β = Vo 方向の速度散らばり, γ = Wo 方向 の速度散らばり, を載せた。解析の結果も表1にある。 |
|
距離が分かるミラには以下の種類がある。
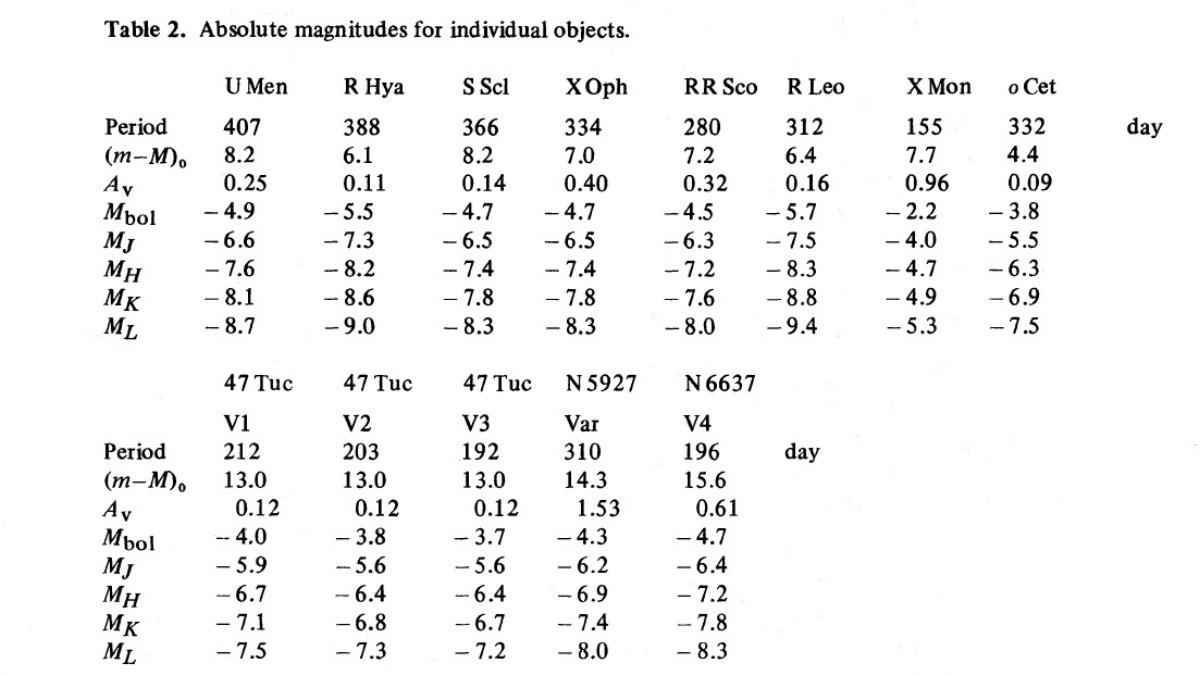
1.連星 R Hya (Eggen 1966), X Oph (Fernie 1959), U Men (Feast 1972) 2.星群 S Scl (Eggen 1970), RR Sco, R Leo (Eggen 1976) 3.三角視差 ミラ (Jenkins 1952) |
4.星間吸収線 X Mon (Keenan 1959) 5.球状星団 47 Tuc (Hartwick, Hesse), NGC 5927 (Lloyd Evans, Menzies 1977), NGC 6647 (Hartwick, Sandage 1968) 表2=結果 表2に個々のミラ型星の距離と等級を示す。 |
|
図1= Mbol と周期の関係 図1に Mbol と周期の関係を示す。表1、2のデータを使えば MJ, MH, MK, ML に対する同様のグラフが作れる。 RR Lyr から独立に結果を出したいなら NGC 5927, 6637 (距離に RR Lyr 使用) を外す方がよい。 長周期グループが暗い グループ 8, 7/8 はフィット線より低い。これ等の星は二重周期を示すもの が多いことと関連するのかも知れない。 距離既知ミラは明るい 距離既知の個々星の点はフィット線より上に多い。有意かどうか微妙。 Wood らの議論について Eggen 1975 の Mbol - P 関係は今回の結果より 0.75 等明るい。彼の結果は ここでも使用されている距離既知の4ミラに対する R, I 測光に基づいている。 Wood, Cahn (1977), Cahn, Wyatt 1978 はこの Eggen 1975 P-L 関係を使用しているので、彼らの 議論は明るすぎる光度に導く。 |
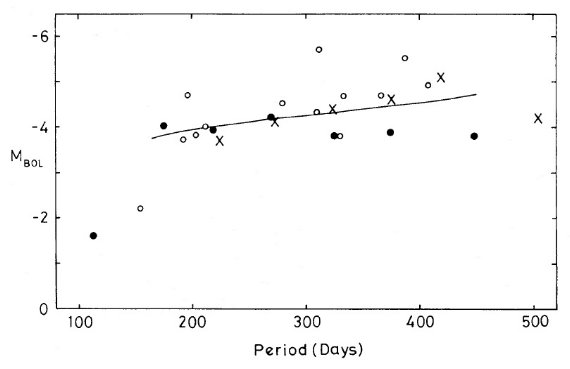 図1.Mbol と周期の関係. 黒丸=表1からの Mbol。バツ=表1からの M'bol。 白丸=表2から。 |

|
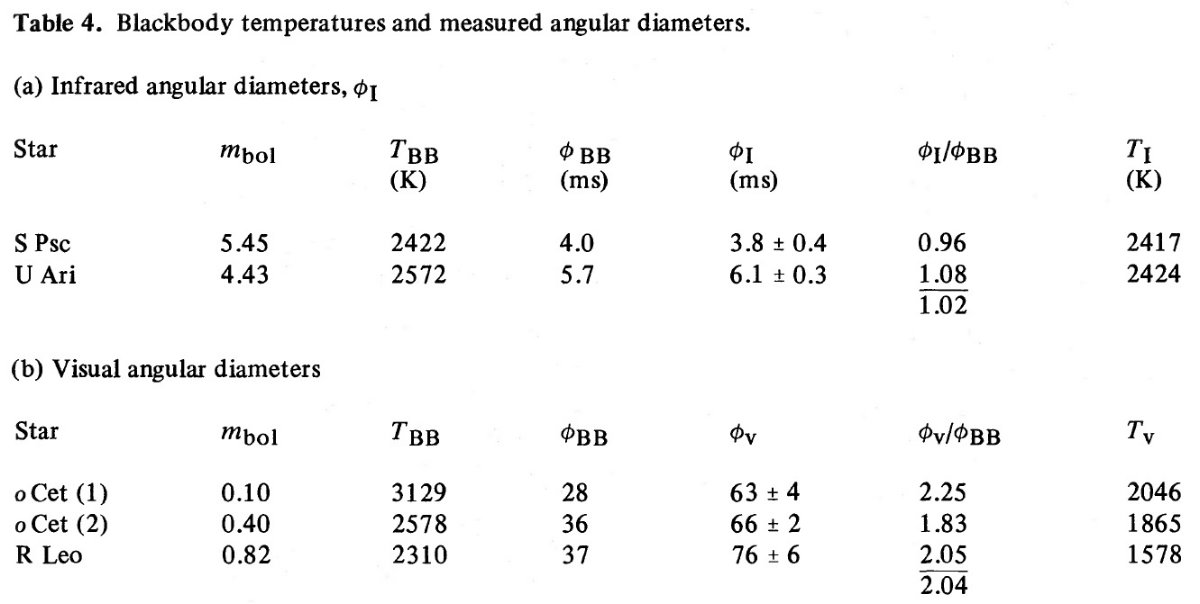
観測的 Q 図1から分かるように、P = 150 - 400 d で Mbol は長周期側 で僅かに明るくなる関係を示す。脈動定数 Q の評価は通常のように logQ = logP + 0.5 log(M/Mo) - 0.75 log(L/Lo) + 3 log(T/To) 代表的な Q を表3に示す。Mbolは表1から。質量は Feast (1963) の運動学的質量を用いた。TBB は JHK 黒体フィットで決まる温度 である。 P = 150 - 400 d の平均 Q = 0.065 である。Wood 1976 は モデル計算から倍音振動に Q = 0.04, 基本振動に Q = 0.1 を与えた。 モデル Q と観測 Q とを比較すると次の点が分かる。 モデル QBB の検討1=質量 ミラは激しいマスロスを経ているので、適用した運動学的質量は上限値と 看做される。さらに、 P = 375 d に適用した運動学質量 2 Mo はかなり怪しい。 過大評価しているかもしれない。質量が下がると Q も下がる。例えば 2 Mo から 1 Mo に下げると Q = 0.062 から Q = 0.048 になる。この値は第1倍音に 良く合う。 モデル QBB の検討2=角直径 TBB を Te として使うことに関しては正当化が必要である。 原理的には角直径の測定があるミラで調べればよい。しかし、スペックル干渉 計の結果では、角直径そして有効温度は測定波長で大きく変化する。エネルギ ー放射が高い波長帯での角直径そして有効温度を採るのが妥当であろう。 Ridgway et al 1979 は月の掩蔽を用いて、幾つかのミラ型星で H, K バンド角 直径を測定した。表4に赤外等級と赤外角直径を載せた。 |
表4(a) には
φI/φBB も載せた。表を見るとこの値が1に
近いことが明らかである。これは、この二星では、黒体温度が赤外有効温度に
近いことを示している。表4(b) の方には可視域でのスペックル干渉計による
角直径を示す。この場合には φV は φBB より
ずっと大きい。 φV を使って求めた有効温度は非常に低い値と
なる。
広がった大気の星における半径の意味 QBB はエネルギー放射ピークの近赤外で決めた角直径と整合する ことが判った。可視半径を用いると Q は低くなる。ミラのように広がった低 密度の大気を持つ星では、脈動計算においてどの半径を投入すべきは自明でな い。これ等の星の質量分布=密度分布が確定するまでは、この問題は Q の決定 における弱点であり続けるだろう。Hill, Willson 1979 による脈動の流体力学 計算は ο Cet と R Leo が Q = 0.1 - 0.11 の基本振動を行っている と結論した。我々の結論は、そのためには、つまり Q を 0.1 まで上げるには 我々が得た半径よりかなり小さな値=有効温度をかなり高くする必要がある、 ということである。 短周期ミラが基本振動? 短周期 P = 90 - 149 d ミラはちょっと変、と言われてきた。 Feast (1963) はそれらの運動特性が P = 300 d ミラと似ている事から、倍音振動と考えた。 しかし、それらの輻射絶対等級は周期の長いミラに比べ明らかに暗いので、 その可能性は低い。表3にある短周期ミラの Q は他グループの Q に比べ 3 倍 の大きさである。Wood 1976 によると、赤色巨星では Q(基本)/Q(倍音) = 3 - 5 である。これからすると、短周期ミラは基本振動星かも知れない。 |
| OH が観測されるのは大抵長周期なので、P ≥ 300 d サンプルについて、 視線速度に基づく統計視差と絶対等級を求め、表5に示す。輻射等級に有意な 差は認められない。 |
 表5.OHメーザーがあるミラと無いミラの Mbol |

|
Clayton, Feast 1969 と Foy et al 1975 Clayton, Feast 1969 は統計視差に基づいて、ミラ型星の実視絶対等級と 周期の関係を研究した。その後、 Foy et al 1975, Eggen 1975 が同様の 問題を調べた。Foy et al 1975 は 150 - 200 d グループは運動学的に非一様 ではないかと疑い、視線速度の大きい星を排除した。その結果、光度が低下 した。このグループの平均等級は Clayton, Feast 1969 では Mv = -3.0、 Foy et al 1975 では Mv = -1.8 と大きな差を生じることとなった。しかし、 短周期グループの視線速度分布が2成分であるという統計学的な証拠はない。 また、Foy et al 1975 の結果は球状星団のミラ型星の結果とずれる。従って 我々は短周期ミラは一様な集団であるという見解を維持する。 |
Eggen 1975 Eggen 1975 は表6に示す、距離が個々に知られた4つのミラ型星を調べた。 彼は周期に拘わらず Mv(median) = -1.25 という結果を得た。彼の平均はほぼ 変光位相 0.25 に対応する。Mv(median) は Clayton, Feast 1969 が統計視差 から求めた平均光度の等級 M'v(median) と一致しない。M'v(median) = +1.0(P=450d), -1.5(P=177d) である。しかし、Eggen の個々の星について、 彼の示した補正 (Mo-M) を施すと表6のような Mv(median) が得られ、 Clayton, Feast 1969 と良い一致を示す。 ( Mo-M の部分は Eggen 1975 を見 ても理解できなかった。マジック?) |