| 約30球状星団における Oosterhoff 周期シフト=周期-変光曲線の形の関係 から決まる、は二つのはっきり分かれたグループと言うよりは連続的な変化を 示すことが判った。シフトはメタル量と相関する:長い周期は低メタル星団に 起きる。論文 I, II からの結論では、変光星周期が長い星団では RR Lyr 絶対 等級が明るいことを要求する。光度レベルを ΔMbolRR = 3 Δlog P で規格化した 8 星団の合成色等級図から、主系列ターンオフ光度 はメタル量と ∂ΔMbolRR/∂[Fe/H] = 0.29 の関係 があることが判った。低メタル星団ほどターンオフ光度が明るい。この観測 観測結果は、下田、Iben がメタル量の異なる星団は同じ年齢であるという 仮定から計算したモデルの結果と一致する。[Fe/H] = [-2.3, 0] の星団データ をイエールモデルによる下田,Iben 条件を用いての解析は、全ての星団の年齢が 決定誤差 = 10 % の範囲内で一致することを示した。 |
星団が同年齢と言う独立な証拠は、水平枝等級とターンオフ等級との差を用
いても導かれる。データからは、高メタル星団 47 Tuc と NGC 6838 が低メタル
星団より若いことはあり得ない。ほぼ等年齢と言う条件からは、Oostethoff
周期シフトは正に観測されるメタル量との相関が導かれる。また、なぜ星団内の
星の周期-振幅関係がメタル量によって並ぶのかも、もし振幅が RR Lyr 不安定
帯の中の位置で一意に決まるとすれば、理解できる。 M3 RR Lyr の絶対等級を Mv = +0.80 とするなら、球状星団の年齢は 17 ±2 Gyr である。この年齢は、球状星団年齢に宇宙開始以来球状星団が 出来るまでの時間を加えれば、 Ho = 50 km/s/Mpc から決まる宇宙年齢と合う。 今回のデータは時折示されるもっと大きなハッブル定数とは明らかに矛盾する。 |
|
星団 RR Lyr の問題 RR Lyr に関する未解決問題に、 (1)Oosterhoff 周期シフトの原因 (2)水平枝レベルが [Fe/H] にあまり依らないのに、この周期シフトは [Fe/H] と強い相関がある理由。 (3)星団メタル量が低くなると、周期-振幅関係が長周期側にシフトする原因。 (4)このメタル量と関連する周期シフト Δlog P がフィールド RR Lyr にも起きる理由。 ここまでの成果 ここでは Sandage et al. (1981a) Sandage (1981b) で行った Oosterhoff 問題の検討を続ける。これまでに (a)水平枝光度の変化、ΔM (b)ΔM (c)個々の星での周期シフトへの他の唯一可能な説明は次のようである:ある Te で較べると、低メタル星団の変光星質量は高メタル星団より低い。 この要請は、現在の様々なメタル量とヘリウム量の星に対する ZAHB の計算結 果と逆センスで、かつその大きさが、計算結果の数倍大きい。したがってこの 説明はありそうにない。 |
(c)個々の星での周期シフトへの他の唯一可能な説明は次のようである:ある
Te で較べると、低メタル星団の変光星質量は高メタル星団より低い。
この要請は、現在の様々なメタル量とヘリウム量の星に対する ZAHB の計算結
果と逆センスで、かつその大きさが、計算結果の数倍大きい。したがってこの
説明はありそうにない。
P-L-A 関係 Sandage (1981b) では、周期-振幅関係のシフトは、もしも振幅が不安定帯上の位置で一意に決 まるとするなら、星団間の HB 光度の変化と同じであるとして理解できること が示された。さらに、P-A 関係と P-Te 関係とで周期シフトの大きさが等しい ことから、P-L-A 関係の存在が示唆される。 この論文でやったこと 本論文では、問題 (2) と (3) について論じる。フィールド RR Lyr 星の 問題は Sandage (1982b) で述べる。 第2章では Oosterhoff 周期グループは ΔP, [Fe/H], (B-V)o,g, ΔV1.4 に関して連続な分布を持つことを示す。第3章では 周期シフトが [Fe/H], (B-V)o,g, ΔV1.4 と相関することを 30 星団について示す。Δlog P(RR) を用いて規格化した合成 CMD を 第4章で示す。第5章ではこの HB 規格化が低メタルになるに従い明るくなる ターンオフ光度を与えることを示す。その上昇量は、もし星団年齢が等しいと 仮定したら、恒星進化モデルで与えられるものと同じである。第6章では 星団年齢が同一であることの他の証拠を示す。 |

|
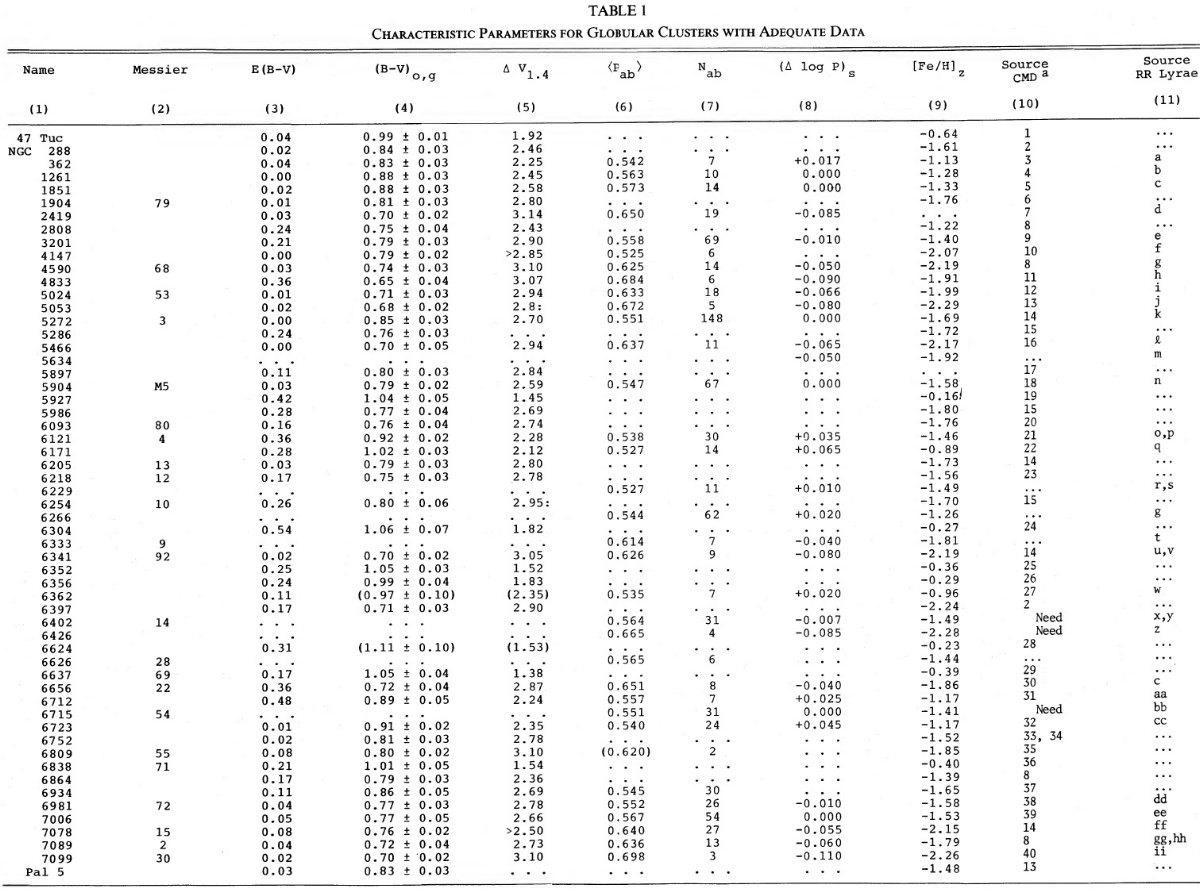
Oosterhoff 周期グループの提案 Grosse 1932, Oosterhoff (1939) は球状星団 RR Lyr の周期が二つのグループに分かれることを提唱した。二つ の平均周期は ⟨P⟩ = 0.55 と 0.65 d である。 表1=星団特性 1980 年からの文献検索で球状星団色等級図と RR Lyr 光度曲線を集めた。 表1にそれらを示す。E(B-V), (B-V)o,g, ΔV1.4 は文献値 の平均である。水平枝等級での巨星枝の赤化補正カラーは第4列、(B-V)o = 1.4 での赤色巨星枝等級は第5列に示す。第3列に使用した赤化量を示す。 第6列のタイプ ab 変光星の平均周期は Hogg 1973 から計算した。第8列の 周期シフト &Delta(log P) は、 Sandage (1981b) で定義されているように M3 が基準であるから M3 では 0.000 である。表1の 周期シフトは (Δlog P)s は増光期比率 Δφ rise - log P 図から定めた。"s" は変光曲線の形(shape)の意味 である。第9列の [Fe/H] は Zinn 1980 から採った。Zinn のゼロ点は Butler 1975a の直接 [Fe/H] 値に比べ 0.2 小さいことに注意せよ。 図1=表1の図解 図1は表1の図示で、以下のことが分かる。 (1)⟨Pab⟩ = [0.620, 0.698] と [0.525, 0.573] の二つの群れ に分かれる。これは Oosterhoff-Sawyer 二分化である。 (2)(Δlog P)s もまた二分される。各群れの内部では分布 は広がっている。 (3)パネル (c),(d),(e) には (B-V)o,g, [Fe/H]zinn, ΔV1.4 の分布を示す。パネル (c) には (B-V)o,g = 0.98 で跳びがある。それより赤い 星団には RR Lyr がないか非常に少なく、パネル (a), (b) から消えている。 それらか高メタル [Fe/H] > -0.6 星団である。名前を上げると、47 Tuc, NGC 5927, 6304, 6352, 6356, 6624, 6637, 6838 である。それらはパネル (d), (e) では左端に固まっている。 |
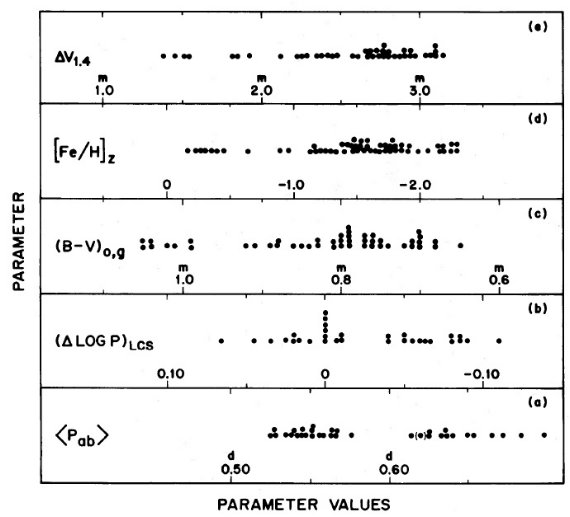 図1.表1の 4,5,6,8,9 列にある5つのパラメタ―のヒストグラム。パネル (a), (b) には Oosterhoff 二分化が見られる。パネル (c),(d),(e) では観測 エラーでそれが隠されているのかも知れない。Oosterhoff 間隙はパネル(c) では (B-V)o,g = 0.75, (d) では [Fe/H] = -1.7, (e) では ΔV1.4 = 2.7 に現れるはずであった。 |
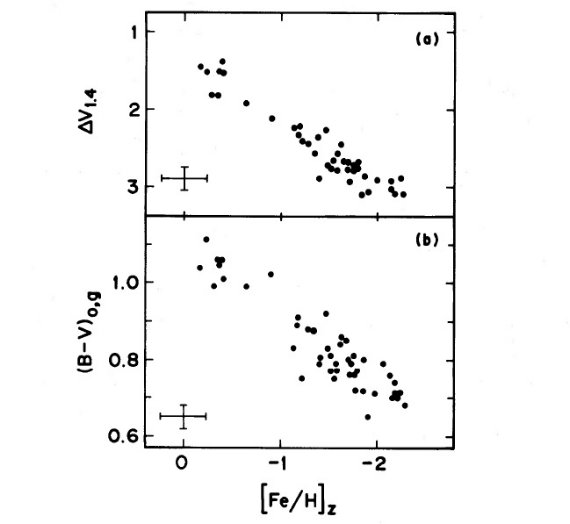 図2.上:[Fe/H] - (B-V)o,g 関係。下:[Fe/H] - ΔV1.4 関係。 図2= [Fe/H] - (B-V)o,g と -ΔV1.4 関係 図2には [Fe/H] に対して (B-V)o,g と ΔV1.4 の関係を 示した。相関はタイトで、 (B-V)o,g = 0.180[Fe/H] + 1.10 (1) と表される。 図3=別表現 図3には (B-V)o,g を横軸にして[Fe/H] と ΔV1.4 を較べた。図2でも図3でも Oosterhoff 分離は見えない。図1をよく見ると 分かるが、エラーが大きいためである。一方 (Δlog P) のエラーは 0.01 と小さいために検出されたのである。 メタル量ギャップ その代りに図2、図3には [Fe/H] = -0.8 を境界にしたギャップが現れた。 同じギャップが ΔV1.4 = 2 mag と (B-V)o,g = 0.9 に現れる。 明らかに、このサンプルでは高メタルサンプルはその形成史が未だ未知の、 中心が [Fe/H] = -2.2, -1.5, -0.3 の3つの Oosterhoff 群の一つである。 図4=(Δlog P)s と [Fe/H] の相関 図4上は(Δlog P)s と [Fe/H] の相関を示す。下は(Δlog P)s と (B-V)o,g の相関である。相関は以下の式で表される。 Δlog P = 0.116[Fe/H] + 0.173 (2) これはこの論文の主要な結果である。 |
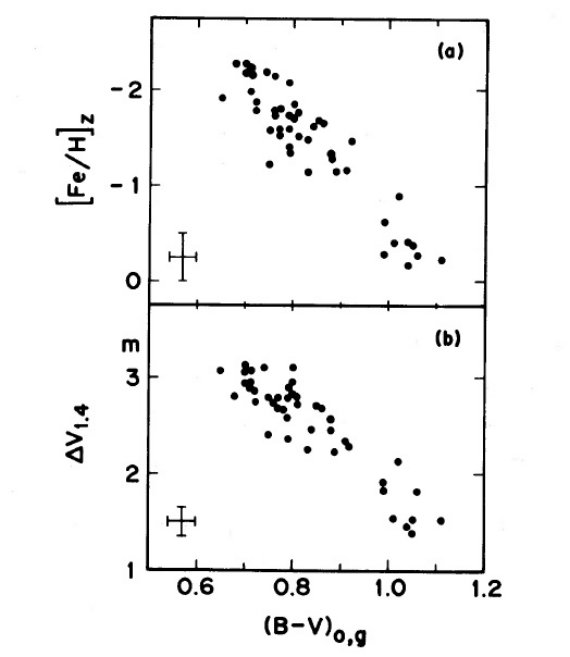 図3上:[Fe/H] - (B-V)o,g 関係。下:[Fe/H] - ΔV1.4 関係。 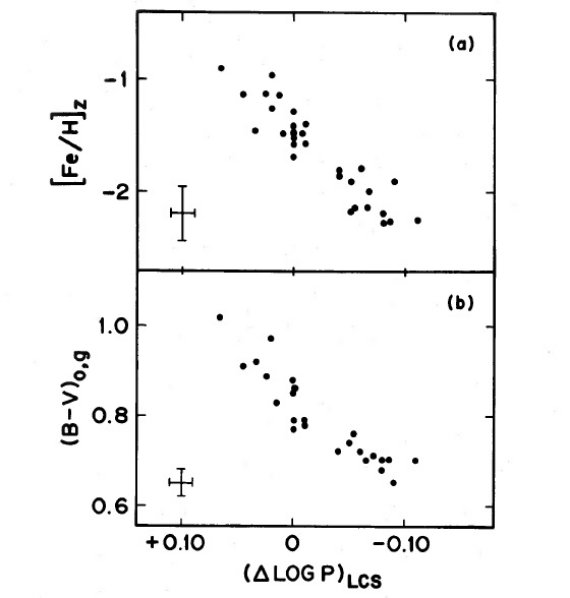 図4上:[Fe/H] - (Δlog P)s 関係。下: (B-V)o,g -(Δlog P)s 関係。(Δlog P)s = -0.04 付近が二つの Oosterhoff 群の境界に相当する。 |
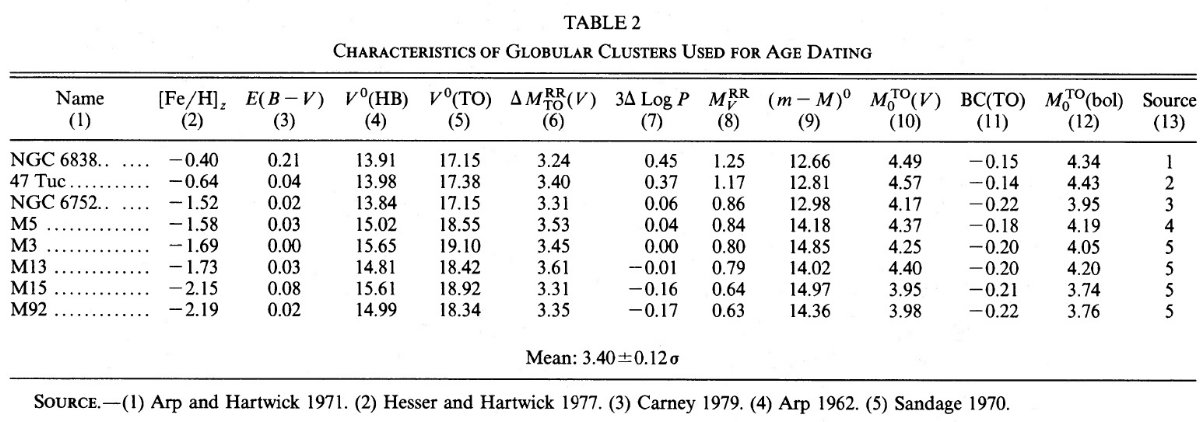
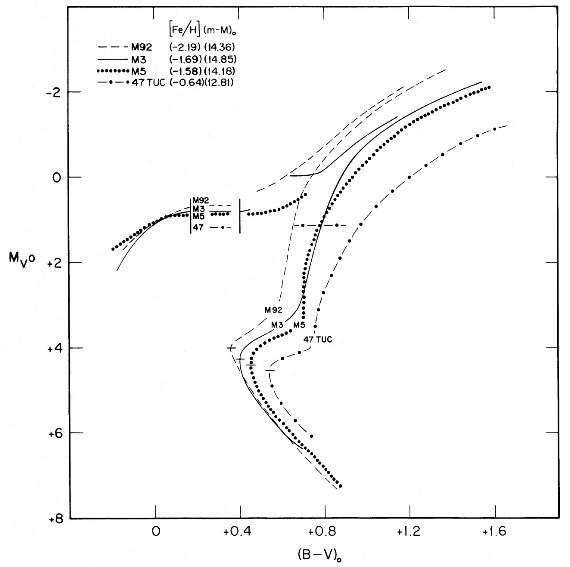 図6.メタル量が異なる 4 星団の合成色等級図。水平枝の規格化は表2 第8列から。主系列ターンオフ等級がメタル量の順になっていることに注意。 (規格化の意味が分からない。ずらして 重ねたわけでもないらしい。 ) 周期シフトから年齢まで 8球状星団には正確な色等級図があるので、主系列ターンオフ光度を使って 年齢を決められる。水平枝レベルが分かるとターンオフレベルが決まる。 水平枝の相対レベルは周期シフトから、ΔMbolRR = 3 Δ log P により決まる。絶対値の方は M3 の変光星絶対等級 Mv(RR) = +0.8 を 採用する。これは、 Sandage (1981a) で用いた値と少し違う。 表2=星団特性 表2は星団をメタル量の順に並べている。その第2列には Zinn 1980 からの メタル量を、第3列は表1と同じ赤化、第4,5列のは水平枝とターンオフの、 減光補正 = 3 E(B-V) した等級を載せている。それに使用した色等級図は第 13列にある。第6列は第4,5列から得た水平枝とターンオフの等級差を 載せた。 |
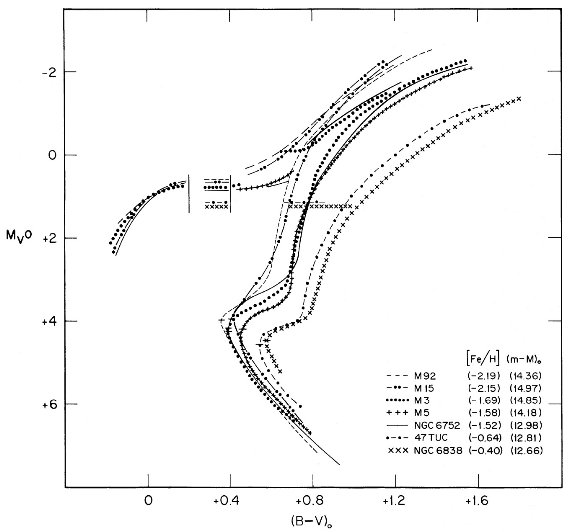 図7.全星団の合成色等級図。 この値はメタル量に依らず一定で、 ⟨ΔMv(TO-RR)⟩ = 3.40±0.12 は年齢の情報を与える。 第7列は式 (2) から計算した 3ΔlogP を示す。この値は M 3 でゼロに 規格化されている。第8列の MbolRR は第7列の 3ΔlogP = ΔMbolRR を M 3 での Mv(RR) = +0.8 に加えて求められる。 第8列と第4列から星団の距離指数が第9列に示される。 第10列は、第9列の距離指数を第5列のターンオフ等級に適用して求めた 主系列端末の絶対輻射等級を示す。第11列に示すターンオフ温度に対する輻 射補正は Carney, Aaronson 1979 から採った。ターンオフは主系列の最も青い 部分として決めた。 高メタルほど TO 光度低下 この水平枝規格化の結果を図6、7に示した。図6には、図7に見られる混乱 を避けるため、4星団だけプロットした。これ等の図を見ると、メタル量が上が るに連れて、主系列終端光度が暗くなっていくことが判る。 M 91 のターンオフ は M 47 に比べ ΔMbol 0.67 mag 暗い。平均すると ∂Mbol/∂[Fe/H] = 0.30 である。 |
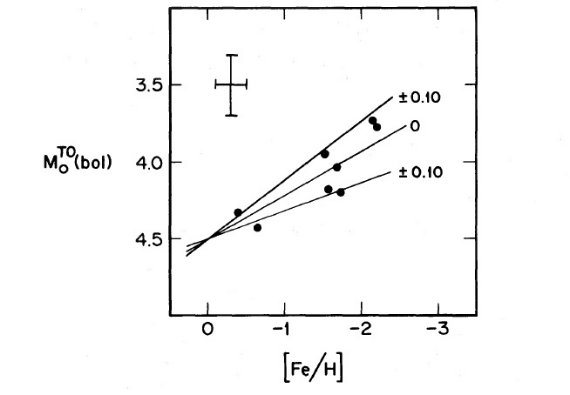 図8.8星団での主系列終端光度とメタル量との相関。実線=(多分 M 3) を 通る幾つかの ∂M/∂[Fe/H] に対する関係.ゼロを付けた線が、同一 年齢に対応する ∂M/∂[Fe/H] = 0.293 である。 図8=主系列終端光度とメタル量との相関 8星団での主系列終端光度とメタル量との相関を図8に示す。エラーバーは ±0.2 mag で、主系列終端光度を決める際の近似的なエラーである。 図中の線は 年齢差の比率 Δt/t 一定の軌跡である。ゼロとされるのは MTO と [Fe/H] 関係から要求される線である。 ターンオフ光度を決めるパラメタ― Ciardullo, Demarque 1977 の等時線から次の関係が得られる。 logt=10.2+0.41(MbolTO-3.81)-0.15([Fe/H]+2.3)-0.43(Y-0.3) (6) 従って二つの星団の年齢差は Δt/t = 0.944ΔMbolTO-0.345Δ[Fe/H]-0.99ΔY (8) 第3章の議論から Y と [Fe/H] は (6) 式のように逆相関である。 式(6) を (8) に代入して、 Δt/t = 0.944ΔMbolTO-0.277Δ[Fe/H] (9) この式は、もし二つの星団が同じ年齢を持つがメタル量が異なると、 ΔMbolTO = 0.293Δ[Fe/H] (10) ターンオフ光度のこのメタル量依存性は Simoda, Iben 1968, 1970 により、 ∂M/∂[Fe/H] = 0.32 として、年齢一定のための要請として、理論的 に発見された。これは式10と殆ど同一である。 観測される MbolTO と [Fe/H] の関係が図6,7に示されるよ うに、式 (10) と良く合うことから、8星団は同一年齢と言える。そして、 これが Oosterhoff-Sawyer 周期シフトがメタル量と相関する説明を与える。 図8には様々な ∂M/∂[Fe/H] に対する関係線を引いたが、ゼロを 付けた線が、同一年齢に対応する ∂M/∂[Fe/H] = 0.293 である。 |
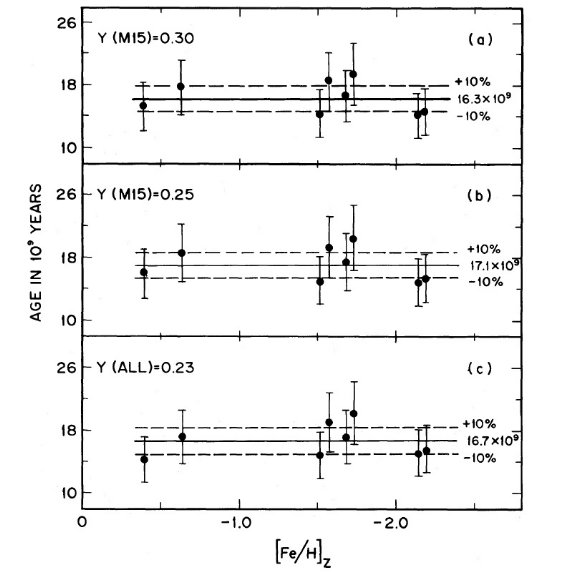 図9.8星団での主系列終端光度とメタル量との相関。 |

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|
