Ita18

Long Period Variables in the SMC （原稿）

板　その他

2015

　アブストラクト

　SMC 長周期変光星の可視と近赤外時系列データを解析し、その光度変化を調べた。脈動周期の間、光度変化は小さいことが判った。カラーに応じた輻射補正の値を求めた。光度変化と可視および近赤外変光との位相遅れが O-リッチミラに検出された。しかし、炭素星ミラと SRs には系統的な位相遅れは検出されなかった。

　明るいミラ型星にカラー位相の逆転が見出された。それらは長周期で、振幅が大きく、 O-リッチである。その原因は J バンドにおける TiO and/or VO 吸収帯が原因と思われる。周期・光度関係と周期・カラー関係を導き、示す。

　１．イントロダクション　

　２．データ　

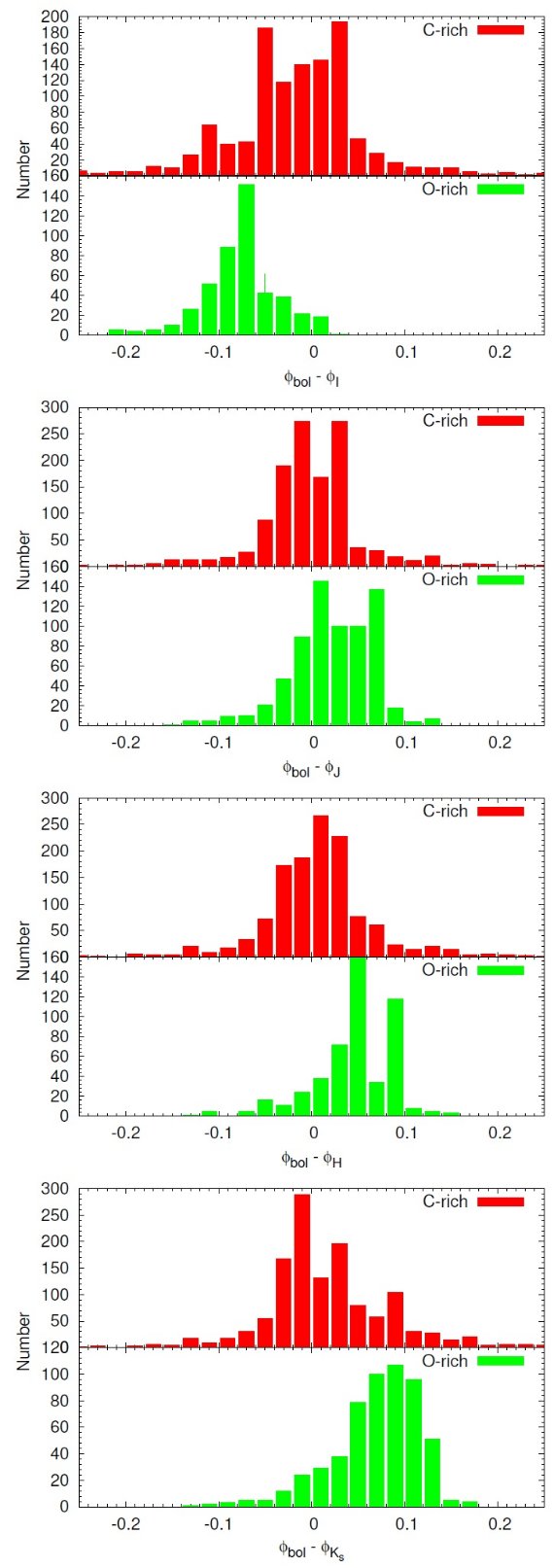
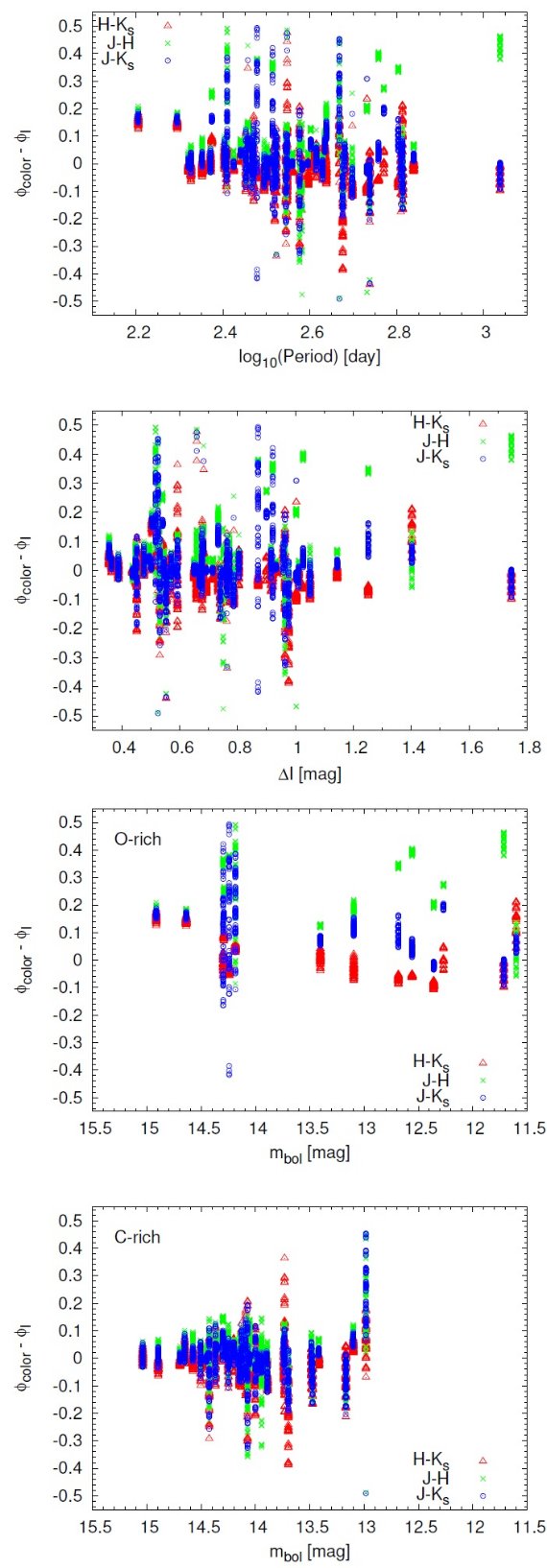
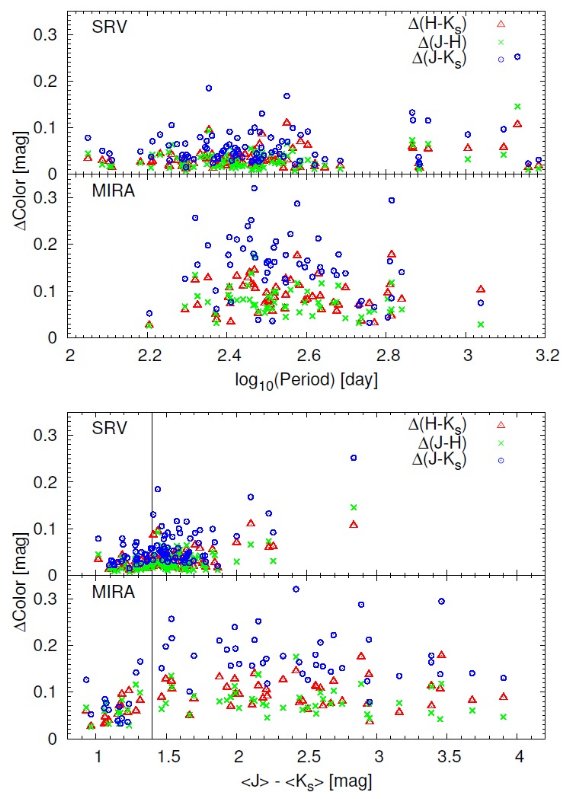
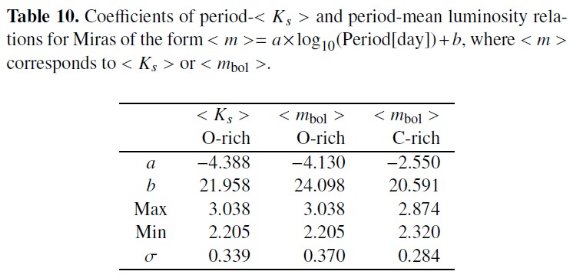
　２．１．可視　

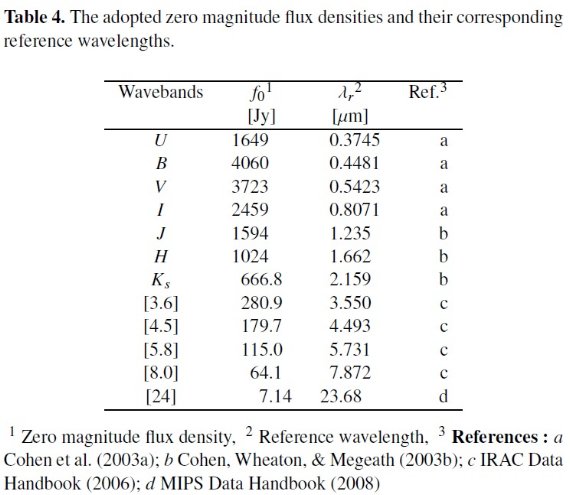
表１．

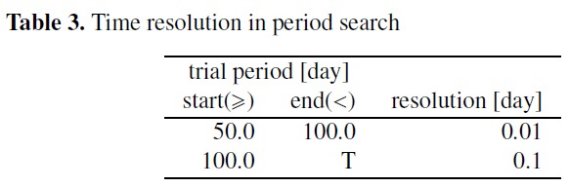
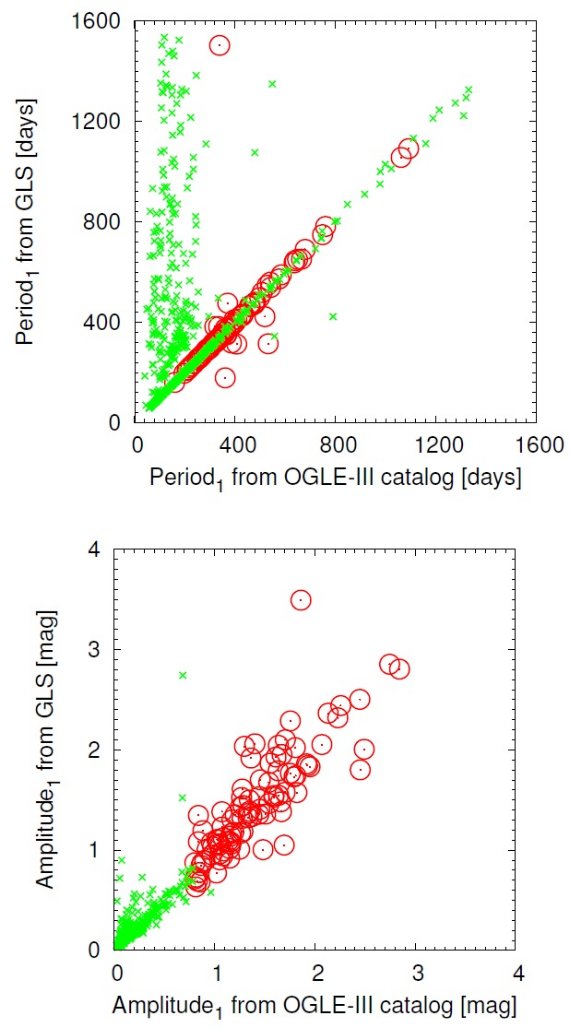
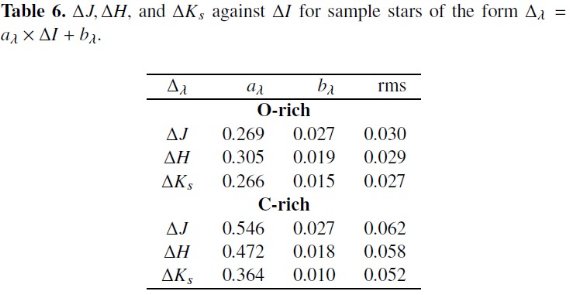
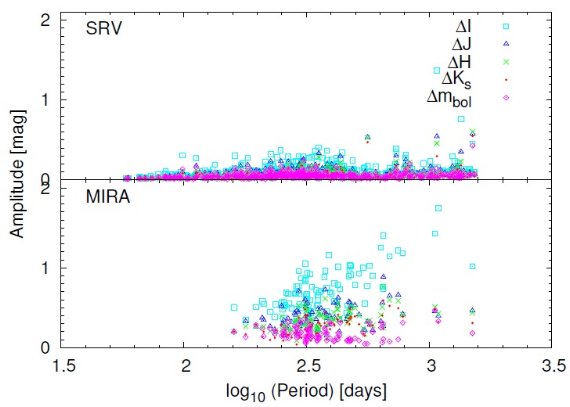
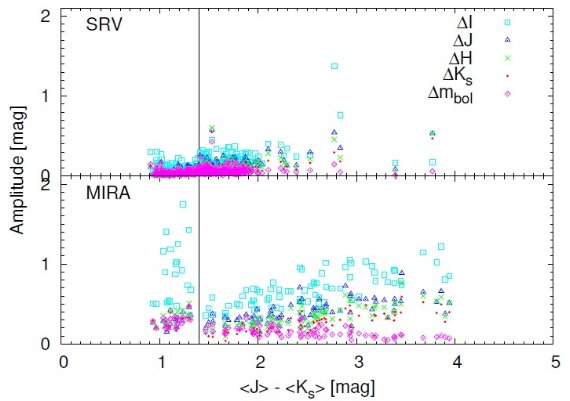
　OGLE-III 公開データから LPV でその中の "Mira" と "SRV" サブタイプを選んだ。Soszynski et al 2009 は I-バンドの山から谷までの巾が 0.8 等以上を　Miras, それ以下を SRVs と定義した。

　２．２．近赤外　
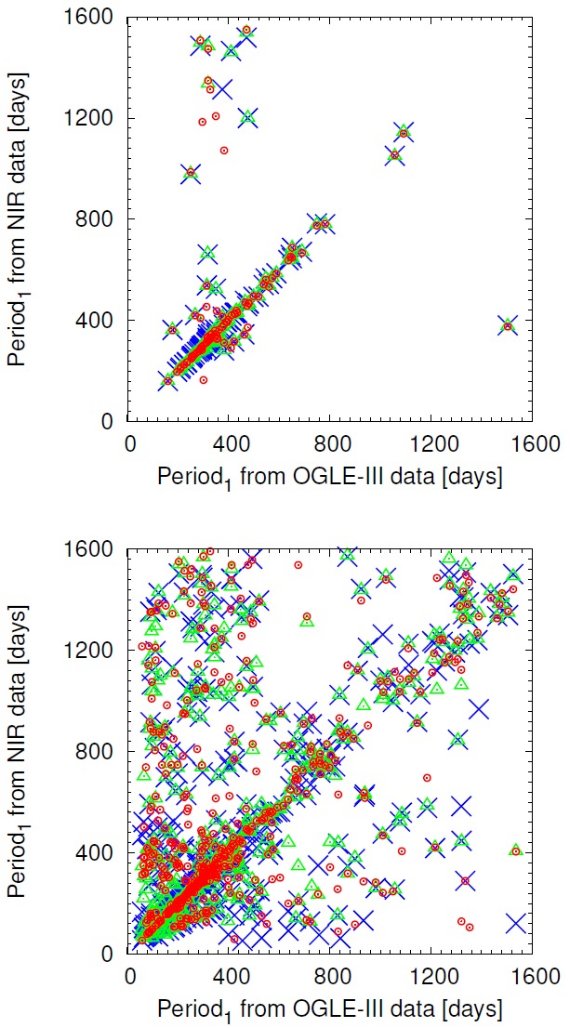
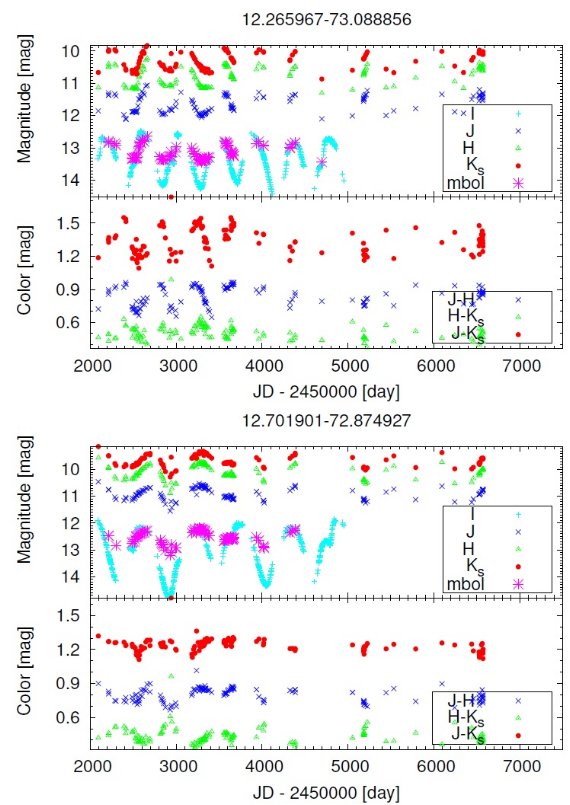
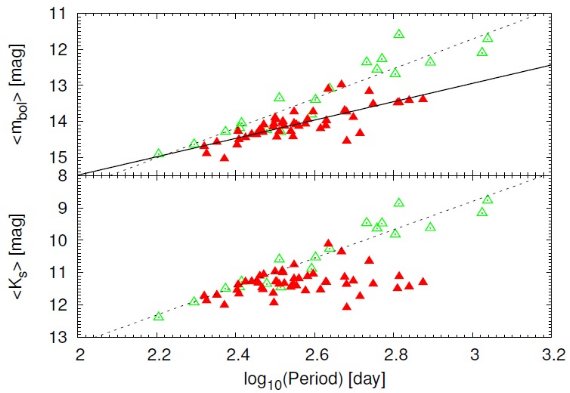
ＩＲＳＦモニター　

　Ita et al 2015 は 00h55m00.00s, -72°50^′00.00 ^″ を中心とする J, H, Ks モニターのデータを示した。彼らのサーベイ領域は OGLE-III に完全に含まれる。

　NIR 領域内の OGLE 天体　

　IRSF 領域内に OGLE-III カタログは 95 Miras と 514 SRVs を載せた。 12 SRV は IRSF 対応星がないが、内 10 個は実は領域のギリギリ外だった。残り２個は多分暗すぎて IRSF 検出限界外だったようだ。この二つは周期が 200 d と長く、Δ I = 1 mag で大きいので興味ある天体である。
( 0.8 等以上なのに SRVs? )
この先、 95 Miras と 514 SRVs をサンプル星と名付ける
( 12 SRV はNIR データなしで解析するのか？)

( IRSF LPVs は全て OGLE-III にあった？)

表２．クロス同定カタログ

　３．データ解析　

　３．１．周期、振幅、位相、フーリエ平均等級　

　GLS periodogram

　我々は Lomb 1976, Scargle 1982 の generalized Lomb-Scargle (GLS) periodgram 法を用いて周期サーチを行った。時系列データを (t_i, y_i, σ_i), i = 1, 2,..., N とする。

（１）サイン関数をフィット

　　　　　　　　y = a cos ωt + b sin ωt + c　　　（１）

　　　周期 P = 2π/ω である。

（２）誤差の二乗和の計算　

χ² = Σ N [y_i - y(t_i)]² 　　　　　（２）
i=1 σ_i²

　全観測期間を T としたとき、テスト周期 P = 50 - (2/5)T の間で χ² を計算した。表３に分解能をまとめた。

表３．周期探しの分解能

（３）多重周期を探すための pre-whitening

　まず、与えられた ω に対して 2ω, 3ω 成分を引いておく。
( 式で表して欲しい)
（４）FAP = false alarm probability

　　観測 t_i を変えずに、観測データをシャッフルする。そのシャッフルデータ系列に対して、GLS を行う。これを Ntotl 回繰り返し、χ² が "that of the period of interest" より小さい回数 Nchance を数える。 FAP = Nchance/Ntotal である。 FAP < 0.001 を有意と看做す。

　１年周期のギャップの影響　

　観測季節の関係でデータ系列に１年周期のギャップが生じる。変光周期が１年付近だとこのギャップが影響する。しかしそのような例は稀である。

　係数の決定　

　こうして、脈動周期 P₁, P₂, P₃, 振幅 A₁, A₂, A₃　と定数 c が決まる。
( c は一個？c₁, c₂, c₃　ではない？)

( 直交規格化関数で展開するだけではいけないのか？係数は積分だけで求まる。)

位相　

　位相 φ は φ = mod[(JD_i - JD_mean) /P₁] で定義する。JD_mean = ベストフィット GLS 光度曲線が上昇期に平均等級となる時期で決める。
( P₁, P₂, P₃ とその倍音部まで全部を足したもの？ )
この位相定義は印野たち 2014 がセファイドについて行ったのと同じ方法である。
( GLS 方は上述のどの範囲を指すのか？)

　３．２．ＧＬＳ法による周期、振幅の評価　

　３．２．１．OGLE I-バンド時系列データ　

図１．GLS 法で計算した P₁ と A₁ を OGLE-III カタログ値と比較。赤丸＝ミラ。緑バツ＝ SRVs.

　OGLE I-バンドデータに GLS 法を適用して、周期と振幅を求めた。それらを OGLE-III カタログと較べた結果が図１である。表示を合わせるため、計算した振幅は２倍にしてある。比較には P₁ と A₁ を用いた。
　全体としては GLS 法と OGLE カタログ値との一致は良い。しかし、 SRVs の中に GLS 方が長い周期を与える例がある。図２はその一例である。この星では GLS 法が 1254.8 d を与えたがカタログ値は 107.12 d であった。このこのように大きな相違が生じるのは "long secondary period" を持つ SRV に限られるようだ。"secondary" は "other than pulsation" の意味、または "after pulsation" の意味、または非常に長い光度変化の意味から来たらしい。脈動振幅は GLS と OGLE の間でよく一致している。
(GLS で 107 d 付近に P₂ でもピークが見えない。 )

( "secondary" の出所は？ )

( やはり、単純にフーリエ分解して、各ピークに意味を付与する方が明快でないか？)

図２．ＧＬＳの一例。星は OGLE-SMC-LPV-09790, SRV. 上：変光データ。中：GLS periodgram. 下：折りたたみ光度曲線 OGLE カタログの P₁ = 107.12 d は GLS から出た P₁ = 1254 d と大きく異なる。

　３．２．２．IRSF/SIRIUS NIR 時系列データ　
　ＳＲの問題　

　NIR データを GLS 法で処理した。図３ではミラと SRVs のそれぞれで OGLE と較べた。ミラでは少数の例外を除いて NIR と Opt データからの P の一致は良い。 SRVs の状況はもう少し複雑である。それらは

（１）可視周期＝近赤外の倍音周期。または逆のケース。

（２）LSP または非常に長期の変動を伴う星。

ただ、複雑な状況に関わらず、10 年以上の赤外データから長期変動, 1000 d 以上、の周期を決めることが可能である。

　OGLE/GLS 周期を使用する　

　図１と図３から我々の周期、振幅決定法は正しいことが判る。そこでこの先は OGLE 周期でなく GLS 周期を使用する。今後周期と言うときは OGLE I バンドデータを GLS 法で処理して得た周期を指す。OGLE を使う理由はこちらの方が観測密度が濃いからである。
( OGLE/GSL と IRSF/GSL の比較が必要？これでズレが見つかったら、精度または物理的要因？)

図３．NIR と可視での GSL と OGLE 周期の比較。上：ミラ。下： SRVs. バツ＝J, 三角＝H, 丸点＝Ks.

　３．３．輻射等級の計算　

表４．ゼロ点フラックスと参照波長。

I-データと J, H, Ks データの合体　

　サンプル星の SED ピークは I - Ks バンドにあると考えられる。それを念頭に置いて、OGLE-III の I バンドデータと IRSF J, H, Ks データを結合させた。観測時期にずれがあるが、最も近い観測値を使用した。多くの場合、ずれは 1 日以下である。

　見かけ輻射等級の計算１．内挿　

　４点の測光値を３次スプラインフィットして内挿値を決めた。
( フラックスで内挿か等級で内挿か？)
I 波長と波長 = 0 の間は直線でつないだ。
(こっちはフラックスで直線の意味？ )

　見かけ輻射等級の計算２．ゼロ点フラックスと赤化補正　

　赤化補正は Keller, Wood 2006 の E(B-V) = 3.2 と Schlegel et al. 1998 の Rv = 3.2 を使用した。
　カラー補正は行っていない。スペクトルデータが不足しているからである。 F(Mbol=0) = 3.055 10²⁸ Watts を使用した。図４には二つのミラ型星を例に見かけ輻射等級の変化を示した。

　長波長変光はなしと仮定　

　λ ≥ 3.6 μm での変光は無視する。将来 SAGE-VAR データが公開された時にはこの状況は改善されるであろう。非常に赤い星では長波長フラックス一定の仮定は正しくない。しかし、今回の可視で検出されたサンプルにはそのような星は殆ど含まれていない。
( 長波長側の SED をどう扱っているのかはっきりしない。Spitzer データを使用？)

図４．二つのミラ型星の、上：可視("light")と、下:近赤外のカラーと輻射等級の変化。

フーリエ平均輻射等級と振幅　

　最後にフーリエ平均輻射等級と振幅は前の節で述べたのと同じ方法で得られた。周期と位相も同じである。
(m_bol 時系列を GLS 解析？ )

( するとサンプルは IRSF 数になる。)

　４．議論　

　４．１．総光度の変光　

　４．１．１．可視、近赤外、総光度の振幅　

表５．主なブランケッティング分子。

　O-リッチと C-リッチはカラーで決める　

　以降は、角括弧でフーリエ平均を表す。また O-リッチと C-リッチの区別は Cioni, Habing 2003a, Cioni et al 2003b に従い、⟨ J ⟩ - ⟨ Ks ⟩ ≥ 1.4 を C-リッチとする。

　ブランケッティング分子　

　赤色巨星の変光振幅が可視では赤外または輻射等級の振幅よりずっと大きいことは知られている。Reid, Goldston 2002 を参照。これは分子ブランケッティング効果が時間と共に変化するためと理解されている。主な分子種 Lancon, Wood 2002 を表５に載せた。これを見ると、我々の J, H, Ks 変光データはどの分子が変光で主に効いているかを調べるのに最適と分かる。

（１）図５に可視と近赤外の振幅を、関係式の係数を表６に載せた。
　　　C-リッチ星の振幅の係数は O-リッチ星より大きい。

（２）C-リッチ星では可視も近赤外も C₂, CN, CO が吸収分子で共通。
　　　なので、可視と近赤外の変光は連動する。

（３）O-リッチでは可視は TiO で温度依存性が強い。このため、可視
　　　の振幅は非常に大きくなる。

図５．変光振幅の比較。赤＝炭素星。黒＝O-リッチ。十字＝ミラ。点＝ SRVs

表６．振幅間の関係式の係数。

図６．輻射等級の振幅に対するバンド等級の振幅の関係。黒破線＝ O-リッチ星。緑実線＝ Whitelock, Marang, Feast 2000 の銀河系 O-リッチミラの関係。

　輻射等級の変動は小さい　

　図６には輻射等級の変動に対する可視、近赤外等級の変動を比べた。まず気づくのは、ミラ型星の輻射等級の変動は小さいことである。輻射等級の振幅は 0.5 mag を越えない。つまり総光度の変化はファクター 2.5 以下である。図６には Whitelock, Feast, Marang 2000 による銀河系ミラの輻射等級と Ks 等級の関係も示した。表７には SMC O-リッチミラに対し同様の関係式を求めた結果を示す。C-リッチミラは複雑な分布を示し、単純な一次式でフィットするのは難しい。ただ、面白いのは同じ輻射等級振幅に対しては O-リッチ星と C-リッチ星が同じくらいの振幅を持つのは面白い。

　周期と振幅の関係　

　図７には周期と振幅の関係を示した。ミラには I-振幅が大きいものが多いが、近赤外、輻射等級にはその傾向が弱い。SRVs ではどの振幅も周期に関係なく弱い。

　カラーと振幅の関係　

　図８にはカラーと振幅の関係を示す。周期と違い、カラーと振幅の間にははっきりした傾向が見られる。⟨ J ⟩ - ⟨ Ks ⟩ が赤くなると振幅は大きくなる。O-リッチミラの輻射等級振幅は同じ傾向にある。一方、 C-リッチミラの輻射等級振幅はカラーに無関係に一定である。より赤い　⟨ J ⟩ - ⟨ Ks ⟩ > 3 の C-リッチミラの振幅はデータ不足で決められない。最も重要な特徴は、 C-リッチと O-リッチミラで ΔI の振る舞いが逆なことである。これは、おそらく分子の温度依存性が異なるためであろう。

図７．振幅と周期の関係。上：ミラ。下： SRVs.

図８．振幅と ⟨ J ⟩ - ⟨ Ks ⟩ の関係。縦実線＝ O-リッチと C-リッチの分割線。

表７．振幅間の関係式の係数。

　４．１．２．輻射補正とその位相依存性　

図９．BC_Ks と J-Ks の関係。下：ミラ。上： SRVs. 時系列の各観測毎に BC を計算した。

　BC_Ks は研究者により差がある　

　図９に J-Ks カラーと BC_Ks との関係を示した。他の研究者による BC_Ks も示してある。測光システムの違いに対する補正は加えていない。青破線はデータに２次式でフィットした結果である。緑と赤は（逆）C-リッチと O- リッチを示す。 J-Ks < 1.5 ではフィット線は他の研究結果と一致する。しかし、それより赤い側ではずれていく。ここに示した４つの研究のサンプルは, 我々が SMC RGs, Whitelock et al 2006, Kerschbaum et al 2010 は銀河系 C-星、 Riebel et al 2012 が LMC RGs と異なっているため比較が困難である。しかし、我々の波長帯は SED ピークをカバーしておりより信頼できる。図９はまた、ミラと SRVs との間に輻射補正の差があまりないことを示している。そこで、ミラと SRVs とを一緒にしてフィットした。表８にはその係数を載せた。表にはフィットを決めた際のカラーの最大値と最小値も載せた。残差の二乗平均は非常に大きい。そこで、表９には平均絶対等級と平均 Ks 等級から得た平均輻射補正のフィット式も載せた。残差は小さくなった。
(可視、中間赤外の貢献度を定量的に当たれないか？ )

図１０．図９と同じ。ただし、輻射補正を極小位相と極大位相で計算した。

　輻射補正は、有効温度、表面重力、組成により変化するはずである。
( 大気モデルではどうか？)
我々のデータはその影響を評価するには不十分であるが、輻射補正と位相の関係を調べた。そのため、サンプルを MAX 0.225 < φ_mbol < 0.275 と MIN 0.725 < φ_mbol < 0.775 との二つから採った。その結果を図１０に示す。我々の位相ゼロ点は上昇期の平均等級にとってあることを注意する。これを見ると輻射補正が位相であまり変わらない(chance?)ことが判る。
( 位相が変わるとカラーが変わるわけで、それとの関係は？)

表９．平均輻射等級と平均カラーのフィット係数。

　４．２．位相の遅れ　

　ミラに限定　

　Smith, Price, Miffett 2006 は銀河系(galactic?) の AGB 21 星の可視・赤外変光位相差を調べた。我々は SMC 95 Miras, 502 SRVs について位相差を調べた。図１１には可視、近赤外の位相差の頻度分布を示す。SRVs には系統的な傾向が見つからなかったのでミラについてのみ、示す。
( つまり、位相差には振幅依存性があるということか？)
SRVs に系統的な位相差が見られないという結果は Smith et al 2006 と同じだが、もしかするとこれは単に SRVs の光度曲線が複雑で位相ゼロ点が決めにくいことの現れかも知れない。

　O-リッチミラで位相差あり、C-リッチでなし　

　O-リッチミラでは可視位相は光度位相より 0.06 - 0.08 先行する。一方近赤外位相は後行する。これは Petti, Nicholson 1933 （！）と一致する結果である。ＩI- と Ks-位相の差は O-リッチミラでは 0.15 にまで達し、大きい。
( C-リッチまたは SRVs で φ_I-φ_Ks に系統的な差はないか？)
C-リッチミラの振幅が短波長ほど大きいことから判断すると、C-リッチミラは黒体的な SED を持っていて、その光度曲線は同じ位相で変動するようである。
( 変光に分子ブランケッティングが効いているという解説とどう整合させるのか？同じ分子種という説明？)

( 位相差は逆にした方が分かり易くないか？)

図１１．φ_bol - φ_I と φ_bol - φ_Ks の頻度分布。

図１２．φ_color - φ_I と周期、振幅、見かけ絶対等級との関係。

　４．２．１．位相逆転のあるミラ型星　
　近赤外で位相の逆転を示すミラ　

　Ita et al 2015 はミラ型星の中には近赤外で位相の逆転を示すものがあると指摘した。通常のミラでは光度が最大の時に近赤外カラーは最も青くなる。ある種のミラでは光度最大期にあるカラーは最も赤くなる。図４を見よ。

　φ_color

　φ_color のゼロ点はカラーが赤くなっていく際に平均カラーとなる時期とする。
( この「平均カラー」は前に定義していた平均等級の差で決めた平均カラーとは異なる？)

( この定義だと、等級の位相と１８０度狂ってしまわないか？)
すると、　φ_color - 　φ_I を周期、振幅、平均カラーなどと比べることが可能となる。　φ_I を基準に選んだのは、可視域では最も明るい時に最も高温だからである。Wing 1986.
( それが基準に選んだ理由なのはなぜか？)

　J-H カラーに位相逆転　

　図１２にその結果を示す。明らかに、O-リッチミラでは J-H カラーに位相逆転が見られる。幾つかの星では J-Ks にも逆転が起きている。星が最も高温と思われる時期に J-H カラーは最も赤くなる。log P > 2.7, ΔI > 1.0 の O-リッチミラでは J-H カラーの位相変化が大きい。全ての O-リッチミラでこの位相逆転が起きるわけではないらしい。これは、J-H は、またある種の星では J - Ks も、温度指標としてあまり良くないことを示すものである。
( SED 主要部でカラーが赤くなるのに、温度が高くなることがあるのか？)
炭素星ミラのカラー変化は正常であり、常に光度が増す際にカラーは青くなる。
( カラー逆転は振幅が長波長側で大きくなるためなのか、それともバンドで位相が移動するためなのか？どういう表示だとその差が明らかにできるか？)

　４．２．２．カラー変化と振幅　
　図１３はカラー変化の振幅が周期と無関係であることを示している。 O-リッチミラのカラー振幅は周期に関係なく 0.05 等程度である。 C-リッチミラのカラー振幅はカラー毎に代わり、O-リッチみらより大きい。
(等級振幅とカラー振幅を比べるべきでないか？ )

図１３．カラー振幅と周期（上）、平均カラー（下）との関係。

　４．３．他の雑多な結果　

　４．３．１．ミラの周期等級および周期光度関係　
　星周ダストの影響　

　ミラの周期等級関係がダスト星で破綻するのは良く知られている。 Whitelock 2012 は O-リッチミラではそれが非常に長周期になって生じるが、 C-リッチ星では非常に広い範囲の周期に渡ると述べた。
( どちらも 400 d からではないのか？)
周期光度関係ならばダスト減光の影響は受けないであろう。

　Ks-、m_bol- 周期関係　　

　図１４にはミラ型星の　Ks-、m_bol- 周期関係を示す。C-リッチ星はおそらく星周ダストの影響で線形の周期-Ks 関係を見出すことは難しい。我々のサンプルには大きな星周減光を持つ O-リッチミラは含まれていないようである。線形フィットを、 O-リッチミラの P-Ks 関係、O-, C-ミラの P-m_bol 関係に行った。表１０にその結果を示す。

表１０．ミラ型星の周期等級関係フィット式の係数。

図１４．ミラ型星の周期等級関係。緑＝O-リッチミラ。赤＝C-リッチミラ。点線と実線はそれぞれのフィット。

　４．３．２．周期・カラー関係　
　O-リッチ星は固有カラー

　周期カラー関係は星間減光を求めるのに有用である。図１５にミラと SRVs に対するかなりきつい関係を示す。ミラと SRVs とでは大分傾向が違うことが判る。 C-リッチか O-リッチかも関係に影響している。SRVs では組成と周期に関係なく一定のカラーを示している。O-リッチミラの NIR カラーは弱い周期依存性を示す。一方、可視-近赤外カラーは周期に依存する。これは、O-リッチ星周ダストが NIR では透明であること Woitke et al 2006 で説明される。また、同時にその近赤外カラーは固有カラーをほぼ正しく表していることも示唆する。

　C-リッチ星のカラー　

　C-リッチ星のカラーは強い周期依存性を示す。そのカラーは星周ダストの赤化を受けていることを前節で示した。これは C-リッチダストが可視でも近赤外でも不透明なためである。この緊密な周期カラー関係は周期と質量放出率に関係があることを示している。実際、 Wood 2007 は質量放出率と周期に強い相関が、特に P > 500 d では、あることを指摘した。我々の得た、周期カラー関係は周期の短い星でさえ、周期と質量放出率には強い相関が存在することを示している。フィットの係数は表１１に載せた。

図１５．周期・カラー関係。上：可視と近赤外間のカラー。下：近赤外カラー。三角＝ミラ。丸＝ SRVs. 赤＝C-リッチ。緑＝O-リッチ。点線と実線はそれぞれのフィット。
(緑三角＝O-リッチミラがない。 )

表１１．周期-カラー関係の係数。

　５．まとめ　

　SMC 赤色巨星変光星の可視と近赤外の時系列測光データをつなげて解析した。その結果、以下の様子が明らかとなった。

（１）輻射補正

（２）位相差

（３）カラー逆転

（４）周期-光度関係

（５）周期カラー関係