|
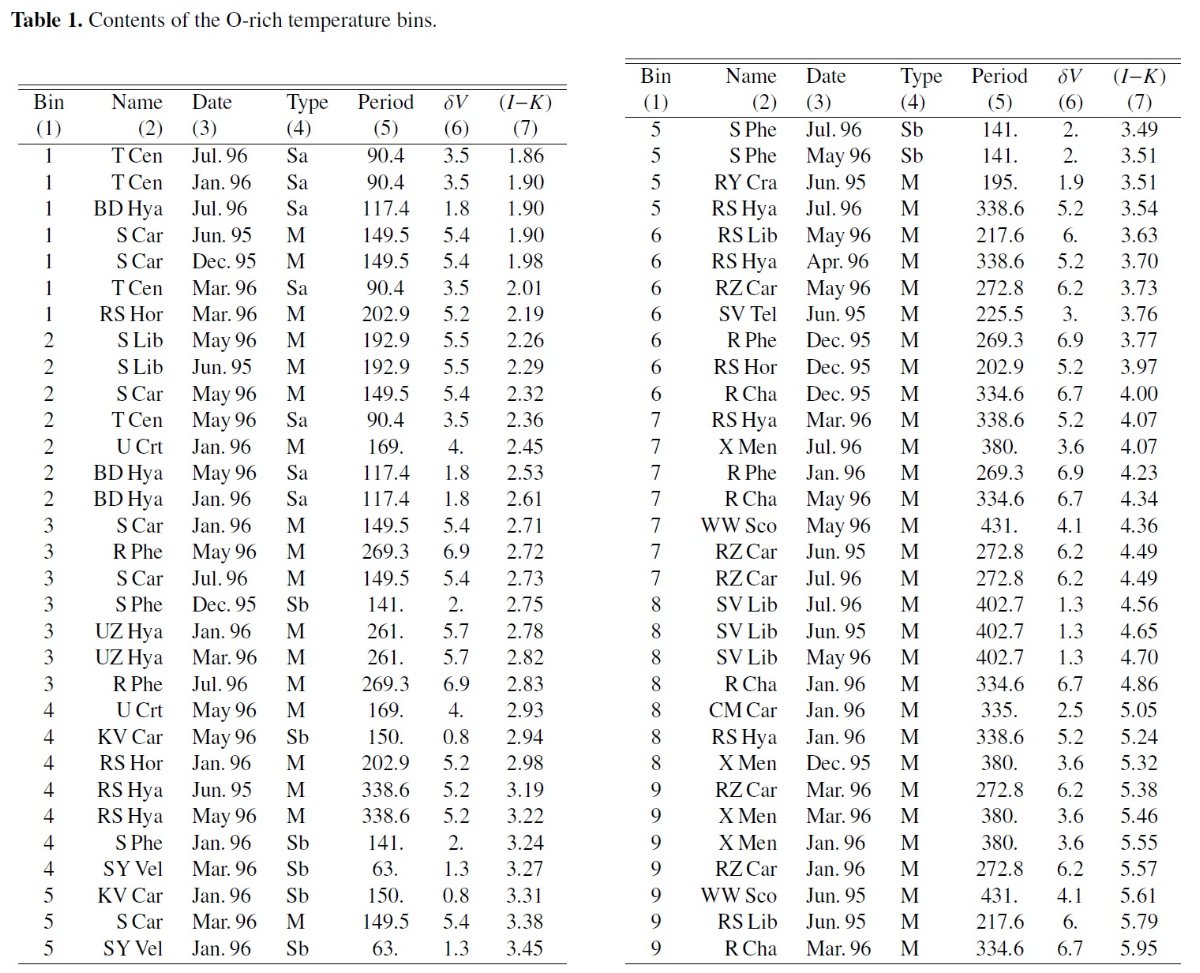
上部 AGB は星毎のスペクトルに差が大きい 上部 AGB は O-リッチと C-リッチな長周期変光星に占められている。中間年齢 星集団の近赤外光は実質的にこれらの星の光が主成分である。個々のこれ等の星の スペクトルはばらつきが大きく、それらを直接に銀河光の合成サンプルに使う訳には いかない。 平均スペクトルの作成 Lancon, Wood 2000 の個々星のスペクトルライブラリーを用い、種族合成に 用いるための平均スペクトルを作成した。平均スペクトルと進化経路との関係を論じる。 スペクトルの特徴とカラーとの相関 LPV 星スペクトルを並べて、平均を求める区間を定めるため、分光測光的特徴 の間の相関を再検討した。可視域での特徴と I-K のような可視連続光カラーの間にはよい 相関が存在するが、可視域指数と近赤外カラーの間には大きな散らばりがある。 |
広帯域連続光のカラー温度は分類に適している この散らばりの原因の一部は、個々の星の何回かの観測を HR 図上にプロット してみると分かるが、 LPV 自体が幅広なことである。広帯域連続光のカラー温度は分類に 最も適していることを論ずる。得られた平均スペクトルの系列は、確かに規則正しい変化を示した。 いくつかの注意 (1)BC と温度スケールはスペクトルをモデル進化経路上の点と対応させるのに必要。 (2)平均スペクトル作成の際に使った簡単化の仮定。 (3)サンプルバイアス (4)銀河の星間水素輝線への小さな寄与 |

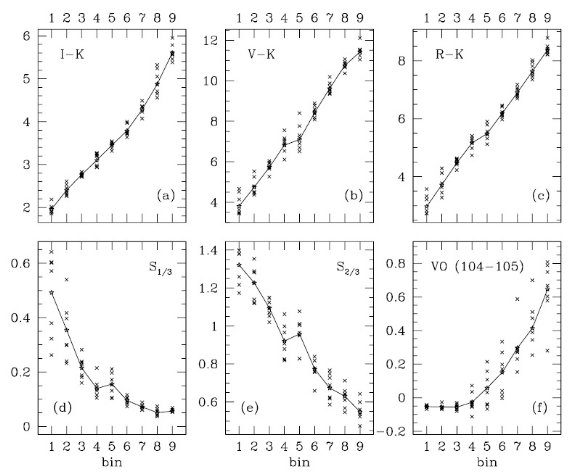 |
図1.(I-K) に基づくビン番号に沿っての温度鋭敏な指数の変化。 バツ印= Lancon, Wood 2000 の O-リッチ LPV.実線=平均値ライン。 当然だが、 (a) ではバツ印は縦には重ならない。(b), (c) の分散が 小さいことは (V-K), (R-K), (I-K) が共通の情報を含んでいることを 示す。(f) VO は VO A-X($Delta;v=0) バンド 1.05 μm の深さ。この 分子バンドは高温 LPV に存在しないので温度指標として不適当。(d) S1/3, (e) S2/3 は Flux 1994 が定義した指数。 静的巨星ではスペクトル型の良い指標だが、> M6 では S1/3 は飽和する。 |
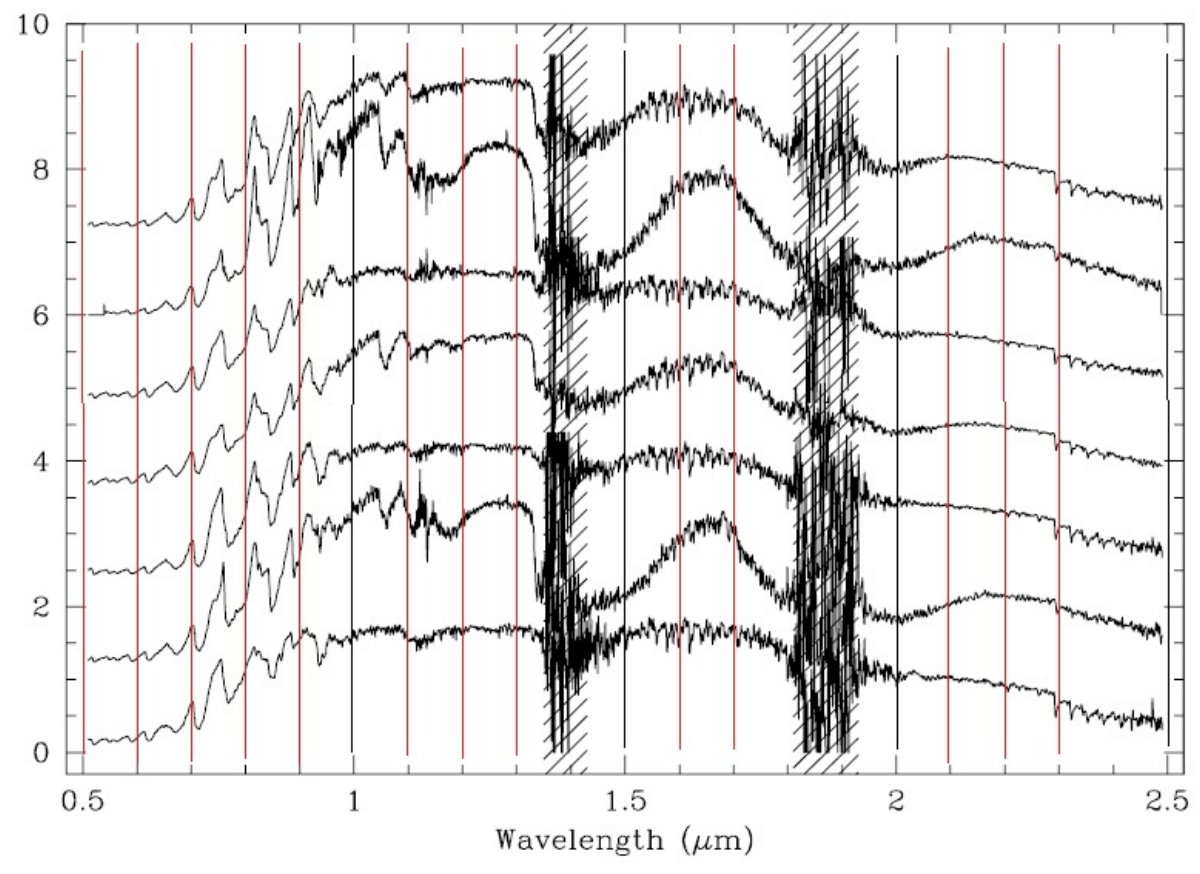
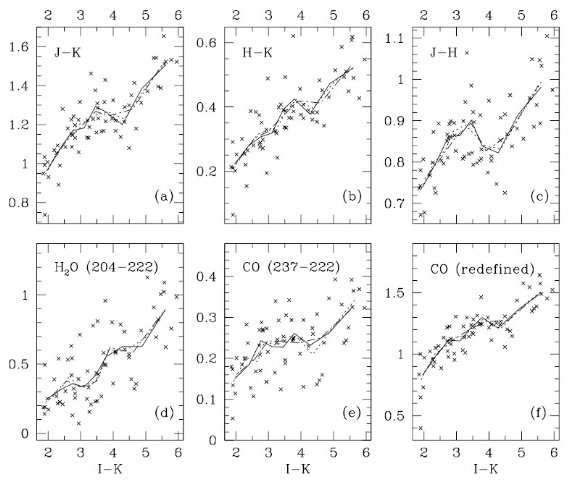 | 図3.近赤外スペクトル指数と (I-K) の関係。線=平均スペクトルの値。 (a),(b),(c) の赤外カラーは (I-K) と大体相関するが分散が大きい。 もし、(I-K) が O-リッチ LPV 温度と相関がよいとしたら、近赤外カラー は温度の良い指標になり得ない。近赤外で作ったビンはスペクトル型の 巾やエネルギー分布が広がり過ぎる。ビン 5 - 7 にかけて、近赤外カラー の逆転が生じるのは、温度と分子吸収の効果が競合する結果であるがもっと 大きなサンプルで確かめる必要がある。。 (d), (e) は HST/NICMOS F204M, F222M, F237M 撮像の結果。(f) CO は カラー補正を施してある。 |
|
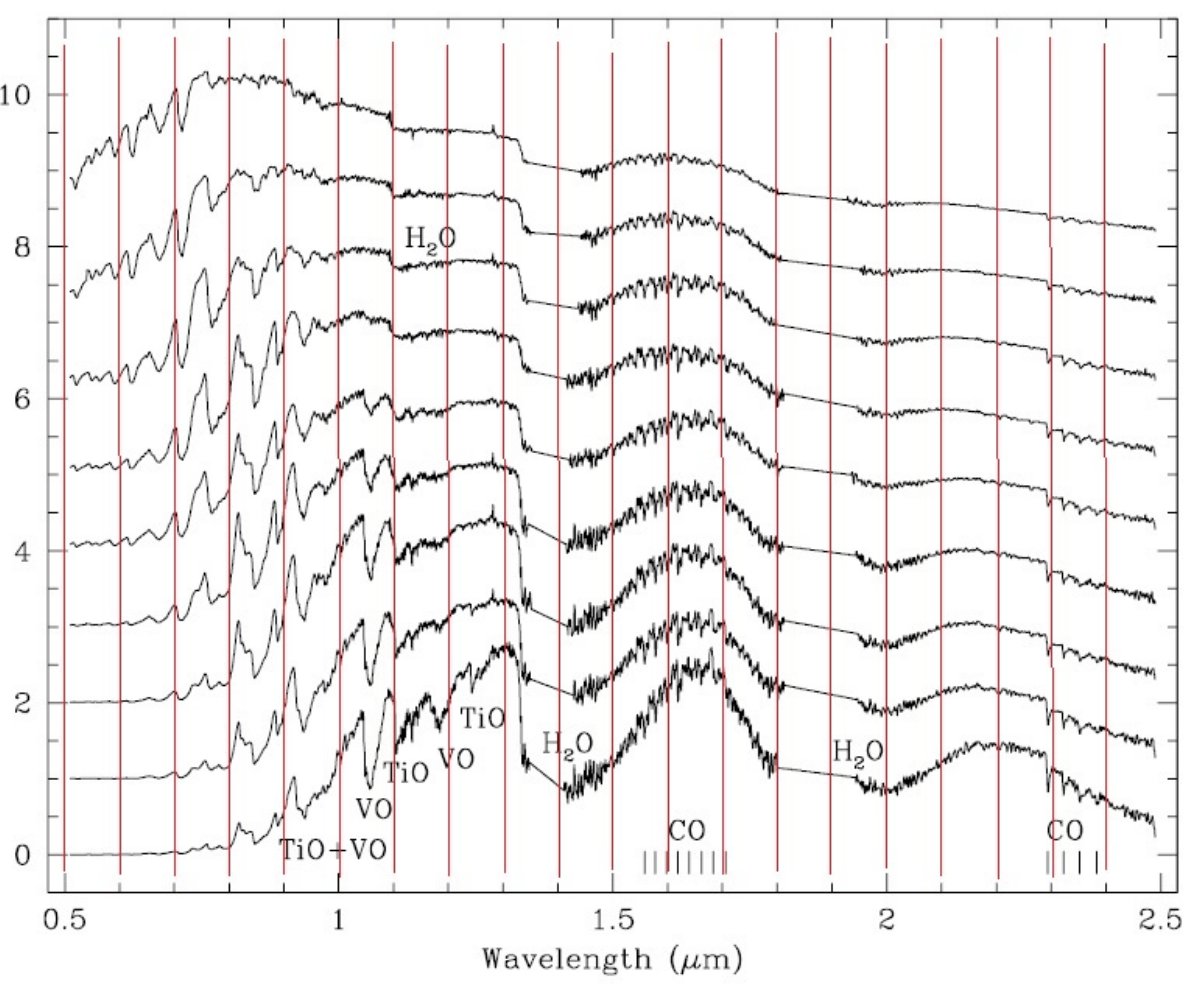
水 指数 上の図4はビン=5に含まれる 7 つの LPV のスペクトルを並べたものである。 大気の最も遠い部分で形成される水が脈動で決まるその時の大気構造に鋭敏に 反応しているかが分かる。水指数は H2O = -2.5log[Fλ(F204M)/Fλ(F222M)] - H2O(Vega) で与えられる。Fλ(F204M) は H2 バンドの中央、 Fλ(F222M)は準連続光部のフラックスである。図3 (d) のデータ点分布の下縁は H2O バンドが弱いか存在しないかの 星に対するカラー温度変化に過ぎない。ある (I-K) で (204-222) の差は最大 0.7 mag に達する。 CO CO 指数は次の式で定義される。 CO = -2.5log[Fλ(F237M)/Fλ(F222M)] - CO(Vega) |
CO の相関、図3(e)、は悪い。CO バンドは赤い星ほど強いが、しかしその連続光部分の変化は
分子吸収も強くなるために相殺されてしまう。図3(f) はカラー補正を加えてある。
Fλ(F222M)は、F165M(1.65μm) と F222M(2.22μm) から
外挿した 2.37 μm での値で置き換えられている。こうすると、
(I-K) と COredef との強い相関が現れてくる。実際 COredef には
通常の CO 指数と (H-K) カラーの情報が結合されている。この結果、通常の CO, H-K の
どちらよりも COredef と I-K との相関は良くなった。
静的巨星と超巨星の CO 静的巨星は I-K = 2 - 3.1, 超巨星は I-K = 2.7 - 4.5 である。図3d を見ると、 H2O 指数 < 0.29 である。静的巨星の CO 指数は図3e, f で LPV 平均ラインの 上に乗る。一方、超巨星は LPV より上の方に散らばっている。 驚いた! O-リッチ LPV の赤外特徴がこんなに散らばっているのに、平均スペクトルにすると これほど規則性が現れたのは驚きであった。 |
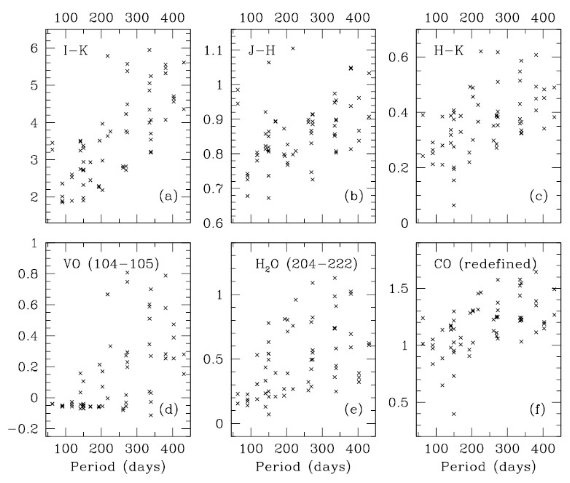 図5.O-リッチ LPV のカラー、分子指数と周期の関係。 |
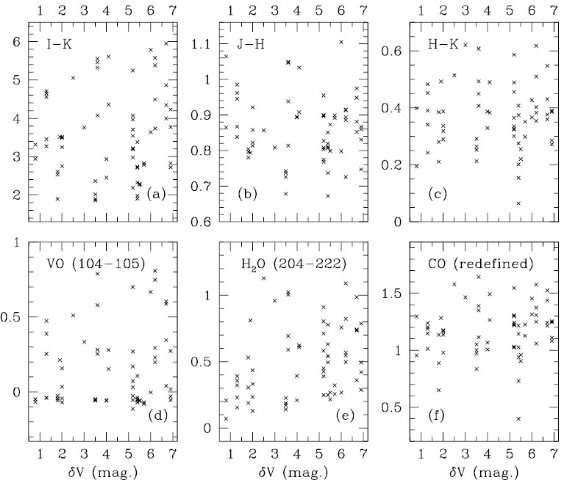 図6.O-リッチ LPV のカラー、分子指数と可視振幅の関係。 |
|
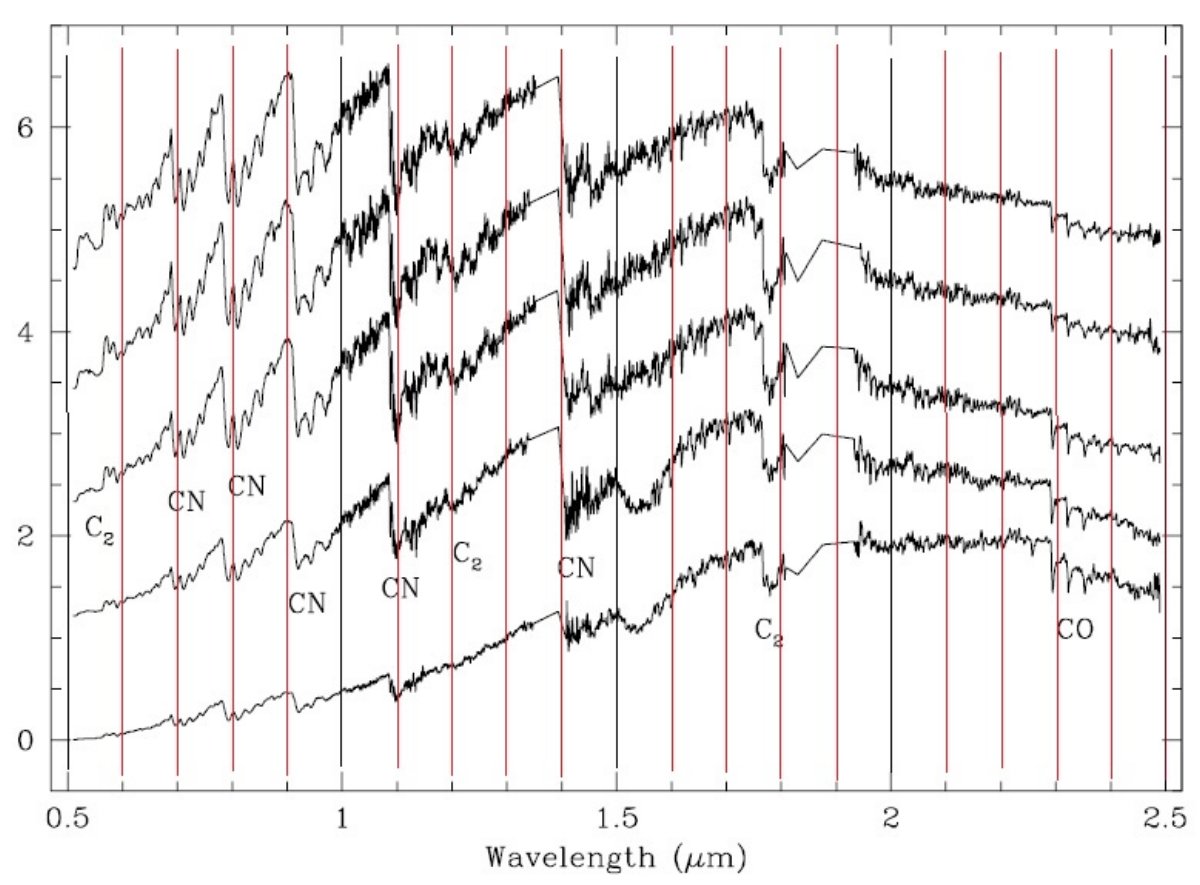
(R-J) と (R-H) は良い温度指数 Loidl e al 2001 は(R-J) と (R-H) は炭素星の良い温度指数とした。 C2 C2 は 1,768 - 1.782 μm で測り、連続光は 1.752 - 1.762 μm で 決めた。 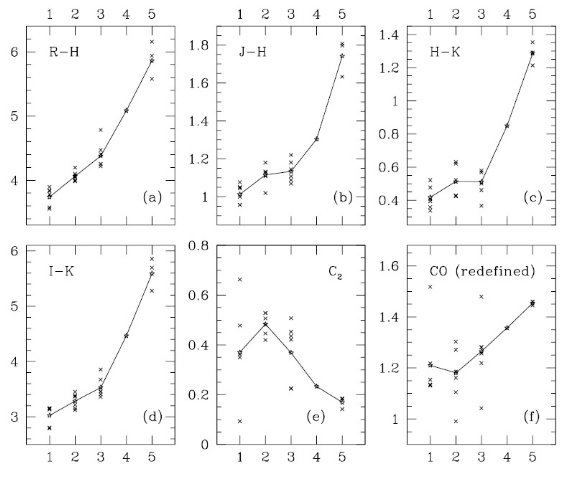 図8.(R-H) に基づいて決めたビン番号と分光測光指数の関係。 |
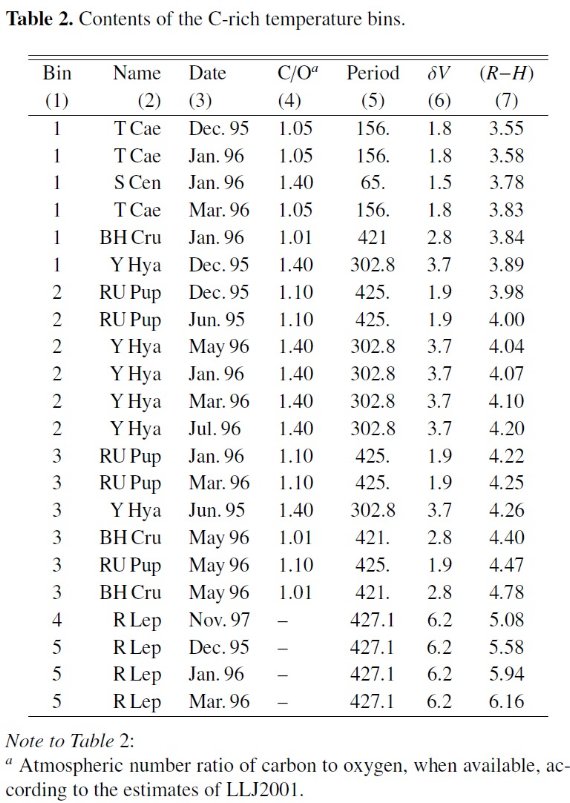 表2.炭素星の温度ビンの中身 |
|
OH/IR 星の MIR 放射は強い OH/IR 星とその C-リッチ対応天体は 上部 AGB に出現する。与えられた L で考えると、 NIR での寄与は小さいが、MIR では寄与が大きい。従って、中間 年齢種族を探すには向いている。(Bressan et al 1998) 赤化モデルの利用の薦め ダスト星の可視、近赤外放射を表現するには、この論文で示したスペクトルに赤化を かけたものを使用することを薦める。星周ダストと星間ダストは違うかも知れないが、 LW2000 データを見ると、Cardelli et al 1989 減光則を第1近似として用いても大丈 夫そうである。LW2000 は OH/IR 星スペクトルを含んでいる。図9では WX Pcs, AFGL1686 を(ビン9スペクトル+赤化)と比べた。どちらも似たような H2O, TiO, VO を含んでいる。一致はかなり良い。 星周ダストと星間ダスト この問題をさらに調べるにはより多くのデータが必要である。炭素星に対し似た手続きを 行うことも重要である。 |
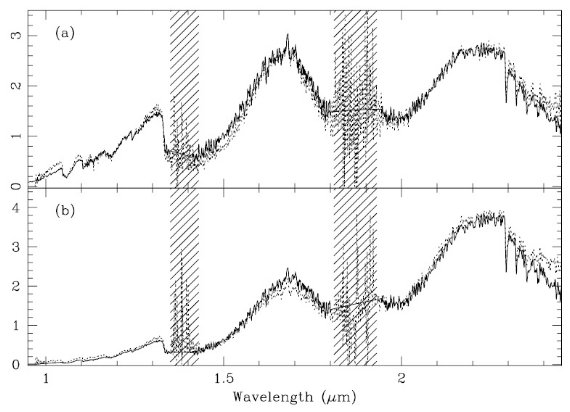 図9.上: 点線=AFGL 1686 2回観測平均。実線=(ビン9スペクトル+Av=3 の赤化) : 点線=WX Psc。実線=(ビン9スペクトル+Av=18 の赤化) |
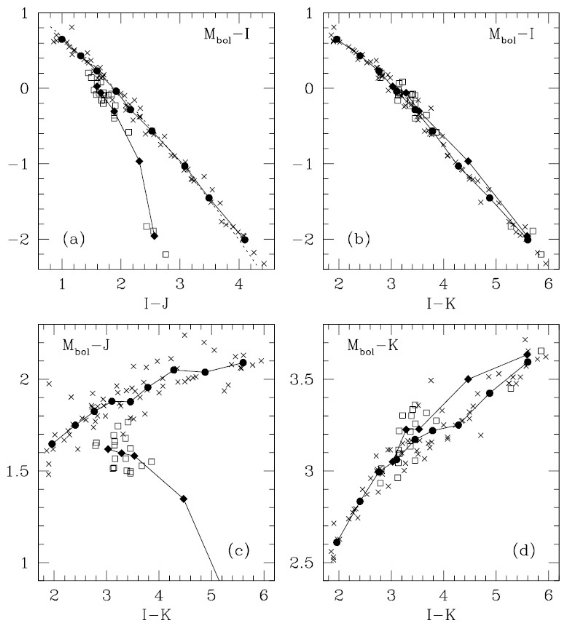 図10.輻射補正とカラーとの関係。十字= O-リッチ LPV. 四角= C-リッチ LPV. 黒印=平均スペクトルの輻射補正。 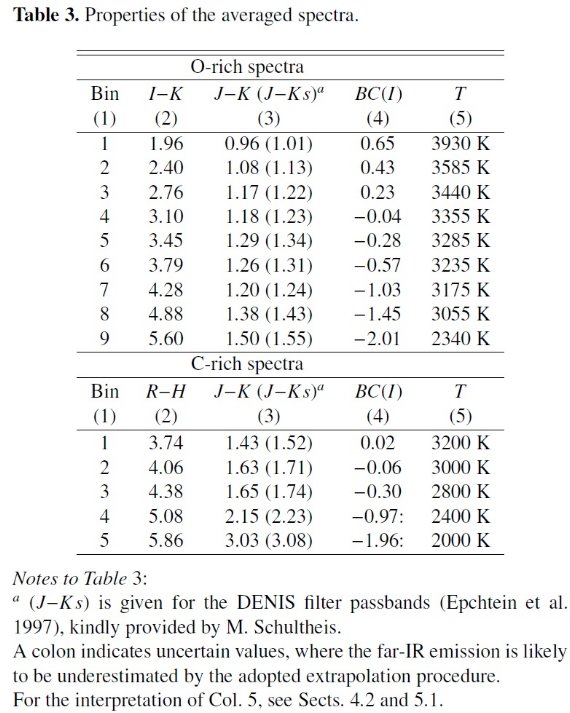 表3.平均スペクトルの性質 |
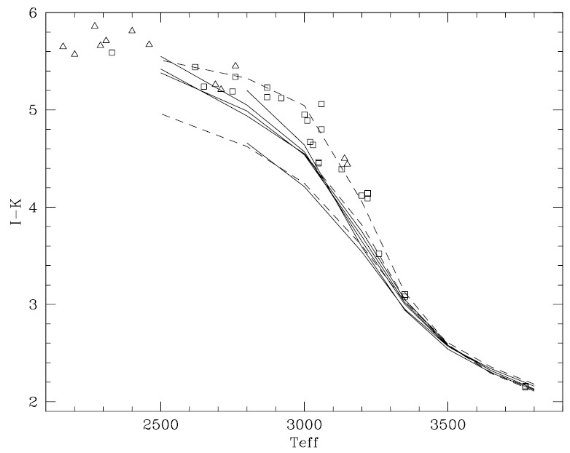 図11.モデルスペクトルによる有効温度スケール。 上破線= Bessell et al 1989 1 Mo 静的モデル。104Lo,Zo. 中破線=同上。 2×103Lo,Zo. 下破線=同上。104Lo,Zo/2. 実線=Bessell et al 1991. 4本まとまっている= Z=Zo で M=1, 1.5, 2.5, 5 Mo の AGB 軌跡。下の一本= Z=Zo/2、M=1 Mo の軌跡。 三角= Bessell et al 1996 動的モデル phase=0.5。四角=Hofmann et al 1998 動的モデル phase=0.8 - 0。 LPV の温度 図11で破線は M = 1 Mo の静的大気の系列であるが、個々星の脈動に伴う 動的モデルが 破線に沿って分布するのは興味深い。このモデル系列が表3の 平均スペクトルに対する有効温度を与えている。 ( 平均スペクトルの I-K 値に対応する、図11の上破線の Teff を表3に載せているということか。) もし、 Z を下げると、同じスペクトル(同じ I-K )に対しては下破線を使用するのでより低い 有効温度が採用される。 炭素星の有効温度 炭素星 Teff > 2600 K に対しては Loidl, Lancon, Jorgensen 2001 の (R-H) - Teff 関係を採用した。図7の平均スペクトルを用いた Teff が表3に載せてある。 最も低温の星 R Lep P=427 d は干渉計観測から Teff = 2058 K が得られている。 |
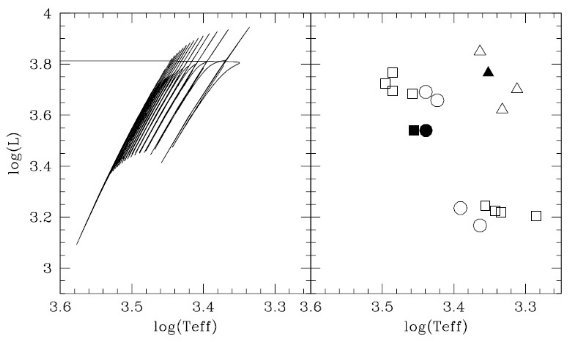 図12.(左) Minit=2Mo, Nfinal=0.6Mo の星の TP-AGB 進化。 (右) Hofman et al 1998 の 1 Mo 脈動モデル。四角=P シリーズ。 丸=M シリーズ。三角=O シリーズ。黒印=静的母星。 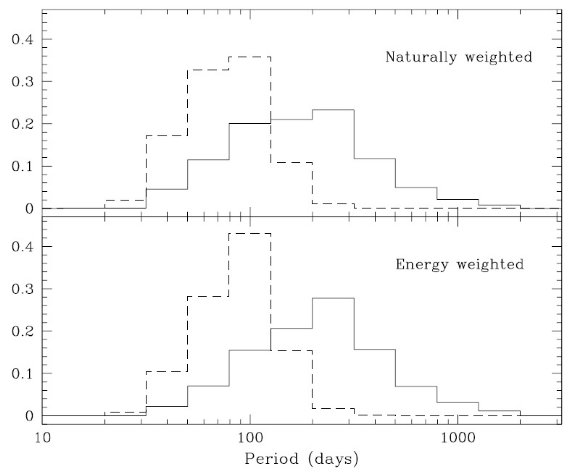 図14.Minit = 2 Mo、Z = Zo の星集団の周期分布の予想。実線=基本振動モード。 破線=第1倍音モード。 |
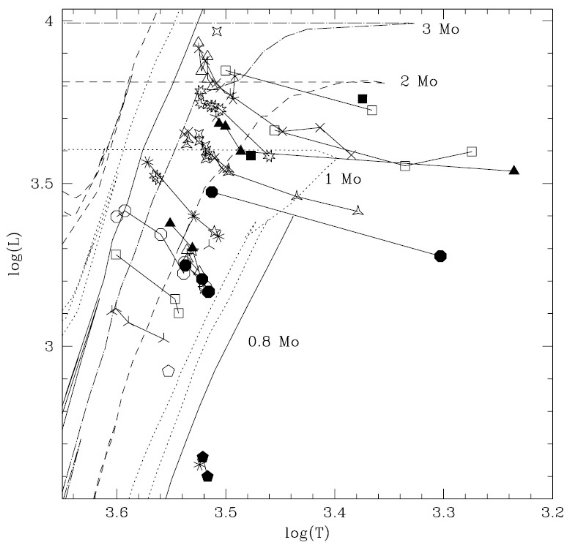 図13。 LW2000 スペクトルのモデル HR 図上の位置(定性的)。Teff は I-K から 決めた。 log L は周期と観測位相に合わせた輻射補正を用いた。 Z = Zo に対する AGB 進化経路を重ねた。 |