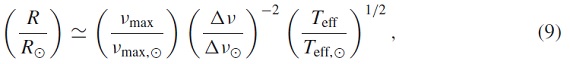Integrated Mass-Loss of Evolved Stars in M4 Using Asteroseismology

　アブストラクト　

　１．イントロダクション　

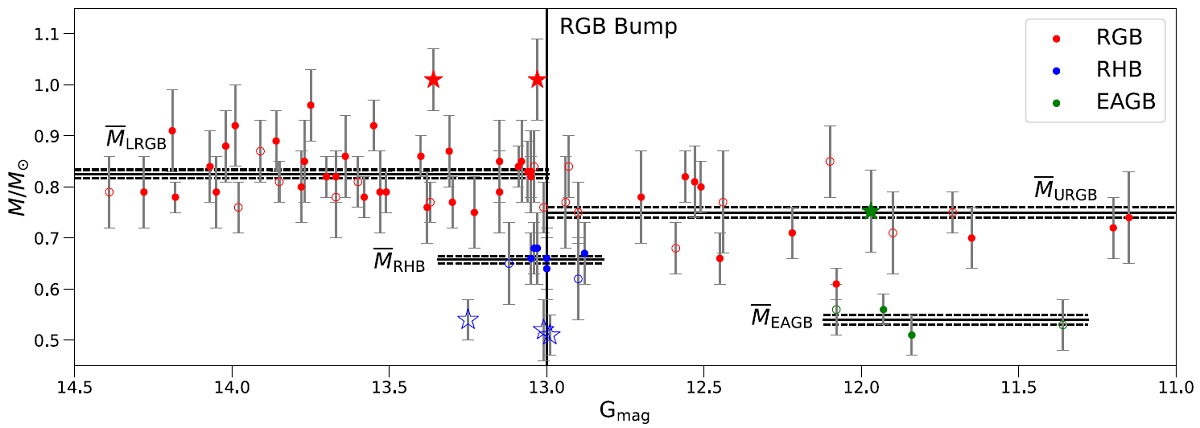
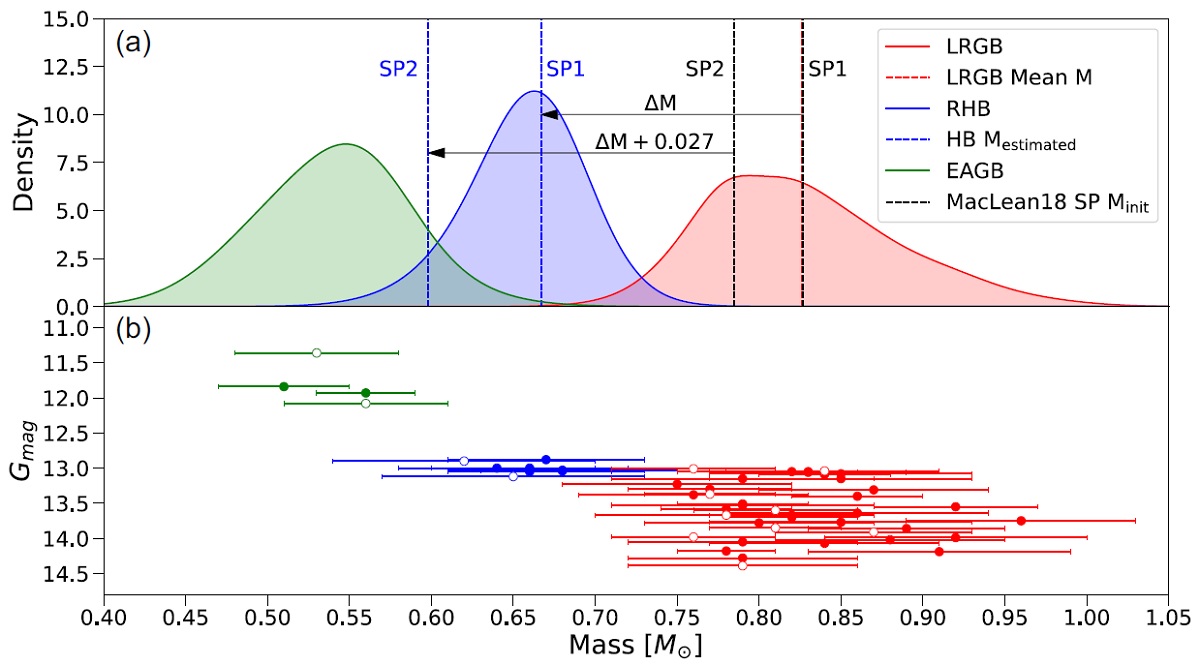
RGB マスロスモデル　 Reimers　1975 : マスロス公式 Schroder,Cuntz　2005 : Reimers　改訂版 Mullan,MacDonald (2003) ：RGB bump まではマスロス起きない。 Bharat,Kumar 2015: 同じ Meszaros,Avrett,Dupree 2009: RGB マスロス強度は期間中一定 Origlia et al 2010 : 短期に起きる Mullan,MacDonald 2019: モデル間の矛盾は機構の理解が不十分だから。 　球状星団星の累積マスロス量　 CMD フィットから、典型的な値として、 Mto=0.8 Mo, Mhb=0.6 Mo. バルマー線フィットから、Mwd=0.50-0.55 Mo 従ってマスロス量としては、 RGB 期に 0.2 Mo, AGB 期に 0.05 - 0.1 Mo である。これは、測光観測で較正した進化モデル（McDonald, Johnson, Zilstra 2011, Salaris, Cassisi,Pietrinferni 2016）で再現されている。 　球状星団 RGBs からのマスロス観測　 Origlia et al (2007), 2014：Tuc47 星周ダストの赤外測光観測　 Boyer et al 2010, McDonald et al 2011: 過大評価である　 Cohen 1976, Gratton 1983, Gratton, Pilachowski, Sneden 1984,　 Meszaros, Dupree,Szentgyorgyi 2008, Meszaros et al 2009 : Hα 輝線　 Dupree,Hartmann,Avrett 1984, Dupree 1986: 輝線ウィングは彩層起源で？

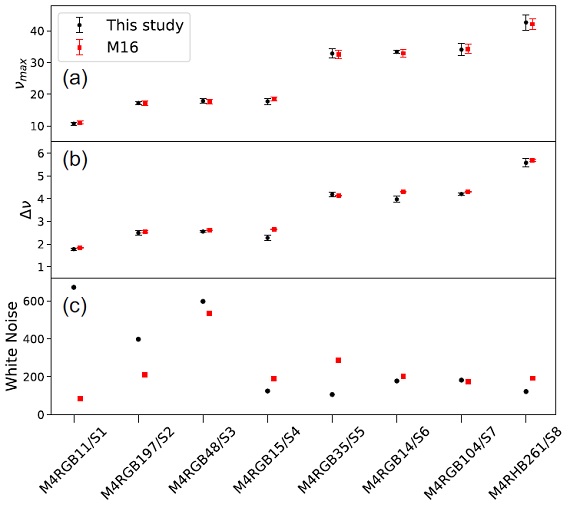
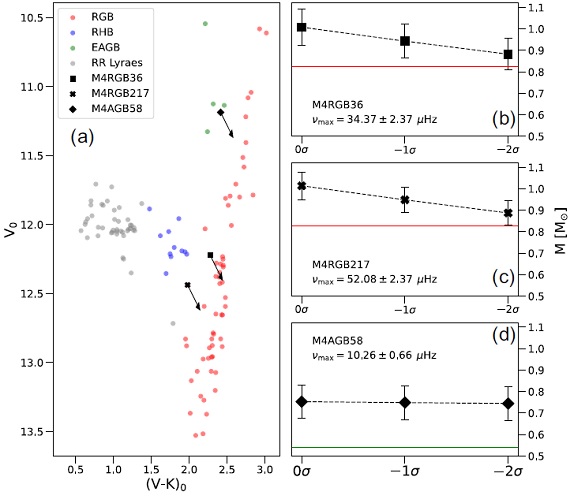
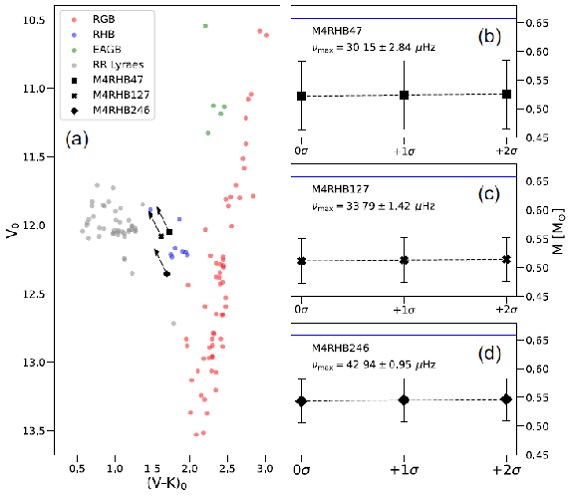
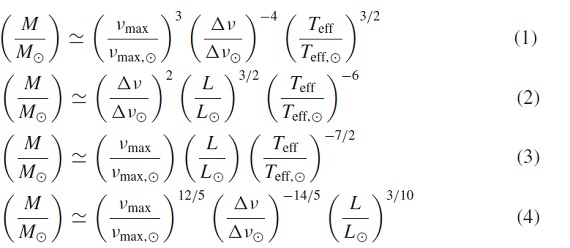
星震学質量　 ｐ−モード振動の観測で、次の量を求める。　 νmax = 振動エネルギー最大の振動数。　 Δν = 振動数間隔　 　νmax ∝ g Teff-1/2 　Δν ＆prop；⟨ρ⟩1/2 　L ∝ R2Teff4 から、 　散開星団における観測　 Miglio et al 2012, Handberg et al 2017 : NGC6791, NGC6819 Kepler 観測 　　RC 質量と RGB 平均質量との差は小さい。 　　ΔM6791=0.09±0.03 Mo, ΔM6819=-0.03±0.04 Mo. Stello et al 2016 : M67 で　RGB 質量差 = 0.02 - 0/.05 Mo. K2 観測。 散開星団の等時線フィットからも差は 0.01 Mo のオーダーである。Kramers 則 からも若い星団では RGB マスロスは小さいと思われる。一方、球状星団はRGB 寿命が長く、大きな質量差が見込める。

　２．観測　

図２．３種類基準時間 9, 5, 1.5 日に対するパワースペクトル。 灰色帯＝振動パワーの超過の外郭。 (a) M4RGB225 (b) M4RGB104. 　２．２. detrending pipeline　 　 観測間隔　 　K2 観測期間は 80 日でその間に 3856 30分間隔観測が行われた。 各ターゲットピクセルファイルは 50x50 ピクセルである。 　LightKurve　 　パイソンの LightKurve パケッジを使用した。 ステージ１：　EVEREST パイプラインのために開発されたピクセルレベル 　　　　　　　脱相関法により、各ピクセルから装置ドリフトで生じる 　　　　　　　エラーを消す。 ステージ２：　セルフフラット脱トレンド法は長期変光を除いて、平坦な 　　　　　　　光度曲線を残す。脱トレンドの際に使用する基準時間を 9 d 　　　　　　　とした。 　図２　 　ステージ２での基準時間の影響を調べるため、M4RGB225=進化の進んだRGBで、 νmax = 3 μHz と M4RGB104 = 35 μHz の２星について、 基準時間を変えて脱トレンドした結果を図２に示す。

表１．低 SNR のために太陽型振動の検出が暫定的な星のリスト。 一応得られた νmax も示した。これらの星は解析には 用いない。 　M4RGB225 の場合、パワー超過がはっきり示されたのは基準時間が 5, 9 日 の時である。元々、脱トレンド法は 6 時間の衛星回転によるノイズを減らす ために開発された。そこで、我々は長い基準時間でもノイズが効果的に消さ れるかを検証した。M4RGB104 では基準時間の変化は結果に影響していない。 　太陽型振動　 　以下の星はサンプルから外した。 (i) パワー超過が検出されなかった。BHB 星や BS 星は太陽型振動を検出する 事が不可能なので外した。 それらには G < 10 mag の明るい赤色巨星も 含まれる。それらは νmax νmax < 2 μHz となり今回の観測 では期間が足りなかった。 (ii) RR Lyr 星 (iii) 太陽型振動の検出が S/N < 5 と低い星。それらは主に RGB 下部の 暗い星である。 　Δν の問題　 　低 S/N で問題になるのは Δν の決定が困難になることである。 その場合、自己相関関数から明瞭な繰り返しパターンが消えてしまうのである。

　３．星震学量　

図４．Δν 測定の比較。赤＝Miglio et al 2016 の直接測定。 青＝Equ 5,6,7 からの結果。黒＝今回の結果。 (a) νmax. １σ で一致。(b) Δ&nu:. 2σ で 一致。(c) 白色雑音メトリック。GB11 では我々のノイズが大きい。 　pySYD パイプライン　 　νmax, Δν の測定は、観測から得た光度曲線とパワー スペクトルに pySYD パイプラインを適用して行う。これは SYD パイプライン をパイソン用に書き直したものである。pySYD は最適化ローレンツ型モデルを 用いて背景フィットとパワースぺクトルの強い平滑化を行い、νmax を評価する。Δν は自己相関関数から決める。モンテカルロ計算から 不定性が算出された。 　背景フィット　 　５４星では SNR が低いために背景フィットのエラーの評価が不安定となり、 背景フィットに失敗した。これらの星に対しては安定な線形背景モデルを使用 して超過パワー輪郭を導いた。チェックのため、SNR の高い星で線形背景モデル 空の結果をローレンツ型背景モデルからの結果と較べた。得られた全体的な星震 学パラメターに系統的な差は検出されなかった。背景フィットの例を図３に 示す。 　νmax - Δν 関係　 　νmax と Δν の間には、 Δν = ανmaxβ という関係が ある。α と β は星質量と進化段階に依存するので既存データを 用いた較正が必要である。Stello et al 2013, Vrard et al 2018, Yu et al 2018, Dreau et al 2021 からの結果を APOKASC-2 カタログで補って用いた。 その結果が次の式である。

図５．(a) νmax 評価エラーのヒストグラム。 黒縦実線＝RGB/EAGB の K2GAP 結果のメディアン。黒縦一点鎖線＝ＲHB. 図内表示 μ = 我々の結果のメディアン。 (b) Δν エラーの比較。 　図４＝直接測定結果との比較　 　図４に Miglio et al 2016 の直接測定結果との比較を示す。 今回の観測は白色ノイズが高いことが判る。しかし、それは結果にあまり 影響していない。 　図５＝Ｋ２ＧAP との比較 　図５にはエラー分布を K2GAP = K2 Galactic Archaeology Program と 較べた。今回のエラーが大きいことが判る。 　表２＝各星の結果　 　表２には M4 星の結果の例を載せた。

　４．星の物理量　

４．１．有効温度と減光　 　異常減光則　 　M4 は　Sco-Oph 分子雲複合体の背後にあり、相当な赤化を被っている。 微分赤化の効果も無視できない。Dixon, Longmore 1993, Ivans et al 1999 によると、Ｍ４ 方向の減光則には非正常ダストタイプの影響がある。 Hendricks et al 2012 は R = 3.62±0.07 とした。 　各星毎の減光　 　Hendricks et al 2012 の M4 微分減光マップを用いて個々星の減光を決めた。 このマップの減光量は平均 E(B-V) = 0.37 で、散らばり σ = 0.02 である。 ただ、サンプル星の 15 % はマップの外にある。それらの星にはマップ内星の 平均減光量 E(B-V)=0.36 を適用した。 　測光温度　 　Campbell et al 2007 は進化した星では V-K から決め た温度が信頼度が高いと述べている。そこで、 (a) J,H, K 等級（２MASS)、B,V 等級 (Mochejska et al 2002, Momany et al 2002) から　（V-K), E(B-V) を得る。 (b) E(V-K) - E(B-V) 関係を Fitzpatrick, Massa (2007) から採る。 (c) 巨星の (V-K)o - Teff 関係は Gonzalez Hernandez, Bonifacio 2009. から [Fe/H] = -1 での測光温度を定めた。エラーの最大原因は赤化補正である。

図６．星毎の Teff(分光)-Teff（測光）.実線＝一致ライン。 破線＝平均値 80 K. 　分光温度　 　MacLean18 の分光サンプルには、今回と重なる 39 RGBs と 3 EAGBs が 含まれる。図６を見ると、分光温度と測光温度との間に平均 81 K の差がある。 そこで、分光データの無い星の測光温度には 81 K を足して使用する。こうして 決めた温度の不定性は、分光温度の誤差と二種温度間の温度差散らばりの自乗和 から 108 K と見積もられる。表２に温度を載せた。

４．２．光度　 　光度は赤化補正等級 Vo, 輻射補正 BC, から以下の式で決められる。 　log(L/Lo) = -0.4[Vo - (m-M)o + BC - Mbol,o] Mbol,o = 4.74 ±0.13 は Cox 2000, Torres 2010, Mamajek et al 2015 から採った。(m-M)o = 11.34±0.02 は Baumgardt,Vasiliev 2021 から。 光度 　L は表２に載せてある。 　４．３．半径　 　Rseis の計算　 　半径 Rseis の計算には下の式を用いる。 太陽の値、νmax,o = 3090±30 μHz と Δνo = 135.1±0.1 μHz は Huber et al 2011 から、Teff,o = 5772 ±0.8 K は Mamajek et al 2015 から採った。 図７には．Rseis/Rphot の分布を示す。中間値残差＝２％。散布度＝ 20 % で ある。７星で 2 σ 以上離れているのは Δν のような星震学的 パラメターの決定にエラーがあるためと考えられる。

図７．R(星震)/R(黒体)の分布。中間値残差＝２％。散布度＝ 20 % である。 　Gaia 測光半径　 　Zinn et al 2023 は Gaia 視差を用いて星震学物理量の検証を行った。 彼らの結果では R < 30 Ro の星に対し、 Rseis と Rphot は 2 % 以内の 誤差で一致する。これは今回の結果と合致する。

　５．質量　

　５．１．星震学質量とその平均値　

Mseis の計算　 　式 (1) - (4) に得られた νmax, Δν, L, Teff を 入れて各星の質量を決めた。Mullan, MacDonald 2003, 2019, Bharat Kumar et al 2015 はマスロス開始は RGB バンプ光度付近ではないかと推測している。 我々の目的は、初期質量 Mto と水平枝質量 Mhb との間の質量差の決定である。 そこで、 RGB を　RGB バンプの光度で URGB と LRGB に二分した。バンプ等級は V = 13.6 mag (G=13 mag) とした。Song et al 2018. 　Δν 補正　 　振動の一般的関係 Δν ∝ ⟨ ρ⟩1/2 からのズレが知られているが、それは質量推定 に系統的な差を生じる。この差の原因は内部構造に依るらしく、 通常は Δν にモデルから得られる補正値を施す。我々は asfgrid (Sharma et al 2016) からの補正を使用した。注意しておくが、我々の サンプル星の 44 % はこのモデルグリッドの質量限界より下にある。この ため、それらの星の Δν への補正が過小である可能性がある。 また、このモデルグリッドは EAGBs を扱っていない。 EAGBs に対しては ＲGB と同じ補正を使用した。 　平均質量　 　表３と表８には上の補正を加えた場合と加えなかった場合の LRGB, UERGB, RHB，EAGB の平均質量を示す。暫定検出（MD)星も加えたが、外すと RHB, EAGB 星は少し小さくなる。 　式（３）が最も正確？　 　各関係式からの平均質量間の不定性を平均質量の不定性と考える。表３を 見ると、式（３）からの不定性が最も小さい。また、式（３）質量は M4 モデルから予想される質量 McDonald, Zijlstra 2015, MacLean 2018 に最も近い。更に Miglio et al (2016) が見出したRGB 最終質量 0.84 Mo は 式（３）からの平均質量 0.83±0.01 Mo に近い。これらから式（３） は最も正確な値を与えると想像される。 　今後は式（３）だけを使う　 　Δν 補正を行った後も式 (1), (2),(4) からの質量不定性は依然と して大きい。第３章では、SNR 測光エラーが大きくて Δν の信頼度が低い問題が指摘されていた。また asfgrid の質量範囲がサンプル 星の多くをカバーしていないために δν 補正が過小である点も問題である。 これらを考えて、特に Δν に依存しないという利点を評価して、この先 では式（３）質量のみを扱うことにする。

図８．星震学質量を計算する４つの式から決まった進化段階ごとの平均質量の 比較。横実線＝６．１．節のモデル質量。色の違いは採用したレイマーズ式 の係数の違いを示す。RGB の場合、実線は進化モデルの初期質量となるので 一本である。星数 N の添数字は採用した式の番号。式３では外れ星を除いた のでNが他より小さい。 　図９＝個々星質量　 　図９では式（３）で決めた個々星の質量を示す。外れ位置に６星＝２超過 質量 RGBs + 1 超過質量 EAGBs + 3不足質量 RHBs ある。それらは平均質量 の計算に含めない。最終的な平均質量は 0.826±0.008 Mo (LRGB), 0.658±0.006 Mo (LRGB), 0.54±0.01 Mo (RFB) である。 　Miglia et al 2016 との比較　 Miglio et al (2016) は 0.84±0.10 Mo(RGB), 0.61 Mo (RHB) である。 しかし、彼らの RHB 星は一つだけである。

　５．２．マスロス　

　５．３．はずれ質量星　

図１０．(a) 赤化補正 CMD. 黒印＝超過質量星。矢印＝減光を 2 σ 減ら した時の変化。(b), (c), (d) 減光を 1 σ, 2 σ 減らした時の 質量変化。水平直線＝進化モデルが与える質量。 　５．３．１．超過質量星　 　減光補正の修正 　 　M4RGB36 = 1.01 Mo, M4RGB217 = 1.01 Mo, M4AGB58 = 0.75 Mo で大き過ぎる。 それらは H12 減光マップ範囲内にあり、 E(B-V) = 0.37 mag である。減光の 細かい変化で個々星の減光が変わっている可能性もある。図１０には 2 σ の変化を与えた場合を示す。 σ = 0.02 mag である。 　M4RGB36, M4RGB217　 　この二星は分光温度が与えられている。それらは測光温度との差が大きい 事が判った。これは赤化補正が大き過ぎたことを支持する。2 σ 修正 の結果質量は 0.06 - 0.07 Mo 低下する。これは LRGB 質量の 1.5 σ 範囲に収まる。 　M4AGB58　 　質量は平均値の 40 % 増しである。赤化補正を直すと EAGB と URGB の 中間に来る。分光温度が欲しい。

図１１．図１０と同じだが、不足質量星。こちらは減光量を 1, 2 σ 増加させた場合の変化を示す。 　５．３．２．不足質量星　 　M4RHB47, M4RHB127, M4RHB246　 　M4RHB47 = 0.52 Mo, M4RHB127 = 0.51 Mo, M4RHB246 = 0.54 Mo である。 モデルでは M(RHB) = 0.6 Mo であり、不足している。これら３星は暫定検出 星である。従って星震学パラメターの精度は低い。より高精度の測光が第１に 必要である。 　変更補正の修正　 　減光補正の修正の効果を調べるため、　図１１では 1, 2 σ 減光を 増加させた。測光温度だけでなく分光温度が必要である。

　６．議論　

　６．１．モデルへの影響　

　６．２．複種族：双モード？　

　６．３．EAGB 質量　

　６．４．非標準進化？　

　７．結論