Synthetic Photometry for Carbon-Rich Giants IV. An Extensive Grid of Dynamic Atmosphere and Wind Models

　アブストラクト　

　１．イントロダクション　

　２．動力学モデル　

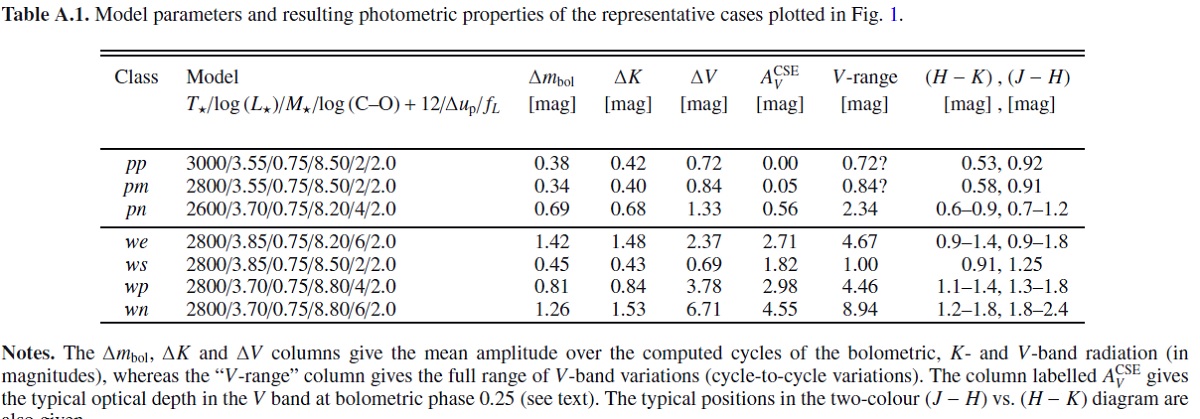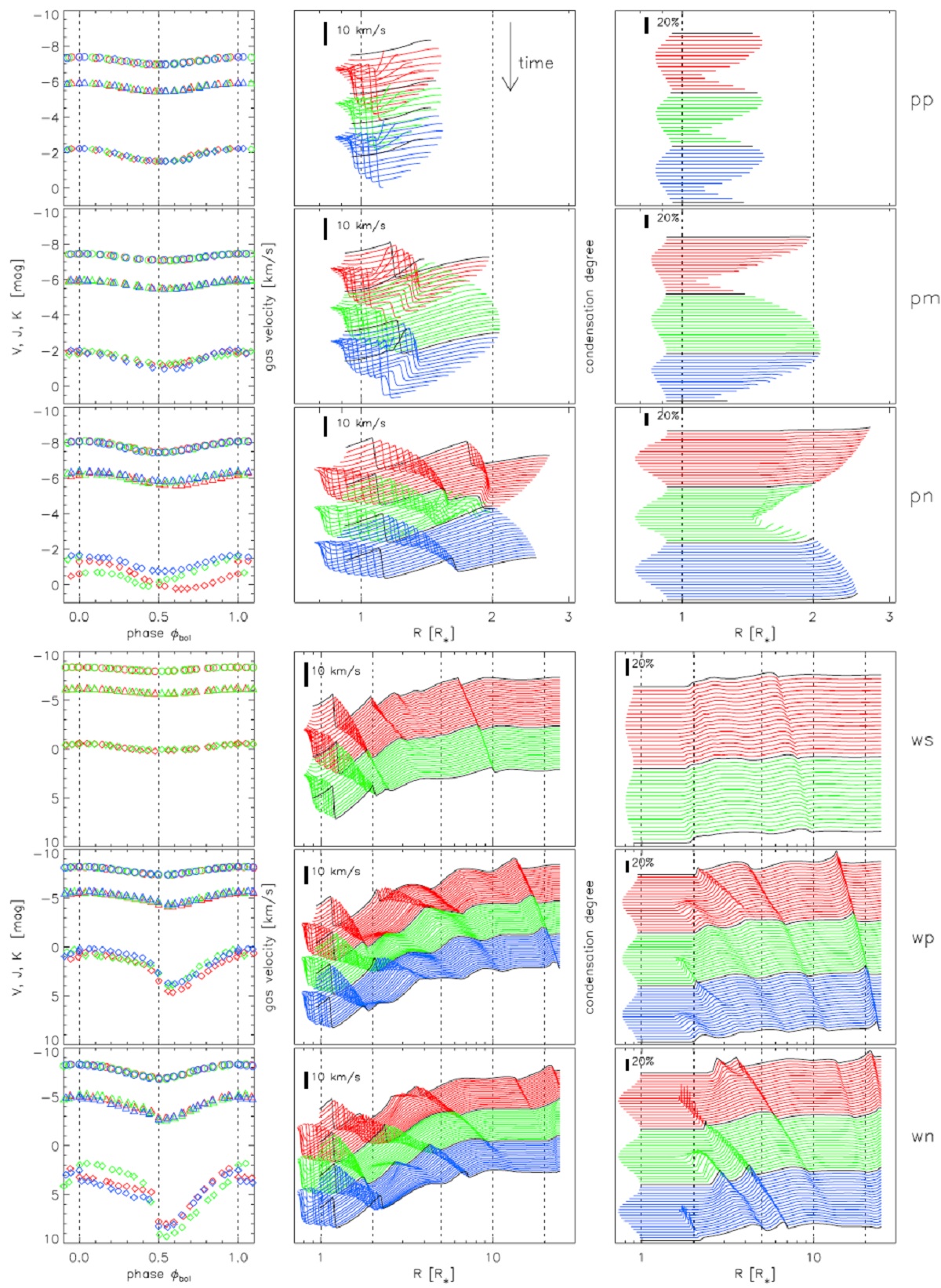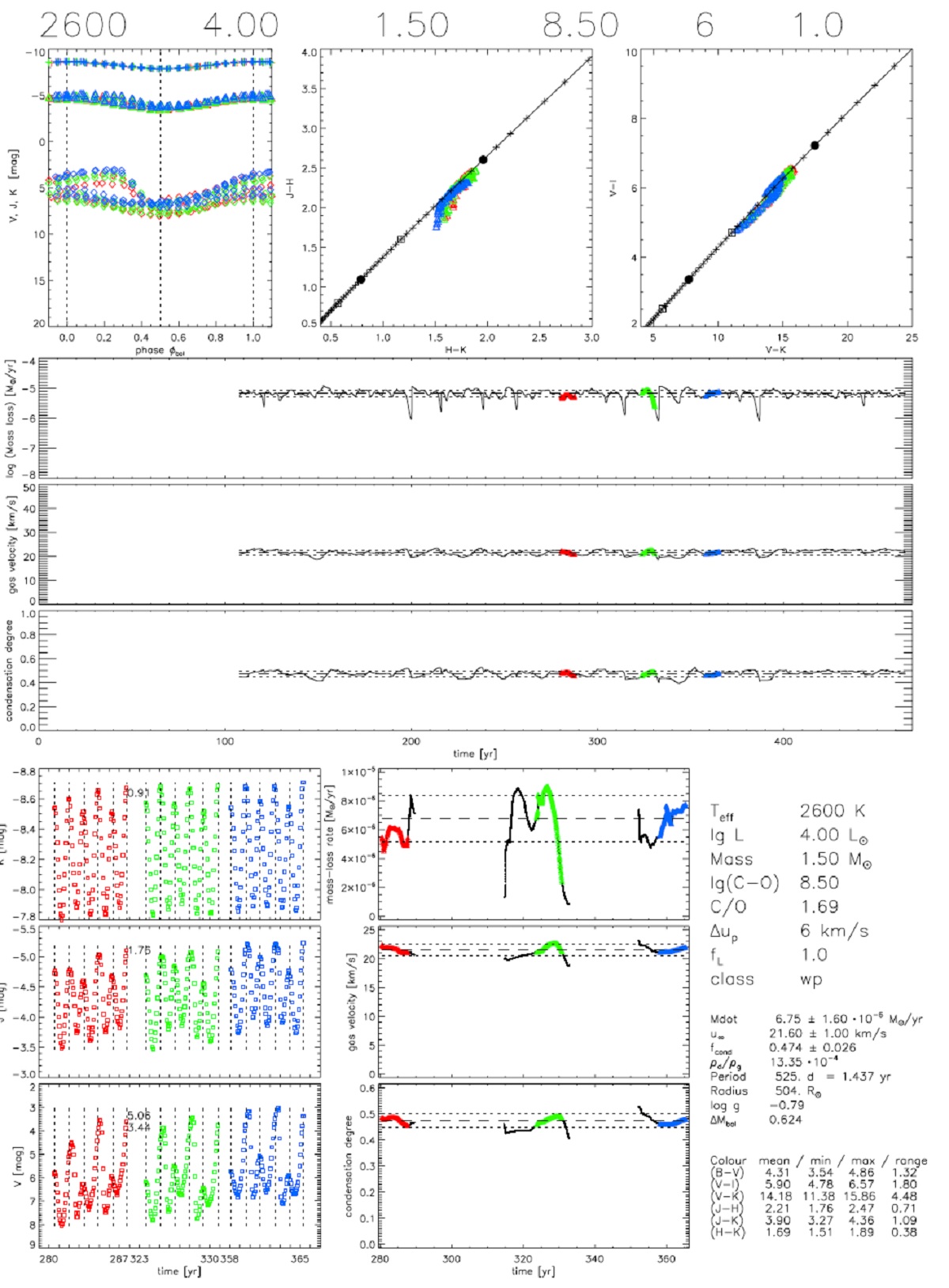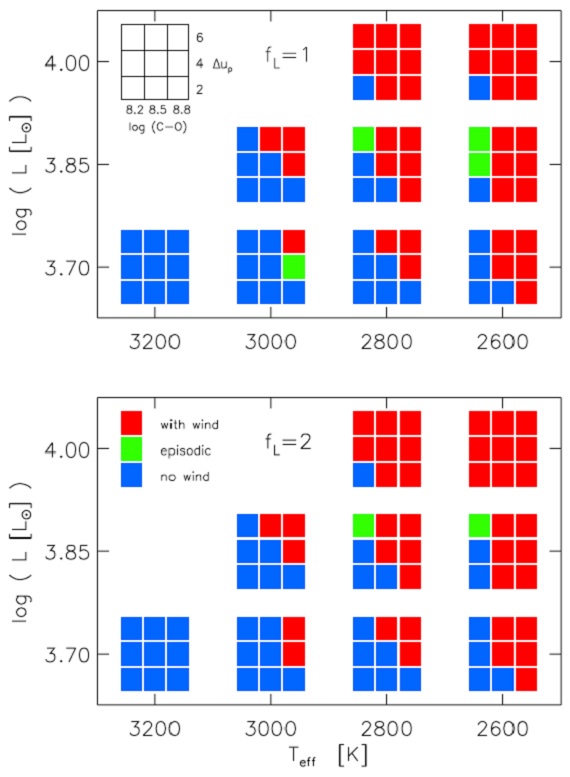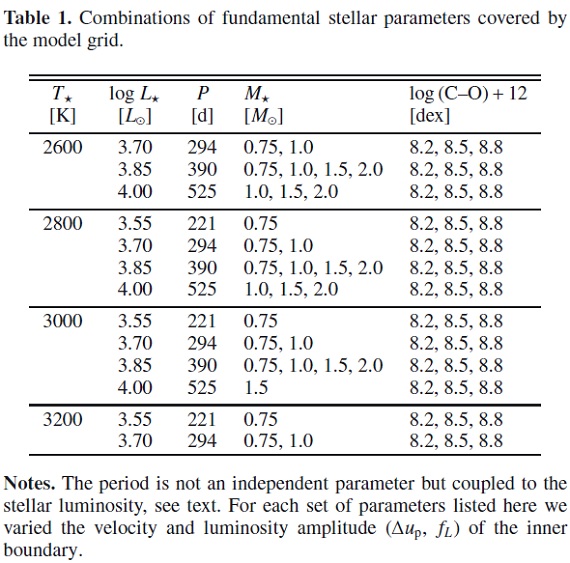
表１．モデルグリッドのパラメターの組み合わせ。 　２．１．動力学大気と星風のモデル　 　動力学モデル　 　動力学モデルは Hofner, Gautschy-Loidl, Aringer, Jorgenson (2003), Mattsson et al. 2010 を使う。このモデルは動力学面では脈動が原因の衝撃波 とダスト駆動星風を扱える。各モデルは数百周期を計算している。 モデルの内側境界は速度が正弦曲線型に変化するという条件を与えられる。 これはピストンモデルと呼ばれる。それに伴う光度変化は別に与えられる。 　脈動の効果　 　脈動は大きなスケールでは衝撃波を産み出し、静止大気とは全く異なる変動 大気構造を生み出す。微細スケールではダスト形成が平衡状態とは離れた過程 で進行する。それは 106 - 109 個の原子が一個の ダスト粒子に集結するグレイン成長の時間スケールが動力学時間スケールと 近い (Gustafsson, Hofner 2003) からである。さらに微細なレベルでは、 Cherchneff 2006, 2012 は衝撃波により分子組成が平衡から離れた状態に 導くとした。

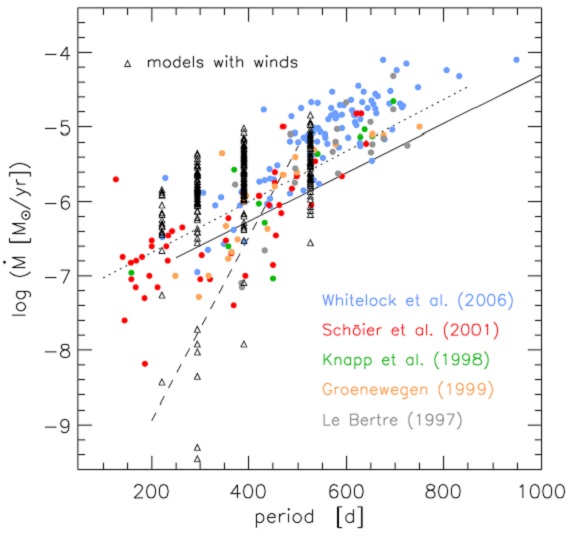
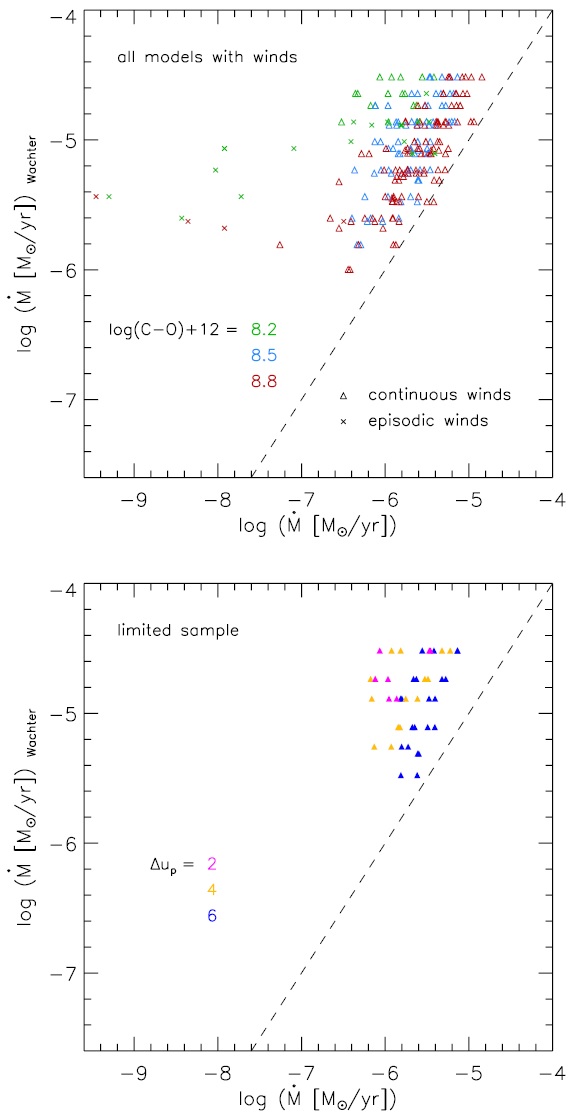
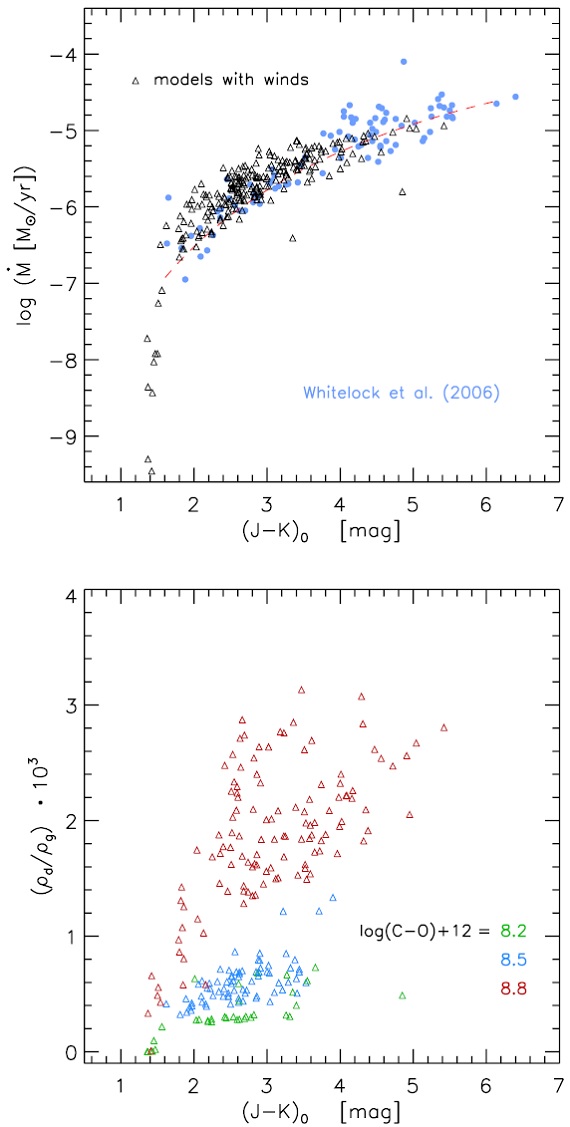
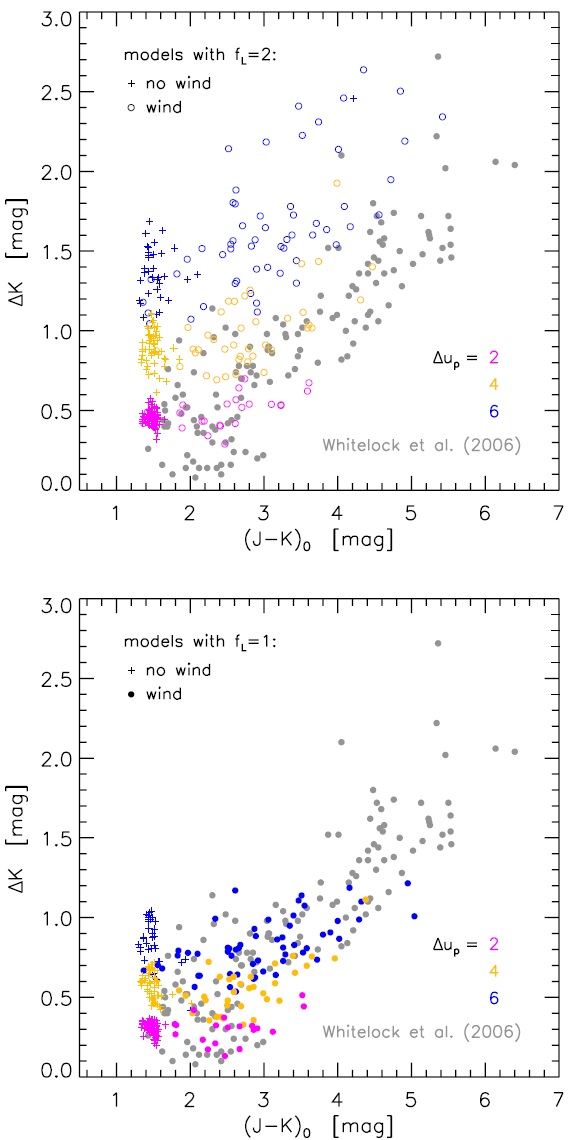
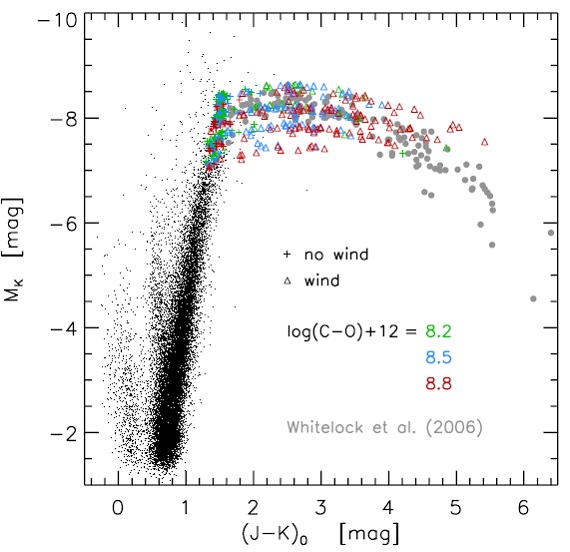
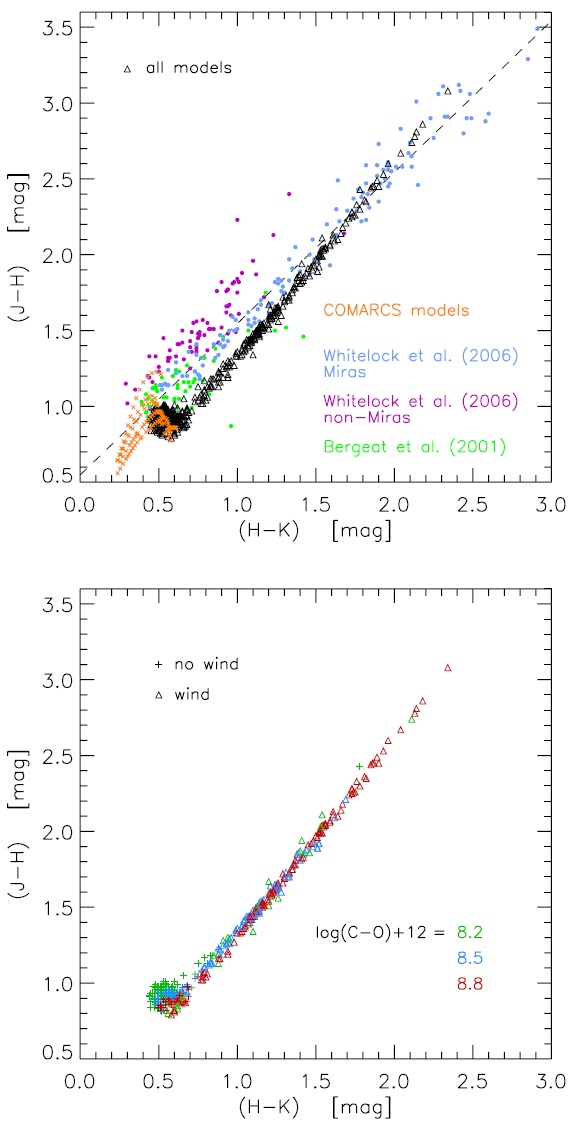
表２．炭素超過指数 = log(C-O)+12 と C/O の関係。O の組成は log(NO/NH)+12 = 8.66 である。 　２．２．モデルグリッドのパラメター　 　使用パラメター　 　Mattsson10 では大規模なパラメター空間にまたがるモデル計算がなされた。 この論文で用いるのはそのサブサンプルで、 Bertelli et al 2008, Marigo et al. 2008 による AGB 経路に沿ったパラメターを使用する。それらを 表１に示す。 　元素組成　 　C 以外の元素組成は太陽組成に従う。その値 は log NH = 12 で規格化されている。 Asplund et al 2005 の太陽組成は X/Y/Z = 0.73/0.25/0.015-0.020 で与え られる。Z の変化は C 組成の変化に伴うものである。星パラメターの各組に 対して、炭素超過を log(C-O)+12 = 8.2, 8.5, 8.8 で、ピストン速度振幅 Δup = 2, 4, 6 km/s で与えた。炭素超過と通常用いられる C/O との関係は表２に与えられる。 脈動周期は Feast et al. (1989) の光度周期関係から定められ、表１に示されている。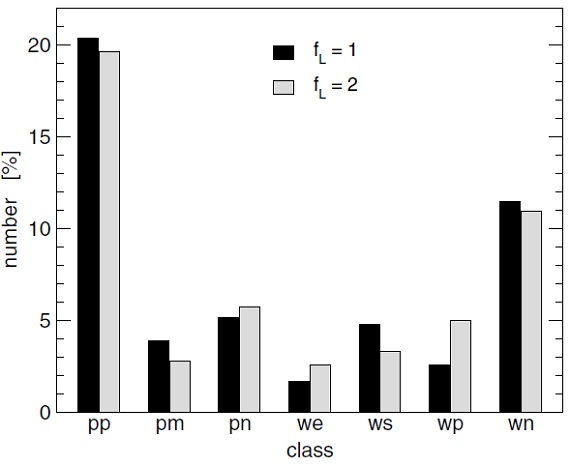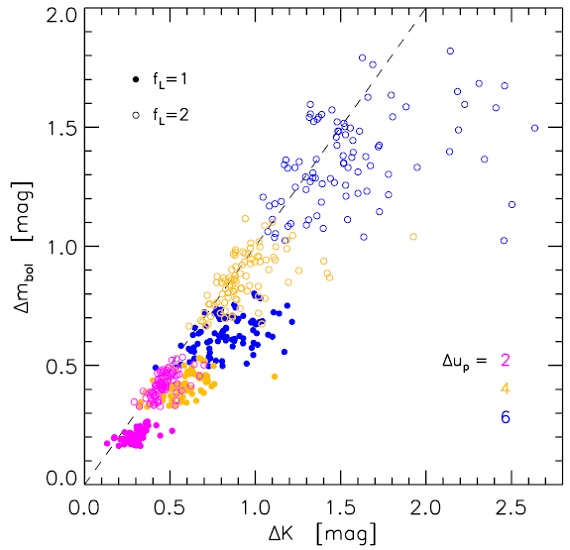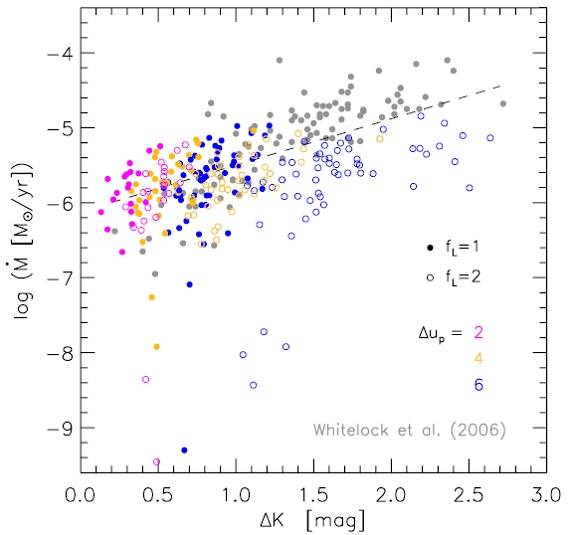 　半径、光度変化　 　速度、そして半径の変化は正弦曲線型で与えた。速度変化は直ぐに衝撃波と なり、その強さは速度振幅で決まるので、変化の関数形は重要でない。 内部モデルがないので、境界での光度変化は半径変化と同期し、光度変化の 振幅は半径振幅に相関すると仮定する。 Hofner, Gautschy-Loidl, Aringer, Jorgenson (2003) では、内側境界でフラックス一定、つまり光度 L は 半径の二乗に比例すると 仮定した。しかし、この仮定では光度変化が小さくなり過ぎると分かった。 そこで光度振幅が Hofner03 と同じモデルは光度調整ファクター fL = 1, fL = 2 の時は光度振幅がその２倍とする。 　モデル数　 　こうして総計 540 の異なるパラメターセットを持つモデルを計算した。 内 229 は星風を産み出し、 311 は星風が起きなかった。

　図１．分類群ごとのモデル例　

　３．力学的、測光的な振る舞い　

３．２．パラメターの効果　 図２．１Mo モデルでの力学的振る舞いを HR 図上に示す。 　 　ピストン速度　 　ピストン速度が　Δu = 0 - 2 - 6 lm/s と変化すると、外側大気の 到達高度も変化する。落下ガスは次の脈動で上昇中のガスト出会う。 それがどこで起きるかにより、その後の振る舞いは変わる。 a. 外側に向かうガスが薄い場合、pp, pm, pn クラスになる。 b. ws クラスでは、炭素凝結度は同一距離での違いは小さい。 c. wp クラス：各周期である距離でのダスト量は同じ。 d. wn クラス：ダスト量は時間空間で変動。

図３．二つの fL に対するモデルの分類クラス分布。 　 　炭素超過　 　同じ星パラメター、M. L, Teff に対し、炭素超過 log(C-O)+12 が 8.2 - 8.5 - 8.8 と変化するにつれ、ダスト/ガス 比が大きくなる。 炭素超過が大きいほど星風速度は大きくなり、星風は発生しやすくなる。 　M, L, Teff　 (i) Teff が低いほどダスト形成に有利。 (ii) L が高く、 M が低いと（輻射加速/重力）比が強くなる。その様子を 図２に示した。 　fL = 光度調整ファクター　 　fL = 光度調整ファクター＝内側境界での光度振幅をフラックス 一定モデルに比べて fL 倍にした。 図２には fL = 1 と 2 の場合について示す。大体は似た傾向。

　４．モデルグリッドの全般的傾向　

図４．マスロス率と星風速度の関係。上：三角＝定常星風モデル。バツ＝episodic マスロスモデル。その他は観測結果。 下：fL = 1（赤丸） と 2（白赤丸） の場合を点線でつないだ。 　４．１．星風の性質　 　低炭素超過モデル　 　図４上にマスロス率と星風速度の関係をモデル、観測で示す。図４下には 炭素超過と光度振幅の影響を示す。一般にはモデル点と観測点の重なりは良い。 しかし、例外がある：モデルで非常に低速度なのにかなりマスロスが高い。そ れらは log(C-O)+12 = 8.2 に対応する。恐らくオパシティ計算で小粒子極限 近似を使ったためであろう。 　低マスロス　 　図４では低マスロスのモデル点が不足している。また、炭素超過が 8.8 と 高いモデルでは星風速度が観測にないほど高くなる例がある。そのように高い 炭素超過が実現される例は少ないことを意味するのであろう。

図５．上：最終速度と α の関係。下：最終速度とダスト/ガス比の関係。 　fL 　 　図４下では fL = 1 と 2 の場合を較べた。 　図５上：alpha;　 　α = (ρd/ρg)(Ls/Ms) は輻射加速度 と重力加速度の比に比例する。 図５には星風速度と α の関係をプロットした。 　図５下：(ρd/ρg)　 　(ρd/ρg) の効果を他のパラメターから 分離するため、図５下を作った。

図６．黒三角＝変光周期とモデルマスロス率との関係。色丸＝観測。 破線＝ Vassiliadis, Wood (1993) のモデル。黒実線＝Groenewegen98 の C-ミラマスロス。 点線＝De Beck et al 2010 の CO 観測結果からの関係。 　図６＝周期・マスロス関係　 　図６には変光周期とモデルマスロス率との関係をプロットした。 我々のモデル計算の結果は、観測から決めた Groenewegen98, De Beck et al 2010 とよく一致する。Vassiliadis, Wood (1993)　のモデルは勾配が急すぎる。 　図７＝今回のモデルと Watcher02 式との比較。　 　図７には今回のモデルと Watcher et al 2002 の古いダスト駆動星風モデル によるマスロスを比較した。今回のマスロスは系統的に古いモデルより低い。 両者の大きな違いはガスオパシティと輻射場の取り扱いである。古い扱いでは 輻射伝達は灰色近似で解かれ、ガスオパシティも一定にされた。これが大気の 密度-温度関係に影響する。Watcher et al 2002 では低いオパシティ値が選ばれ、 その結果ある温度に対しては高目の密度を産み出した。それが大きなマスロス となったのである。なぜ我々が今回のぐり度に対してマスロス公式を与えないか の理由は Mattsson et al 2010 を見よ、

図７．今回のモデルと Watcher et al 2002 式とのマスロス比較。 上：

　４．２．測光的性質　

図８．グリッドモデルの 輻射等級の振幅 Δmbol と K 等級 振幅 ΔK 関係。破線は 1対1 関係。 　K 等級は光度の良い指標　 　K バンドではダストによる減光と放射がほぼ釣り合うので、K 等級は光度 の良い指標になる。それが変光巾にも当てはまることが図８を見ると分かる。 　J-K の意味　 　それに対して J-K はダスト減光の影響をより強く受ける。このため J-K カ ラーはダスト減光の測定に重要である。

図９．グリッドモデルの K 等級振幅 ΔK とマスロス率の関係。 　炭素星測光データ　 　モデルとの比較には Whitelock, Feast, Marang, Groenewegen (2006) による炭素星赤外モニターのデータを使う。 　図９ = マスロス率と K 振幅　 　図９にはマスロス率と K 振幅の関係を示す。灰色丸が観測点である。 (i) 観測された高マスロス (> 10-5 Mo/yr) の星に 対応モデルがない。 (ii) 与えられた ΔK に対応する dM/dt の広がりが大きい。

図１０．上：　マスロス率と J-K カラーの関係。青丸＝ Whitelock, Feast, Marang, Groenewegen (2006) の観測データ。破線＝Gullieuszk et al 2012 の近似。 下：モデルのダスト/ガス比と J-K カラーの関係。 　一致は本当？　 　図１０．上にマスロス率と J-K カラーの関係を観測とモデルの双方で示す。 モデル点が観測点の領域をほぼ覆っていることが判る。マスロス率と J-K カ ラーの明白な相関は J-K カラーがダスト外層の光学的厚みの指標となること を意味するようだ。しかし、観測結果の方はかなり高い一定の ガス/ダスト比を仮定しており、図１０下とは明らかに違うなど、よく見ると 大分差が生じてくる。他にも観測とモデルの間に差があって、うまく補い合って 最終的に良いい一致になったらしい。

図１１．ΔK - (J-K) 関係。灰色丸＝ Whitelock, Feast, Marang, Groenewegen (2006) データ。 上： fL = 2 モデル。下： fL = 1 モデル。 　動力学モデルの結果と較べるのが最良　 　観測からマスロス率を出す際の不定性を避ける方法は、観測で直接決まる量 を動力学モデルの結果と較べることである。比較的容易に得られる量として ΔK がある。図１１には ΔK を (J-K) の関数として示した。 ΔK は光度変化の指標となり、fL と Δup の双方が光度変化に影響するので、fL = 1 と 2 で図を上と下に 分け、Δup で色分けした。図から、fL = 2 で ピストン振幅が大きいモデルは観測に合わないこと、ΔK が ピストン振 幅に強く依存することが判る。またモデルでは J-K = 1.7 が星風ナシとアリ の境界をなすことも分かる。

図１２．J-K 色等級図。 黒点＝2MASS。灰色丸＝ Whitelock, Feast, Marang, Groenewegen (2006) 三角＝モデル。色分けは (C-O) 量。 　低質量モデルは観測に合わない　 　図１２を見ると、低質量、低光度で、大きな(C-O) 超過とピストン速度により 星風を起こしたモデルには観測点が対応しないことが判る。これらのモデルは 図６でも観測点から外れていた。 　図１３＝ NIR 二色図　 　図１３の NIR 二色図では、モデルと観測の一致は一般に良い。星風ナシモデ ルは、(J-H) が青過ぎ、(H-K) が赤過ぎる。 (星風ナシは J-K < 1.7 部分のこと？ それより上の黒三角は星風ありモデル？全然合ってないけど。 ) 面白いのは静止大気の COMARCS モデルが (H-K, J-H) = (0.4, 1.1) 付近に 集中することである。

図１３．（Ｊ-Ｈ）-（Ｈ-Ｋ） 二色図。上：モデルと Whitelock, Feast, Marang, Groenewegen (2006) 観測点。 下：星風モデルと低(C-O)のCOMARCS 静止大気モデル。

　５．まとめ