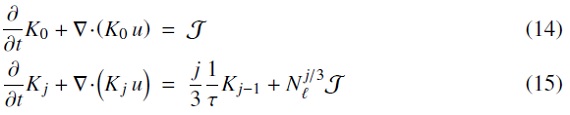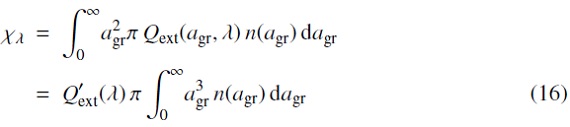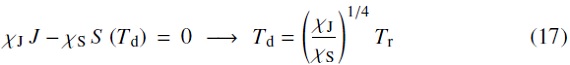Dynamic Model Atmospheres of AGB Stars
III. Effects of Frequency-Dependent Radiative Transfer

　アブストラクト　

　２．モデル　

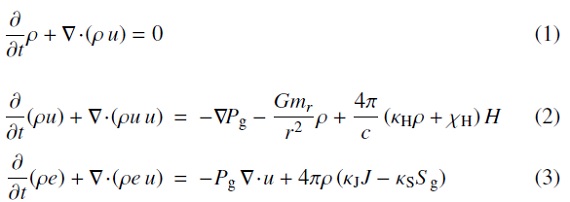
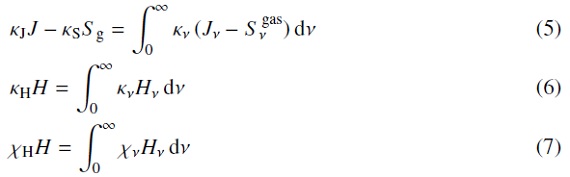
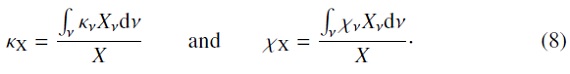
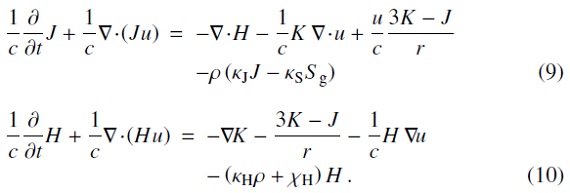
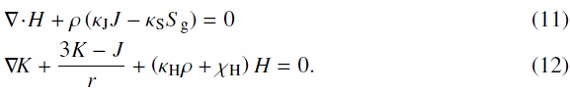
２．１．基礎方程式　 　２．１．１．輻射方程式　 　ガス　 　 　 ガスト輻射場とガスの間の運動量とエネルギー交換式に現れる項は、 　 ここに、　X は J, H, S を表し、X = ∫Xν である。 　 　輻射　 　輻射方程式のモーメンタム方程式は、 　 u/c ≪ 1 の場合上式は簡単化され、 　 となる。

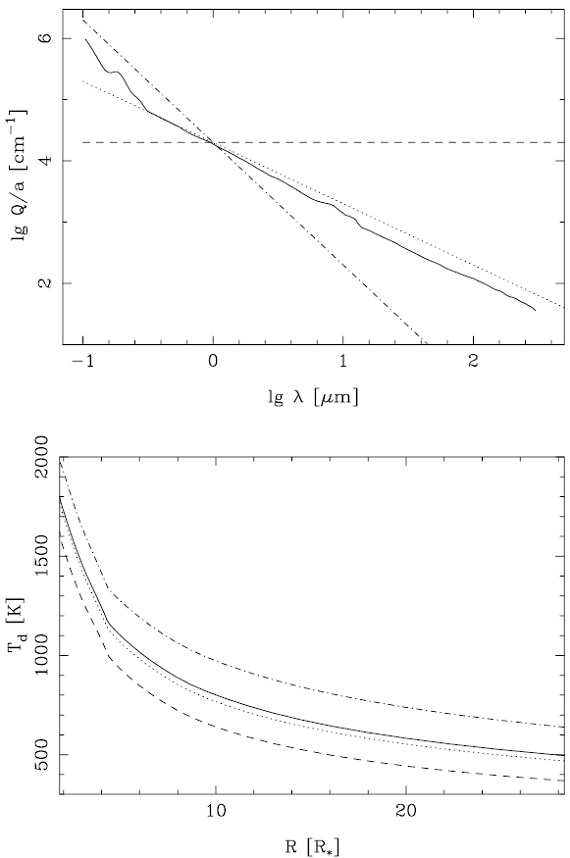
表１．シンボルのリスト ただし定式化は他の応用も考え、元のままで行った。今回のモデルに は Jorgensen1997 の CO, CH, C2, CN, C2H2, HCN 分子オパシティデータを用いた。輻射方程式は 0.25 - 12.5 μm の 51 周波数において定式化された。LTE を仮定し源泉関数は 　 とした。 　状態方程式　 　状態方程式は γ = 5/3, μ = 1.26 の完全気体とした。

２．１．２．ダスト形成　 　ダストの形成と成長　 　Kj = グレイン半径の j-次モーメント。K0=数密度。 また、K3/K0 = 平均粒子体積に比例する。モーメント を用いてダストの成長を追うと、 　 核形成、グレイン成長、蒸発は C, C2, C2H, C2H2 との反応を通じて行われる。 　吸収係数　 　グレイサイズが小さい場合、Qext/agr は agr に依らなくなる。その時、 　 ここに、n(agr)dagr = 半径が agr と agr+dagr の間にある粒子の数密度である。上式の最後 は K3 に比例する。 　Qext/agr　 　この論文で用いた Qext/agr は Rouleau, Martin 1991 から採った。オパシティ以外は Hofner95 と同じ表式を用いている。

ダストとガスの相互作用　 　簡単化と前論文との比較のため、ガスとダスト間の運動量交換は瞬時に行わ れると仮定する。一方で、ガスとダストの間での内部エネルギーの交換は、 夫々の成分が独立に輻射場と行う相互作用に比べると無視できる、 （Gauger et al 1990） (ダストとガス分子衝突で、運動量 は渡せても、ダストの温度は伝わらないのか？ふーん。ガッカリ！ ) その結果、 　 ここに、S(Td) = B(Td) = Td4σ/π で 　 　ダスト形成　 　現在 O-リッチ環境でのグレイ形成の記述は得られていない。そこで、Bowen88 では、M-星において、ダストなしか、またはダストオパシティを以下の様に パラメター化して表現する。 　 ここに、κdmax ＝極大ダスト質量吸収係数、 δ = 階段巾である。Tcond = 1500 K、δ = 600K とした。 (ngr の表式なら分かるが、 質量吸収係数にこの表式は何だ？ ) この表現は定性的な性質の理解には役立つが、そこから定量的な結論を導くことは 無理である。

２．２．数値解　 　２．３．初期モデルと境界条件　 　初期モデル　 　図１は初期モデル 152t30c11u2 の上＝ ρ - T 構造と下＝ 合成スペクトルである。ダストなしモデルが大気モデルと良い一致を 示すことが判る。 　内側境界　 　内側境界 Rin(t） は周期 P 速度振幅 Δup でサイン曲線 型の運動を繰り返す。内側境界光度は Lin(t) ∝ Rin2(t) で変化する。つまり、内側境界面を通過するフラックスは一定とする。 　外側境界　 　静止モデルでは外側境界は 1.5 R* で十分であった。しかし、星風が始まると それに伴い外側境界位置は伸びていく。最後は 20 - 30 R* にまで達した。

図１．初期モデル l52t30c11u2 の上： ρ - T 構造。 下：合成スペクトル。黒線＝モデルから。灰色線＝対応する L, Teff,log g からの　ＭARCS モデル。

　３．構造と力学　

３．１．ダストフリー動的大気　 図２．質量層位置の時間変化。上：l70t28c14u2. 下：l70t28c14u4. 上と下の違いはΔup のみである。 上モデルでは、大気浮揚が不十分でダスト形成とマスロスは起こらない。 下モデルはどちらも起きる。 　分子吸収による冷却効果　 　図２は質量層位置の時間変化を示す。上図の l70t28c14u2 はダスト形成には 不十分な例である。図３にはこのモデルの数位相における物理量の分布を示す。 図３のパネル (d) はガス温度 Tg と輻射温度 Tr の比を示す。 　 ここに、 S(Tgeq) = B(Tgeq) と Tr は式(18) で定義 されている。灰色オパシティではこの比は１である。しかし、非グレイの場合、 光球より外側では分子吸収が, 星からのフラックスピークより長波長側の NIR と MIR 吸収（発光）係数が大きく、外層で強い冷却源として働く。 　以前の論文との違い　 　源泉関数にプランク関数を使用するので、オパシティ κS はプランク平均である。図３ｄは従って、κJ が κS から離れると大気のエネルギーバランスにどう影響するかを教えてくれる。

図３．l70t28c14u2 の異なる変光位相における動径構造。 このシリーズの以前の論文では、 κJ と κS の双方にプランク平均を適用 してきた。プランク平均は高目の κJ を与え、結果ガスへの 輻射圧を大きくする。 　まとめると　 　周波数別の輻射方程式は外層を低温、高密度にする。それはダスト凝結と 、そして星風の起動に有利に働く。

図４．モデル l70t28c14u4 の色々な変光位相に対する動径構造。 実線は静水モデル。

図５．モデル l70t28c14u4 の色々な変光位相に対する動径構造。 実線は静水モデル。

３．２．ダスト駆動星風　 　モデル l70t28c14u4 の静水スタートモデルは l70t28c14u2 と同じである。 違いはピストン運動の振幅で、外側外層はダスト形成が可能なほど、低温で 高密になる。ダストに働く輻射圧は星風を 11 km/s まで加速する。そのマス ロス率は 2 10-6 Mo/yr である。 　３．２．1.ガスとダストの温度　 　非灰色効果　 　図４(d) は Tg/Tr を示す。分子の冷却が働き、静水平衡の Tg は Tr より 著しく低い。ダスト形成の R = 2 R* 付近で非灰色効果が最も大きく働く 事に注意せよ。 (そう言われても何なのか理解できない、 ) 　Tr < Td　 　図５(c) には Td を示す。ガスと異なり、Tr < Td である。これは amC のオパシティが 1/λ で変化し、ダストの吸光も放射も輻射 ピークより短波長側で強いからである。 　オパシティ則の効果　 　図６には仮想的なオパシティ則に対する　Td 分布を示す。 　３．２．２．輻射圧とマスロス　 　図５(d) には χH=実際のフラックス平均ダストオパシティ と χGrey=灰色ダストオパシティ との比を示す。 ダストに働く輻射圧が灰色に比べ 2 - 3 倍になることが判る。

図６．上：実線＝amC. 点線＝Qext' ∝ λ-1. 一点破線＝Qext' ∝ λ-2.　破線＝一定。 下：上のオパシティに対する温度分布の違い。

　４．観測　

図７．上：グレイモデル P13C14U4 極小の合成スペクトル。 上中：波長依存モデルl13t27c14u4。下中： R Scl. 下：　R Lep. 灰色モデルがあまり良く合わないことに注意。 　スペクトル　 　図７には P13C14U4 ＝プランク平均ガスオパシティモデルと 波長依存モデルl13t27c14u4を較べた。グレイモデルのフィットが悪い。 図８では二つのスペクトル領域での比較を示す。

図８．黒：灰色モデル P13C14U4 極小の合成スペクトル。 赤：波長依存モデルl13t27c14u4。 緑：R Lep

　５．結論