Mass-Losing Semiregular Variable Stars in Baade's Windows

　アブストラクト　

１．イントロダクション　 　現在、脈動とダスト輻射圧の結合がマスロスの原因と考えられている。 基本メカニズムは脈動に伴う周期衝撃波が大気外層を広げ、ダスト形成半径で のガス密度を上げ、ダスト輻射圧の効き目を増すというものである。この筋書 きに基づき、ミラ型のような大振幅脈動星の動力学計算も行われている。 　しかし、AGB 変光星の多くはミラ程に振幅が大きくないセミレギュラーで ΔV < 2.5 mag である。ミラ型星は周期的衝撃波から生じると考えら れるバルマー輝線を示すが、セミレギュラーからは周期的輝線が検出されない。 その上、ミラ型星が示す赤外域でのライン分裂 ( Hinkle, Lebzelter, Scharlach 1997 ) がセミレギュラーでは見られない。 　これまでセミレギュラーの詳細な研究は数個の明るい、しかし距離不定な星 を除いてなかった。しかし、MACHO, OGLE, Hippparcos によりその構図は大き く変わりつつある。一方、 ISOCAM が中間赤外データを提供している。特に、 バーデの窓では 15 分角四方内に 1193 天体を 7, 15 μm で検出した。 その結果、中期 M から晩期 M、さらにミラ型星に至るマスロスの連続的な 系列のサンプルが得られるようになった。 そこで、我々はバルジ AGB 星の 新しい研究を開始した。それは MACHO の可視変光曲線と ISOGAL の中間赤外 測光を結びつけ、質量放出 AGB 星のだ大規模サンプルの解析である。

２．データ　 　２．１．ＩＳＯＧＡＬデータ　 　２．２．ＭＡＣＨＯデータ　 図１．NGC 6522 と Sgr I の窓 15 分角四方での ISOGAL CMD. [7-15] - F15 の特徴的な系列に注意。黒丸＝ミラ。十字＝MACHO 前データで変光非検出。 RGB 先端は1 [15] = 8 mag. それより上は AGB 星。

　３．ＭＡＣＨＯと ISOGAL の同定　

１． V < 13.5 + 4.67(V-R) で暗い主系列星を落とす。4 万個残る。 ２．(V-R) > 1.5 星で予備同定し、そのズレのメディアンをオフセット。 ３．1193 ISOGAL 天体の 3" 以内の最近距離 MACHO 天体。 図２．ISOGAL-MACHO 間座標の差 (arcsec). 斜線＝わざと15" ずらしたリストで作った時の同定＝偶然の一致がどのくらいあるか。

同定＝904/1193 ISOGAL. 非同定ISOGALは観測ミス天体？以降の 解析は V, R, 8, 15 測光の揃った 332 天体に行う。 図３．MACHO/ISOGAL 同定天体の VR ＣＭＤ．　黒丸＝ V, R, 8, 15 が揃う。 (V, V-R) = (13, 0.9) RC 付近の塊りは偶然の一致同定だろう。

図４a．左：５つのミラ型星 MACHO R 光度曲線。右：左データを位相で揃えた。

図４b．左：５つの SRa 星 MACHO R 光度曲線。右：左データを位相で揃えた。

図４c．左：５つの SRb 星 MACHO R 光度曲線。右：左データを位相で揃えた。

図４d．左：上＝２つの二重周期星 MACHO R 光度曲線。下＝３つの大振幅 SRa 星。 右：左データを位相で揃えた。

　４．変光の特性　

４．１．周期　 　サンプル星のうち 305/332 = 92 % は周期的または準周期的変光を示した。 振幅はあまり大きくなく、より長い期間の不規則な変光がそれに被さっている。 残りの 27 星中 26 は MACHO が飽和してよい変光曲線が得られなかった。1 星 は食連星である。この領域には既知のミラ型星が 14 ある。 SR 星はその 20 倍 見つかった。 　４．２．セミレギュラー　 　log P = 2.2 で区切り　 　 332 星の光度曲線全てが調べられた。周期の近似値を直視でまず決め、次に フーリエ解析でより正確な値を求めた。観測に季節的な重みがかかるので、 log P < 2.2 の変光 280 星はシーズン毎に周期解析を行い、その後振幅周期図で まとめた。残り 25 星 は log P > 2.2 である。 　SRa と SRb　 　SRa は P = 35 - 1200 日で、周期はほぼ一定であるが、ミラ型星より振幅が 小さい。 SRb は = 20 - 2300 日だが、周期星はやや弱く、不規則変化も示す。 通常は平均周期を適用する。 　我々のサンプルの 3/4 は SRa で残りの大部分が SRb である。しかし、この 分類自体はかなり主観的である。周期が長くなると SRb の割合が増える。 　４．３．ミラ　 　既知ミラの同定　 　１４既知ミラ中６個は表２にあるように、明確な変光曲線が得られた。５個は MACHO がサチって、MACHO カタログに載っていないので、 332 サンプル中にない。 残り３個は同定ミスで近くの暗い星とされていた。 　周期精度　　 　MACHO 周期を Lloyd Evans 1976 や Glass et al 1995 の値と較べた結果、 ΔP/P = 0.07 - 0.09 であった。

表２．ミラ型星リスト

　４．４．周期光度関係　

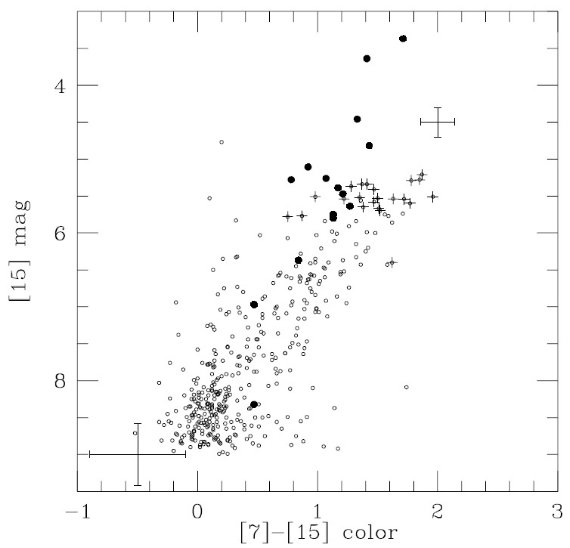
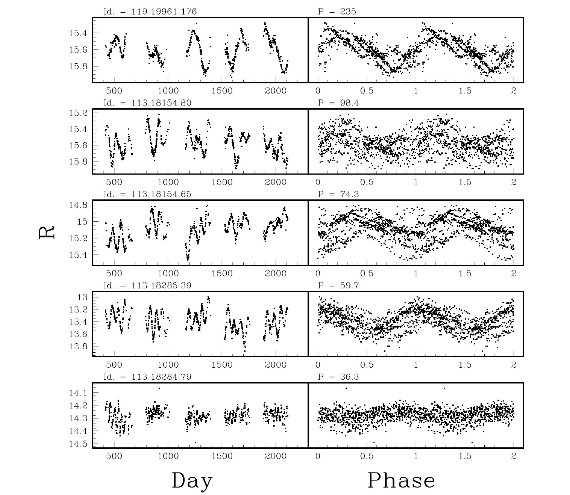
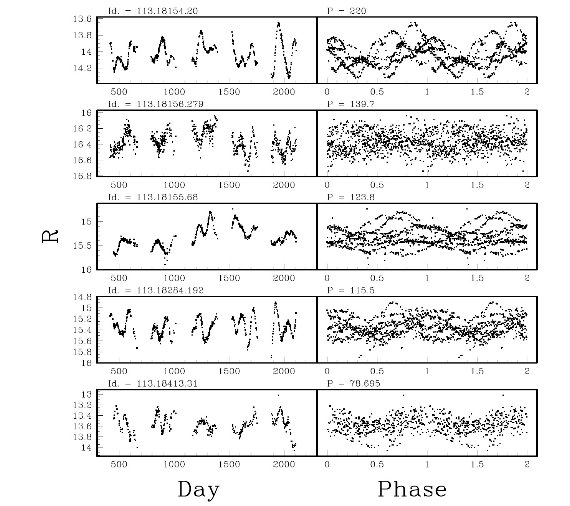
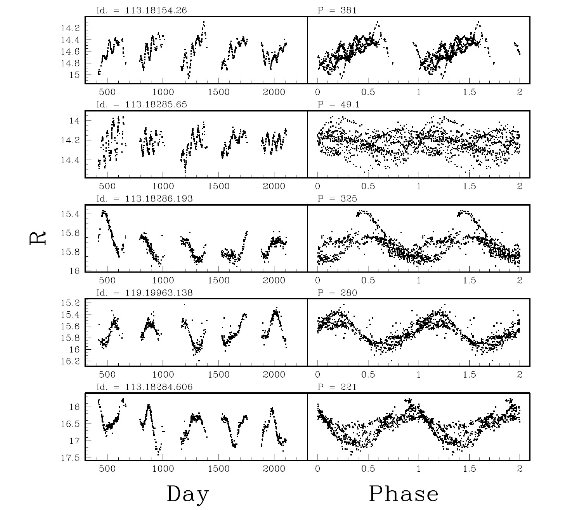
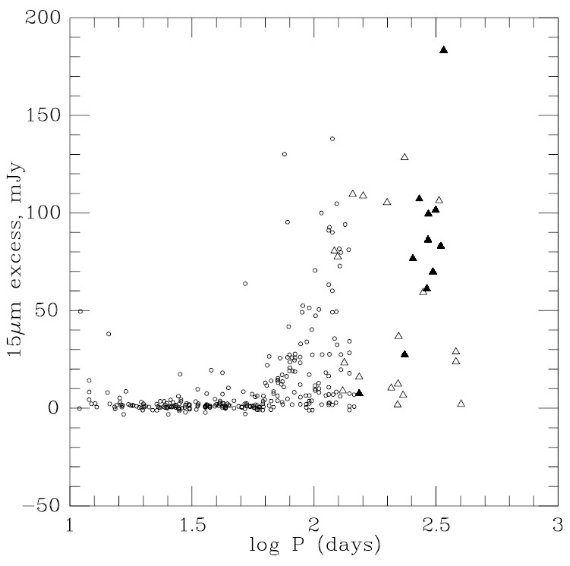
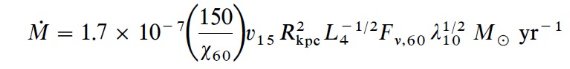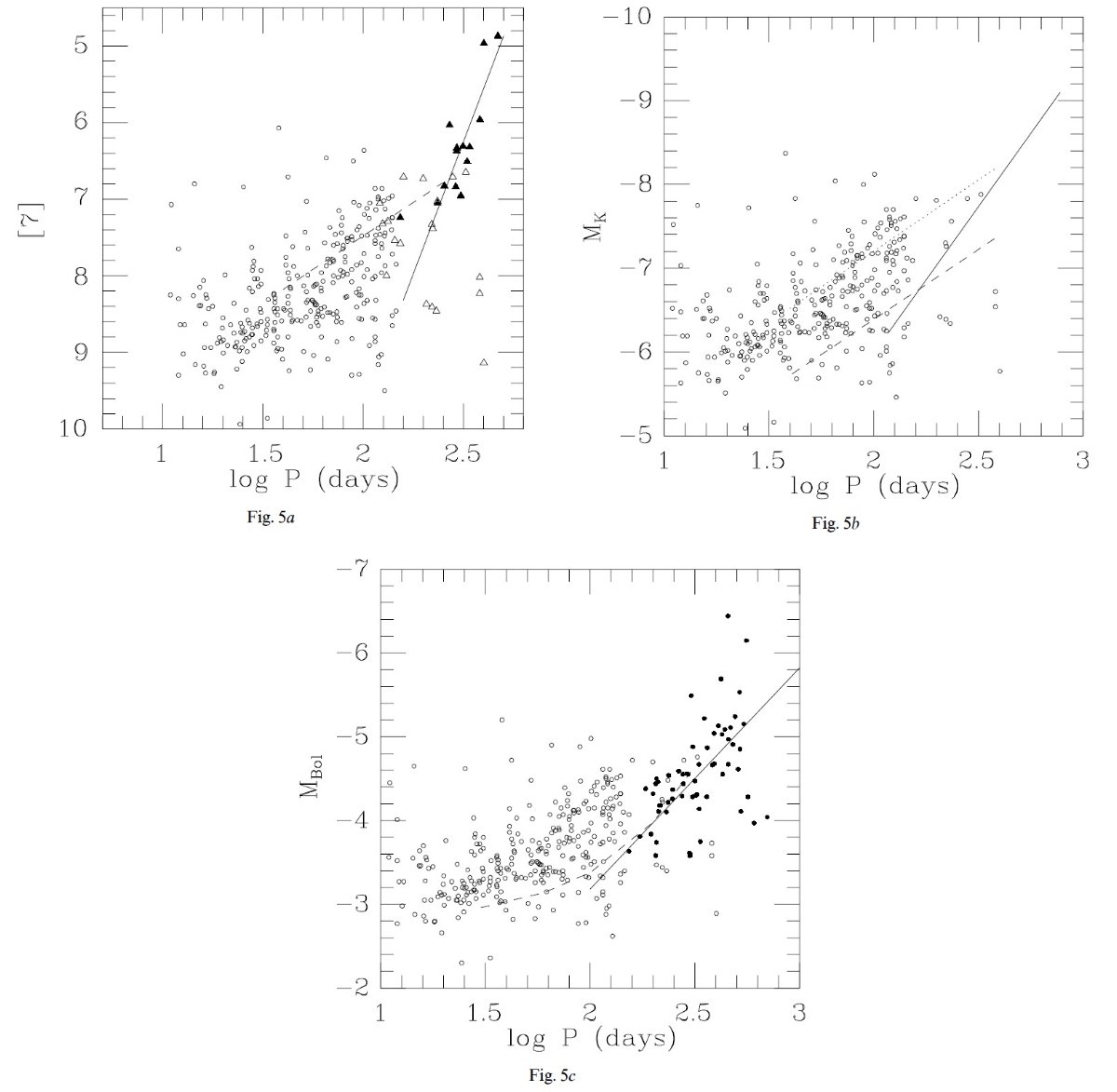
ＳＲの log P - [7] 関係　 　図５a は我々のサンプルの log P - [7] 関係である。K と同様に [7] も Mbol と相関が強い。参考のために図中に Bedding, Zijlstra (1998) のヒッパルコス SR 星の関係を重ねた。このためには NGC 6522 領域での 51 晩期型非ミラ型星の Ko （Frogel, Whitford 1987）と ISOGAL の [7] から導いた [7] = 1.04 Ko - 0.20 を使用した。 (カラーの補正はナシ。 ) バーデの窓の DM = 14.7 とした。Bedding, Zijltsra 1998 ラインは、 　　　[7] = -1.85 log P + 11.27 となる。このラインはサンプル点の真ん中(ほんとは少し上)を通っている。こ のラインは Whitelock 1986 が球状星団の log P = [0, 2.8] の変光星に対し て最初に見つけた関係より 0.8 mag 上を通っている。 　ミラの log P - [7] 関係　 　図５a にはミラに対する関係式 　　　[7] = (-6.9±1.4)log P + (23.5±3.4) も重ねた。SR と違いミラの [7} はダスト放射が含まれているので、Mbol の物差しにはなりにくい。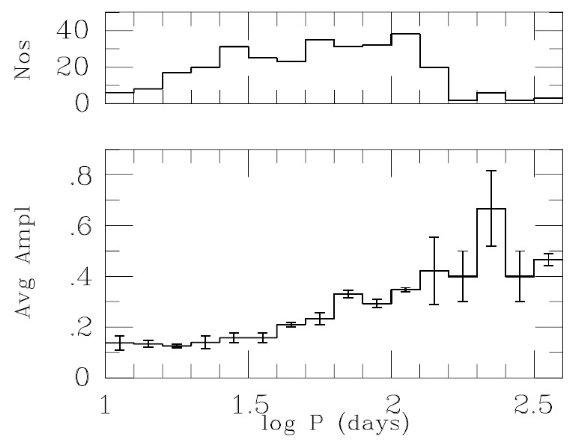　 　図５b = log P - Ko 関係　 　ミラの Ko にはダスト放射はあまりないので、 Mbol の指標には向いている。 そこで、[7］を　Ko に変換して SR の log P - Ko 関係を図５b に示した。 (図５a をずらしただけの絵になる？ ) 図中には Bedding, Zijlstra 1998 と Whitelock 1996 のラインも引いた。 (LMC の　PLR との関係は？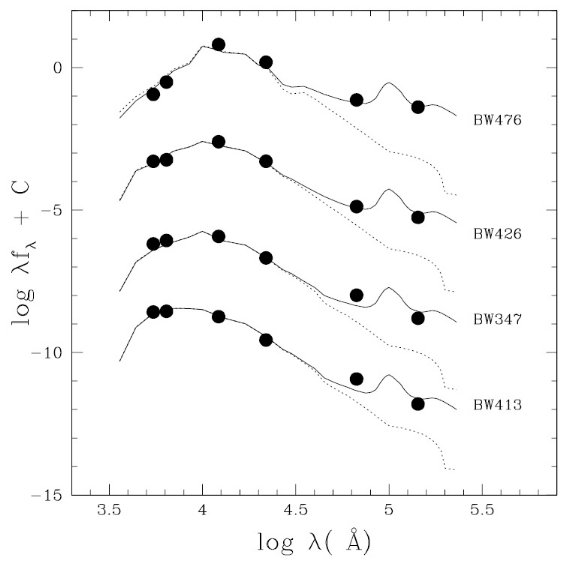 ) 　図５c = log P - Mbol 関係　 　図５c は log p - Mbol 関係を示す。そこでは上の関係を使って、SRs の [7] を Mbol に変換した。Glass et al 1995 のミラ PLR も重ねた。図５ a, b, c で SR の PLR 勾配がミラに較べ緩いのは進化系列を反映しているのかも知れ ない。そのように緩い進化経路は、今回より狭い log P = [1.8, 2.8] 範囲で だが、Vassiliadis, Wood 1993 が提案している。Alves et al 1998 も同様な 進化経路を P - L 図上に描いた。彼らは Vassiliadis, Wood 1993 モデルを 解析的に内挿して、初期質量とメタル量に依存する P-L 関係を導いた。彼らは メタル量は似ているが年齢の異なる 47 Tuc と NGC 1783 で SRs の性質が モデル P-L 系列の相対的光度を支持しているとした。 　SR から Mira へ　 　セミレギュラーは P - L 面上を星毎にほぼ平行な進化経路に従って進み、 ついにミラ系列に達する。銀河系球状星団ではそれは P = 200 d 付近に生じる。 太陽近傍の星では P = 460 d 付近になる。太陽近傍ミラの周期分布は現在知ら れていない。 ("solar neighbourhood line" は不明確。 今 2016 太陽近傍 P 分布は？ )

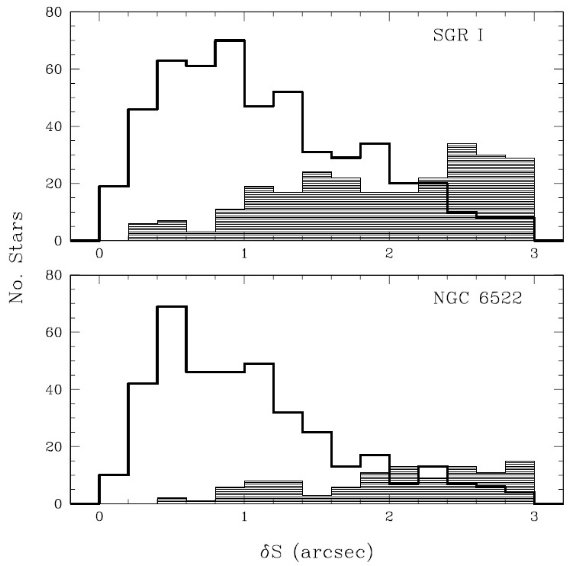
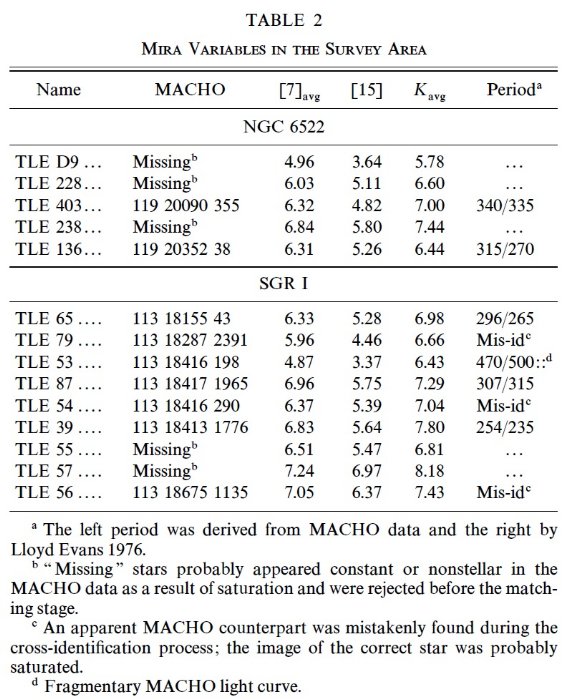
図６．上：log P 分布ヒストグラム。下：log P 区間毎の平均振幅。 ミラは省く。散布度も重ねた。 しかし、 Sgr I バーデ窓領域の調査は完全で(Glass et al 1995) その平均周期は 346 d である。この値は球状星団ミラでの平均値 200 d よりずっと大きく、また バーデ窓でホワイトロック 1986 P-L 系列の上にあるセミレギュラーと一致する。 　ＳＲの Ko 散らばりの意味　 　Sgr I バーデ窓ミラ型星の log P - Ko 関係の周りの散らばりは 0.35 mag である。その大部分は視線に沿ったミラの分布、= バルジの厚み、が原因で ある。図５a の SR 散らばりはそれよりずっと大きいということはなく、進化 経路の巾があまり大きくないことを意味している。 　振動モード　 　図６上から分かるように、SR の周期にはっきりした集中は見えない。しかし、 図５a, b, c ではミラとセミレギュラーの間には Wood, Sebo 1996, Wood 2000 が LMC で述べたものと似た間隙がある。この間隙は、しかし、MACHO 観測で 季節性による周期もどきが起きる周期に相当する。Wood, Sebo 1996, Wood 2000 はミラ系列を基本振動でセミレギュラーは高次振動ではないかとしている。 第１倍音振動は基本振動の左 Δlog P = 0.35 の所にミラ系列と平行に 並ぶはずである。LMC にはより高次の振動系列が明白に見えるが、バーデの窓 では観測誤差が大きいのと、距離が様々なためそれほどはっきりした分離は見え ない。ＳＲの短周期端では非常に高次の倍音振動が必要であるという議論は Koen, Laney 2000 が行っている。

　４．５．振幅　

　５．質量放出率　

　５．１．ＳＥＤ　

距離既知セミレギュラーの最初の中間赤外研究　 　サンプル中 Frogel, Whitford 1987 が同定した星の SED をモデルフィット した。それらの星はモデル SED を用いて 15 μm 超過をに基づく質量放出 率の較正に使われる。また、我々は質量放出率が光度や有効温度にどう依存 するかを調べる。これは距離が知れたセミレギュラーの中間赤外測光の最初 の研究である。我々は脈動の性質と質量放出を較べる。 　大気モデル　 　Frogel, Whitford 1987 の表１から選んだ、25 SRs + 1 Mira = 26 星の Jo, Ko から SED と Mbol を求める。Mbol は以前議論したように DM = 14.7 を考 慮して -0.5 mag の調整を加えた。赤化補正には Av = 1.5, AR/ AV = 0.75 を仮定した。有効温度は (V-K)o に Bessell et al. (1998) を適用して定めた。星本体の SED は Lejeune, Cuisinier, Buser 1997 の モデルスペクトルを、太陽 [Fe/H], log g = 0.28, 0.00, Teff = 2500, 2800, 3000, 3200, 3350, 3500, 3750, 4000 K を集めた。注意しておくが、これらは 静止モデルであり、脈動の結果の大気の拡大は考慮されていない。 (このモデルとBessell et al 1998 は 同じ Teff - (V-K) 関係を与えると書いてあるが、理屈が分からない。) 　DUSTY の入力と出力　　 　このモデルスペクトルを DUSTY コードに入力する。グレイン成分にはシリケ イトを採用した。また、ダストシェルの内側温度は 1000 K に固定した。 等々で計 200 の DUSTY モデルを計算した。DUSTY は L = 10,000 Lo に規格化 した質量放出率、膨張速度を出力する。真の値はこれにスケーリングして求める。 　フィット　 　表３にはフィットの結果を示す。表の第６，７列には 10,000 Lo に対する Tmod と (dM/dt)L4 が示されている。スケーリングした (dM/dt) は第８列 に載っている。図７にその内の４例を示す。

図７．黒丸＝４つの星の観測例。実線＝ DUSTY モデル。点線＝星本体。

５．２．質量放出率、有効温度、光度　 　質量放出の温度、光度依存性　 　表３の結果を (dM/dt) ∝ TαLβ の 形でフィットした結果は α = -8.80-0.24+0.96, β = +1.74-0.24+0.16 であった。 Arndt et al 1997 による炭素星質量放出率のモデル計算では、 (dM/dt) ∝ T-8.26L1.53 であり、今回の結果と 良く合っている。 　５．２．15 μm 測光からのダスト放射質量放出率　 　赤外超過から質量放出率　 　表３は F(7 μm) からレーリージーンズ外挿した星フラックスに対する 15 μm 超過 x[15] を載せている。この量と DUSTY で導いた質量放出率と の間の関係は 　　　log (dM/dt) = (0.87±0.08) log (x[15]) - (7.88±0.11) である。

この式によると SRs の 15 μm 超過が 3 - 130 mJy は質量放出率 10-8 - 5 10-7 Mo/yr に相当する。説明した通り、 これは 7 μm からレイリージーンズ外挿した上の超過を仮定していて、 シェルが短波長で光学的に厚い場合は適用できない。 　ユラの式　 　ユラ１９８７は次の質量放出の式を発表した。 　この式と我々の結果を較べてみた。F(15) を F(60) に変換するため、 Jura 1986 の炭素星に対する式 F(ν) ∝ ν1.54 を転用した。色々数値を仮定して計算すると、15 μm 超過 100 mJy に対し 質量放出率 2 10-7 Mo/yr が得られた。我々の較正式は 4 10-7 Mo/yr なのでこの値はかなり良い。

５．４．質量放出率と周期　 　図８は [15] - log P 関係　 　図８には 7 μm からのレーリージーンズ外挿を仮定して、その上の超過分 x[15] と log P との関係を示す。図にはミラも含めた。周期が長くなると 外挿の前提が怪しくなることに注意。 　大振幅は質量放出の必要条件でない　 　長周期セミレギュラーの質量放出率はミラのそれと重なっている。これは 質量放出に大振幅脈動が必要でないことを物語る。P < 60 d で目立つ 質量放出がないことは Kerschbaum et al 1996 の P < 75 d に CO が検出 されないという発見と合致する。 　５．５．CO との関連で　 　歴史　 　Kahane, Jura 1994 は 11 SRs (P=[100, 160] d) から CO を検出した。それ らは K = 0 より明るい。彼らはそれらの質量放出率を 1 - 1.5 10-7 Mo/yr と求めた。似た結果が p = [300, 400] d ミラで求まるので、 SRs は 基準振動するミラに対応する倍音振動星ではないかと思われた。Kerschbaum et al 1996 は彼らのサンプルを ARa と SRb に広げた。Kerschbaum, Hron 1992 は青い SR では CO を検出しなかった。一方赤い SR とミラでは検出率は 50 % であった。 P < 75 d と P = [175, 325] d の SRs では CO が検出されないが、 P = [75, 175] d では CO が検出される。Young 1995 による近傍の薄いダスト シェルを持つミラの研究によると、M5.5 より晩期型の星でのみ CO が検出され る。M7 より晩期では検出率は 100 % になる。

図８．15 μm 超過と周期の関係. P > 70 d が質量放出の必要条件。 しかし、十分条件ではないことが判る。

　５．６．質量放出率と光度　

SRs の質量放出が T と L の関数であることを見てきた。高い光度と 長い周期は共に低温と結びついていて独立な変数ではない。図９には われわれの SRs と van Loon et al 1999 による LMC のダスト AGB 星 の結果を合わせた。合わせると (dM/dt) ∝ L2.7 となる。

図９．(dM/dt) と Mbol の関係。四角＝バーデ窓のセミレギュラー。 黒点＝LMC C 星。白丸＝ LMC M 星。バツ＝ LMC 超巨星。実線 ＝直線フィット。

　６．結論