Model atmospheres broad-band colors, bolometric corrections and temperature calibrations for O - M stars


M.S. Bessell1, F. Castelli2, and B. Plez
Astron. Astrophys. 333, 231-250 (1998)



　アブストラクト　

大気モデルからの広帯域カラーと輻射補正　

Johnson-Cousins-Glassシステムでの広帯域カラーと輻射補正（ベッセル1990; ベッセルとブレット1988）をクルツ（1995a）、カステッリ（1997）、Plez、 ブレットとノードランド（1992）Plez（1995-97）とブレット（1995a,b）の 新しい大気モデルからの合成のスペクトルを使って計算した。これらの大気は、 現在進行中のより大きな格子の代表例である。

大気モデルと観測の比較　

我々は異なる格子間の差を議論し、理論上のカラー-温度関係を以下の４つから 導き出した基本的カラー温度関係と比較する：

(a) 赤外フラックス法（IRFM）：A- K型星に対して（ブラックウェルとLynas- グレイ1994;アロンゾほか1996）そして、Ｍ型矮星は（辻ほか1996a）


(b)月の掩蔽（リッジウェイほか1980）

(c)マイケルソン・インターフェロメトリー：K-M型巨星に対して（ダイ・ベネデ ットとRabbia 1987;ダイクほか1996;ペリンほか1997）

(d)食連星：M型矮星。

輻射補正と温度・カラー関係　

カラー・カラー関係とカラー輻射補正関係を比較して、幾つかのカラー以外では 晴らしい一致を見出した。新たなモデル格子による、より現実的なフラックスと スペクトルは、精密な種族合成モデルと非標準タイプの測光帯域の手早い較正を 可能にする。また、理論上の輻射補正と温度・カラー関係は、観測されたカラー 等級図から理論上のHR図への信頼できる変換を許すだろう。

　1.イントロ　

(カラーと等級) から (光度と温度) への観測関係式　

　多くの場合、恒星の光度と温度は観測カラーと等級から導かれる。 通常は、観測的なカラー温度関係とカラー・輻射補正関係を用いて、 （観測等級、カラー）から（温度、光度）へと変換する。

それらの例としては、
輻射補正：　Schmidt-Kaler 1982;Reid & Gilmore 1984;
　　　　　　Bessell & Wood 1984; Tinney et al.1993
温度：Bessell 1979,1995; Ridgway et al.1980;Di Benedetto,Rabbia 1987;
　　　　Blackwell & Lynas-Gray 1994(BLG94); Tsuji et al. 1995, 1996a;
　　　　Alonso et al. 1996(AAM96); Dyck et al. 1996; Perrin et al. 1997

　ただ、上の研究は様々な金属量のＦ０−Ｋ５矮星を調べたＡＡＭ９６以外は対象 が太陽メタルの巨星と矮星に限られている。

モデル関係式の必要性　

　したがって、モデルでもっと広いパラメター空間、温度、重力、組成をカバー する必要がある。観測データは太陽組成モデルとの比較に使用して、限定された パラメター領域でのモデルの正しさをチェックする。それは、全パラメターに 対するモデルの妥当性を含意することになる。

大気モデルの改良　

モデル大気のグリッドとして過去２０年間, ＭＡＲＣＳ(Gustafsson et al 1975) とATLAS（Kurucz1979）が用いられてきた。MARCS モデル測光値に関しては、 Gustafsson,Bell 1979, Bell,Gustafsson 1989 が、ATLAS　については Buser,Kurucz 1978 が研究した。しかし、ライン数の不足、中間温度でのセミ コンベクションの扱いの不備が最近問題となってきた。

そこで、モデルの改良が行われた。Kurucz 1993, 1994 は　ATLAS9 において O - K 型星のモデルとカラーを発表した。モデルの対流の扱いは Kurucz 1995a において改善された。Castelli 1997 はそれとは別の対流モデルを使い、 ATLAS9 のサブグリッドを作った。これを完全なものにする試みは継続

中である。 Plez et al. 1997 による MARCS モデルの改良版 NMARCS を A - M 型星に 広げる作業も進行中である。

改良モデルの利用　

我々は上に述べた計算の予備的な結果を入手した。フラックス、合成カラー、 輻射補正は古いモデルに較べると大きく改善されている。モデルグリッドが 完成すれば、種族合成モデルは素晴らしい精度を獲得し、また非標準的な測光 システム、例えば HST や Hipparcos, の等級の較正も正確になるだろう。 ここで用いるＵＢＶＲＩＪＨＫＬカラーはBessell et al 1990パスバンドによる、 Johnson - Cousins UBVRI 測光と Bessell, Brett 1988 による Johnson-Glass JHKL パスバンドを使用して計算されている。

付録の内容　

　付録では合成測光を行う際の問題点を詳細に論じた。
付録Ａ、Ｂでは UBVRIJHKL カラーが Vega と Sirius を用いてどう規格化される かを述べた。

　付録Ｃ，Ｄでは輻射補正のゼロ点を導いた。 輻射補正 BCX は、mbol = mX + BCX で定義される。ここに、X は問題にしているパスバンド名である。
太陽の絶対輻射等級 Mbol = 4.74 を仮定 し、V๏ = -26.73 (Stebbins, Kron 1957)から導かれる MV = 4.81 を使うと、太陽モデルに対して BCV = -0.07 でなければならない。こうして、BCV のゼロ点が決まった。

注意すべきなのは、この値が Kurucz 1979, 1993, 1994 が用い、Schmidt-Kaler 1982 が踏襲している -0.193 と異なることである。

　付録Ｅでは一般的には標準システム全般、個別には UBVRI システムを実現する ことを論じた。ここでの議論に基づいて、我々は U-B カラーを 0.96 倍に することに決めた。この論文ではこの 0.96 倍にされたカラーが用いられている。 他のカラーは調節されていないが、標準システムには非線形なカラー項が多分 含まれているので、非常に高温、低温の星に対しては調整が必要であろう。
分かったような、分からないような。

　２．モデル大気　


　２．１．ＡＴＬＡＳ９　

クルツモデルのグリッド　

Kurucz 1993,1994 (ATLAS9) は、温度、重力、組成でのモデル格子 （Ｏ−Ｋ星）を作った。彼のパスバンドとゼロ点は、特に Cousins の R, I バンドでこの論文と若干異なる。
Wood/Bessell1994 は　Kurucz 1993 モデルフラックスから UBVRIJHKL カラーを 計算した。彼らの結果は mso.anu.edu.au at/pub/bessell/ から ubvrijhkl.dat.z で ダウンロード可能である。
Bertelli et al 1994 は上の結果を使用して等時線を作った。
これらのカラーはこの論文の付録Ａで述べる方法とはやや異なるやり方で 標準 UBVRIJHKL システムに規格化されている。この論文では Wood/Bessell1994 を新しい値に置き換えた。

1995 年以前モデルの再計算　
　Kurucz 1993 モデルのＡ−Ｇ型星カラーに見られる不連続は、 Castelli 1996 によりKurucz自身が "approximate overshooting" と呼んだミックシングレングス の扱いが原因であると説明された。1995 年以前の "approximate overshooting" を 用いた対流層の計算は、Kurucz が Castelli の忠告を取り入れて再計算した。

表１ (付録Ａ) には Kurucz 1995 の太陽組成、マイクロ乱流＝ 2km/s, l/H = 1.25 モデル での再計算の結果を載せた。Teff > 8750 K では対流が起きないので、その 温度以下の計算のみが載っている。

表２ (付録Ａ) には、表１と同じパラメターに対し "no-overshoot" の仮定で Castelli が計算した結果を載せた。

オーバーシュートなしがベター　
Castelli, Gratton, Kuricz 1997 は、 オーバーシュートありとなしとで生じるカラーとバルマープロファイルの差を 論じた。「オーバーシュートあり」の方が太陽スペクトルを良く再現するが、 太陽より高温の星全体としては、「オーバーシュートなし」の方がよいという結論 になった。

　話の締めくくりに、表３に Kurucz 1994 の太陽組成、 Te = 8750 - 5000 K, vturb = 2 km/s モデルのカラーと輻射補正を載せた。

　Castelli は低メタル、-0.5, -1.0, -1.5, -2.0, -2.5 で「オーバーシュート なし」モデルを計算した。双方の再計算結果は Kurucz, Castelli により CD-ROM 配布が準備されている。その間、最新 ATLAS9 モデルの結果は kurucz@ckafu3.harvard.edu または、castelli@astrts.oat.ts.astro.it　から ダウンロードできる。

　２．２．ＮＭＡＲＣＳ　

改良された MARCS モデル　

　Plez, Brett, Nordlund 1992 は、改良されたラインオパシティ、球対称性、 化学平衡に入れる分子種の増加を組み込んで、M 型巨星と矮星のモデルを 計算した。モデルは太陽組成で、３種類の大気拡大度と３種類の質量, 1, 2, 5 M๏ を仮定した。質量が大きくなるほど、大気拡大度は 小さくなる。Plez 1995 は、より高温の平面大気モデルを [Z/Z๏] = 0.6, 0.3, 0.0, -0.3, -0.6 に対し計算した。これらのモデルは 　plez@astro.uu.se から入手できる。

TiO, VO, H2O の新しい強度測定　

　Plez 1995 の計算には Doverstal, Weijnitz 1992 による TiO 強度の新しい 計測結果が組み込まれていた。しかし、Hedgecock et al 1995 は電子状態の 寿命が新しい計測では古い値と大きく異なることを示した。Langhoff 1997 は 第１原理計算の結果を実行し、新しい計測値と合うことを報告した。彼は 現在のモデル計算に含まれるすべての遷移に対し電子遷移モーメントを与えた。 V バンドに影響する TiO a-f バンドも最近足された。
　Karlsson et al 1997 は VO の３つの励起状態 A, B, C の寿命を測定し、 状況を大きく改善した。Jorgensen 1996 は H2O のライン リストを提供した。

新しい測定に基づくモデル　

　Alvarez, Plez 1997 はこれらの結果を取り入れて、M 型巨星とミラ型星の 狭帯 カラーを計算し、改善点を完全に議論した。我々はこれら改訂オパシティを 用いてモデルのカラーを再計算することにしたが、しかしながら、モデルの 再収束は行わなかった。（意味不明）
　数モデルで実験を行い、温度構造はスペクトルを決めるのに重要ではないと 判断した。それに、オパシティがさらに改良されると、いずれ温度構造もスペク トルも双方共に変更されるだろう。Plez et al 1997 の次期モデルグリッドは 無矛盾なデータセットを使ったモデルになるであろう。したがって、この時点で 全てを再計算するのは無意味と判断した。
　モデルの不確定性は新しいモデルと 1992, 1995 グリッドと較べると分かる。 log g = 1.5 で、(V - K) の (1992 - 1995)差は、 Te = 4000 K で 0.00, 3800 K で -0.044 である。log g = 0.0 では, 4000 K で 0.076, 3600 K で 0.027 である。(V - I) はそれらが、 0.000, -0.025, 0.039, 0.038 となる。 カラー差は Te = 4000 K 付近では小さいが低温になると増大して行く。新しい 改善モデルの方が観測とは良く合う。

　表４、５（付録A）には Plez et al. 1992 と Plez 1995 モデルのカラーと 輻射補正を載せた。表６（付録A）には Brett 1995 と Plez 1997 の新しい M 型矮星モデルの結果を載せた。


　３．議論　

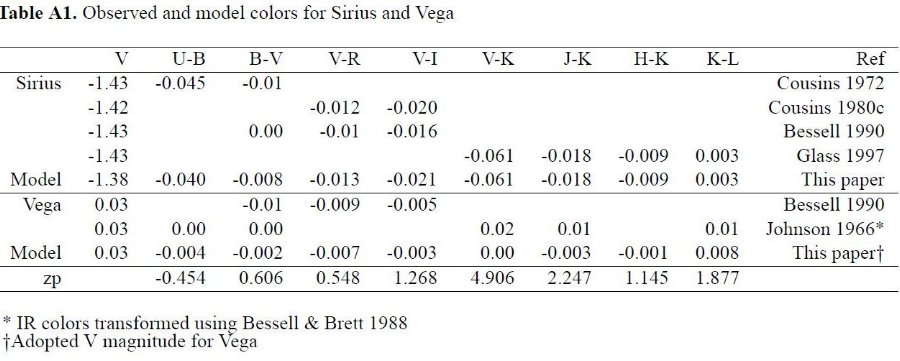
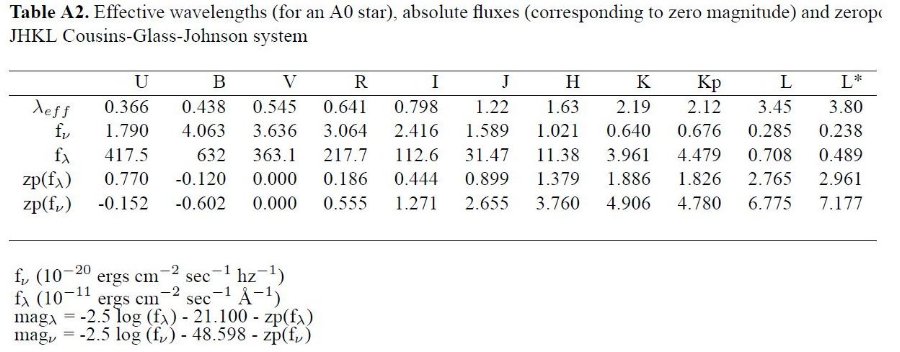
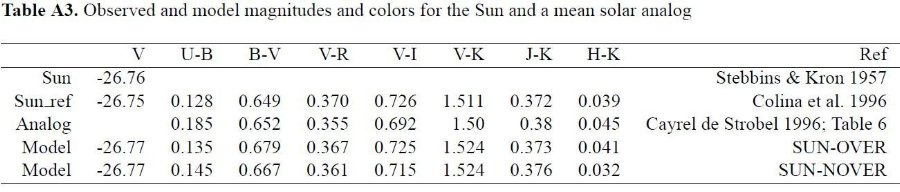
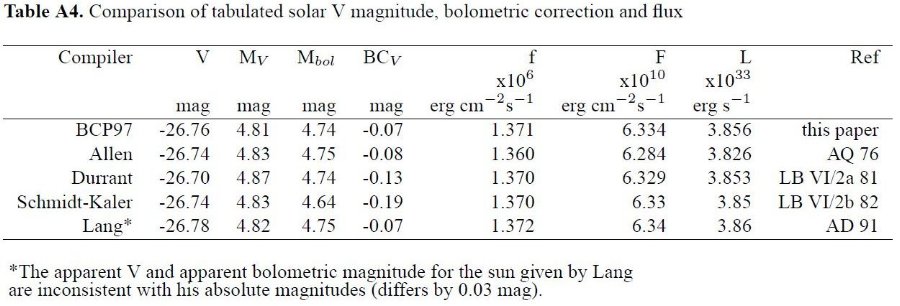
　３．１．経験的温度較正　

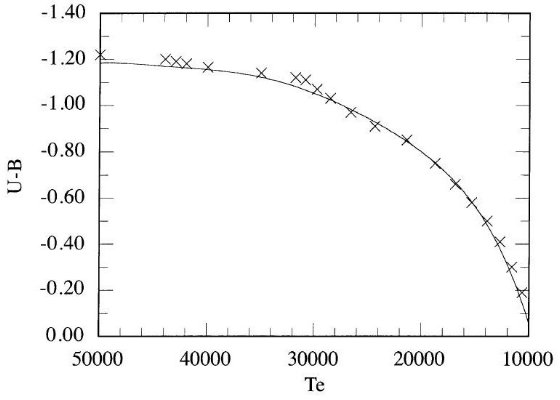
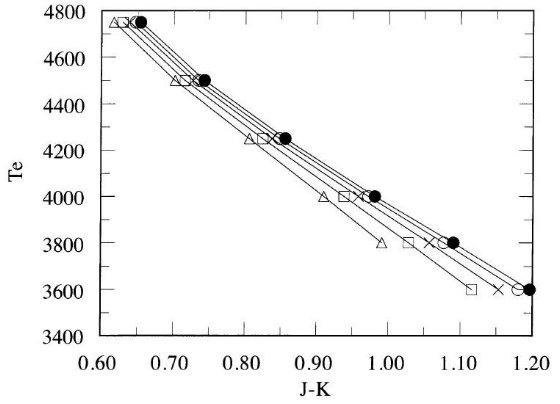
月の掩蔽と干渉計法　

　多くの星で基本温度は不明であり、幾つかの O - F 型星では 恒星強度干渉計により半径が測定され、早期型星の経験的温度較正が Code et al 1976 により与えられた。

　もっと低温の星の半径は月の掩蔽とマイケルソン干渉計から導かれる。 Ridgeway et al 1980 による大きな影響を与えた論文には月掩蔽を使って、 KM　巨星の　Te - (V - K) 関係が導かれている。より最近にはマイケルソン 干渉計が多くの KM 型星の高精度データを与えている。将来、より長い基線長で の観測がより早期型の星の観測値を与えるであろう。

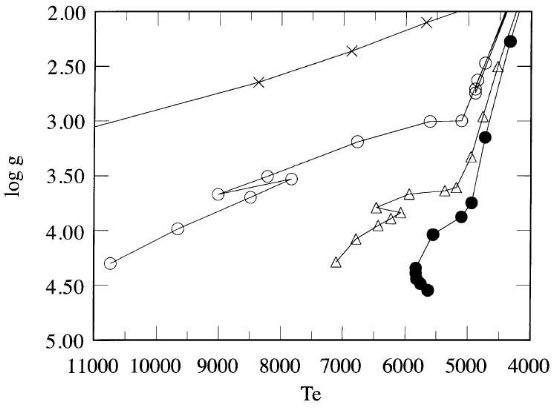
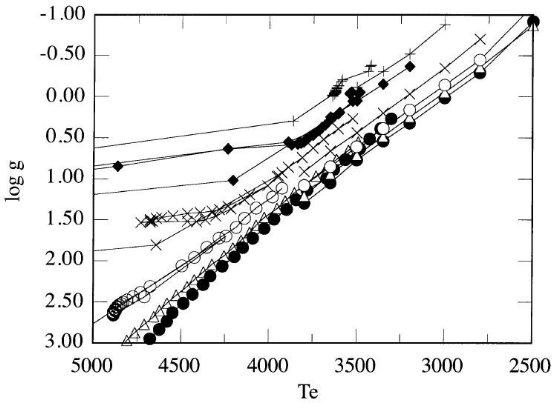
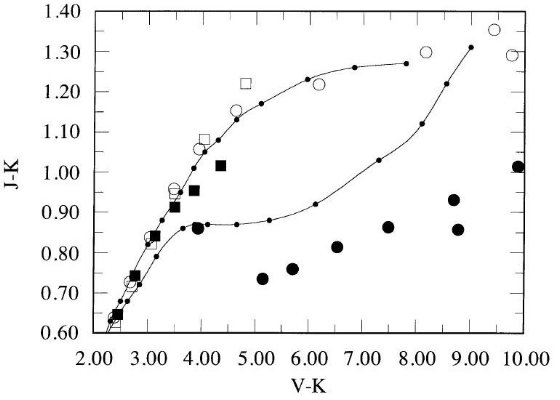
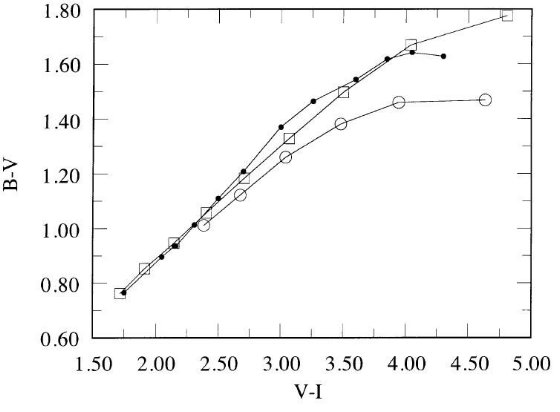
　図１には、Ridgway et al 1980 の掩蔽、Di Benedetto, Rabbia 1987, Dyke et al. 1996, Perrin et al 1997 の干渉計データを示した。 両者の結果はよく一致しているが干渉計の方がはるかに高精度である。図の 短い線は Ridgway et al 1980 が与えた温度スケールである。長い線は 干渉計データの多項式フィットである。 Ridgway et al 1980 スケールには Te = 3300 - 3700 K で僅かな補正で十分であることが分かる。

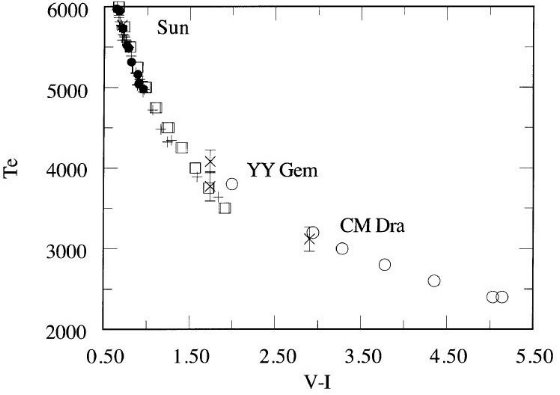
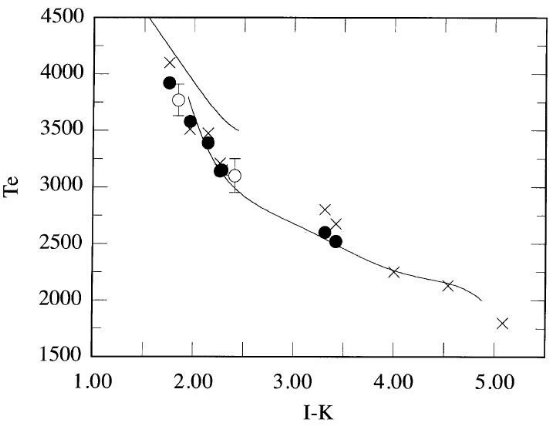
　M 矮星に関しては食連星のデータが２つあるだけでである。後に論じる。

赤外フラックス法　

　最近、赤外フラックス法 (IRFM) が A - M 型星の温度を決める方法として使わ れるようになった。Megessier 1994, 1995 にはその信頼性についての議論がある。 辻はその開拓者であり、炭素星 Tsuji 1981a, Ｍ巨星 Tsuji 1981b, Ｍ矮星 Tsuji et al 1995, 1996a の有効温度を決定した。Blackwell らはより高温度の星を 後半に調べた。Blackwell, Lynas-Gray 1994 (BLG94) は種族Ｉの A - K 巨星と矮星の 温度を IRFM と Kurucz 1992 モデルを用いて決めた。 Alonso,Arribas,Marinez-Roger 1996 (AAMR96) は 色々なメタル量の F0 - K5 矮星の IRFM 温度と輻射補正を定めた。

(V-K) カラーと(V-I) カラー　

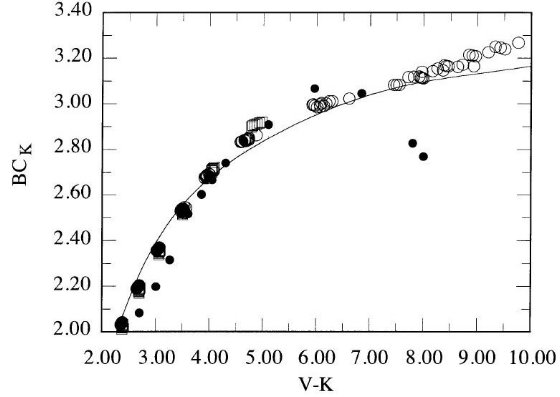
　多くの著者が (V-K) カラーを用いて結果を表わしている。K, M 型星では データも豊富で精度も高いが、A - F 型星では精度が落ち、Te - カラー関係 の不定性の原因となっている。

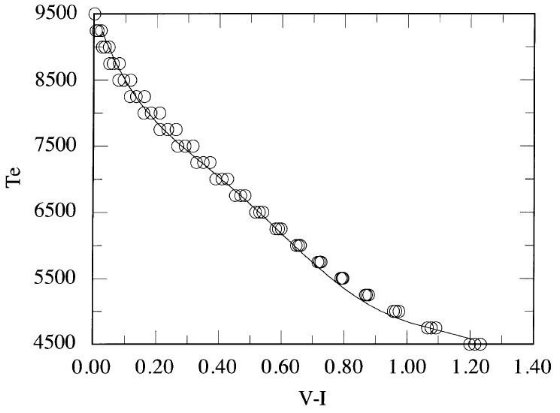
　V - I カラーは A - K 型星では温度に鋭敏でよいのだが、データが無い 標準星が多い。しかしそれらの b - y 値は揃っている。そこで、 Blackwell, Lynas-Gray 1994 と Alonso,Arribas,Marinez-Roger 1996 と Code et al 1976 星の b - y をHauck, Mermilliod 1990 から採り、次の式で V - I に変換した。

V - I = -0.00395 + 2.071846(b - y) - 1.09643(b - y)2 + 0.631039(b - y)3

この式は、Cousins 1976, 1987 による E-領域の 122 ２次標準星から得られた。

　Caldwell et al 1993 も UBVRIJHK と uvby との間の多項式関係を導いた。 このような表式は有用であるが、V-K で 10 等、V-I で 5 等の変化を考えると 一つの式で細かい変化まで表わすのには無理がある。この様な場合には幾つかの 小領域に区分して各領域で別の式を適用すべきである。いずれにせよ、このような 平均カラーの関係式で変換するよりは直接観測することが望ましい。



赤化の補正。ヒッパルコスへの期待　

　星のカラーを扱う際には赤化の影響を常に気をつけなければいけない。 一つの対処方法は、赤化フリーのカラー指数を用いることで、付録Ｆで述べる。
　もう一つはダストの分布マップ、Fitzgerald 1986, Burnstein, Hailes 1982 に星までの距離組み合わせて使うことである。

　しかし、一般に太陽から 100 pc 以内では赤化は無視できると考えられ、カラー カラー関係、カラー温度関係の較正に用いる星の大部分はこの範囲内にある。 実際、AAM96 の星はどれにも赤化が認められず、BLG94 の星の内 7 星のみが 0.02 等より大きい (V-K) 赤化を示す。

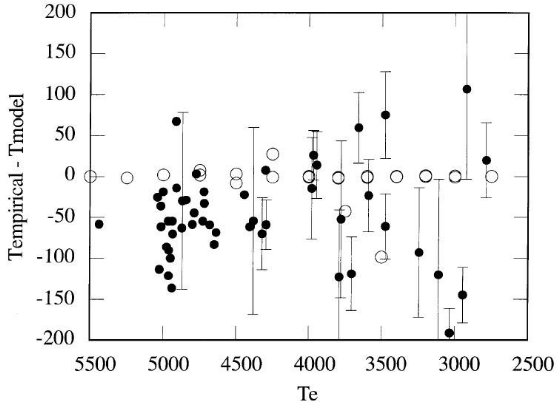
　0.02 ≤ E(V-K) ≤ 0.04 の 15 星に対し イエールとヒッパルコス視差 を較べると、ヒッパルコスは 6 星を引き寄せ、 5 星を遠ざけることが分かった。 Te とカラーのフィットからの残差を見て、新しい距離との相関を調べると赤化の 幾つかは過大に評価されているように見える。しかし、赤化自身が小さいので較正 式は殆ど変化しない。

　ヒッパルコス視差と Burnstein, Hailes 1982 マップ, 測光カタログ を組み合 わせると距離対赤化の以前よりずっとよいマップを作ることができる。それは、 より遠方の星に対しよりよい赤化補正を可能にするだろう。

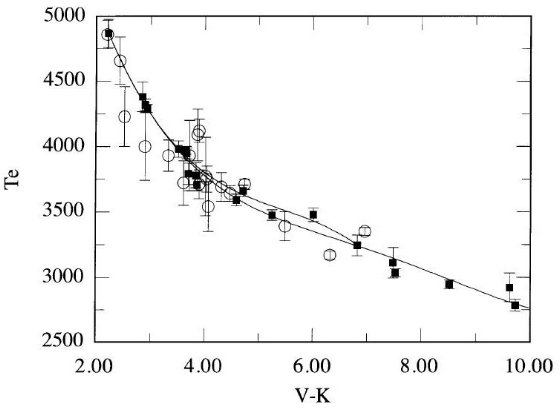
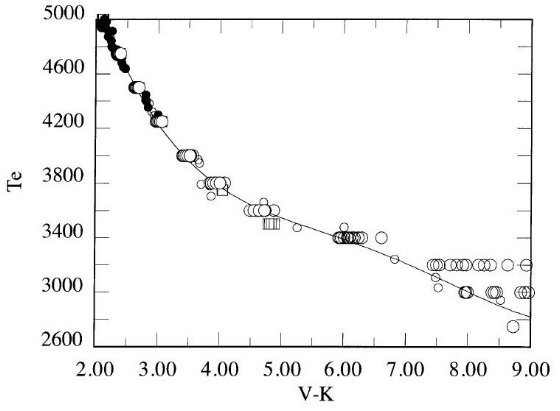
図１．巨星の Te 対 (V-K) 関係。白丸＝Ridgway et al 1980 月掩蔽。
　　　黒四角＝Ridgway et al 1980 の掩蔽、Di Benedetto, Rabbia 1987,
　　　Dyke et al. 1996, Perrin et al 1997 の干渉計データ



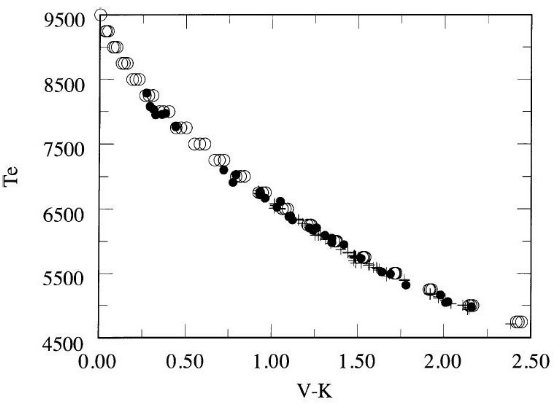
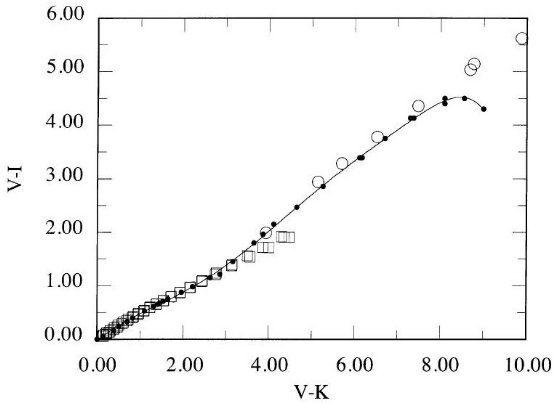
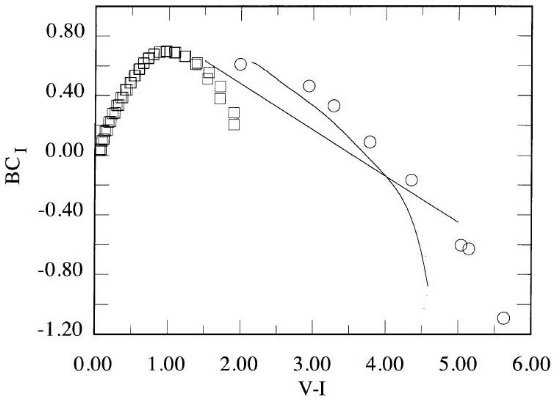
図２．矮星の Te 対 (V-I) 関係。とあるが図が変


経験的 Te 対 カラー　関係のまとめ　

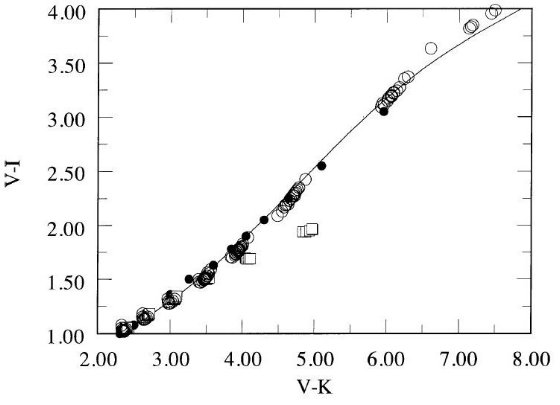
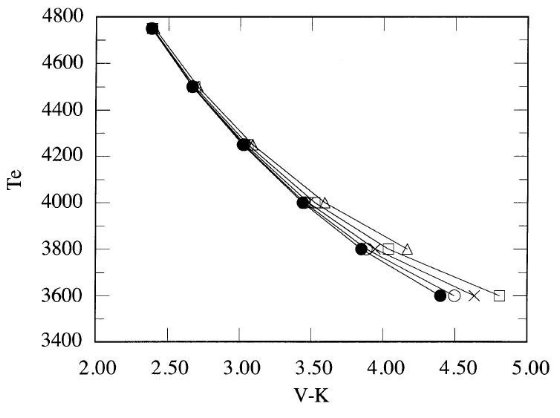
　図２には、BLG95 と AALM96(-0.02 ≤ [Fe/H] ≤ 0.02),の IRFM 温度に Code et al 1976 の干渉計法温度を足して、Te 対 (V-I) 関係を示した。 A - F 星に対し、IRFM データは強度干渉計より精度が高い。しかし、結果は 良い一致を示す。ただし、Code et al の最も熱い星 HR 7557 と IRFM データ には差がある。

　幸運なことに、A - M 型星の経験的温度平均スケールは Bessell 1979 から そう変わらなかった。しかし、過去６ 年の間に精度は大幅に向上した。最も 大きな変化はラインブランケッティングの入った現実的な大気モデルによる合成 カラーの計算と測光精度の向上である。

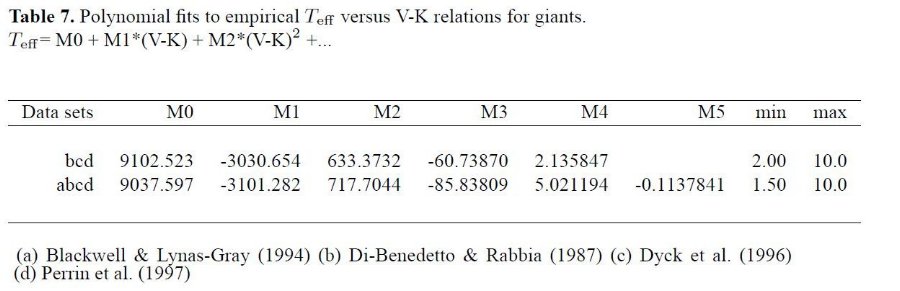
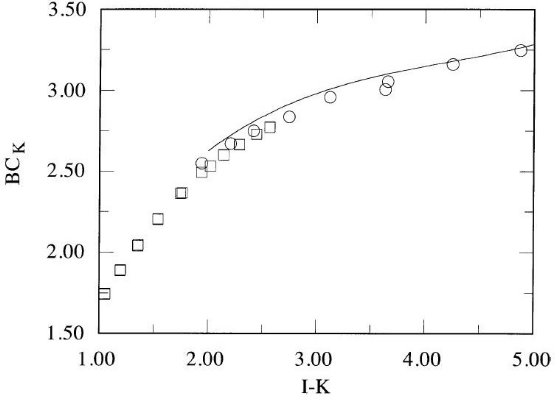
　表７には Te 対 (V-K) 多項式フィットの係数が載せてある。

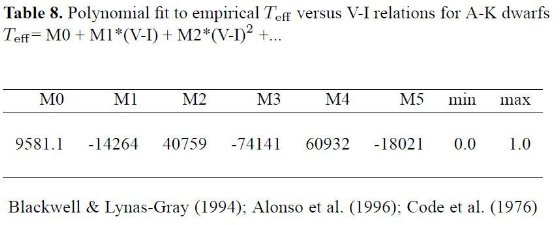
　表８は、 Te 対 (V-I) 多項式フィットの係数が載せてある。

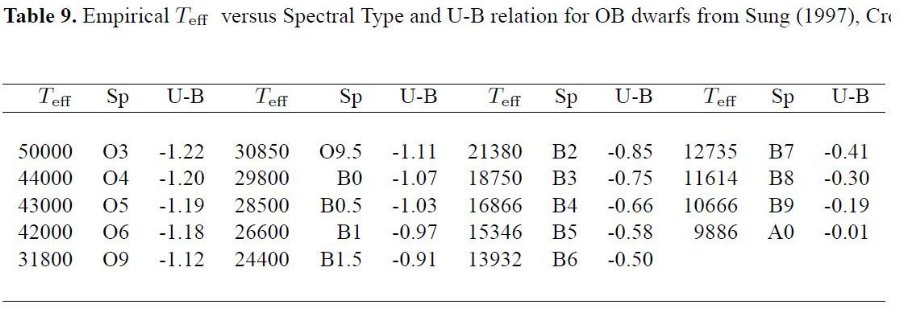
　表９は完全性のために、 O-, B- 型星の経験的温度スケールを Sung 1997 から 採ってきて載せた。



表７. Te 対 (V-K) 多項式フィットの係数


表８. Te 対 (V-I) 多項式フィットの係数


表９. O-, B- 型星の経験的温度スケール。 (Sung 1997 から)


　３．２．モデル大気と経験的温度・カラー関係の比較　

重力 - 温度関係　(モデル)　

　矮星の Te - (U-B), (V-K), (V-I) 関係と, 巨星の Te - (I-K) 関係を観測と 理論とで較べた。

　重力は次のように決めた。IRFM 較正に使った BLG94 と AAM96 の A-G 型星は 大部分がイエール視差カタログに載っている。従って、それらの光度と重力を 推定可能である。すると、ZAMS に乗る星は殆どなく、平均すると ZAMS の約 1 等上にあることが分かった。平均重力は 3.5 と 4 の間である。


図３(a)．Z = 0.02 (Schaller et al 1992)主系列モデル進化経路。質量(M๏)は、
　　　　　1(黒丸), 1.5(三角), 2.5(白丸), 5(バツ)


　温度と重力は理論的等時線(Bertelli et al 1994)や進化トラック(Schaller et al 1992, Charbonnel et al 1993) から得ることができる。

　図３(a), (b) には、太陽組成, M = 1, 1.5, 2.5, 5, 9, 15 M๏ の進化経路を Schaller 1992 から採ってきた。より低温側はBessell et al. 1991 で補った。他の組成も似たように描ける。太陽組成の星の重力は、巨星で log g = 3.0 ± 0.5 (Te = 5000 K),から、 = -0.2 ± 0.5 (Te = 3000 K) と広がる。ZAMS 星では、 O - late F 型で log g = 4.1 - 4.2 である。


図３(b)．Z = 0.02 (Schaller et al 1992 + Bessell et al 1991 拡張)巨星 モデル
　　　　　進化経路。質量(M๏)は、1(黒丸), 1.5(三角), 2.5(白丸), 5(バツ),
　　　　　9(ダイア), 15(プラス)

熱いO-, B-型矮星の温度 Te 対 カラー (U - B) 関係

　図４には、OB 型矮星の Te - (U-B) 関係をモデルと Crowther 1997 の観測温度 スケールとで示した。両者の一致は 30,000 K 以下では大変良い。しかし、 もっと熱い星では UBVRI 地上観測は最適と言えない。さらに UV 領域まで 入る観測は WPFC2 フィルターを付けた F160BW が最適である。


温かい(A-G型)矮星の温度Te 対 カラー(V - K), (V - I) 関係

　図５(a), (b) は A - G 型矮星の (V-K), (V-I) 対 Te 関係を観測とモデルで比較した。 モデルは オーバーシュートなしの ATLAS9 モデル、 log g = 3.5,4,4.5, である。 モデルはオーバーシュートモデルより少し青いので、観測への一致が良い。しかし、 それでもなおオーバーシュートなしモデルのカラー、(V-K), (V-I) は赤過ぎる。 この小さな差は、（１）ゼロ点を定めるのに使用したベガとシリウスのモデルと カラー、（２）モデルにまだ残る問題点、（３）パスバンドが合わない、のどれか が原因であろう。それにも拘らず、少しの調整で理論カラーは観測とよく合う。









図５ (a)．A-G 型矮星のTe-(V-K)関係。白丸＝ATLAS9(オーバシュートなし)。
　　　　　観測点はIRFM法による温度。シンボルは図２と同じ。

図４．OB 型矮星の(U-B)-Te関係。実線＝モデル大気。クロス＝観測。


図５ (b)．A-K 型矮星の Te - (V-I) 関係。実線＝観測点の多項式フィット。
　　　　　白丸＝ATLAS9モデル。左から log g = 3.5, 4.0, 4.5

冷たい(G-M型）矮星の温度 Te 対 カラー (V-I) 関係

　図６は G-M 型矮星の温度 Te 対 カラー (V-I) 関係である。G-, K-型矮星に 関しては IRFM 温度が得られるが、M-型矮星は二つの食連星, YY Gem, GM Dra しか半径が測られていない。YY Gem は古い円盤種族星で組成は太陽に近い。 GM Dra 高速度星だが大きなメタル欠乏度は示さない星である。Plez 1997 の NMARCS モデルはこの二つの温度スケールに良く合い、ATLAS9 に Te = 4250 K で 合流する。

　古いオパシティを用いた log g = 4.5 太陽組成グリッド Brett 1995a,b 表６ は (V-I) が 3800 K では 0.07 小さく、その差は 3000 K で 0.4 に増加し、 2400 K では 1.0 になる。



図６．G - M 型矮星 Te 対 (V-I) の観測とモデル比較。
　　　黒丸＝BLG94 IRFM 温度。プラス＝AAM96 IRMF 温度。　
　　　YY Gem, GM Dra は食連星。白丸＝NMARCS log g = 4.5 モデル。
　　　四角＝ ATLAS9(オーバーシュートなし)log g = 4.5, 4.0 モデル。
 　ATLAS9 オーバーシュートなしモデルは熱い矮星のカラーをよく再現する。 しかし、 Leung,Schneider 1978 は YY Gem の温度をここで得た Te より 300 K　 低い 3770 K とした。また、Chabrier,Baraffe 1995 は CM Dra の温度を 150 K 高い 3300 K としている。

M型矮星の温度 Te 対 カラー (I-K) 関係

　図７では M 型矮星 Te 対 (I-K) の観測とモデルを比較した。上の線は表２ のATLAS9モデル。下線は表６のNMARCSモデルである。YY Gem と CM Dra の他に 辻ら　1996a が求めた幾つかの M 型矮星の IRFM 温度を示した。Brett 1995a の遠赤スペクトラへのフィットラインも載せた。


図７．M 型矮星 Te 対 (I-K) の観測とモデル比較。
　　　エラー付き白丸＝YY Gem, GM Dra。クロス＝辻の IRFM Te
　　　黒丸＝Brett 1995a の遠赤フィット。
　　　上線＝表２のATLAS9モデル。下線＝表６のNMARCSモデル



GKM 型巨星の温度 Te 対 カラー (V-K) 関係

　図８では GKM 型巨星の温度 Te 対 カラー (V-K) 関係を示した。実線は 平均点へのフィットである。モデルのカラーは観測値に極めて良く合っている。 Te = 4000 - 3200 K では球対称性（大気の曲率）が重力と同程度か、それ以上に (V-K)カラーに影響する。しかし、3200 K 以下になると重力の影響が大きくなる。 古い円盤種族、M 型巨星では 3200 K 付近での重力は log g = 0.25 程度である。 超巨星では重力がもっと小さくなる。


図８．G - M 型巨星 Te 対 (V-K) の観測とモデル比較。
　　　黒丸＝ IRFM 温度。小白丸＝干渉計温度。
　　　四角＝ATLAS9オーバーシュートなし。log g = 0.0, 0.5, 1.0, 1.5 モデル
　　　大白丸＝NMARCS モデル。表4, 5 から。 		古い円盤種族巨星の温度 Te 対 カラー (V-K) 関係 の差

図９は古い円盤種族巨星の、観測(V-K)対観測温度関係とモデル(V-K)対 温度関係（太陽組成、1.5 M๏ 進化トラック）の差 をプロットしたものである。両者の一致はよい。

　Te = 5000 K 付近で少しずれるが。



図９．古い円盤種族巨星の観測温度とモデル温度の差。
　　　キャプションは横軸(V-K)と書いてある
　　　エラーバーのは干渉計。他はIRFM温度。白丸はATLAS9 とNMARCSの差

　３．３．モデルと観測的なカラー・カラー関係の比較　

　(J-K, V-K) 関係　

　図１０は Te ≤ 5000 K での (J-K, V-K) 関係を観測とモデルとで比較した ものである。上の線は近傍の巨星、下の線は矮星のものである。Te ≥ 4250 K (V-K ≤ 3.0) では ATLAS9 と NMARCS は一致し、観測ともよく合う。4000 K 以下(V-K ≥ 3.5)では NMARCS の方が観測に合う。

　H2O オパシティ と J-K カラー　

　ATLAS9 矮星モデル(黒四角)は H2O オパシティを欠いているので、 4250 K 以下では J-K カラーを合わせることができない。一方 NMARCS は全般的 傾向は良いのだが H2O バンドが強すぎる。

　Brett 1995a,b は H2O ラインリストに経験的平均オパシティを 統計的に扱ったものを使用した。Plez 1997 は Jorgensen 1996 の第１原理計算 からのラインリストを組み込んだが、それでも J-K 観測を良く合わせられな かった。現在進行中の NMARCS グリッドでは、 H2O オパシティを 非常に広範な Partridge,Schwenke 1997 ラインリストから組み込んでいる。 したがって、完全ではないだろうがよりよい一致を期待できる。

　 J-K カラーに寄与しているのは H2O が全てではないかも知れない。 その上、低温 M 型矮星のモデルはダスト吸収を必要とする。(辻 1996b)

図１０．(J-K, V-K) 関係を観測とモデルとで比較した。
　　　　線でつないだ黒丸は上が近傍の K0 - M7 巨星、
　　　　下が K2 - M7.5 矮星である(Bessell 1991)。
　　　　白四角はATLAS9オーバーシュートなしモデル(log g = 3.0 - 1.0)。
　　　　黒四角は同じく log g = 4.0, 4.5.
　　　　白丸はNMARCS巨星。黒丸はNMARCS矮星

　矮星の(V-I, V-K) 関係　

　図１１は矮星の(V-I, V-K) 関係が観測とモデルの良く一致することを示す。 もっとも、依然存在するラインオパシティの不確実性を考えるとこれは単なる 偶然の一致かも知れない。観測的 V-I カラーには存在する垂れ下りはモデルの 方には見当たらない。



図１１．矮星(V-I, V-K) 関係を観測とモデルとで比較した。
　　　　黒丸は太陽近傍の矮星の観測値。Bessell,Brett 1988,Bessell 1991
　　　　四角はATLAS9 モデル。白丸はPlez 1997 NMARCS モデル。 		　巨星の(V-I, V-K) 関係　　

　図１２は Te ≤ 4000 K の M 型巨星の(V-I, V-K) 関係が観測とモデルで 良く一致することを示す。

　元の二つの NMARCS グリッドではどちらも不一致が大きかった。古いオパシティ を使っていたので、 V-K = 7 付近では V-I カラーがまるまる１等ほど青過ぎる 結果になった。


図１２．巨星(V-I, V-K) 関係を観測とモデルとで比較した。
　　　　黒丸は太陽近傍の巨星の観測値。Bessell,Brett 1988
　　　　実線は Caldwell et al 1993
　　　　四角はATLAS9 モデル。白丸はPlez 1997 NMARCS モデル。

　(B-V, V-I) 関係 　

　(B-V) は特に低温度星でモデルと観測の一致が良くない量である。図１３と 図１４には矮星と巨星の(B-V, V-I) 関係を示した。A - G 型星に関しては 一致はまあ良い。それでも A - F 型星のモデル(B-V)は少し赤過ぎる。

　M 型矮星では一致は悪く、モデルカラーは 0.2 - 0.8 等青すぎる。巨星に 関しては、NMARCS モデルは Te = 4750 K で１００分の数等青いが、3600 K では それが 0.2 等に達する。



図１３．矮星の(B-V, V-I) 関係。実線はCaldwell et al 1993 観測値。
　　　　四角＝ATLAS9(表２)。黒丸＝NMARCS Brett1995(表６メタル量３種)。
　　　　白丸＝Plez 1997 太陽組成 		　青ーＵＶ領域オパシティの改善　 この原因の一部はフィールド星のメタル量に広がりがあるためである。しかし、 主には青とＵＶでのオパシティの不備にある。
　NMACS は新しいオパシティの導入により V バンドフラックスが著しく改善さ れた。より短波長側のオパシティの検査はまだ済んでいない。最終的な NMARCS グリッドは VALD (Piskunov et al 1995) からの原子ラインデータとKurucz デ ータからの補充を含むだろう。現在の NMARCS モデルは古い Kurucz 1989 テープ しか使っていない。多くの分子が青-ＵＶ領域に電子遷移を有していることを注意 しておく。


図１４．巨星の(B-V, V-I) 関係。実線は Bessell,Brett 1988 G0-M2観測値
　　　　四角＝ATLAS9(表２)。(Te,log g) = (3500,0.5), (3760,1.0), (4000,1.5),
　　　　(4250,2.0), (4500,2.5), (4750,3.0), (5000,3.5), (5750,3.5), (5500,4.0)
　　　　白丸＝NMARCS (表4,5)。
　　　　(Te,log g) = (3600,0.5), (3800,1.0), (4000,1.5),(4250,2.0),(4500,2.5),
　　　　( (4750,3.0)

　３．４．K-, M-巨星のカラー指数に対するメタル量の影響　

　この節では K-, M-巨星の(B-V), (V-I), (J-K), (V-K) カラーに及ぼすメタル 量の影響について述べる。扱ったメタル量は銀河系中心、古い、若い円盤種族、 マゼラン雲の範囲を含む。温度と重力の組み合わせは太陽組成、古い円盤種族 巨星に相当し、他の組成でも同じパラメターを使用した。したがって、他の組成に 対しては必ずしも巨星枝に沿った温度ー重力を表わしていない。

K-, M-巨星の理論的 Te - (B-V) 関係　


図１５．K-, M-巨星の理論的 Te - (B-V) 関係。NMARCS パラメターは、
　　　　(Te,log g) = (3600,0.5), (3800,1.0), (4000,1.5),(4250,2.0),(4500,2.5),
　　　　　　　　　　　　(4750,3.0)
　　　　[M/Fe] = -0.6, -0.3, 0, 0.3, 0.6



　(B-V), (V-I), (V-K) に対しては、低メタルは青いカラーを意味する。例外は Te < 3900 K での B-V である。逆は J-K で低メタルになると赤くなる。 V-K はメタルの影響が最も小さく、Te > 4000 K ではメタル不変と言ってよい。



　K-, M-巨星の理論的 Te - (V-I) 関係。


図１６．K-, M-巨星の理論的 Te - (V-I) 関係。モデルは図１５に同じ。

　K-, M-巨星の理論的 Te - (V-K) 関係　


図１７．K-, M-巨星の理論的 Te - (V-K) 関係。モデルは図１５に同じ。 		　K-, M-巨星の理論的 Te - (J-K) 関係　


図１８．K-, M-巨星の理論的 Te - (J-K) 関係。モデルは図１５に同じ。

　３．５．(V-I,BCI), (I-K, BCK)関係　


図１９(a) A - M 型矮星の BCI 対 (V-I)。直線は Reid,Gilmore 1984
　　　　　の関係。曲線は Tinney et al 1993。四角はATLAS9 log g =4.5(表２)
　　　　　白丸は Plez 1997 の NMARCS (表６)




　図１９(a),(b) は矮星の輻射補正 BCI, BCK の観測値 とモデル値を示す。BCI は非常に低温で (V-I) が赤過ぎる星を除くと、 観測とモデルの一致が良い。BCK は非常に良く合っている。

　モデルとTinney et al 1993 との間には僅かなずれがある。この原因として、 ベガ、シリウスのフラックスとして両者が異なる値を採用していたこと、モデル の未解決問題等が考えられる。最も低温度の星で見られる小さな差は観測エラー とモデル不確定性の範囲内である。NMARCS （表５) は異なるメタル量に対して 実質的には同じ BCK を与えている。


図１９(b)A - M 型矮星の BCK 対 (I-K)。曲線は Tinney et al 1993
　　　　　四角はATLAS9 log g =4.5(表２)。白丸は Plez 1997 NMARCS (表６)



図２０．K-, M-型巨星の BCK 対 (V-K)。実線は Bessell,Wood 1984
　　　　黒丸はFrogel et al 1981. 四角は ATLAS9(表２),白丸はNMARCS表4,5

　４．結論　

　カラー温度関係の採点　

　新しい大気モデルのカラーと輻射補正値を、太陽近傍星から観測的に得た 関係と較べた。大部分のカラーで一致は良かった。カラー - Te 関係は、 U-B が B0 - A0 矮星、V-K が A - G 型矮星、V-I が A - M 型矮星、 I-K が M 型矮星、V-K が G - M 型巨星 が特によく合った。輻射補正に 関しては、矮星の (V-I) - BCI, (I-K) - BCK, 巨星の (V-K) - BCK 関係が良く合った。

　例外は、NMARCS モデルでは、K 型巨星、M 型巨星、M 型矮星の (B-V)、 M 型矮星 2800 K 付近での (J-K)である。これらの問題点は今後の課題だが、 冷たい星の IR に関してはほぼ確実に H2O ラインの不足による ものである。2500 K 以下ではダストの影響を考慮しなければいけない。

　Chabrier et al 1996 による主系列底部での M - L 関係の導出も重要である。

　可視域でのオパシティの不備　

　モデルの(B-V) が落ちる原因はほぼ確実に青 - 実視領域でのオパシティの不備 である。現在の NMRCS モデルはFe族元素に関し、Kurucz 1991 の原子線リストを 用いている。原子線以外に、分子線も必要な可能性がある。我々が TiO a-f システムをモデルに入れた結果は無視できない効果があった。新しいラインリスト は今後大きな改善に導くだろう。

　低温度星のカラー　

　3000 K 以下では大抵の星は変光星となり、ショック波が非常に広がった大気を 形成する。この論文で扱う静的なモデル大気はこの様な低温巨星を表現できない だろう。この様な大気の試験的な探求が Bessell 1989, 1991, 1996, Hofner, Dorfi 1997 により試みられた。Bessell et al 1991 は AGB 進化経路を 2500 K まで 追った。カラーと光度がそこでは示されている。しかし、ラインオパシティの 欠如のためカラーの幾つかは信用できない。モデルの構造はそう大きく影響され ないと考えている。 		　ミラのモデル　

　Alvarez, Plez 1997 は NMARCS ラインオパシティを使ってミラの現実的な モデルを作った。Scholz, Takeda 1987 はミラのように広がった大気を持つ星の 半径測定に伴う複雑さを論じた。

　ATLAS9 と NMARCS モデルの比較　

　ATLAS9 モデルは 4250 K より熱い星のカラーは全てよく再現する。 矮星 4200 K 以下,　巨星 4000 K 以下では NMARCS モデルの方が分子オパシ ティが完備しており優れている。巨星の...（ここは 意味が通らない）

　Gustagsson et al 1975 モデルも 4500 K 以下では不十分である。4300 K 以下 の星に観測カラーとRidgway et al 1980 カラースケールを適用してモデルパラ メターを決めると系統的にメタル量が低く出過ぎる。NMARCS モデルで、Bessell, Plez 1997 は M67, 47 Tuc の巨星枝に沿ってメタル量の系統的なずれを認めな かった。V-K と V-I カラーには Te = 4000 - 6000 K で、重力効果が殆どない。 3600 K 以下になると低重力モデルは非常に赤くなり、拡がった（低質量）モデル は少し赤くなる。（文章のつながりが？）

　カラーから温度決定の道筋が出来た　

　上のような比較に基づき、組成、光度、質量の異なる星のカラーは、全て の質量と年齢を持つ星の温度が導かれることを可能にすると期待できる。 。（ここも、特に"enable equally as reliable temperature" の意味がはっきりしないけど。）　さらに銀河や星団の合成積分カラー が計算できるようになることも期待できる。

　付録Ａ：測光システムのゼロ点　


　Ａ０．ベガとシリウス　

　UBVRIJHKL システムのゼロ点は伝統的にベガや A0 星の等級とカラーから決め てきた。しかし、ベガは南半球から観測できないため、Cousins(UBVRI) と　Glass, Carter(JHKL) 精密測光カタログに入っていない。また、変光の疑いがあり、赤外 超過が発見された。そこで、シリウスを基本測光標準星に追加した。(Cohen et al 1992)

　この論文ではベガとシリウスの ATLAS モデルから得た等級をゼロ点 と定めた。採用したモデルは、(Te, log g, Z, vmicro) = (9550 K, 3.95, -0.5, 2 km/s) Castelli, Kurucz 1994 と (9850 K, 4.25, +0.5, 2 km/s) Kurucz 1997である。

　Ａ１．Ｖのゼロ点　

　Castelli, Kurucz 1994 のベガモデルを使って、モデルフラックスからＶ等級 への変換を次のように決めた。

V = -2.5 log ∫f(λ)Rv(λ)dλ -21.100
∫Rv(λ)dλ


V = -2.5 log ∫f(ν)Rv(ν)dν -48.598
∫Rv(ν)dν


　フラックスの単位は、f(λ) が erg cm-2s-1A-1, f(ν) が erg cm-2s-1Hz-1, R はバンドの 応答関数で Bessell 1990 から採った。この式ではベガは V = 0.03 となる。

　ベガの 5556 A におけるモデルフラックスと観測値 (Hayes et al 1985) は 良く合い、角直径（Code et al 1976）も１σ エラーの範囲で一致する。 ベガの場合、観測値 qd ＝ 3.24 ± 0.07 mas, モデルは 3.26 mas で、シリウスでは、観測値 qd ＝ 5.89 ± 0.16 mas, モデルは 6.04 mas であった。

　Ａ２．カラー指数のゼロ点　

　ベガとシリウスのモデルと観測の差　

　(U-B), (B-V), (V-R), (V-I) のゼロ点を決めるため、ベガとシリウスの観測 とモデルとのカラー差を平均した。(V-J), (V-H), (V-K), (V-L) のゼロ点は シリウスの観測カラーをフィットして決めた。

　表Ａ１にはシリウスとベガの観測、モデルカラーを載せた。一般には両者は 素晴らしく良く合う。ベガの V-K だけは差が少し大きいが１σ エラー 内である。

　シリウスの赤外カラー　

　シリウスの赤外等級は Carter 1990 が SAAO システムで測った。SAAO システムのゼロ点は B1 と A7 の 25 主系列星観測から決めた。K ゼロ点は その 25 星の (V-K, B-V) が V-K = 0, B-V = 0 を通ることを確認して決めた。 Carter 1990 には SAAO システムに相対的に ESO, CTIO, AAO, MSSSO システム のゼロ点とカラータームが与えられている。

　ベガの赤外超過はない　

　ベガの赤外超過については Leggett et al 1986 が　B8 - A3 の 25 矮星の 1 - 5 μm 狭帯測光を行い、ベガが他の A 型星に対してはエクセスを持た ないことを確認した。

　ベガの絶対フラックス較正　

　しかし、Mountain et al 1985, Blackwell et al 1983, Selby et al 1983 によるベガの赤外絶対フラックス較正は、Dreiling, Bell 1980, Krucz 1979 のモデルに対して 2 - 5 μm で超過を持つことを示した。Leggett et al 1986 はこれをモデルにエラーがあるためと解釈したが、A 型星で支配的な H オパシ ティに誤りが残されているとは考えにくい。絶対フラックス測定の際の減光 補正に問題があったのではないか。

　いずれにせよ、問題が解決されるまでモデル大気のフラックスの方を絶対 フラックス測定よりも優先して使用することを薦める。Cohen et al 1992 も参考にせよ。



表Ａ１ シリウスとベガの観測、モデルカラー



　付録Ｂ：UBVRIJHKL システムのゼロ点フラックス　

　表Ａ２には、全てのバンドで０等の仮想的 A0 星に対するフラックスを与えた。 これはベガを V = 0.03 として導かれた結果である。

　付録Ｃ：太陽および太陽類似天体のカラー　

　太陽のＶ等級　

　太陽もしばしばフラックス較正に用いられる。Stebbins,Kron 1957 の測定に 最近の G 型矮星データを比較に用いて V = -26.744 ± 0.015 が得ら れる。Hayes et al 1985 は更に水平減光の補正を加え、 V = -26.76 ± 0.02 を主張している。 		　太陽と太陽類似天体のカラー　

　Colina et al 1996 は、Neckel, Labs 1984 の太陽の分光測光観測データに 他波長データを結合して 0.12 μm - 2.4 μm のフラックススペクトルを 作成した。我々はこのスペクトルを計算して等級とカラーを算出した。（表Ａ３）

　Cayrel de Strobel 1996 は太陽類似天体の水素線プロファイルを較べ 温度、重力、組成を導いた。表Ａ３にはその候補星の U-B, B-V カラーを 載せた。

　われわれは ATLAS9 でオーバーシューティングを "ON" と "OFF" の両方で 太陽モデルを計算した。

　一般に太陽類似天体の観測とモデルカラーの一致は良い。例外は U-B と V-I である。太陽に対しては, V = -26.76 を採用する。これは距離指数 = -31.57 から Mv = 4.81 に相当する。


　　　　　　　表Ａ２　UBVRIJHKL の有効波長(A0星に対し）、ゼロ等フラックス、 ゼロポイント等級



　　　　　　　表Ａ３　太陽、太陽類似天体の等級とカラー（観測とモデル）

　付録Ｄ：輻射補正および輻射等級のゼロ点　

　輻射補正と輻射等級の定義

　輻射等級の定義は、

　　　　　mbol = -2.5 log (fbol) + constant

　　　　　mbol = -2.5 log (∫fλdλ) + constant

ここに、fbol)は大気圏外で天体から受ける総フラックスである。

　輻射補正は、

　　　　　mbol = mV + BCV

で定義される。当初、輻射補正が使われたのはＶ等級のみであったが、現在では 全てのバンドで用いられるようになった。

　輻射補正のゼロ点の混乱　

　伝統的に、Ｖバンドでの輻射補正が全ての星でマイナスであるべきだという 了解があり、その結果Ｆ型矮星付近で輻射補正をゼロとし太陽の輻射補正は -0.07(Morton, Adams 1968) と -0.11 (Aller 1963) の間になった。 全バンドに輻射補正が導入された時点で全ての星で輻射補正がマイナスという 要求は根拠を失ってしまったが。

　Kurica 1979 はこの伝統を定式化し、彼の BCV ゼロ点を、 (Te = 7000, log g = 1.0) モデルに置いた。このモデルが彼のグリッド中で 最小の BC を示したからである。この結果太陽モデルは BCV = -0.194 となった。この大気モデルに基づくゼロ点は Schmidt-Kaler 1982 に採用され、 彼らは太陽に対し、 BCV = -0.19 とした。

　問題は、出所を明らかにしない異なるゼロ点に基づく輻射補正が文献中で使用 されていることである。Cayrel 1997 が強調するように、ゼロ点の歴史的基盤は もはや失われており、太陽の観測に基づいたゼロ点を採用すべきであろう。

　太陽の輻射補正　

　太陽定数は、Duncan et al 1980 によると、
　　　　　 f๏ tot = 1.371 × 106 erg cm-2 s-1 = 1371 W m-2 s-1
従って、 L๏ = 3.855 × 1033 erg s-1, 　　　　　(総光度)
　　　　　　F๏ = 6.334 × 1033 erg cm-2 s-1　　(表面フラックス）
　　　　　　Te = (F๏/σ)1/4 = 5871 K

　太陽の絶対輻射等級を　Mbol ๏ = 4.74 としよう。

　太陽の観測された見かけ V 等級 V ๏ = -26.76 から、太陽の 絶対 V 等級は Mv = 4.81 である。したがって、太陽の輻射補正は、
　　　　　　BCv = 4.74 - 4.81 = -0.07
である。

 　星の輻射補正　

　一般の星の輻射等級は以下の式で求められる。
　　　　　　Mbol = 4.74 - 2.5 log (L/L ๏)
　　　　　　　　　　= 4.74 - 2.5 log [(Te4R2)/ (Te๏4R๏2)]

　計算された V 等級（計算法はＡ１）は下式で絶対等級 Mv に変換される。
　　　　　Mv = V - 2.5 log (R2/D102)
ここに、D10は 10 pc である。

　輻射補正は、

　BCv = 4.74 - V - 2.5 log (Te4) + 2.5 log(D10 2) +2.5 log(Te๏4R๏ 2)

そして、最終的に、

　BCv = -V - 2.5 log (Te4) -0.8737

この表式は我々のモデルの輻射補正を決めるのに用いられる。
合成モデル絶対等級 MV ๏ = 4.802 を用いると、太陽の 輻射補正は、BCv = 4.74 - 4.82 = -0.062 となる。この値は、前に決めた 値 -0.07 と非常に近い。将来の改良された太陽モデルが V 等級を変化させて も我々はモデル輻射補正 -0.062 に依存せず、採用した太陽の絶対輻射等級 Mbol = 4.74 と 観測値 Mv = 4.81 を維持していく。表Ａ３ を見ると分かるが、ここに採用した V 等級の値は観測太陽スペクトルから計算 した値と、モデルスペクトルからの値の中間である。

表Ａ４には太陽パラメターをまとめ、幾つか文献からの値も併記した。

しかし、上の式はめちゃめちゃなように見える。

　　　　　Mv = V - 2.5 log (R2/D102)

の R は距離 D が入るべきであるし、その下の式もおかしい。

mbol = 4.74 - 2.5 log (L/L ๏) + 2.5 log (D2/D102)
　　　= 4.74 - 2.5 log [(Te4R2)/ (Te๏4R๏2)] + 2.5 log (D2/D102)
なので、
BC = mbol - V に代入すると、
　BCv = 4.74 - V - 2.5 log (Te4) + 2.5 log(D2/ R2) +2.5 log(Te๏4R๏ 2/D102)

で上の式と違う。大体あの式は次元が狂っている。

　　　　　　　表Ａ４　太陽のＶ等級と輻射補正（観測とモデル）

　付録Ｅ　標準システム等級・カラーを理論的に作る。


　付録Ｆ　有効波長と赤化比。