| 球状星団の赤色及び黄色変光星の周期・光度・カラー関係を調べた。その結果、 高温で、低メタルの星団変光星は基本振動であることが判った。 | 一方、低温で高メタルの変光星は第倍音振動をしている。それが正しいと仮定して、 基本振動周期と輻射等級を P = 1 - 300 d の間で導いた。 |
|
球状星団セミレギュラー RR Lyr, Cepheid 変光星に比べミラの理論、観測的研究は進んでいない。黄色、 赤色セミレギュラーでは状況はさらに悪い。脈動理論でこれ等の星の観測結果を 検討する研究としては、ウッド 1980, フォックス 1982, フロゲル 1983 くらい しかない。この論文の目的は、球状星団セミレギュラー (P = 30 - 180 d) の 周期・光度関係と脈動特性を調べることである。これらセミレギュラーの、より 良く調べられている、より長周期のミラ、より短周期の種族 II セファイドとの 関係も調べる。 周期・光度関係 Russev 1975, Rosino 1978 はある種の周期・光度関係が球状星団変光星に あるという示唆をした。 Menzies, Whitelock (1985) は JHKL データから求めた放射等級を用いて、球状星団ミラ型星の周期光度関係 を明らかにした。Harris 1981 は種族 II セファイドの 周期・V等級関係を示 した。周期光度関係を広範な波長域での測光を基に調べられるようになったのは 最近である。 |
分類 P > 30 d の球状星団変光星は次の3種に分類される。 (1)ミラ型星。高メタル星団。(Frogel, Persson, Cohen 1981) (2)Frogel 1985b が "特異" と名付けた変光星。SRd 型変光星 (Feast 1980). ミラよりは暗い。ヘリウムフラッシュ後の青方向ループ進化か、post-AGB で 白色矮星に向かう途中かではないか? (3)AGB か RGB か不明だが、巨星枝先端付近。 Frogel 1985b はミラと”特異”型変光星は赤外超過を示すことを発見した。 赤色巨星枝カラーとメタル量 Frogel, Cohen, Persson 1983 は赤外観測から、色等級図上で球状星団赤色 巨星の位置が Zinn 1980 の [Fe/H] と良い相関を持つことを示した。 |


2.1.周期表1のデータは特にコメントしていない限り、Sawyer Hogg 1973 から採った。 観測回数が少ないため、または規則性が低いために周期が怪しいものもある。2.2.輻射等級見かけ輻射等級見かけ輻射等級は JHKL データから Robertson 1980, Menzies, Whitelock (1985) の手法で求めた。短周期で (J-K)o ≤ 0.9 の暖かい星の場合、観測回数の 不足と、振幅が比較的大きいことから、輻射等級の不定性が大きい。エラーは 冷たい星で 0.2 等よりやや小さく、暖かい星でやや大きい。水蒸気吸収帯の 影響は補正していないので、分子吸収の大きい星では輻射等級が少し明るい だろうが、 その効果は 0.1 等を下回る。 星団距離 Sandage (1982a), Sandage (1982b) は球状星団 RR Lyr の絶対光度とメタル量の関係を調べた。しかし、 Feast 1984 は ⟨Mv(RR)⟩ = +0.6 とすると、様々な方法で決めた LMC 距離 との一致が良くなることを示した。そこで、この ⟨Mv(RR)⟩ = +0.6 に基づく星団距離を採用する。ただし、この仮定は自明ではないので、この先 必要な個所では RR Lyr 絶対光度にメタル量効果がある場合の変更については 触れる。 ⟨Mv(RR)⟩ - [Fe/H] 関係は Sandage 1982a,b と Lub の 二つがある。二つは勾配が同じでゼロ点だけが異なる。今回重要なのは勾配な ので、どちらでも結果にはあまり影響しない。Feast 1984 は Sangade の関係 を使うと、 LMC 距離が他の方法で求めた値と大きくずれることを示した。 そこで、ここでは Lub 関係を使用する。 |
2.3.有効温度Ridgeway スケール低温度星の有効温度は未だに確定していない。そしてそれはミラ型変光星の 脈動モードの不定性に直結している。 Ridgeway, Joyce, White, Wing (1980) は月の掩蔽を用いて、K0 - M6 のフィールド巨星の掩蔽温度を決めた。それらは 大気モデルの計算と合い、正常な=高メタル、低分子吸収、星の温度として妥当 に思える。この温度スケールを (J-K)o の関数として表した、 Bessell, Wood, Lloyd Evans 1983 の結果を、ミラ以外の変光星に対して使用する。ミラ型星に 関し、少なくとも P = 200 - 400 d の範囲では、 Robertson, Feast (1980), Glass, Feast 1982 は黒体フィット温度が月掩蔽温度とよく一致することを 示した。黒体温度と輻射等級は Robertson 1980 にある。 分子吸収の影響 Ridgeway 温度スケールを採用すると、ミラではないが振幅の大きな ω Cen V17 では TiO 吸収のために温度を高く見積もる。一方、ミラ型星 47 Tuc V4, V7 と ω V6 では黒体フィットをすると低温に見積もる結果となる。 それらの欠陥はあるが、我々はこの方式が可能な最善策と考える。注意すると 低メタル星には温度スケールが存在しない。それで高メタル星の温度スケールを そのまま適用した。表1にその結果を示す。 |
|
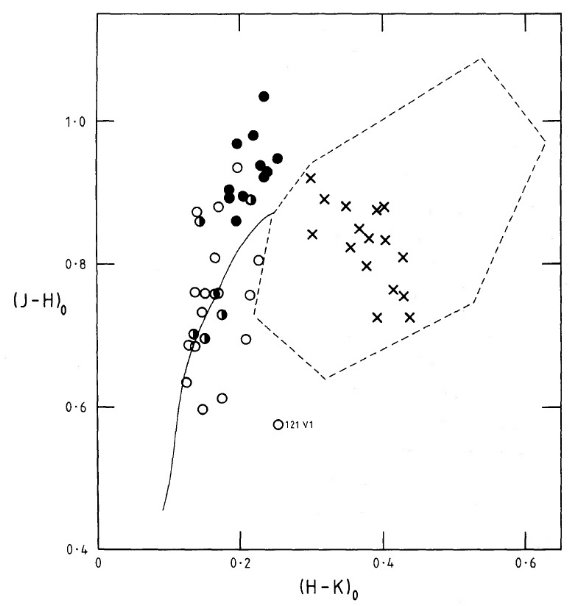
メタル量で2分 図1は星団変光星の2色図である。可能な限り、極大と極小の平均カラーを 示した。図を見ると、[Fe/H] > -0.7 の高メタル群と [Fe/H] < -1.1 の低メタル群にはっきり分かれる。メタル量に幅があることで有名な ω Cen の変光星もはっきり二分されている。 ミラ区域 ミラ的変光星はフィールドミラと同じ領域内に固まっていることが判る。 これは強い水蒸気吸収の影響である。 図1.星団変光星の赤外二色図。黒丸= [Fe/H]>-0.7 の高メタル星団星。 白丸= [Fe/H]<-1.1 の低メタル星団星。反黒丸= ω Cen 星。 バツ=ミラ型又はミラ的な星。通常星の経路とフィールド星のミラ型枠 (Feast et al 1982) も示す。 |
 |
|
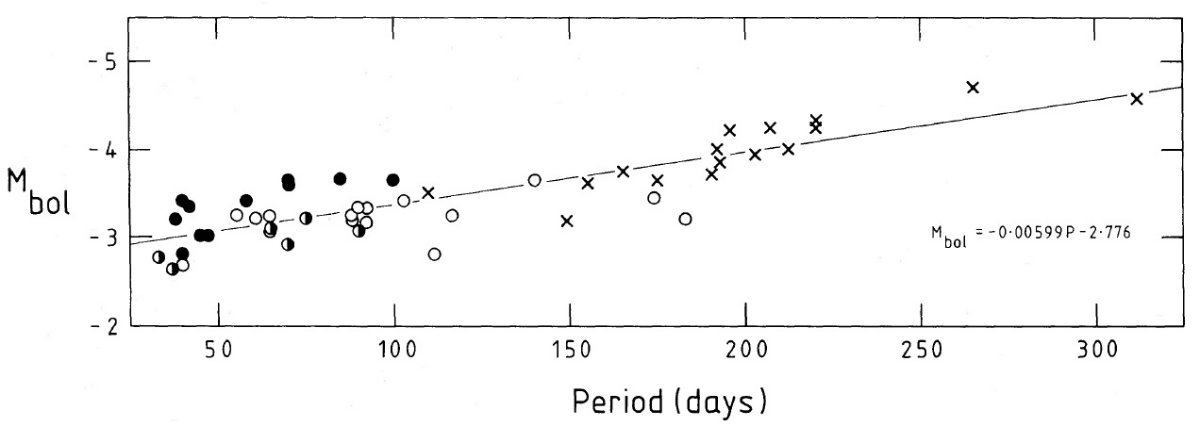
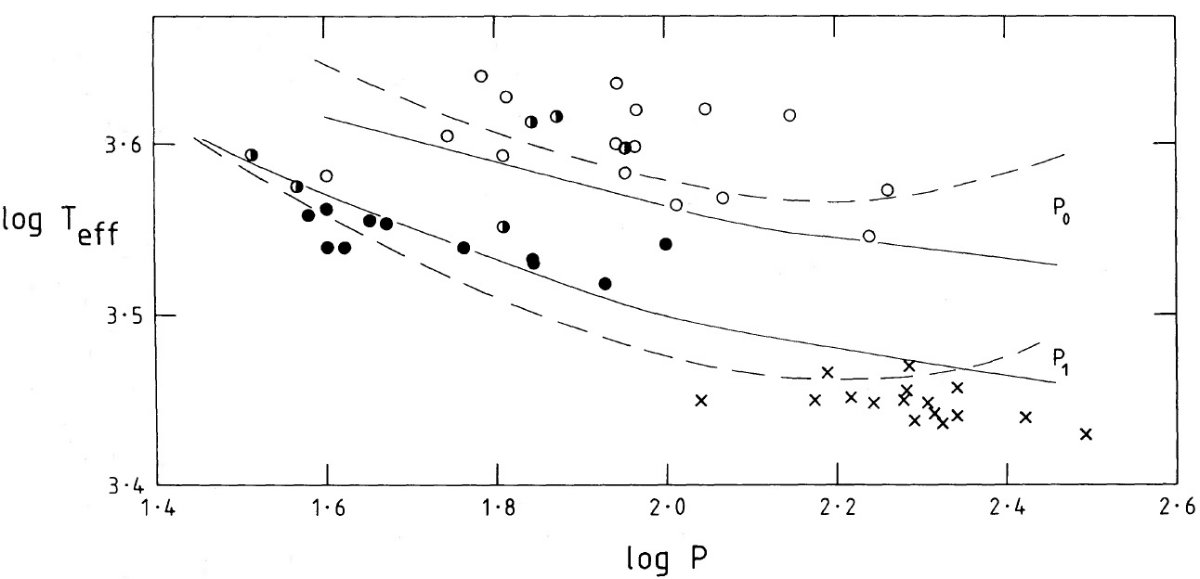
メタル量による分離 図2は星団変光星の周期と光度の関係を示す。高メタル星がフィット線の 上に、低メタル星は下側に位置する傾向がある。図3の周期・温度関係では 低メタル星と高メタル星ははっきりと分かれる。同じ周期で較べると、低メタ ル星の方が高温である。 図3=振動モードの分離 図3の二本の点線は基本振動 P0 と 第1倍音振動 P1 に対するモデル曲線である。この導出は以下のようである。図2のフィットは Mbol = -0.006 P - 2.78 Glass, Feast 1982 の脈動方程式は、 log(QM-1/2) = logP + 0.3Mbol + 3logT eff - 12.71 (1) 質量 0.65 Mo 脈動定数 Q は Fox, Wood 1982 から採った。Teff の 不定性は大きいが、それでも低メタル星団の変光星が基本振動ラインに、一方 高メタル星団星が倍音ラインに乗ることが判る。ω Cen の星は分かれる。 二分化の原因は他に何が? では、振動モード以外に何がこの二分化の原因となり得るだろう? (1)温度のエラーで分かれる 星団巨星枝の温度がメタル量で分かれることは理論的、観測的に確立している。 また、Ridgeway 温度スケールの星は巨星枝の近くにある。したがって、低メタ ルと高メタルの変光星を近づけるような温度補正は、同時に巨星枝を近づける ことになるので、ありそうにない。 (2)質量差 二つのグループ間に質量差があるという説はどうだろう。Iben, Renzini 1984 によると、ターンオフ質量は次の式で表される。 logMRG = (0.006log2Z + 0.040logZ + 0.038Y - 0.251) logt9 + 0.634 + 0.014log2Z + 0.100logZ - 0.799Y (2) ヘリウム量 Y = 0.25 と仮定し、Carney 1980 のメタル量時間変化 t9 = -5.1 [Fe/H] + 8.1 を上式に代入すると、 Z = 0.00017, すなわち [Fe/H] = -2, に対し、t9 = 18.3, MRG = 0.74 Mo Z = 0.017, すなわち [Fe/H] = 0, に対し、t9 = 8.1, MRG = 1.08 Mo となる。 (主系列進化時間、メタル量変化の新しい 表式を入手する必要がある。どこか? ) |
事前のマスロス 比較的低メタルの星団がセファイドを持ち、 Gingold 1976 の進化経路と較 べるとその質量は 0.55 - 0.6 Mo である。これは 0.2 Mo 程度の質量損失が 赤色巨星枝または早期 AGB 期にあったことを意味する。質量放出率は高メタル の方が大きいだろうから、高メタル星団の変光星も 0.2 Mo の質量損失を受けて いると考える。高メタル星はセファイドを作り出すほどの量の質量損失をしてい ないので、0.8 Mo AGB 質量に対応する明るい AGB 先端部を持つのである。 簡単に言うと、星団変光星の間の質量差が最大なのは、高メタル星団第1赤色 巨星枝にある高メタル変光星 1 Mo と低メタル星団の AGB を離れる寸前の 0.5 Mo で、質量比では 2 に相当する。 (第1赤色巨星枝上の変光星って CMDで確認できるのか? 何ていう星だ?) 質量比の影響 前の式 (1) から ΔlogM = ΔlogTeff であるから、 質量で4倍の変化が loglogTeff で 0.1 の変化に当たる。これ では図3の Teff の差を説明するには足りない。 図4=仮想基本振動周期光度関係 以上から、図3の解釈としては、高温、低メタル変光星が基本振動で、低温、 高メタル星は第1倍音振動と看做すのが妥当である。 Fox, Wood 1982 は P > 50 d の低質量星では、基本振動周期と第1倍音周期の比がほぼ 2 である ことを示した。それで、図3から、倍音と看做される星の周期を2倍にして、 仮想基本振動にした周期光度関係を図4に示す。その直線フィットは、 Mbol = -1.33 log P0 - 0.56 である。 統合周期光度関係 星団セファイドと RV Tau は基本振動と考えられているので、 Harris 1985 の 周期をそのまま用いた。こうして、星団変光星に関しては周期が 1 日より長い 全ての変光星を一本の周期光度関係にまとめることが出来た。ミラだけの場合 には、 Menzies, Whitelock (1985) が示すように、もう少し急で LMC ミラと共通の勾配を示す。ただ、レフェリーの 指摘にあったように、脈動定数はセファイドと赤色変光星とでは基本モード だとしても異なる。したがって、図4はあくまでも観測事実として考えるべきである。 |
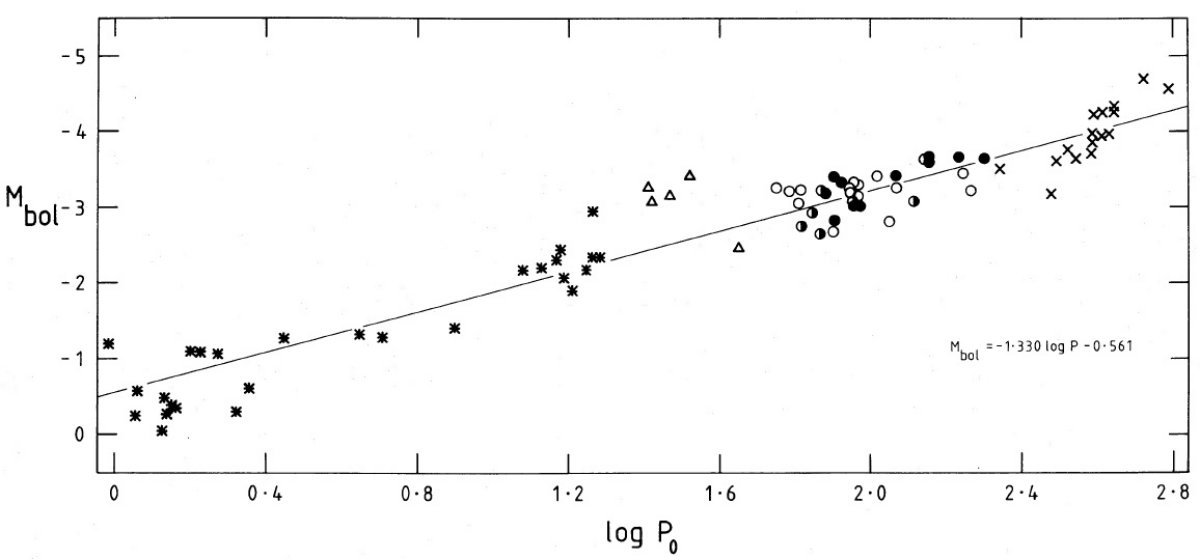
|
基本振動と第1倍音 図3に戻ると、実線=基本振動と第1倍音に対する P - Te 関係式で、式3 で第1倍音を P/2 と考え、式1中の Q と M には前に使用した値を入れた。 低メタル星と基本振動、高メタル星と第1倍音の間の相関は大変良い。低メタル 星が基本振動ラインより上にあることは、それらの星の質量が 0.65 Mo 以下 (理論的に予想されている値)であることを示唆しているが、不定性が大きい。 NGC 6121 と NGC 6712 NGC 6121 と NGC 6712 は基本振動と第1倍音変光星の双方を含むように見 える。Frogel et al 1983 は色等級図上の巨星枝の位置を使って、「赤外メタル 量指数」を導いた。これは Zinn 1980 のメタル量と良い一致を示す。 | ただ、いくつかの星団には差が見られる。NGC 6121 では、[Fe/H] = -0.72 (Zinn, -1.46), NGC 6712 では、[Fe/H] = -0.92 (Zinn, -1.17) であった。これらの メタル量は星団を高メタル量グループに分ける。明るく高温の NGC 6121 V4 は基本振動、通常の巨星枝変光星 V13 は第1倍音と考えられる。NGC 6712 V7 はミラ型で第1倍音、V8 は基本振動、 V10 はどちらもあり得る。 Wallerstein, Cox 1984 はセファイド不安定帯の赤側の縁が Mbol = -2.5 付近 で殆ど水平になることに着目した。その結果、これより明るい赤い星は脈動する。 Te > 3700 K の星は基本振動し、それより低温の星は第1倍音で振動する。 メタル量が中間で、温度が 3700 K 付近にある星が二重モードを持つと考える ことも可能である。 |