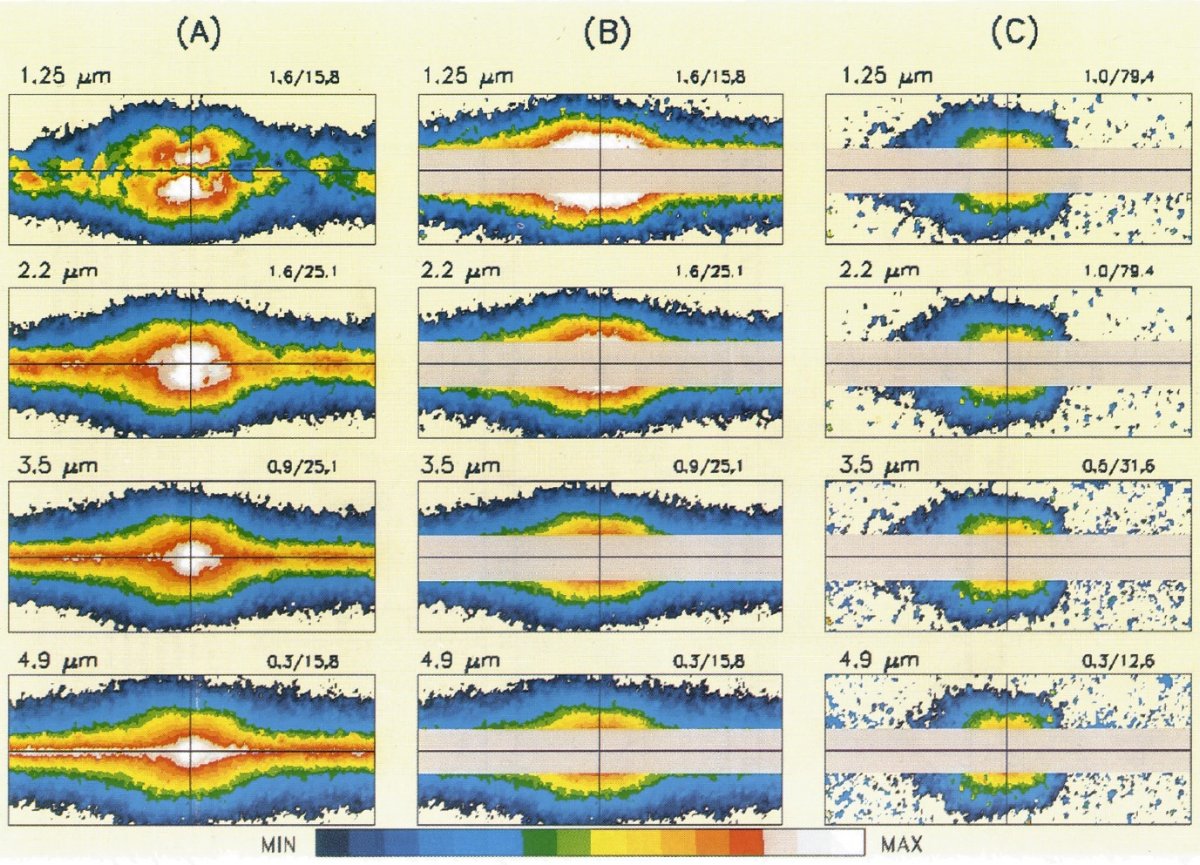
| COBE/DIRBE 1.25, 2.2, 3.5, 4.9 μm のバルジ低分解マップを示す。 減光補整および円盤成分除去の後、バルジの輝度分布は短軸対長軸の比が 0.6 の楕円形になった。 | バルジ短軸のスケール高は 4 波長全てで 2°.1±0°.1 であった。 バルジの輝度分布等高線の銀経非対称性は定性的には第1象限に先端がある 3軸不等バーから予想されるものと一致する。銀河面からの傾きの兆候はない。 |
1.イントロダクションBlitz, Spurgel 1991, Nakada et al 1991, Whitelock, Catchpole 1992, Weinberg 1992 はバルジが軸対称でないことを発見したが、データの不足から その形までは決められなかった。 COBE/DIRBE は 0.7° の分解能で全天を撮像した。その 1.25, 2.2, 3.5, 4.9 μm 画像はバルジの形を調べるのに最適である。 |
2.データ惑星間塵放射のフィッティング関数を差し引いた残りの精度が 1.25 - 3.5 μm で 1 - 2 %, 4.9 μm で 5 % である。図1a はそれらのマップを 示す。バルジは NIR でははっきり見えるが 12 μm では判然としない。 1.25 μm ではダストによる減光の帯が銀河面に沿って走っている。 |

3.1.減光補正DIRBE は他波長画像を提供するので、短波長側画像に見えるデコボコが実際 の構造か、減光の効果かを長波長画像から判断できる。 Arendt et al. 1994 は DIRBE 1.25/2.2 μm カラーに基づいて減光の τ(1.25) マップを作成した。2.2, 3.5, 4.9 μm の減光光学的深さは Rieke, Lebofsky 1985 の減光則から決められた。この減光マップにより輝度分布の 減光補正を行った。この手法はバルジ全体が減光スクリーンの向こう側にある という仮定に依存している。 |b| < 3° ではこの仮定が怪しい。 そこでこの区域は解析から外した。もう一つ、減光強度は 1.25/2.2 カラー から決めたので、この2バンドの減光補正マップは独立ではない。3.2.バルジの形ピーナッツバルジHauser et al 1990, Hauser 1993 による DIRBE 1.25, 2.2, 3.5 μm 合成画像は Blitz, Spergel 1991, Rich 1992, Whielock 1992, Binney et al 1991 によりピーナツ型バルジの証拠とされた。 Combes et al 1990, Sellwood 1993 の N-体計算シミュレーションによるとバーバルジはピーナッツ または箱型に見えると予想されていた。図1a, 1b から明らかにバルジは扁平で ある。しかし、減光補正の前と後とではバルジの形状に変化がある。特に、 1.25, 2.2 μm 減光未補正画像の (l, b) = (1, 4) に見られる等輝度線の 窪みが強調されるのは減光の効果である。この構造はバーナード 78 複合 (Lynds 1962) に対応する。この複合は小さく濃い暗黒雲の集まりで、可視 写真で容易に見分けられる。この領域はバルジの |b| < 3 外側では最も 減光が強い。赤化補正された画像ではこのピーナッツ的窪みは弱くなっている。 円盤成分 赤化補正画像 1b はバルジと円盤の重ね合わせである。円盤成分は I(l, b)disk=I(0,b)diskexp[-|l|/lo(b)] とモデル化する。DIRBE データ |l| ≤ 90, 3 ≤ |b| ≤ 10 を用いて 円盤成分を表現する。l = 10 - 30 のリング成分によるコンタミを防ぐため、 I(l, b) の下包線を使用してフィットする。lo(b=0) は外挿から求められたが 30 - 40 であった。(ただし |b| = 0 - 3 は使わない。) モデル円盤成分を除いたバルジ画像を図 1c に示す。その特徴は、 (1)見かけの形 4バンドでバルジの形は同じ。見かけ短軸/長軸比は 0.6 である。 (2)バルジスケール高 bo |b| ≤ 10 での短軸沿い強度プロファイルはドボークルー則よりは A exp[-b/bo] でよくフィットされる。これは Kent et al 1991 が既に注意 していた。彼らが 2.4 μm データから出した bo = 2.7 は DIRBE 2.2 μm 減光未補正データの結果とよく一致する。減光補正したデータでは DIRBE 4 バンド, |b| = 3 - 10 で bo = 2.5 が得られた。円盤の差っ引き後のデータでは b = 2.1±0.2 となった。Blanco 1988 は M 型巨星から bo = 2.0 を得た。 |
(3)銀経非対称性 l = 0 ラインに関し等輝度線は非対称である。l = 12 - 15 ではバルジの尾が 銀河面に伸びているように見える。これはバルジ固有の性質ではなく、 l = 10 - 30 に付加構造があるためかも知れない。今回の単純モデルではこれは 扱わない。この構造は Kent et al 1991 や Ruelas-Mayorga 1991 により 渦状腕、リングなどとされてきた。しかし、この「尾」を無視しても第1象限 でのバルジの大きさは第4象限よりも l で 2° 大きい。 (4) |l| ≤ 7 では、第1象限での bo(l) は第4象限での bo より大きい。 図2にはその比較を示した。円盤成分は引いていない。 (5)箱型バルジ バルジ等輝度線はピーナッツ型より箱型に近い。しかし、中間輝度での 等輝度線には l = 0 付近で弱い窪みが見える。ただしこれは円盤差し引きの モデルに依存する。 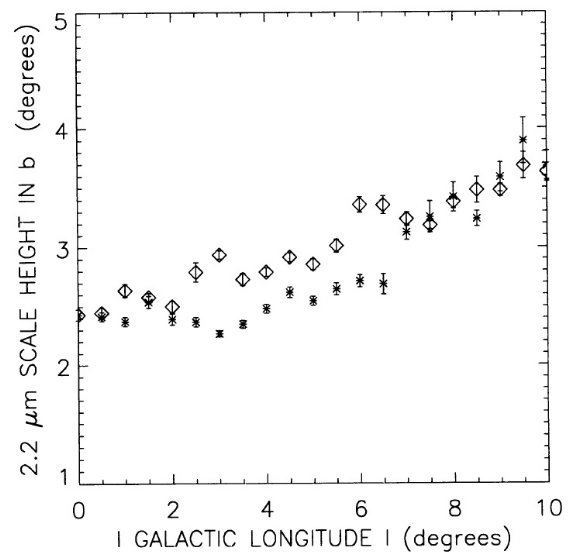 図2.2.2 μm でのバルジスケール高 bo の銀経変化。アステリスク= 第4象限。菱形=第1象限。 |
|
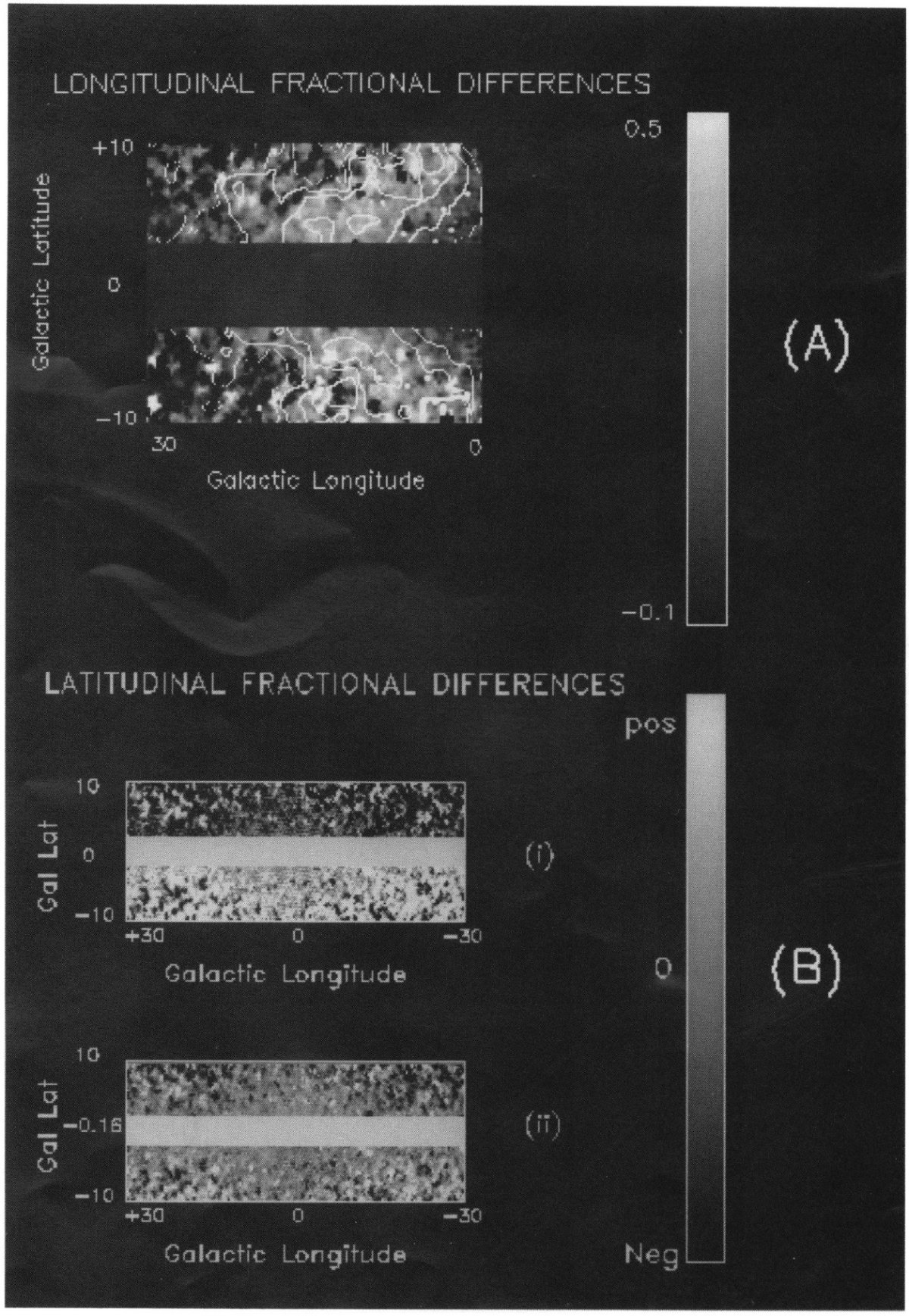
輝度相対差 α = バーの銀河面上での傾き、α=0 は先端がこっち向き、 α=90 は完全に横向き。β = 銀河面に対するチルトとする。 Blitz, Spergel 1991 に従い、輝度相対差を定義する。 l = 0 に対し: ΔIl=[I(l,b)-I(-l,b)]/I(l,b) b = 0 に対し: ΔIb=[I(l,b)-I(l,-b)]/I(l,b) Blitz, Spergel 1991 の α=45, β=0 モデルの計算結果に基づき、 以下の予想が立てられる。 |
1.バー先端が第1象限にある時、ΔIl は正で l と共に増加する。 2.l=0, b=0 付近で、ΔIl のサインが交替する。 3.第1象限のスケール高は第4象限より大きい 図3aには、減光補正画像の ΔIl を示す。l = 15 まで系統的な 増加を示す。l = 15 より先ではこの傾向はなくなる。また ΔIl に b = 0 非対称は見られないのでチルトは検出されない。 ΔIb には構造が認められない。ただし、 b= -0.16 での 折り返しが著しく差を減少させる。おそらく太陽位置が高いせいであろう。 0.16 は 8.5 kpc では 24 pc に相当する。 |
| COBE/DIRBE 観測の 1.25, 2.2, 3.5, 4.9 μm データを減光補正して、 さらに円盤成分を差っ引いた。その結果、バルジの形はピーナッツ型よりは 箱型に近いことが分かった。 | バルジ等輝度線の非対称性は Blitz,Spergel 1991 のモデルの予想と定性的に 一致した。チルトを導入する必要はない。 |