Distances of the Galactic Supernova Remnants by Red Clump Stars


Shan, Zhu, Tian, Zhang, Wu, Yang
2018 ApJS ,



　アブストラクト　

　銀河系第１象限の SNRs 距離を測定した。レッドクランプ星を標準光源と減光 探索子に用いて、個々の　SNR 方向で Av - D 関係を導出した。１５個の SNRs 距離が導かれた。 　G65.8-0.5, G66.0-0.0, G67.6+0.9 の距離は初めて得られた。また、32 天体の 距離上限・下限を与えた。G5.7-0.1, G15.1-1.6, G28.8+1.5, G78.2+2.1 の距離 は以前より改善された。今回求まった距離の殆どは以前の距離推定値と矛盾しない。

　１．イントロダクション　

　減光と距離の探索子としてのレッドクランプ　

　 Girardi (2016), Gao et al. 2009 はレッドクランプ星を減光の研究に用いた。 Lopez-Korredoira et al. (2002) は視線に沿った星の分布を調べた。 		　X 線源の距離　

　Durant, van Kerkwijk 2006 は X 線パル サー方向で距離・減光関係を調べ、パルサー距離を求めた。Guver et al 2010 は X 線連星の距離を、Zhu et al 2015 は SNR G332.5-5.6 への距離を与えた。

　２．Av - D 関係　


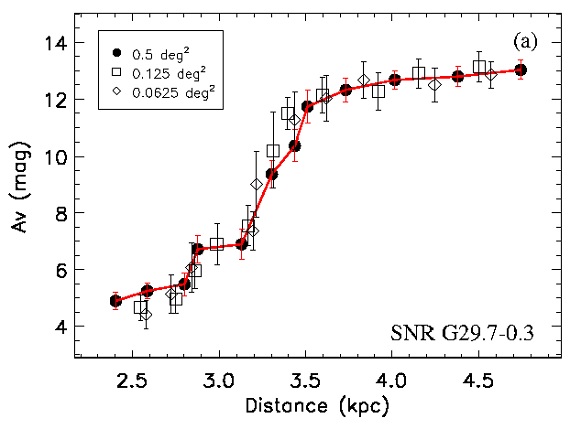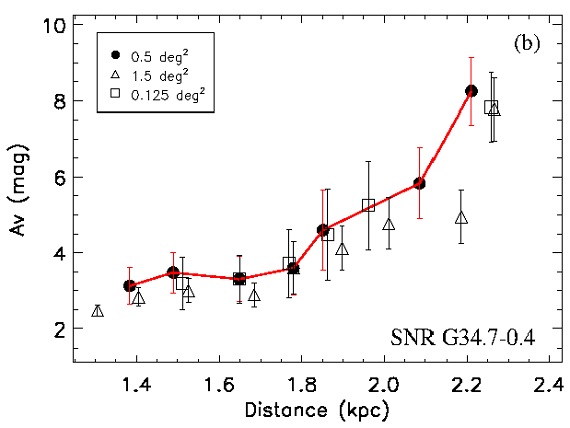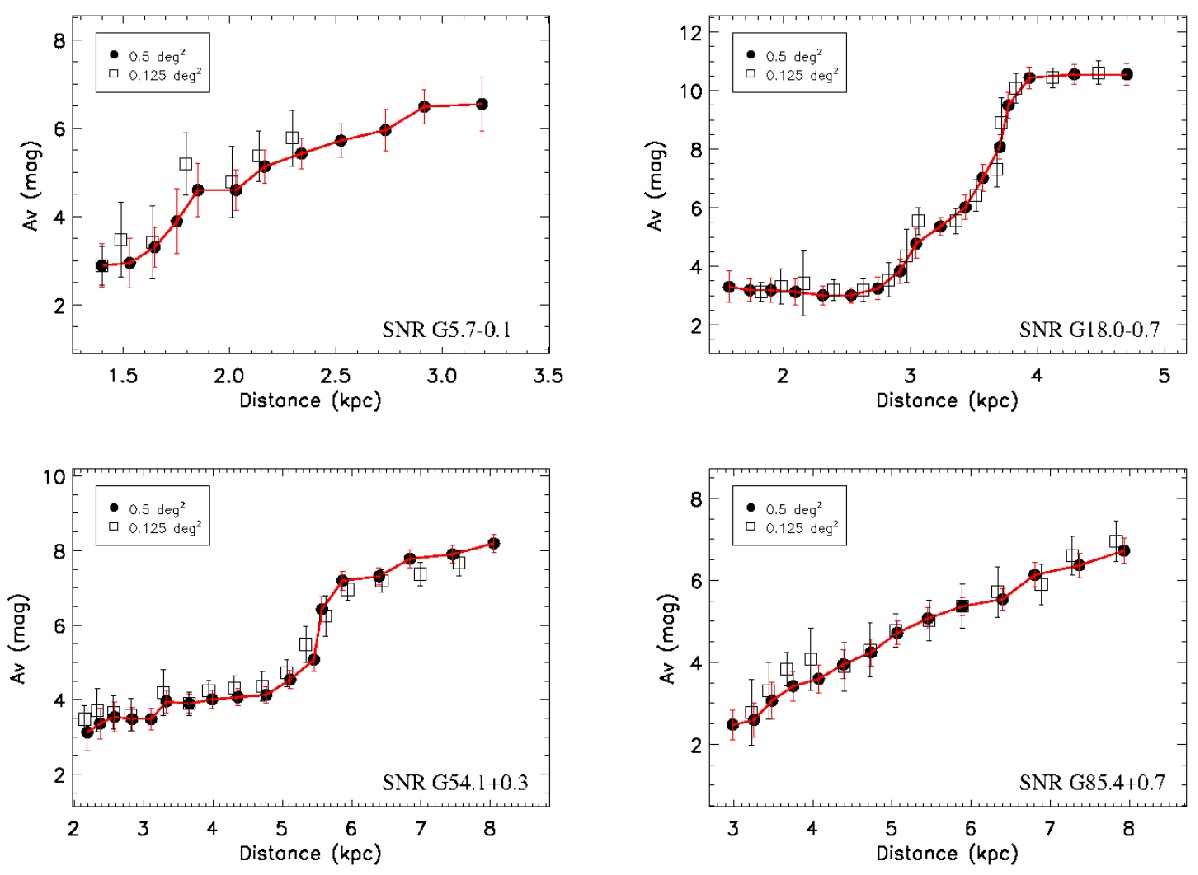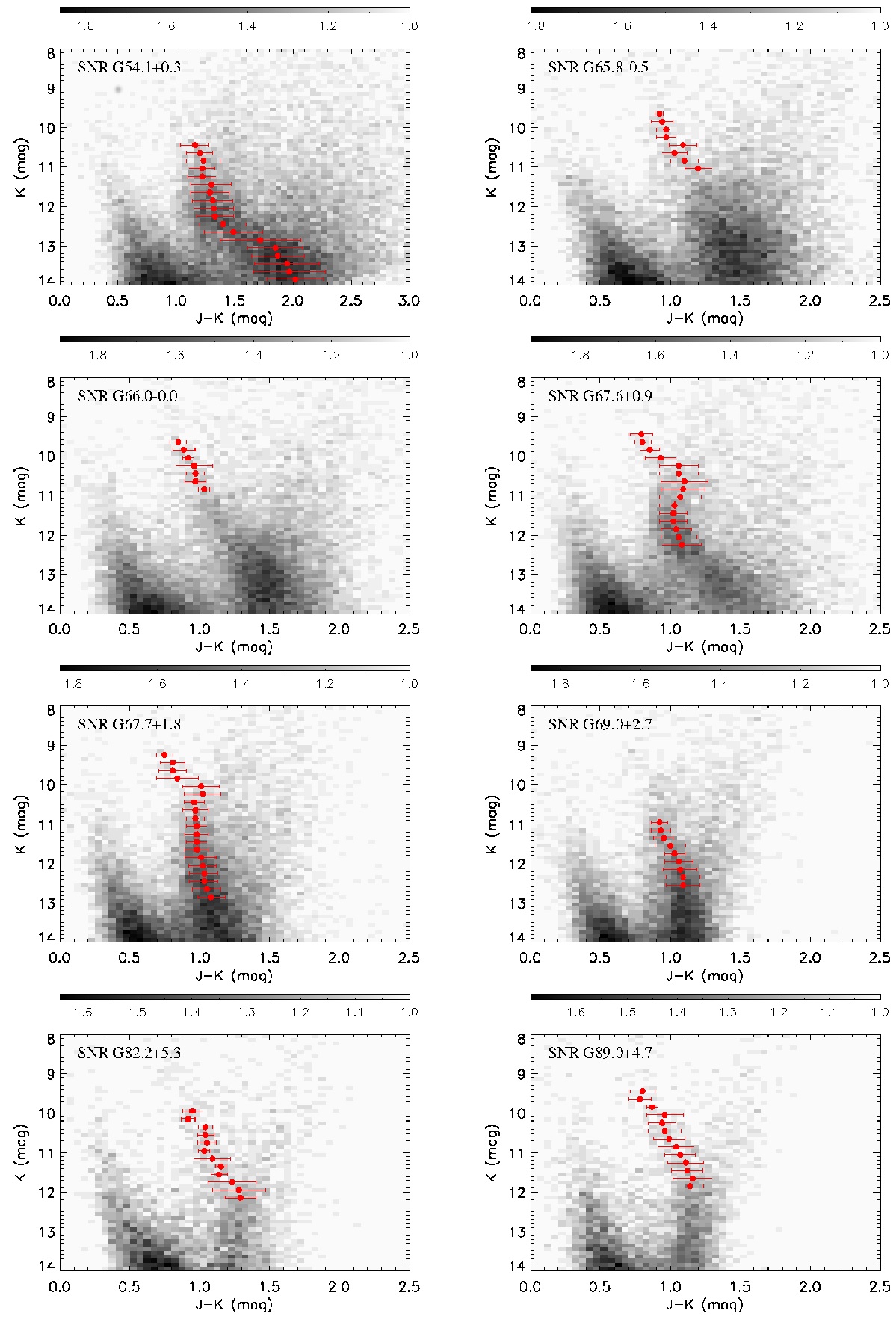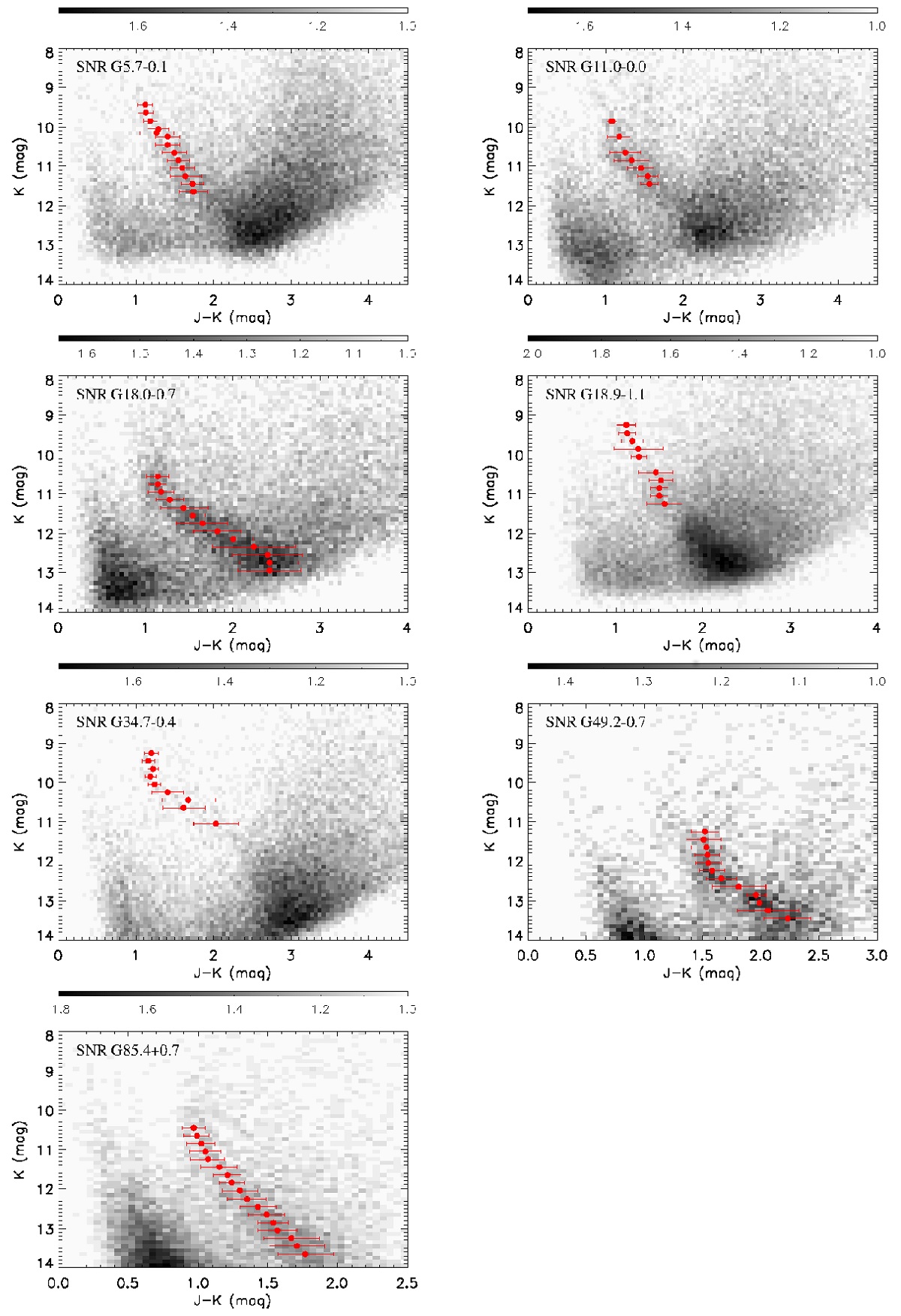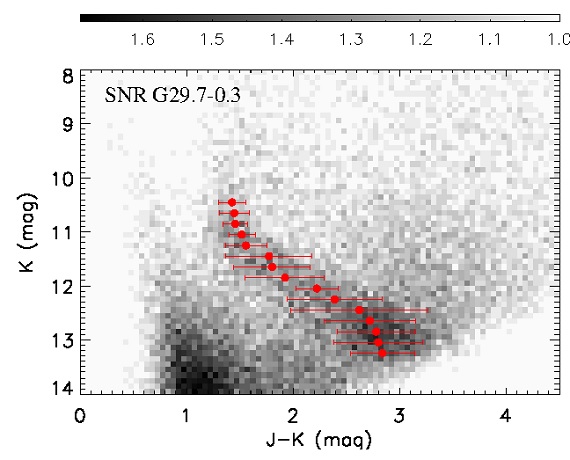
図１．G29.3-0.3 まわり 0.5 deg2 内 21032 星の CMD. グレース ケールは星密度を対数表示している。赤点＝ RC 密度ピーク。赤横線＝ 1σ.

　図１：G29.7-0.3 方向の例　

　我々の手法を提示するため、 G29.7-0.3 を例に説明する。図１に天体を中心 に ΔlxΔb = 1°x0.5° の 2MASS CMD を示す。図の左側に 主系列星、中央に RC 星、右に矮星と赤色巨星が並ぶ。RC 星を K 等級で 0.3 等幅の水平な帯に分割する。RC 星密度が低い等級では、この幅は 0.5 - 0.7 等に広がる。帯の横幅は、 RC 星の大部分を含み、かつ他種族星の混入が最小 となるように決める。帯毎の星分布を次の式 (Duran, van Kerkwijk 2006) で フィットする。
y=ARCexp { -[(J-K)-(J-K)peak]2 } +AC(J-K)α
2σ2


ここに、ARC = RC 星の規格化、AC = 混入星の規格化 を表す。

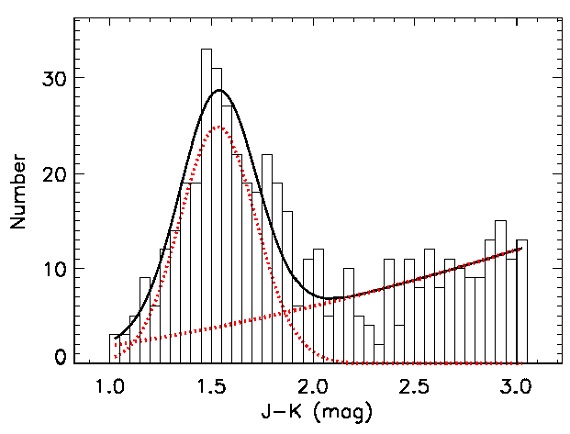
図２．K = [11.1, 11.4] における (J-K) ヒストグラム。黒線＝ベストフィット。 点線＝ガウシアンとべき乗則成分。

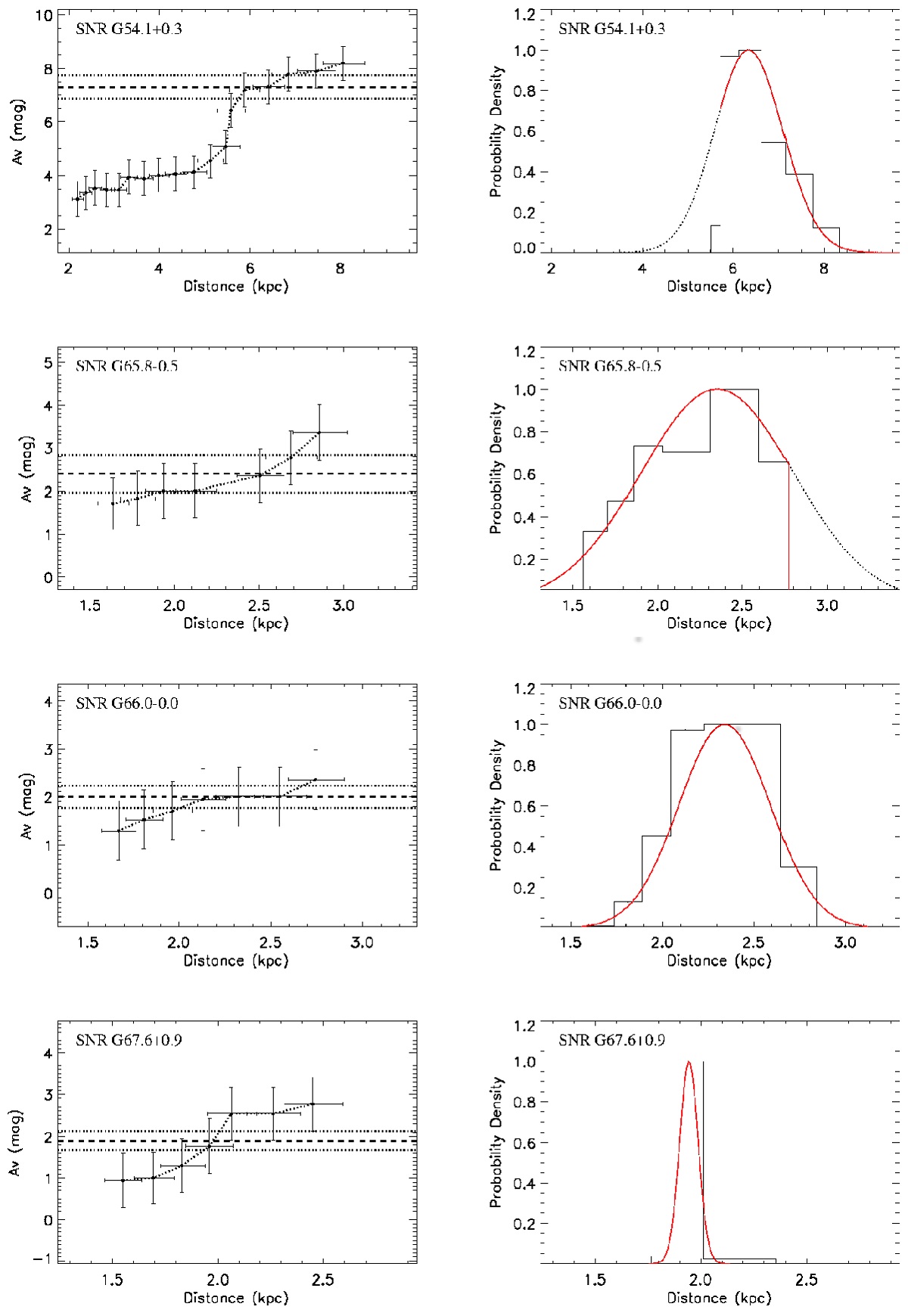
　図２＝帯中心の減光と距離　

　図２には K = [11.1, 11.4] 帯でのカラー分布と、それへのフィットを示す。 この例では、(J-K)peak = 1.56, σ = 0.19 である。 RC の平均固有カラーと絶対等級を (J-K)o = 0.63, Ko = -1.63 と仮定すると、 帯中心の減光と距離が以下の式から分かる。

　　　AK = 0.67 [(J-K)peak - (J-K)o]

AK = 0.1615 - 0.1483
AV RV


　　　D(kpc) = 10[0.2(mK-MK+5-0.1137AV]/1000

　Rv = 3.1 を採用した。また、 AK と Rv の関係は Cardelli et al. (1989) による。


図３a．赤線＝ G 29.7-0.3 を中心とする 0.5 deg2 の Av-D 関係。 黒線＝ 0.0625 deg2 の Av-D 関係。

　測定範囲の実験　

　この解析を 2MASS 測光限界まで続ける。最良のサンプル領域はどのくらいだろうか？ 大きければサンプル数が増える。小さければ領域内の減光の不均一性が減少する。 図３a では、星の表面密度が高い領域でのテスト結果を示す。 0.5 deg2=1°x0.5°, 0.125 deg2=0.5° x0.25°, 0.0625 deg2=0.25°x0.25° の３種類の範囲で 試した。図から分かるように３通りの結果は互いにほぼ一致する。 1.5 deg2=1.5°x1°, 0.5 deg2=1° x0.5°, 0.125 deg2=0.5°x0.25° の３種類の範囲で 試した。図を見ると、 0.5 deg2 と 0.125 deg2 の 結果はほぼ一致するが、1.5 deg2 の結果は系統的に低めに出る。 領域を広げると、減光の散らばりが大きくなることの反映である。そしてそれ はカラー分布の巾に現れる。

図３b．赤線＝ G 34.7-0.4 を中心とする 0.5 deg2 の Av-D 関係。 黒線＝ 0.0625 deg2 の Av-D 関係。

　最適サイズは 0.5 deg2　

　従って、減光の分散＝カラー分散が変わらない限りはなるべく大きな領域の サンプルを選ぶことにした。通常は 0.5 deg2 が良いバランスを 与えることが分かった。

　SRC = 第２ RC 星は効かない　

　最近、RC に主要部と第２構造 SRC があることが分かってきた。主要部は 低質量で縮退ヘリウム核を持つ。一方、SRC 星のヘリウム核は非縮退である。 Wan et al 2015, 2017 は LAMOST DR3 から RC : SRC = 3 : 1 とした。 SRC の効果を調べるため、二重ガウシアン関数でフィットを試みたが明瞭な 第２成分は検出できなかった。したがって、我々の方法では SRC 効果は無視する。


　図４．サンプル領域を変化させたときの Av-D 関係。赤線＝ 0.5 deg2　


　３．Av, NH と D の比較　

　Green 2014, Ferrand, Safi-Harb 2012 のカタログから、我々は第１象限の 161 SNRs を選び出した。その内 47 SNRs に対しては文献から可視減光 Av または水素コラム密度 NH が見つかった。それらを我々の方法と 比較した結果を表１と表２にまとめた。

　３．１．可視減光　Av　

　ライン比　

　よく使用されるライン比は Hα/Hβ で ある。その他、[SII]10320A/[SII]4068A と [FeII]1.6435μm/[FeII]4068A も使われる。共通の上準位からのライン同士の比はガス温度や密度の影響が 小さいので、減光を測るのに適している。

　付随星の減光　

　もう一つの方法は、SNR に付随し、距離が既知の個々星の減光を測定する ことである。

　３．２．水素コラム密度 NH　

　Zhu et al. 2017 は 銀河面第１，４象限で、NH/Av = (2.04±0.05) 1021 H cm-2 mag-1 を得た。NH は 0.25 keV 以上の重元素吸収と相関がよいので、 X 線が検出される約半数の SNR では　NH　がしたがって Av が 評価可能である。

　３．３．距離 D　

　距離評価法には、運動学距離、固有運動、減光、Sedov　法、付随天体距離 など様々である。我々は、運動学距離、固有運動、付随天体距離、Sedov　法、 Σ-D 関係の優先度で文献から距離を集めた。


表１．可視減光 Av - D 関係


表２．水素コラム密度 NH-D 関係

　図５．減光量がRC 測光範囲にあった 15 SNRs 方向の CMD. 　



　図６．左： RCs の Av-D 関係。破線＝ SNR の Av. 点線＝ Av 不確定性。 右：SNRs 距離の確率分布。　





　４．不確定性　

　５．結果と議論　

　第１象限 47 SNRs 中 32 SNRs の減光は RCs 減光の範囲外であったので、 減光の上限または下限のみしか与えられない。残り 15 SNRs に対する CMD と RC 尾根を図５に与える。その方向の Av-D 関係と SNR 距離の確率関数を 図６に示す。

　５．１．SNR 距離　

　　

　P(D) = SNR 距離の確率分布、は Guver,Ozel,Cabrera-Lavers,Wroblewski (2010) に従い、 PSNR(Av) = SNR 減光の確率 分布、と PRC(Av|D) = PRC(D|Av) = 与えられた距離 区間内での RC 減光の分布。どちらの分布もガウシアンを仮定する。
(これまでの解析を読むと、ある K 区間内の RC 星は同じ距離にあって、様々な減光を受けている。さらに個々の RC 星の絶対等級、固有カラーは一つに固定されている。本当はこの二つは 両立しないんだけど。でも参考になった。)


　天体距離の決定　

　図６の右枠は上の式で計算した X-線源距離の確率分布を示す。この分布を ガウシアンで近似して、最尤値として天体距離を決定する。

　５．２．結果のまとめ　

　こうして 15 天体の距離を得た。 3/15 G65.8-0.5, G66.0+0.0, G67.6+0.9 は新しい距離である。それらは 2.4, 2.3, 2.0 kpc であった。 　その他に 20 天体には距離の下限、 12 天体には上限を与えた。

　５．３．議論　



　距離精度　

　15 SMRs の距離を求めた。図７ではその距離を他の手法で決めた距離と比較 した。大部分は他の手法で決めた距離と矛盾しない。




図７．(a): RC 距離と運動学距離との相関。(b): RC 距離と他の方法で得た 距離との比較。赤矢印＝下限。青矢印＝上限。

　６．まとめ　

　結構よく距離が決まった。