The Dictance, Mass, and Radius of the Neutron Star in 4U 1608-52

　アブストラクト　

　３．レッドクランプ法　

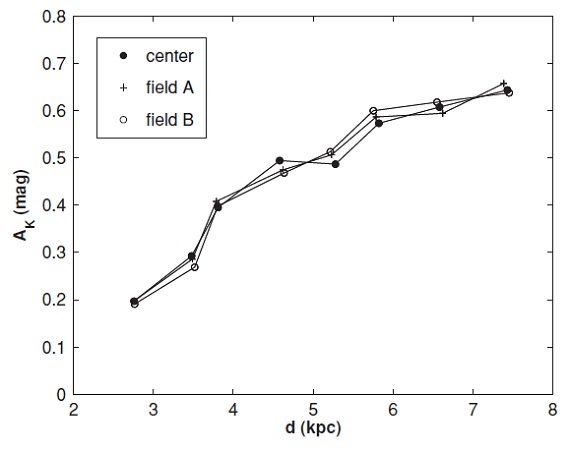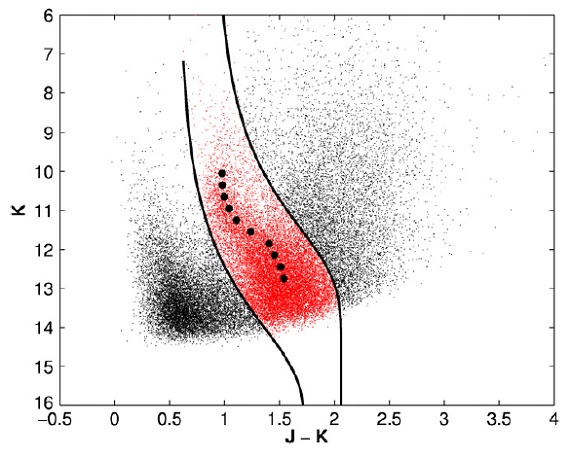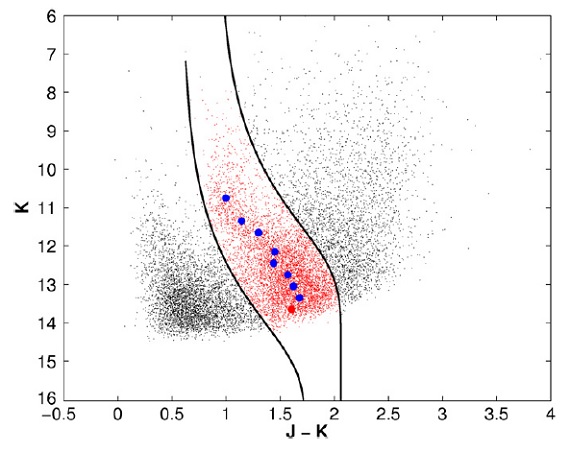
図２．4U 1608-52 (l, b) = (330.9, -0.9) 方向 0.15 deg2 の 2MASS CMD. 実線＝RC 領域。黒丸＝ 各等級区間での RC の密度ピーク。 　RC の固有カラー　 　MKs = -1.62±0.03, (J-Ks) = 0.7 を仮定する。 MKs は安定しているが、MJ はメタル量と年齢の 影響を受ける。その結果、 (J-K)o も両方に影響される。 Gonzalez-Fernandez et al. 2008 によると、 4U 1608-52 の方向 (l, b) = (331.0, -0.9) では 内側銀河系 RC のメタル量 [Fe/H] = -0.2 が予想される。その結果、この方向では (J-Ks)o = 0.67±0.01 となるであろう。

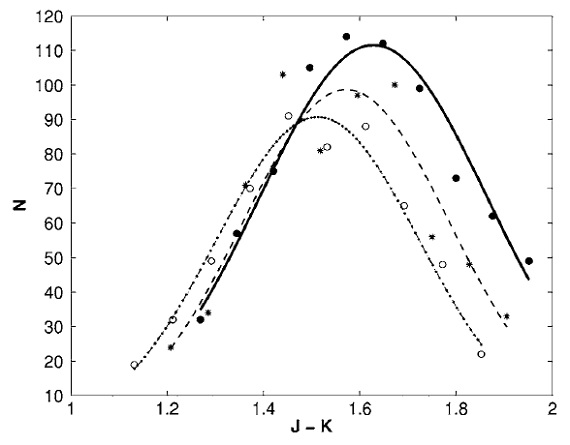
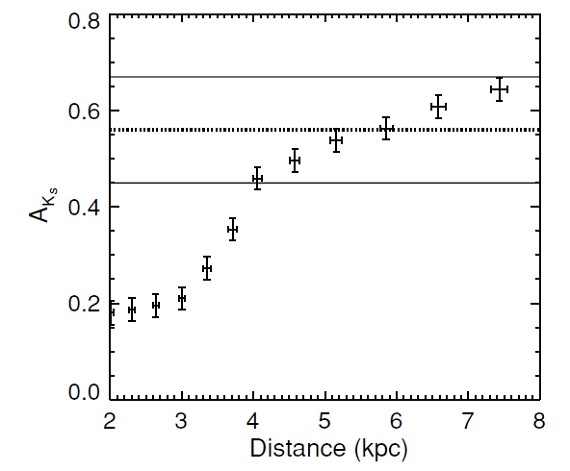
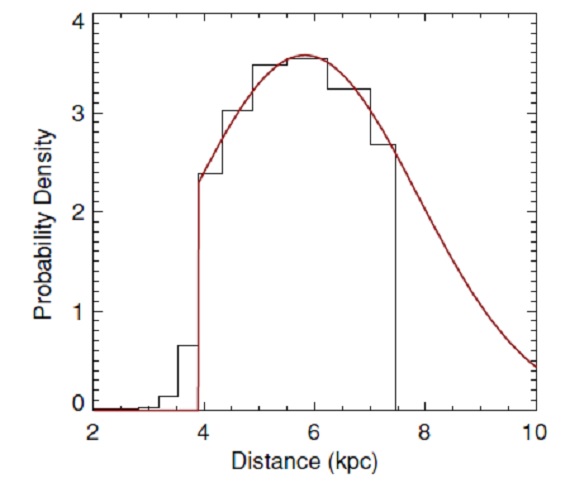
図３．RC カラー分布へのガウシアンフィット。実線は K = [12.6, 12.9]. 破線　K = [12.3, 12.6]. 一点破線 K = [12.0, 12.3] 　３．1. 4U 1806-52 への応用　 　図２は 2MASS CMD である。 UKIDSS はもう少し深いが、この天体方向は 観測データがない。 　図３は３本の Ks 帯に対する (J-Ks) 分布とそれらへのガウシャン フィットを示す。フィットの結果は帯の平均 mK 毎に 極大カラー (J-K)mK を与える。 Rieke, Lebofsky (1985), Cardelli et al. (1989) から、 　　　AK = 0.657[(J-K)mK-(J-K)o] すると、天体距離 D(pc) は、 　　　D = 10^[mK-MK+5-0.2AK]

図４．AK - D 関係。黒丸＝４U 1608-52 方向。 プラス印と白丸は l で 0.5° 離れた隣接領域。相互に大きな 差はない。 　３．２．4U 1698-52 の距離　 　隣接領域との比較　 　Δl = 0.5°, Δb = 0.3° サンプル 13,202 星を 使い、 D = 7.5 kpc までの減光を測ることができる。測定精度を 上げるにはサンプル領域を広げる必要がある。しかし、その際に領域内の減光 変化が小さいことが保証されなければならない。図４では対象領域とその 左右隣接領域での AK-D 関係を示す。図は大きな変化が無い ことを示す。 　図５＝拡大領域の CMD　 　そこで、Δl = 1.5°, Δb = 0.3° 40,584 星を 用いた CMD を図５に示す。

図５．図２と同じだが、面積を 0.45 deg2 と３倍にした。 　P(D) = X-線源の距離確率分布　 　Px(AK) = X-線源の減光確率分布 　PRC(AK|D) = PRC(D|AK) = ある距離区間ないの RC 星が減光 AK である確率 (PRC はつまり AK-D 面におけるレッドクランプ星の分布と思えばいいのか？ ) すると、X-線源の距離確率分布は、以下の式で与えられる。 　　　P(D) = ∫Px(AK)PRC(D|AK)dAK 図７には、こうして計算したP(D) を示す。AK は D = 3.9 kpc で明白な急落を示すので、図にはカットを入れた。こうして求めたベスト フィット距離は 5.8 kpc であった。

図６．4U 1608-52 方向 0.45 deg2 領域の 減光曲線。点線＝ 4U 1608-52 とその 1 σ 誤差。

図７．4U 1608-53 の距離確率分布とそのガウシアンフィット。カットは 3.9 kpc. ベストフィット距離＝ 5.8 kpc.