Constraints on the Evolution of Peculiar Red Giants II. Masses and Space Densities


Scalo, Miller
1979 ApJ 233, 596 - 610



　アブストラクト　

　様々な進化段階にある赤色巨星の理論的空間密度と初期質量分布を特異赤色 巨星 Ba, R, S, N(P giants) のに関する観測データと比較した。理論モデルは 半観測的な IMF と文献にある主系列星寿命、半観測的なマスロス率を合わせて 得た。星質量の観測データは変光タイプ、空間密度、運動学、連星、星団から 得た。Ba 星の空間密度はダブルシェルモデルで説明するには多すぎ、ヘリウム シェルフラッシュと何の関係もないことを示す。より冷たい P 型巨星の空間 密度は良く分からないが、ダブルシェル期の星の予期数は超えないだろう。 連星系と星団のＰ巨星データは 1 - 10 Mo と大きな広がりを示す。運動学から P 型巨星の平均質量は 1 - 1.5 Mo 辺りである。 　光度、空間密度、質量からの拘束を合わせると、（１） R-星の性質はヘリウム コアフラッシュ期のミクシングと合う、（２）Ba 星の大部分はヘリウムコア フラッシュと考えられる。ただ、ξ Cap, HD 65662 のような星は別のメカニズム が必要である。（３）ヘリウムコアフラッシュだけでは N, S 星のミクシングは 説明できない。（４）ヘリウムシェルフラッシュはぎりぎり低温 P 巨星の観測 制約をクリアする。（５）もし、ヘリウムシェルフラッシュが低温Ｐ巨星の 原因であるなら、観測される平均質量はコアマスが ≤ 0.7 Mo と小さい時に 起こるという制約を課すが、これは恒星進化計算では実現されない。

　１．イントロダクション　

　２．理論　

　寿命　

　各進化段階の寿命 Ti のパラメタ―を次式で近似する：
　　　log Ti = A0 + A1logM + A(logM) 2　　
表１に Ao 等を示す。

　光度　

　コア質量・光度関係は Paczynski 1970 より、

　　　L = K1(MC-K2)

である。太陽単位系で、K1=5.9 104, K2 =0.522 である。コア質量の増加率は、

　　　dMC/dt = 6.2 107(L/EHX) Mo/yr

上の二つを積分すると、

　　　L = L0 exp(t/τ)　　　　　(7)

τ = 1.3 106 yr, L0 = 中心でヘリウムが枯渇した 時の光度で、総質量に依存する。また、コア質量が Mc(t1) から Mc(t2) まで増加するのにかかる時間 Δt12 は、
Δt12 = τ ln [ Mc(t2) - K2 ]
Mc(t1) - K2
　マスロス　

　Reimers の式
　　　dM/dt = α(L/Lo)(R/Ro)/(M/Mo) Mo/yr　　と、
　　　L/Lo = (R/Ro)2(Te/To)4　　から、

　　　dM/dt = α1L3/2M-1T e-2　　　(10)

ここに、α1 = 2.94 107α である。ちなみに Reimers は α = -4 10-13 (= αR) を推した。

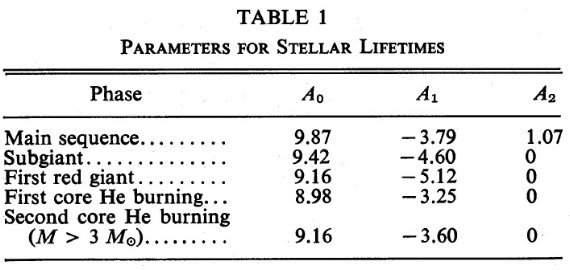
表１．各進化段階の寿命のパラメタ―

　AGB 進化経路　

　Ulrich, Scalo 1976 の AGB 進化経路を近似すると、
　　　Te = KTMbL-c(X/0.75)-d (Z/0.02)-e 　(11)
ここに、KT＝7.8 103, b=0.194, c=0.133, d=0.2, e=0.05 である。式７、１０、１１を使い、M, L, Te の時間変化が得られる。

　Sanner のマスロス　

　レイマースのマスロス式には疑いの声もあった。 Sanner (1975), Sanner (1976) は次の表式を与えた。

　　　log[-(dM/dt)] = S1 + S2Mbol (12)

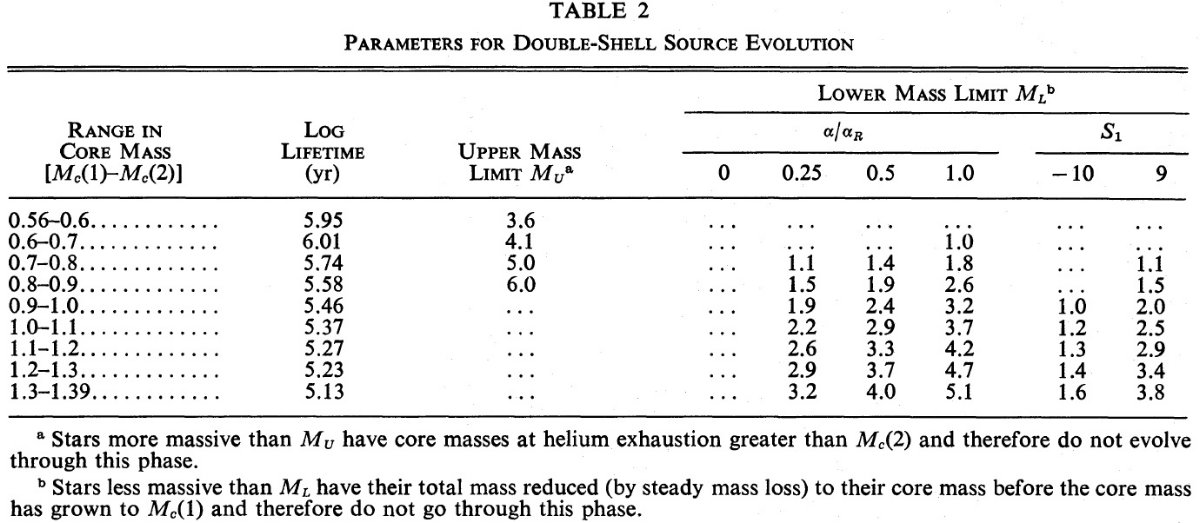
Sanner は S1 = -9.9±0.3, S2 = -0.51± 0.05 とした。ただし、共通する星について、他のマスロスの評価と較べると、 上式の絶対値は一桁程度の不定性を持つ。そこで、 S1 をフリー パラメタ―として扱い、レイマースの式と同じようにマスロスが終了する最低 質量を S1 = 10, -9 について示す。




表２．ダブルシェル燃焼星の進化パラメタ―
(最終列の "9" は "-9" のタイプミス？ )

　３．特異 P-巨星の相対数　



図１．コアマスが Mc 以上の星の空間密度。異なる星形成史と、マスロス率の 組み合わせに対して計算した。MD, MI とついているのは、形成史が減少または 増加する場合で、かつ初期質量関数の不連続が起きない最大値。ファクター α はレイマースのマスロス式の係数。

　空間密度から面密度へ　

　モデルは面密度だが、観測は空間密度である。そこで、空間密度から Blaauw 1965 が赤色巨星に与えたスケール高 300 pc を使って面密度を計算する。 雑だが、観測誤差が一桁程度あるので構わない。観測から得られた gK, gM, gC 星の総計は (2 - 6) 10-4 pc-3 であり、表３の (7 - 30) 10-4 pc-3 はそれより大分大きい。この 矛盾はおそらく 1 Mo 付近の星のコアヘリウム燃焼期寿命の推定値が原因であ ろう。この値は 1.5 Mo の星の値からの外挿を用いた。表３の最後の２行は 信頼できる。
( 赤色巨星全体の中で AGB 星が　 0.1 % ってちょっとあり得ないんじゃないか？何か誤解？ )


　Ba 星　略　

表３．予想される空間密度 (stars pc-3)
(最下行が図１の Mc = 0.6 Mo の所の 数値になる。 )

　炭素星の空間密度　

　P (特異) 巨星の空間密度は Westerlund (1965) しかない。彼は、 (低温Ｃ星)/(gM5-gM10) = 1/25 を 3/4 距離区分で見出し、 1/4 距離区分で 1/3 とした。Mavridis 1967, 1971, Nandy, Smriglio 1971a,b, 1976, The, Staller, Muers 1974 から、(gG-gK):(gM0-gM4):(gM5-gM6.5):(gM7-gM10) = 7000:100:5:(1-3) である。注意すると、 gM 星ないの相対比は銀河系内の 位置による。というのは、例えば、 M5-M10 星の分布は M2-M4 星より滑らか であるからである。M5-M10 星の空間密度は 4 10-7 pc-3 である。 Westerlund (1965) を合わせると、彼が調べた領域で N 星は (2-10) 10-8 pc-3 である。同様の結論を Blanco (1965) も太陽近傍で導いている。一方、深い赤外サーベイ Mavridis (1971) はその比として、 25, GCVS では 25 である。これらは Westerlund (1965) が gM5-gM10 を使って求めた比の値と良く合うが、gM5-gM10 の星は全 gM 星の 5 % しか占めていない。M 型巨星の空間密度は 6 10-6 pc-3 であるから、N-型星の空間密度は (2-6) 10-7 pc-3 となり、前段落で述べたの見積もりをはるかに上回る。この違いの原因の一つは データ選択効果にある。深い、赤外サーベイは晩期型星に重みがかかるので、 上に述べた比は晩期 M 型星に対するものと看做すべきかも知れない。そう考えれば、 Westerlund (1965) の値との一致も納得できる。もう一つ考慮すべきは最近 Blanco,Blanco, McCarthy 1978 （もっと良いのは Blanco,McCarthy,Blanco (1980) ） が最近発見した、C/M が SMC で 55 に達するという事実である。いずれにせよ、 N-型星の空間密度は図１からどんな結論を導くにも観測が不足している。 　N 型星の空間密度が良い精度で決まれば、図１は N-型星がダブルシェル燃焼 期の星から生まれるかどうかについてよいテストを提供するだろう。

　４．Ｐ巨星の質量　

　連星　

　連星中の炭素星は Olsen, Richer 1975 にまとめられている。 W CMa の伴星は B2V で、この連星は視線速度から OB アソシエイションに 属すると思われる。そのターンオフスペクトル型は B0 である。 すると炭素星母星質量は 10 Mo を越す。このように、炭素星質量が大きいと 考えられる炭素星は、他に UV Aur (> 4 Mo), TU Tau (A2III, > 3 Mo), BD-26°2983 (A5V, ≥2.2 Mo), SZ Sgr(A7V, ≥ 2.0 Mo) がある。 この他の候補連星では伴星の推定質量は 1.1 - 2.2 Mo である。

　星団　

　星団の帰属に必要な視線速度の観測がないケースが多いので、やや問題 だが、表４に P 巨星のリストを示す。炭素星の同様な表は Barbaro, Dallaporta 1974 を見よ。もし、これらが全て本当に星団メンバーであったら、 P 巨星の 質量は 1 - 10 Mo に亘ることになる。NGC 457, NGC 7419, NGC 3114, NGC 6883 の炭素星については視線速度の決定が必要である。

　銀緯分布　

　Keenan 1954 と高柳 1960 は低振幅と非変光の S-型星は長周期変光 S-型星 より銀河面集中度が高いことを指摘した。Barbaro, Dallaporta 1974 は炭素星 を変光タイプ毎に銀緯分布を調べ、円盤への見かけ集中度が Mira-SR-Lb の順 に上がって行くことを示した。炭素星の大部分は SR と Lb だが、ミラ炭素星 が古い種族を作ることは、運動学的研究やこれから述べる話からも確認される。 未解決の問題は、 SR と Lb の間にどんな違いがあるかという点である。 後で述べる議論によると、 Peery 1975 に反し、Lb と SR に大きな質量の違い はないが、 Lb の方が幾分若いようだ。Yorka, Wing 1979 は非変光 S 星の銀 河面距離の平均値として、Mvis = -1.0 を仮定して、 ⟨Z⟩ = 200 pc を与えた。 		Catchpole, Feast 1971 は SC 星に似た値を与えた。 Dean 1973a,b, 1976 はミラ以外の炭素星に、⟨Z⟩ = 180 - 240 pc を与えた。彼等 はミラ炭素星では ⟨Z⟩ = 400 pc とした。以上の ⟨Z⟩ は 全て仮定した絶対等級に依存する点は注意が必要である。もし、以上の値が 正しければ、 S, SC, 非変光炭素星の質量は 1.2 - 1.4 Mo, 炭素星ミラは 1 Mo となる。

　銀経　

　低温炭素星の銀経分布は渦状腕に沿って見る方向で明らかなピークを示す。 このため、これらはしばしば渦状腕天体種族と看做された。S 型星についても 同様な結論が Keenan 1954 と高柳 1960 によって導かれたが、Yorka, Wing 1979 は否定的である。Westerlund 1964 も LMC 炭素星が LMC 円盤全面に亘る 構造と良く合うことを見出した。これ等の特徴は古い種族Ｉのものなのである。 見かけ構造を種族に結びつける危険は Cameron, Nassau 1955 M 型ミラを 渦状腕天体とした例からも明らかである。

　投影された銀河面分布　

　良く知られているように、銀河面上に投影した時に渦状構造を示す主系列星は B3 より早期の星である。Keena 1954 は SR とミラを除いた 31 S 星が渦状 構造を示すのではないかと述べた。高柳 1960 も同様の結果を出した。Peery 1975 は Lb 型炭素変光星 60 個の分布が渦状構造とゆるく相関しているとした。しかし、 詳しく、余計な天体を排除すると相関は見えなくなる。Ｐ巨星が渦状構造を なすという証拠はない。

　表面分布　

　詳しい解析をすると、 P 巨星の分布に関しては銀河面高度にやや違いが ある以外の情報は得られていない。

表４．星団と星群中の P 巨星。

　運動学的質量　

　Dean 1973a,b, 1976 は 427 炭素星の視線速度を解析した。様々なグループ 分けで解析した結果、二つのタイプが残った。C0 - C4 (多くが早期Ｒ型)と 炭素ミラは G-型矮星と似た運動学特性を有する。これは平均質量 1 Mo を意味 する。もう一つ、つまり残りの星は C5 - C6 型および C6 より晩期の SR と Lb 変光星で、F5 矮星と似る。この第２グループは Dean サンプルの 69 % を 占めるが、したがって平均質量 1.3 Mo で、若いおよび古い円盤種族の混合 である。速度分散は Lb が SR より若い証拠を示さないが、銀河面からの平均 高度はそのような効果を示唆する。いずれにせよ、 SR と Lb 炭素星の大部分 は F0 (1.6 Mo) より早期型の主系列星から進化している。

　Mira - Sr - Lb の順に若くなる　

　Mira - Sr - Lb の炭素星系列が次第に若くなっていくことは、 以上の銀緯分布と運動学からほぼ確立された。M-型巨星も同じ 系列に沿って銀河面への集中が強まる。同時に、銀河中心方向 への集中、平均銀河面高度、視線速度、速度分散は減少する。

表５．　変光タイプの割合。 　

　炭素星種族の二成分説について　

　Eggen 1970 は速度 (U, V) 図に低温炭素星をプロットした。その図は大部分 が古い円盤種族に属することを示した。これは我々の得た結論と合う。 その図には二つの星が全体から外れて位置することを示していた。かれは それらを HR 図上に載せて、質量＝ 9 Mo の若い種族星とし、炭素星が二つの 種族からなる二成分系であるとした。Crabtree, Richer, Westerlund 1976 も LMC 炭素星について同じ結論を出したが、２成分を裏付ける証拠はない。

　変光タイプ　

　前節では S, M 型星では Mira-SR-Lb と順に若くなっていく傾向があること を知った。Merrill 1960 の仕事依頼 GCVS は星数を 3 倍に増やした。
　表５を見ると、炭素星の変光タイプは S-, M-型星と異なる分布を示す。S-, M-型星では約半分がミラで、残りを SR と Lb で分け合っている。 N-星では Lb, SR が増えて、ミラが減っている。前節の話とつなげると、これは若い 種族の混入が S-, M-型星より大きいことを意味する。炭素星 SR の中では SRb = 周期変化や不安定な変光曲線、の割合が高い。ミラ型星同士を較べる と、 M-S-C の順で周期が長くなっていく。これは Merrill 1960 が既に述べて いることで、図２に示されている。その平均周期は 300, 360, 382 d である。 M-型ミラの場合、周期と種族タイプの相関が明らかになっている。それは、 平均密度が低くなるためかも知れない。それよりありそうなのは、S-, C-型星 が M-型星より少し若い種族に属していることである。良く知られているように、 運動学と空間分布から M-ミラは種族型と周期の間に相関がある。同様の比較 を SR の周期分布について行うことはここではしない。というのは、 これ等の星の周期を定めることは困難であり、かつ Feast, Woolley, Yilmaz 1972 が M-型 SR の周期と運動学の間に強い相関はないことを見出している からである。　

図２．M-, S-, C- 型ミラの周期分布