The Oosterhoff Period Groups and the Age of Globular Clusters II. Properties of RR Lyrae Stars in Six Clusters; The P-L-A Relation


Sandage
1981 ApJ 248, 161 - 176



　アブストラクト　

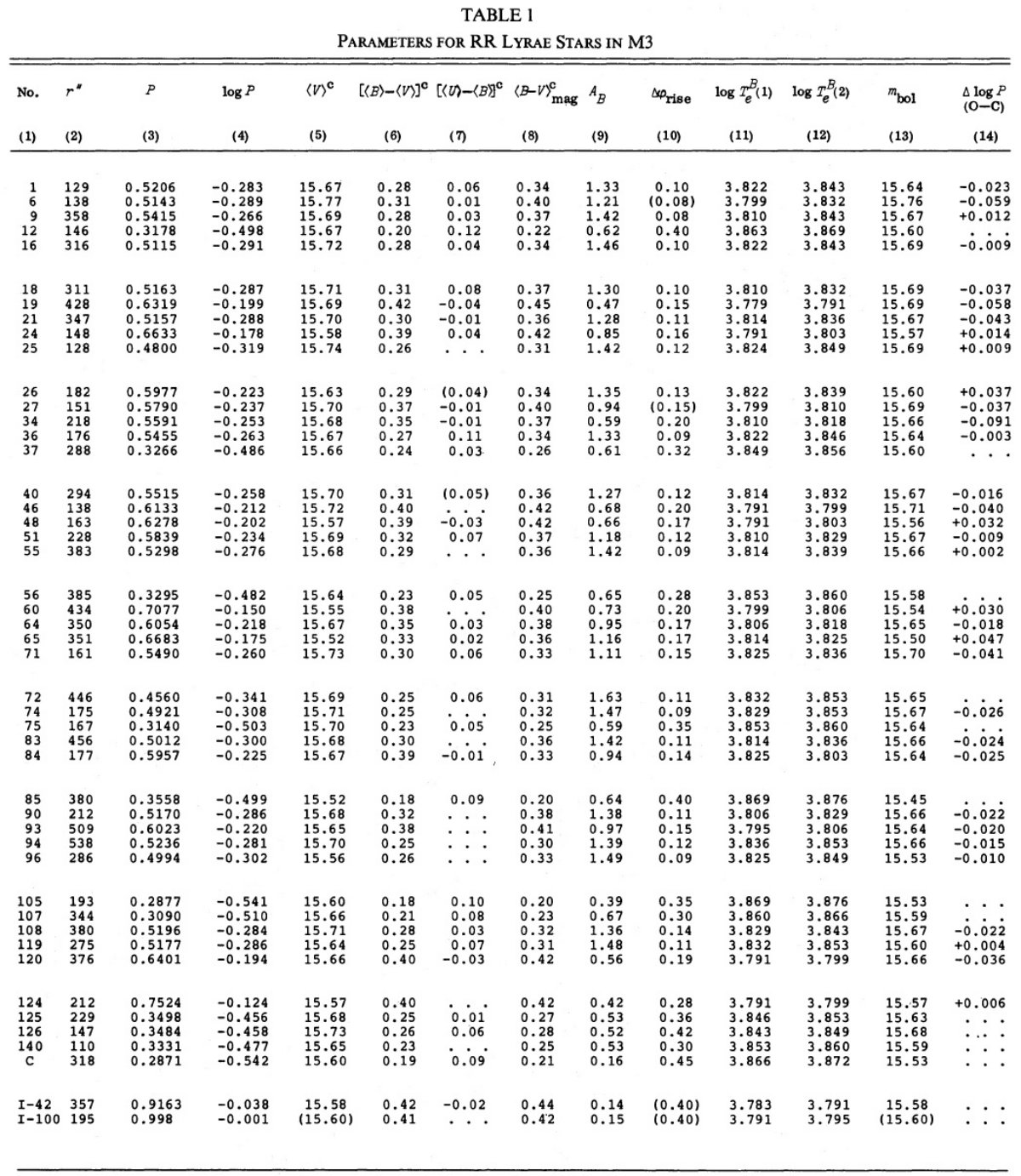
　6 球状星団の RR Lyr データを用いて、論文Ｉの結論＝異なる Oosterhoff グループ間の変光星同士ではどの温度でも周期シフトが存在する、をテストし た。 M3, M4, M5, M15, NGC6171, NGC6891, ωCen の変光星は周期・温度 関係が周期・振幅関係と同じシフトを示した。温度・振幅関係にはシフトがない。 　周期残差 Δlog P を M3 と ωCen の個々の変光星で決めると、 見かけ等級と相関があった。こうして、LRR の広がりは実際にある。 　同じ星団中で、Te と A を固定すると明るい変光星は長い周期を持つ。データ は ΔMbol = 3 ΔlogP, これは質量固定で、 P⟨ρ⟩ = 一定から予想される関係、と矛盾しない。 振幅固定で周期のズレを観測される等級変化と組合すと、周期・光度・振幅関係 が、Mbol = Mbol(M315.52) - 3(log P + 0.129 AB + 0.088) という形で求まる。Mbol(M315.52) は M3 RR Lyr 星 mbol = 15.52 の絶対等級。周期・振幅関係の係数 -3 は　モデルが予想するように、質 量がメタル量の関数なら、 -4.2 かもしれない。

　１．イントロダクション　

　２．データ　

　２．１．Ｍ３　RR Lyr のパラメタ―　




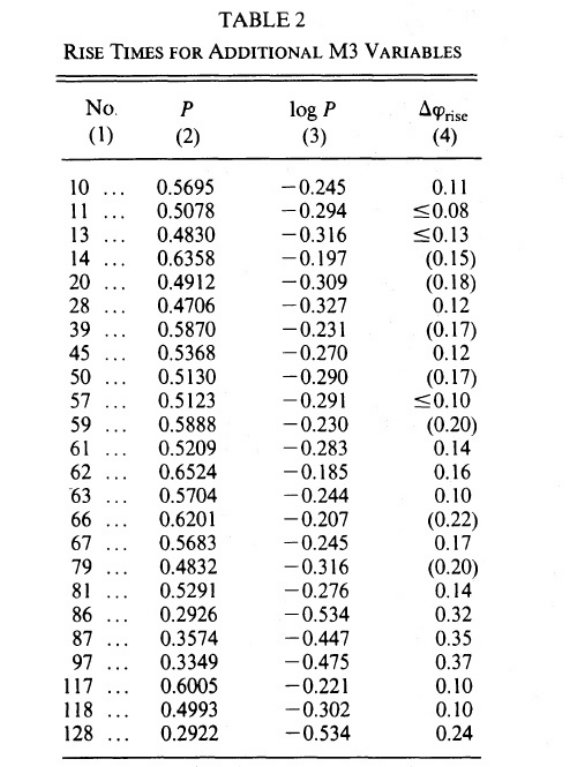表２．M3 変光星の増光時間 　

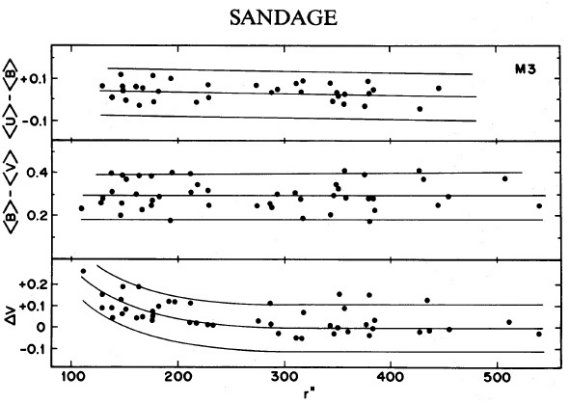図１．M3 星のコンタミ相関 　

　２．２．NGC 6121 RR Lyr のパラメタ―　




　２．３．NGC 6171 RR Lyr のパラメタ―　




　２．４．NGC 6981 RR Lyr のパラメタ―　




　２．５．ωCen RR Lyr のパラメタ―　




　３．周期、温度、振幅、増光時間の間の相関　


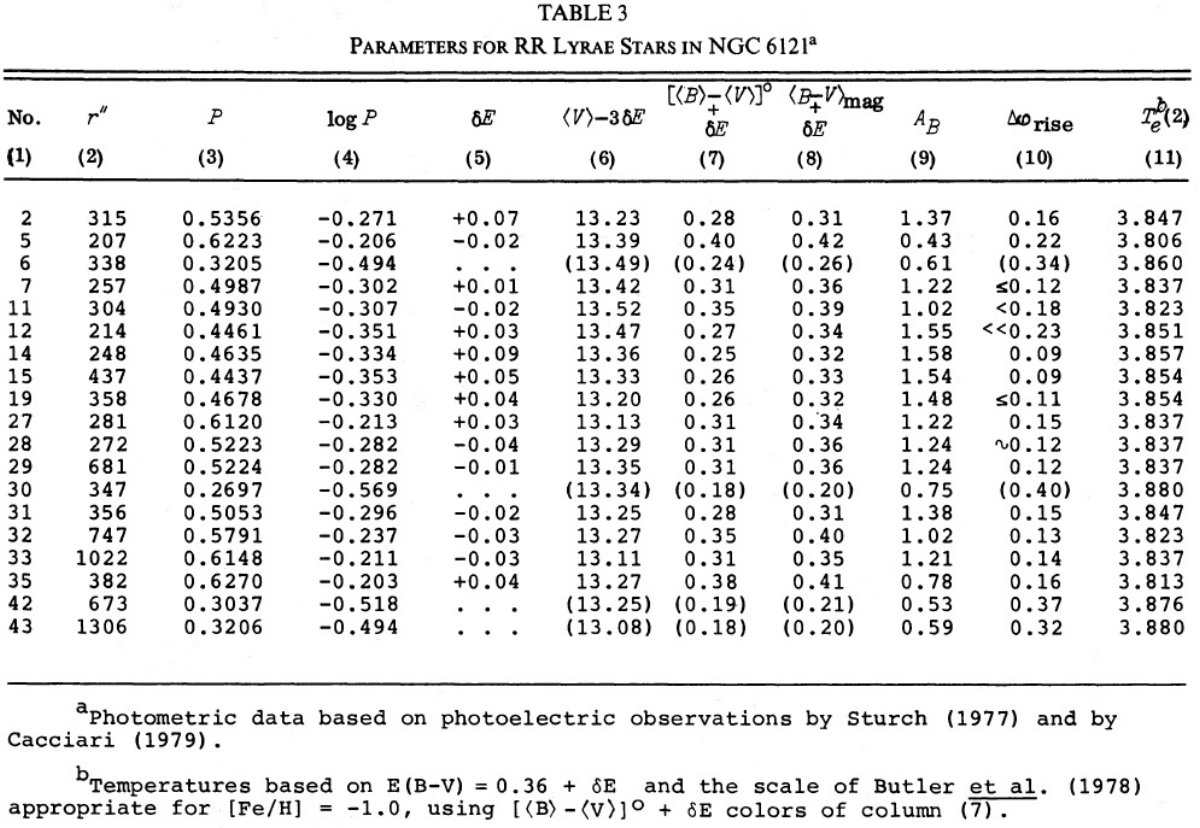
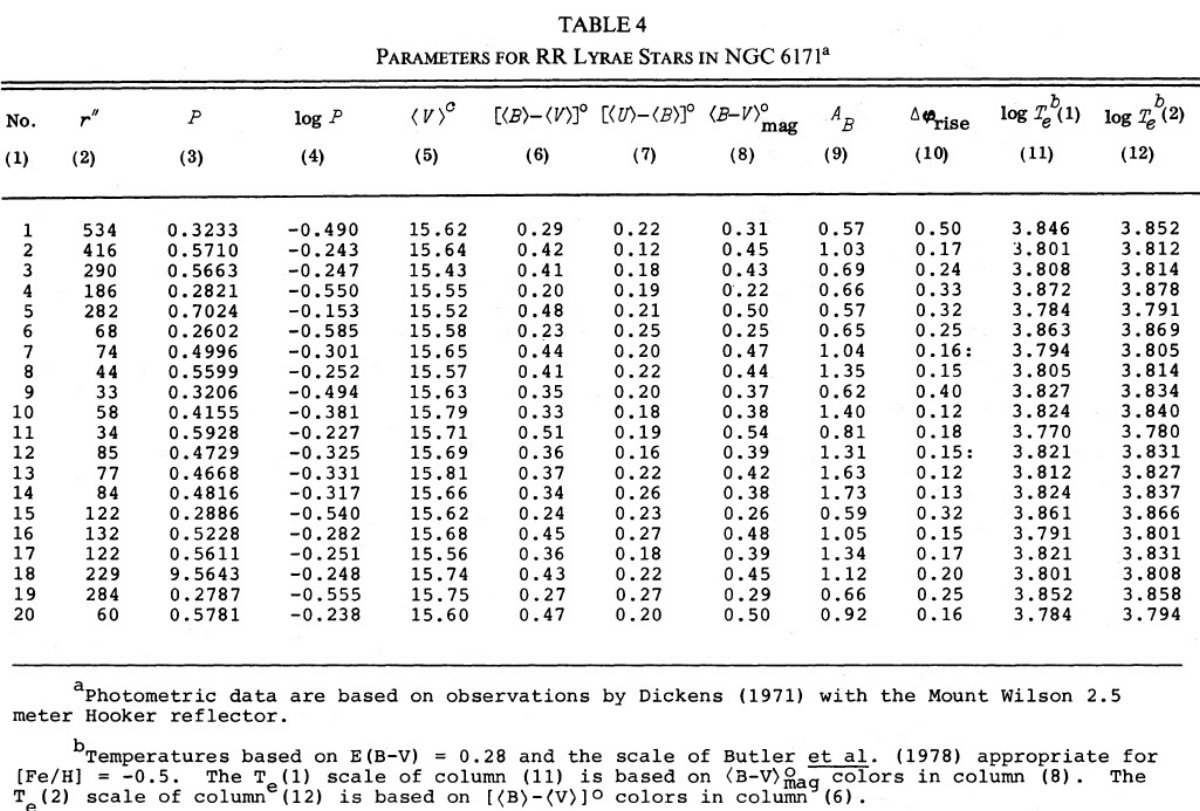
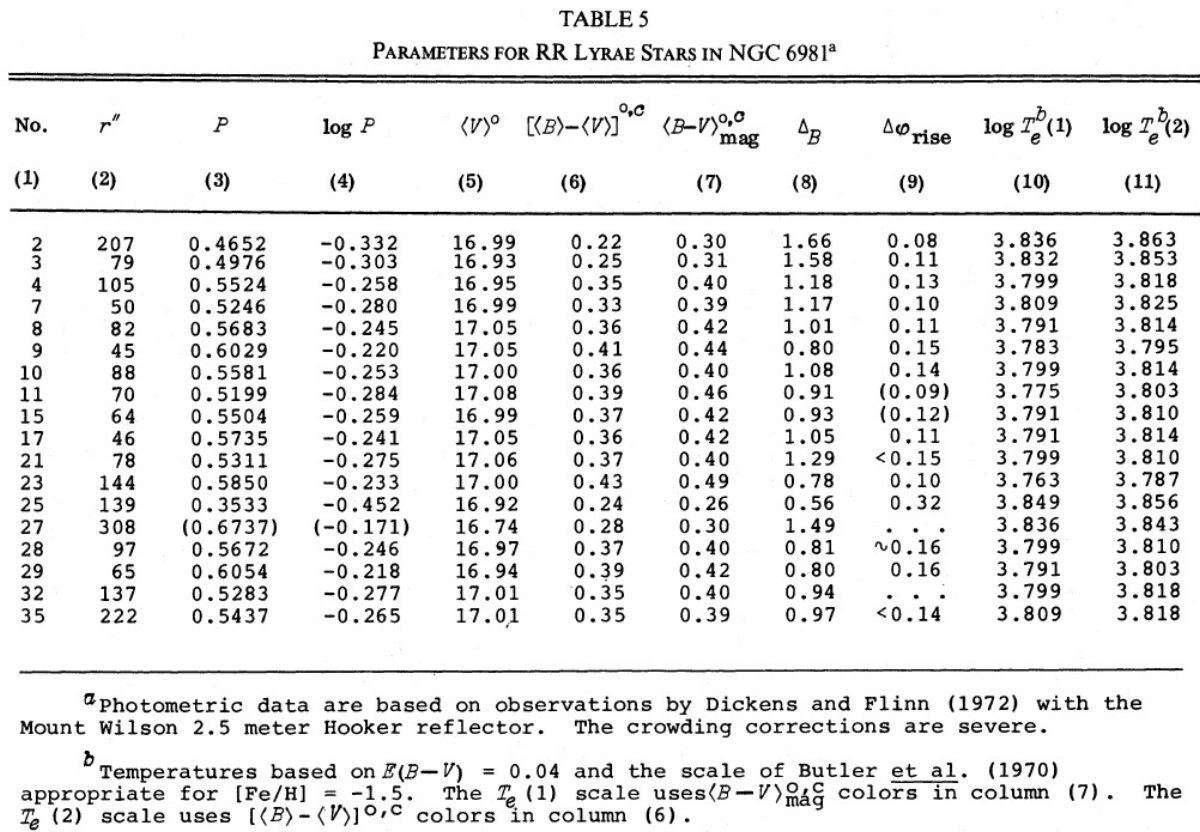
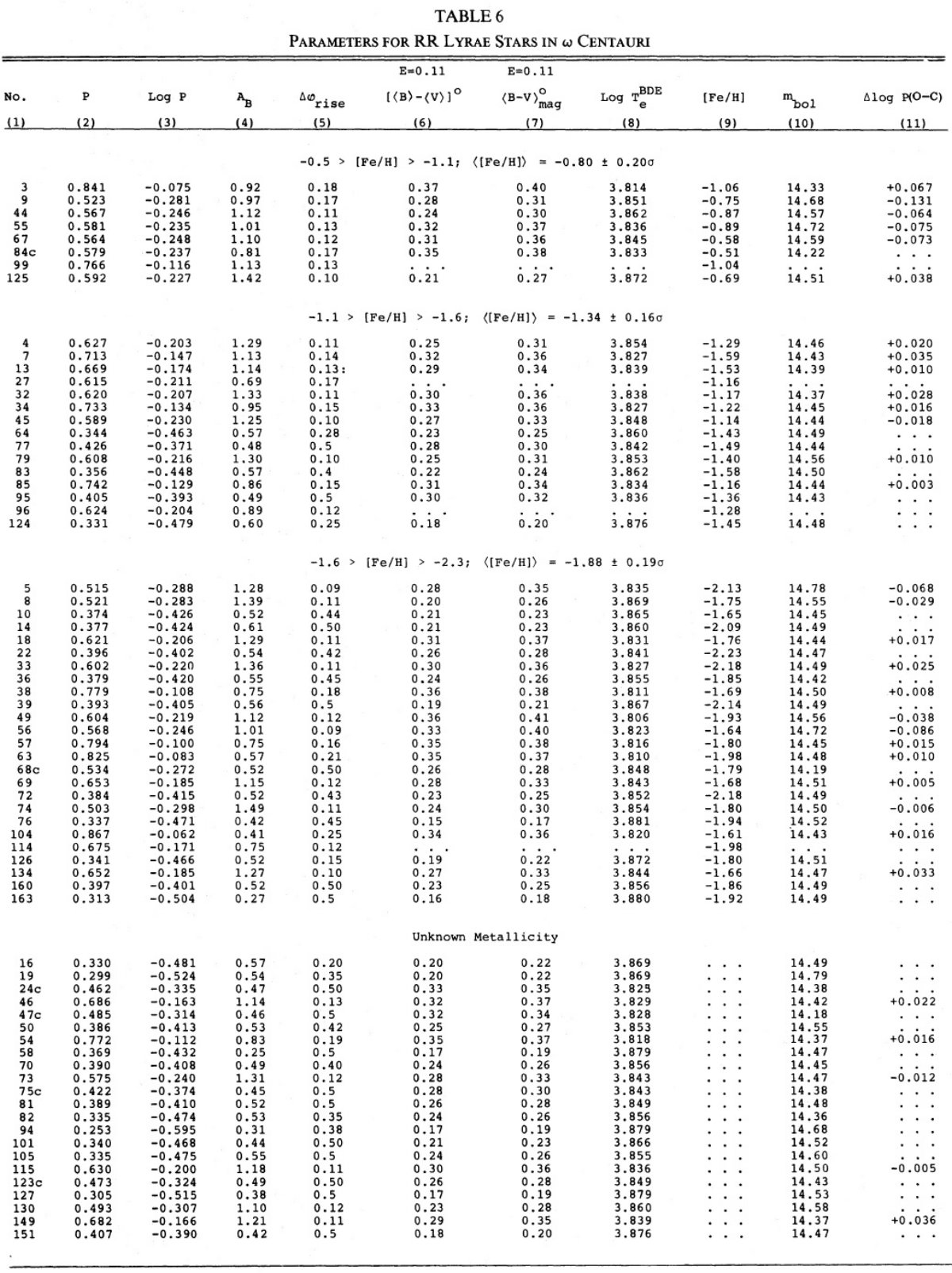
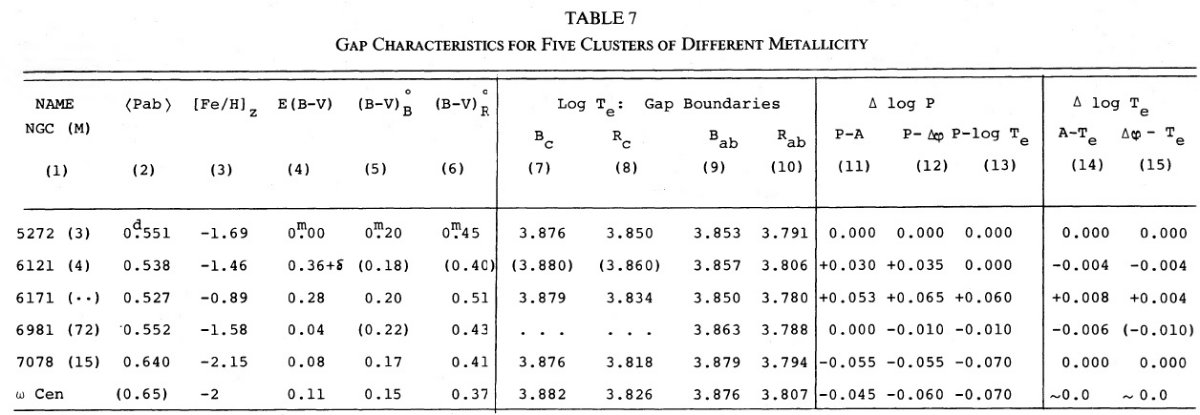
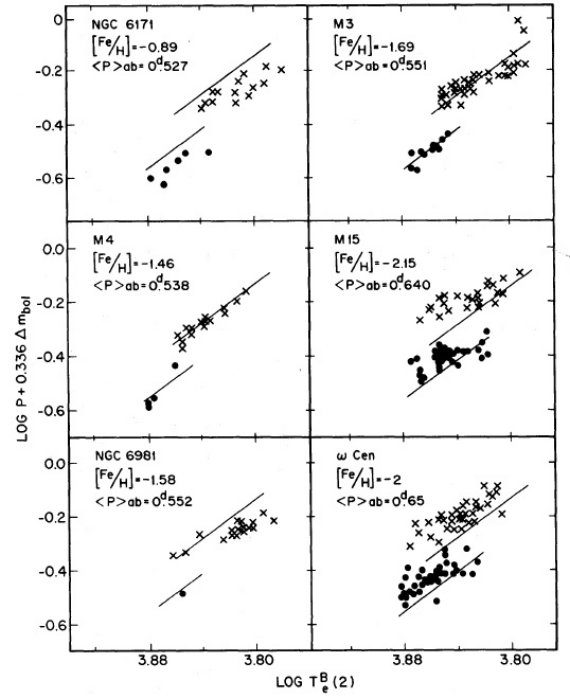図２．６星団の(reduced P)-温度関係。図はメタル量順に並べた。 reduced period = log P + 0.336 Δmbol. ここに、 Δmbol=mbol-⟨mbol⟩. 式（１）の左辺である。 　

　星団拡大　

　Oodterhoff 周期シフトはグループ II 変光星の絶対等級がグループ I よ り明るいためであるということからは、グループ II の周期・温度関係がグル ープ I と異なることが導かれる。与えられた温度で周期が異なるのである。 この論文ではこれらの関係を M3-M15 ペアから ６星団に拡大する。

　脈動条件　

　Ritter ぼ脈動条件 P⟨ρ⟩1/2 = Q は次の形に 書ける。

　log P + 0.336mbol = -0.68logM - 3.48logTe + const.　(1)

論文Ｉと同様、最初は質量項は落とそう。与えられた星団内の変光星が 不安定帯内での進化の結果光度が上がることによる固有分散を避けるために、 我々は logP+0.336Δmbol = reduced 周期 = 整約周期？　 を用いる。ここに、Δmbol = m - ⟨m⟩ である。

　図２＝整約周期・温度関係　

　図２で星団はメタル量の順に並べた。Te2 は ⟨B⟩-⟨V⟩ から導いた Te である。図中の実線は M3 に対する関係である。図から

（１）同じ星団の変光星は M3 に対し大体同じ ΔlogP だけずれる。

（２）NGC 6171, M 3, M4 ではタイプ c と ab とで Te が重ならないが、 M 15, NGC 6981, ω Cen では大幅に重なることである。

　図３＝周期・振幅関係　

　図３には同様のシフトを周期・振幅関係に示す。ここでも実線＝ M 3 ライン である。同様の周期シフトが認められる。表７にシフト量を示す。

　図４＝周期増光期比率関係　

　論文 I でも述べたが、周期シフトは変光曲線の増光期比率からも決まる。 そのデータを図４に示す。シフト量は表７に示す。

　表７＝諸量　

　表７には他の量も載せた。第２列にはタイプ ab の平均周期を、 Zinn 1980 からの [Fe/H] は第３列に、第４列の赤化は論文 III から採った。 第５，６列には不安定帯の青と赤の縁の赤化補正値を示す。対応温度は Te2 である。 　第１倍音＝タイプ c の青縁温度は、星団間の最大 ΔlogP = 0.12 = ω Cen - NGC 6171 間の差を説明するのに必要な δMbol = 0.4 mag の差にも拘わらず、すべての星団で共通である。 　表７の第１４列には振幅・温度関係シフト、第１５列には増光期比率・温度 関係シフトを示す。モデルによればそれらはゼロが期待される。実際、ゼロに 近い。

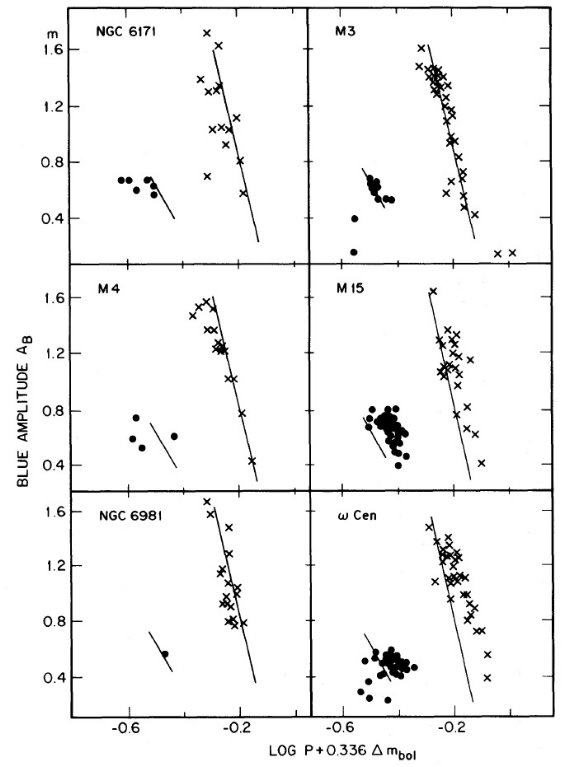図３．青振幅-reduced 周期関係。M3 にフィットしたラインを全ての図に描いた。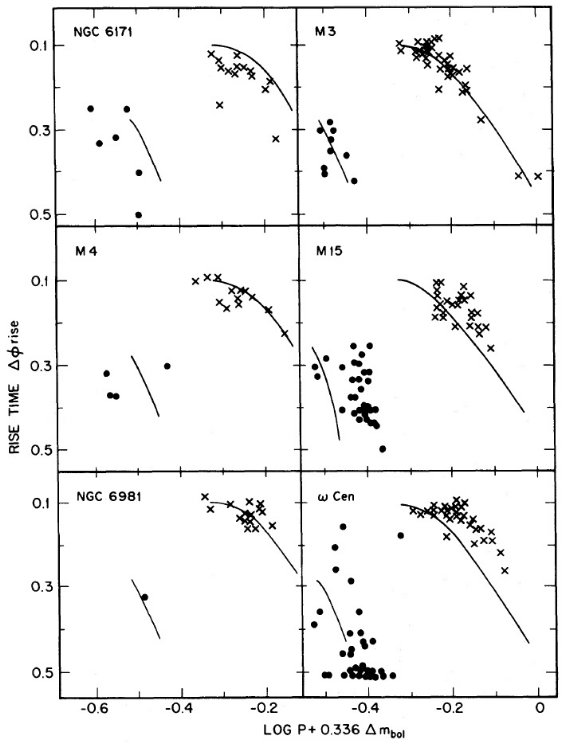 　


図４．reduced-周期-増光時間割合の関係。M3 の関係を書きこんだ。 　



　「Oosterhoff 問題は光度の差が原因」は正しい　

　これらの結果から、Oosterhoff 問題は光度の差が原因であるという 解釈は６星団の場合にも適用されることが分かった。




表７．メタル量の異なる５星団のギャップ特性

　　

　　

　

　　

　

　　

　 		　　

　

　　

　

　　

　



図．

　４．絶対等級の固有分散と RR Lyr の質量　


　　

　　

　

　　

　

　　

　 		　　

　

　　

　

　　

　



図．


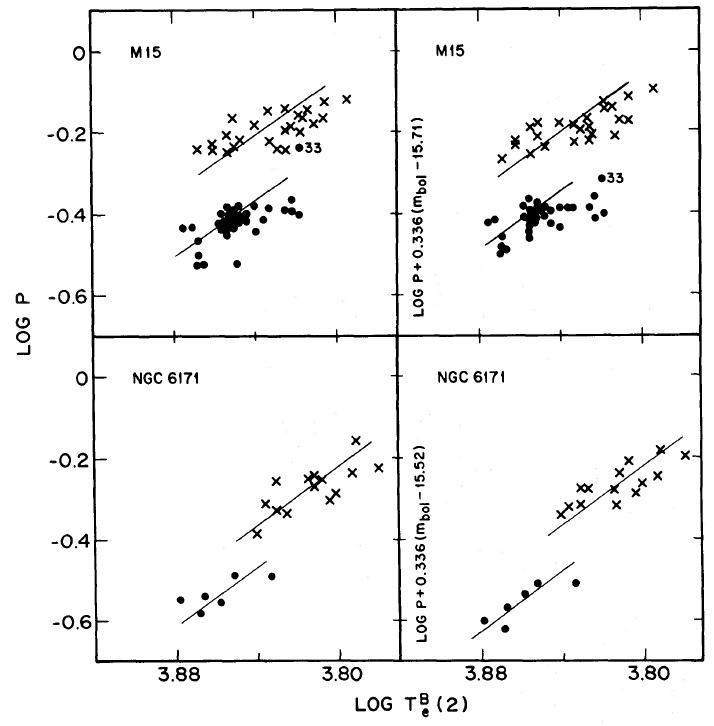図５．左：M15 と NGC 6171 のreduced-周期-温度関係。右：観測周期使用。 直線は理論的な勾配 3.48 でフィットするよう目で引いた。 　

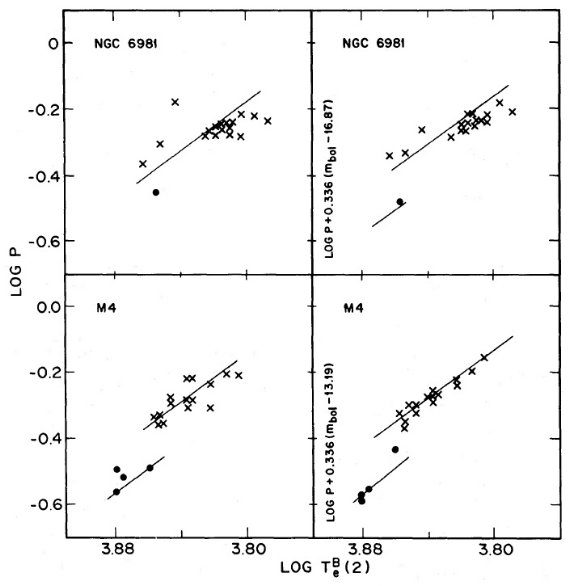図６．図５と同じ、 NGC 6981 と M 4 の関係。 　


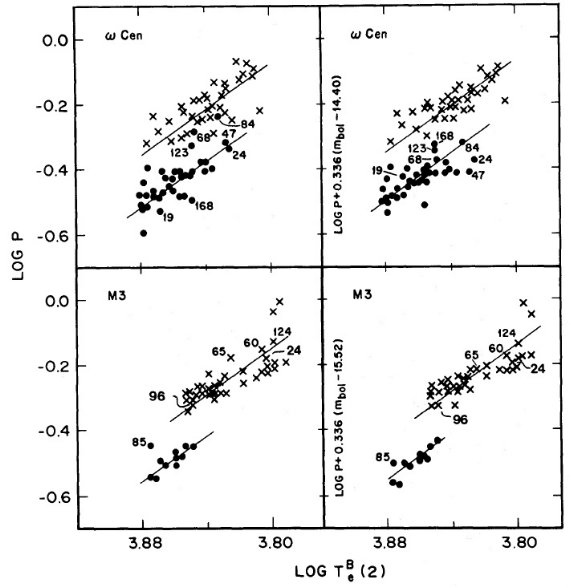図７．図５と同じ。上＝ωCen. 下＝Ｍ５ 　

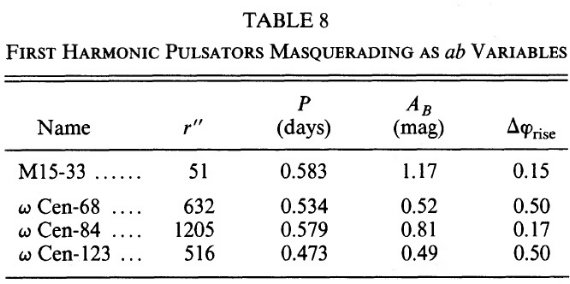表８．第１調和振動星。ab タイプを真似ている。

　　

　　

　

　　

　

　　

　 		　　

　

　　

　

　　

　



図．

　５．M 3 と ω Cen のＰ−Ｌ−Ａ関係　


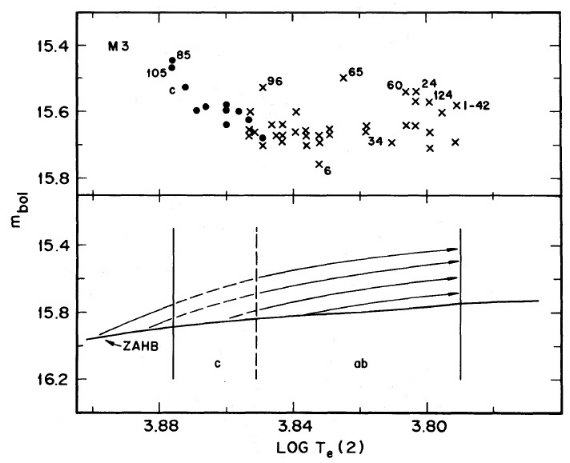図８．上：M3 変光星の mbol - log Te 関係。白丸＝タイプ c. バツ＝タイプ ab.
下：ZAHB からの４本の進化経路の漫画。 　

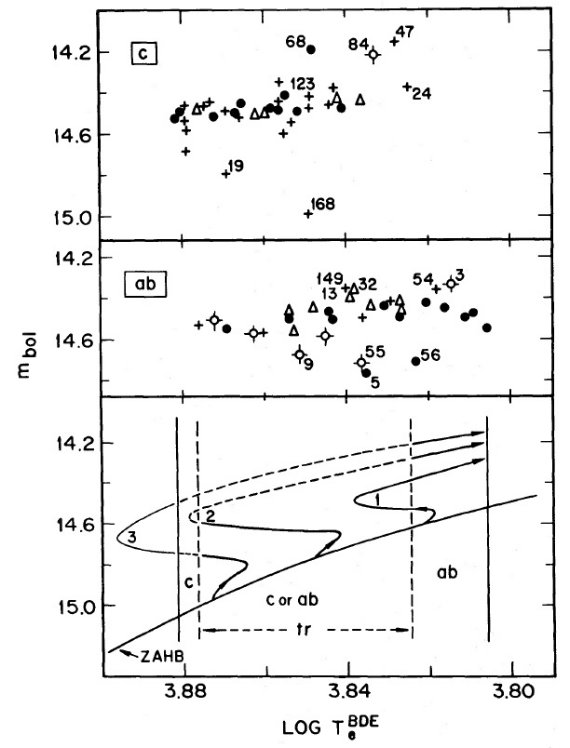図９．図８と同じだが、ωCen の例。上二つの枠：タイプ c と ab を 別々に描いた。十字付き白丸は [Fe/H] = [-1.1, -0.5]. 三角は [Fe/H] = [-1.6, -1.1]. 黒点は [Fe/H] = [-2.0, -1.6].十字はメタル量不定。
下枠：ZAHB からの進化経路の漫画。破線＝タイプ c 領域。モード変化に ヒステリシスがあると、タイプ c と ab とで Te が重なる。 　

　明るい変光星は周期が長い　

　同じ有効温度で見ると明るい変光星は周期が長いはずである。このテスト を M 3 と ω Cen で行ったのが図８である。図の上枠は M 3 の不安定帯 を示す。光度が大きい数個の星の番号を示した。実際これらの星は図７の 左側では点の上縁付近にあり、整約周期に対する右枠では混ざっている。 明るい星 96,65,60, 24,124 は図７では整約周期では小さくなって 混ざり合うのである。 		　図９＝ ω Cen　

　図９では同様のテストを ω Cen　に対して行った。ただし、タイプ ｃと ab の温度が重なっているので、二つを分けて示す。


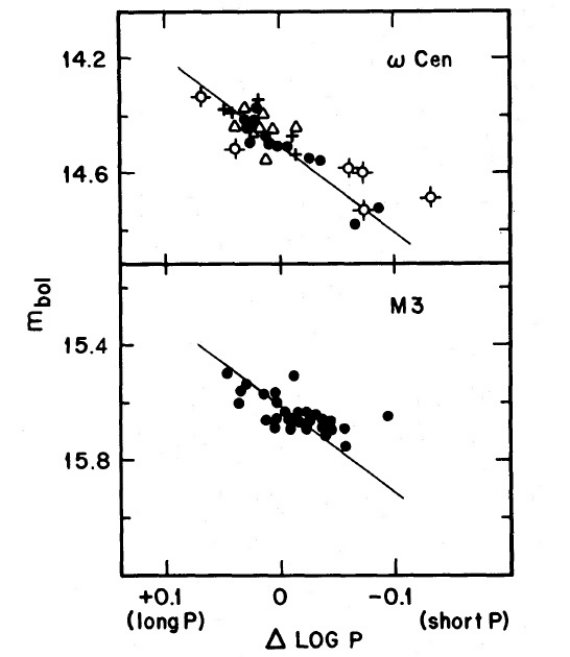図１０．輻射等級と周期シフトの相関。上＝ωCen. 下＝M3. 　

　　

　図１０には周期残差と見かけ等級の関係をプロットした。 周期残差は個々の星の周期の、平均周期・振幅関係からのズレとして定義した。 これは、図５、７の周期・温度関係より分散が小さい。

　　

　

　　

　

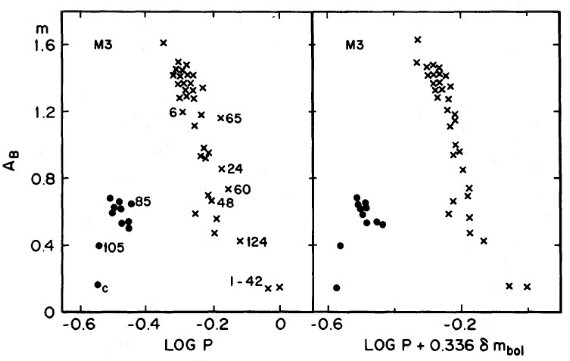図１１．M3 の振幅-周期関係。左＝観測周期。右＝reduced 周期。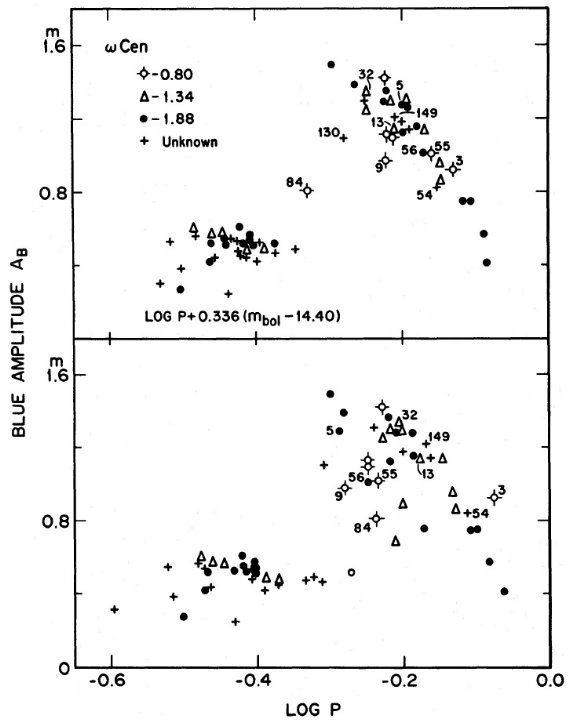 　


図１２．図１１と同じだが、ωCen. 　

　　

　　

　

　　

　

　　

　 		　　

　

　　

　

　　

　



図．

　　

　　

　

　　

　

　　

　 		　　

　

　　

　

　　

　



図．