|
M15 内の 60 RR Lyr 星の3色測光から、不安定帯内でのカラー、振幅、変光
曲線の形、周期の分布を調べた。この Oosterhoff II 型星団に対する、周期-
振幅、周期-増光時間、周期-カラー、カラー-振幅関係を、Oosterhoff I 型星
団 M3 と較べた。 M15 においては、周期を含む相関関係がすべて Δlog P = 0.055 長い 方にシフトすることが判った。一方、振幅-温度、増光時間-温度関係は両者で 一致した。Ritter の条件 P⟨ρ⟩1/2 = Q と両立する 説明は M15 水平枝が M3 より ΔLHB = 0.090 明るいという ものである。 |
ゼロエイジ水平枝モデルを用いて、ΔY = Y(M15)-Y(M3) = +0.05±
0.02 であることが判った。これは、Δlog Z = log Z(M15)-log Z(M3) =
-0.5 とは逆センスである。 M3 と M15 の年齢は、両者の推定年齢の 0.5 σ 内で一致する。低メタ ルほど水平枝光度増加という傾向は、同年齢でメタル量が異なる二つの星団では 低メタルほど主系列ターンオフ光度が明るく、同じである。 M3, M15 の平均年齢はイエールモデルを用い、t = 16.4±3.3 Gyr である。 |
| Oosterhoff 1939, 1944 は球状星団の RR Lyr の周期がはっきりした二つの グループに分かれることを見出した。そこで、低メタルの Oosterhoff II グ ループに属する M15 の RR Lyr を観測して、Oosterhoff I グループ星団 M3 と較べた。 | この論文では M15 データとその解析を示す。連続する論文、 Sandage et al. (1981b), Sandage et al. (1982a), Sandage et al. (1982b), で他の星団のデータ と比較する。 |

|
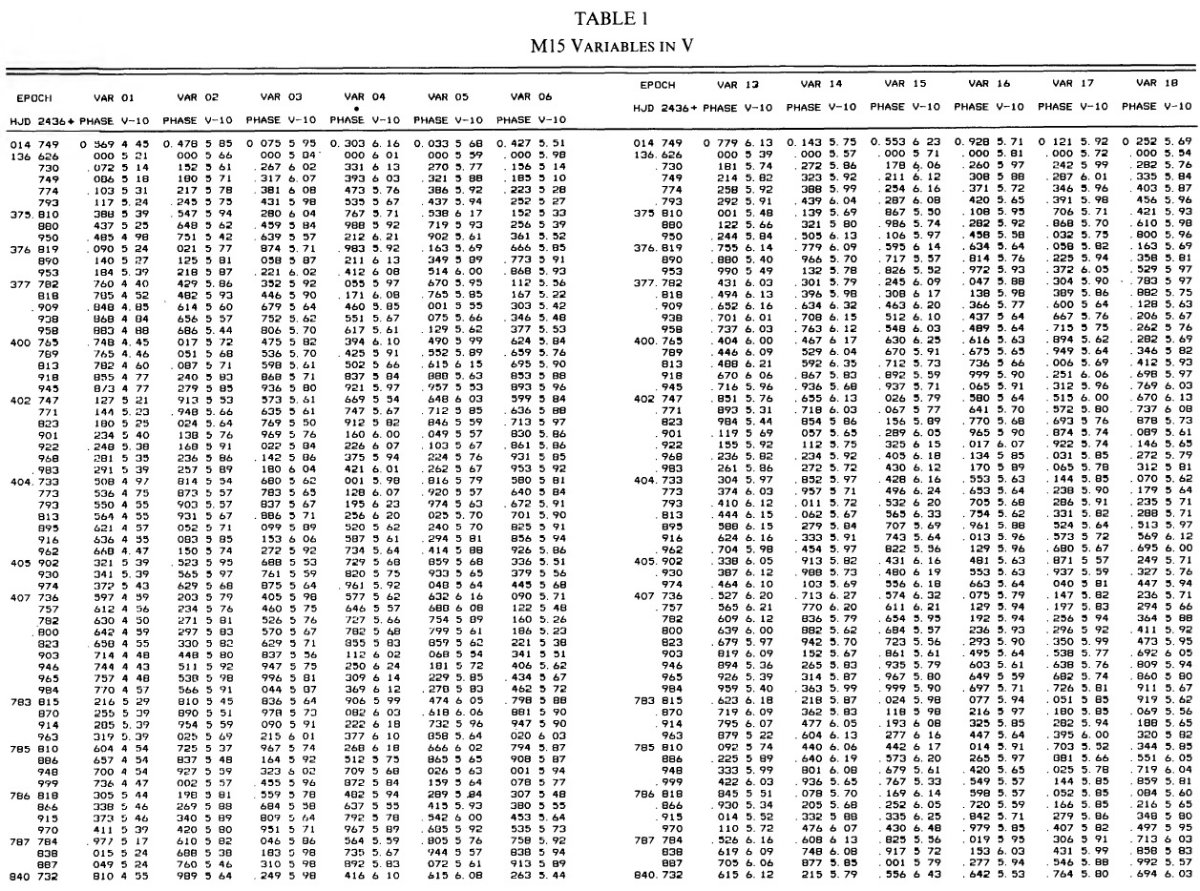
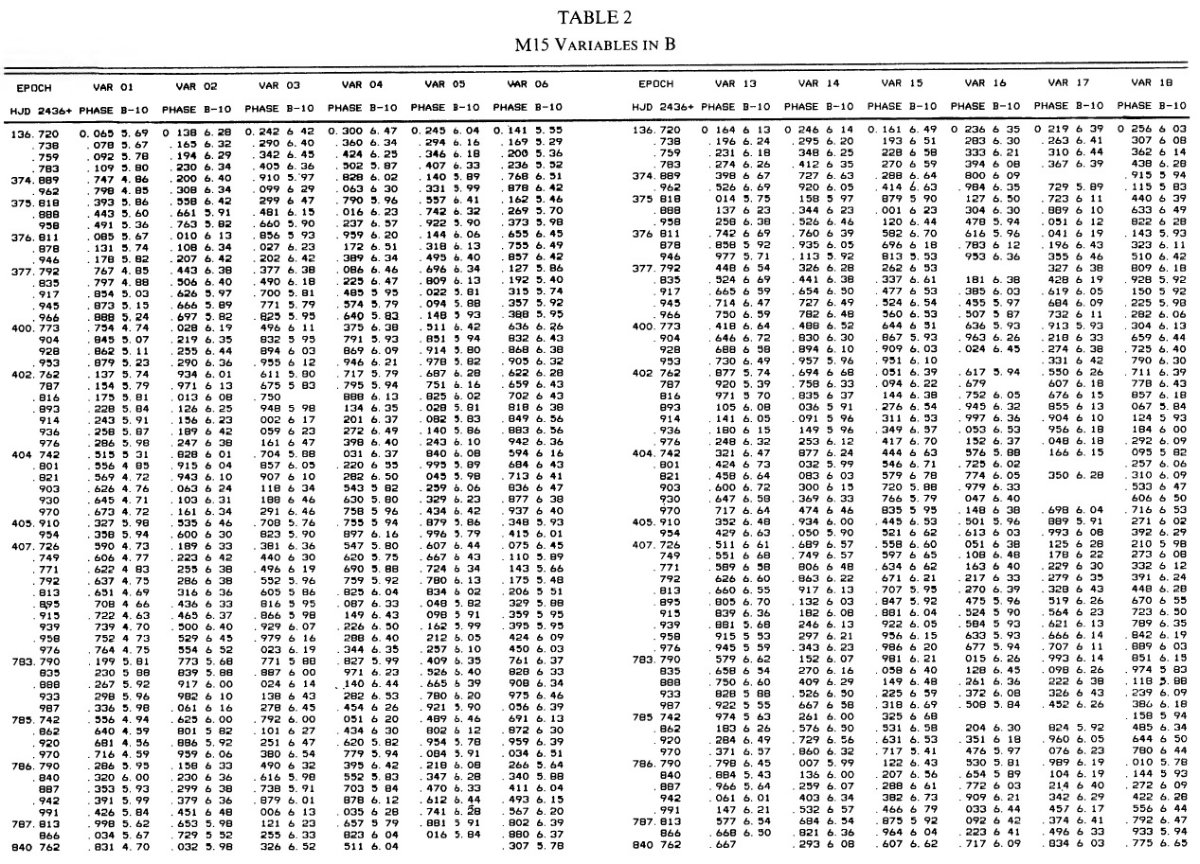
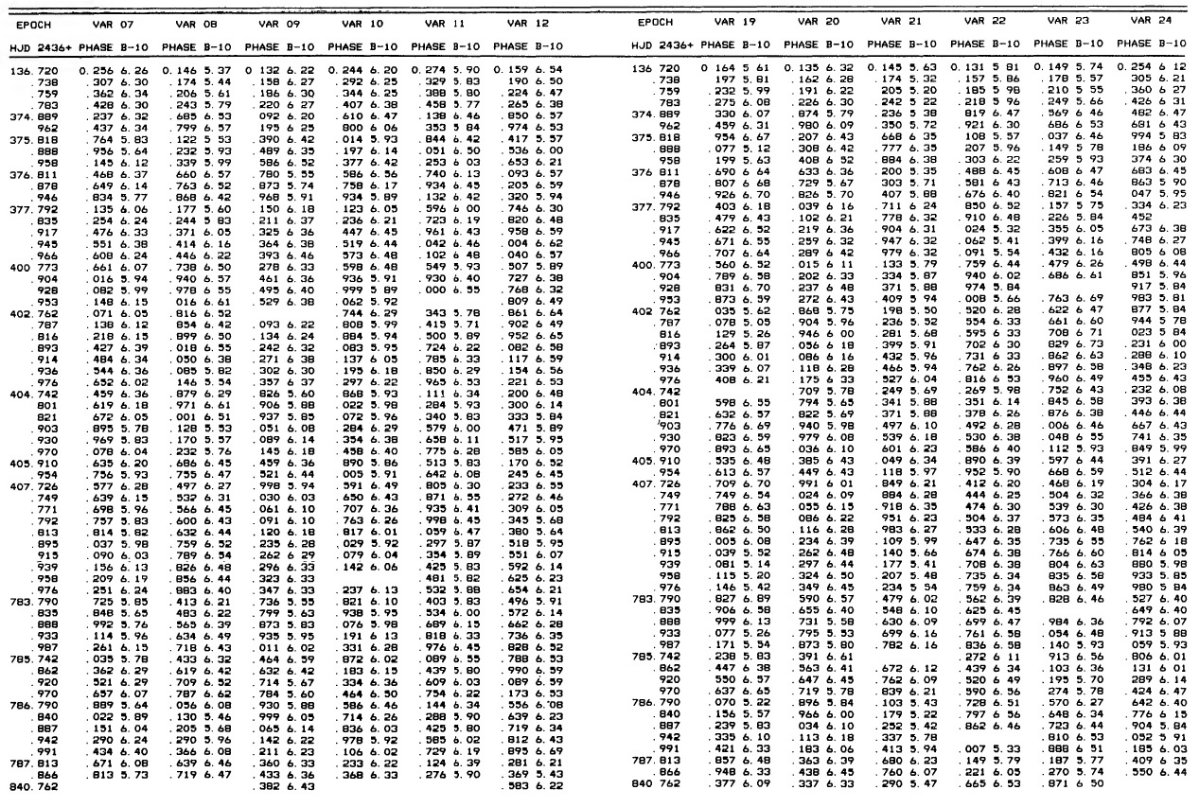
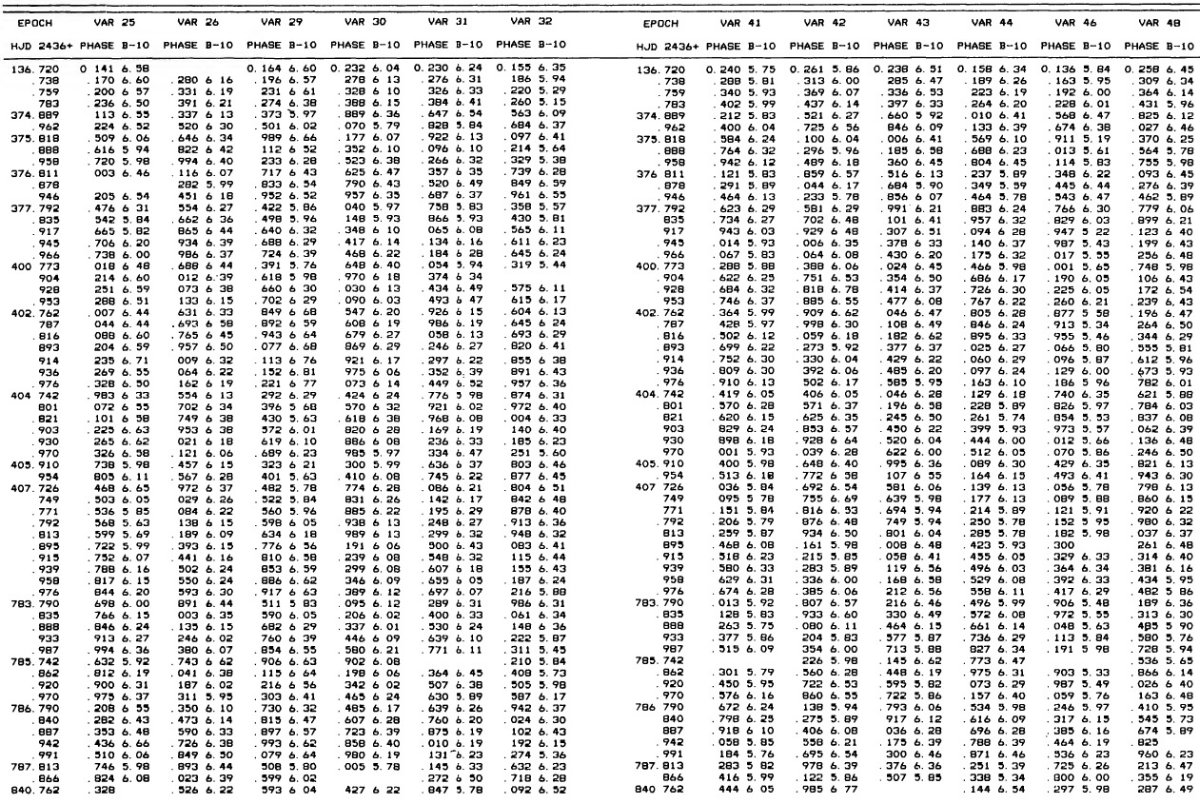
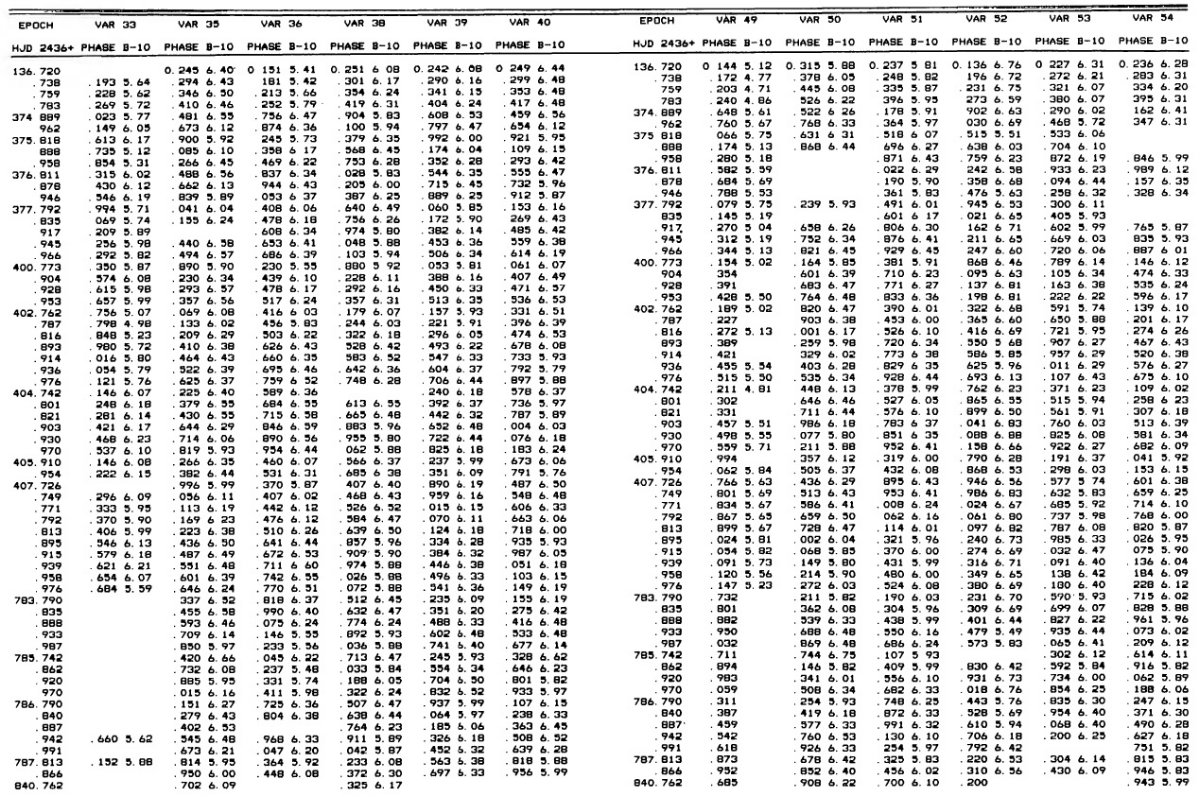
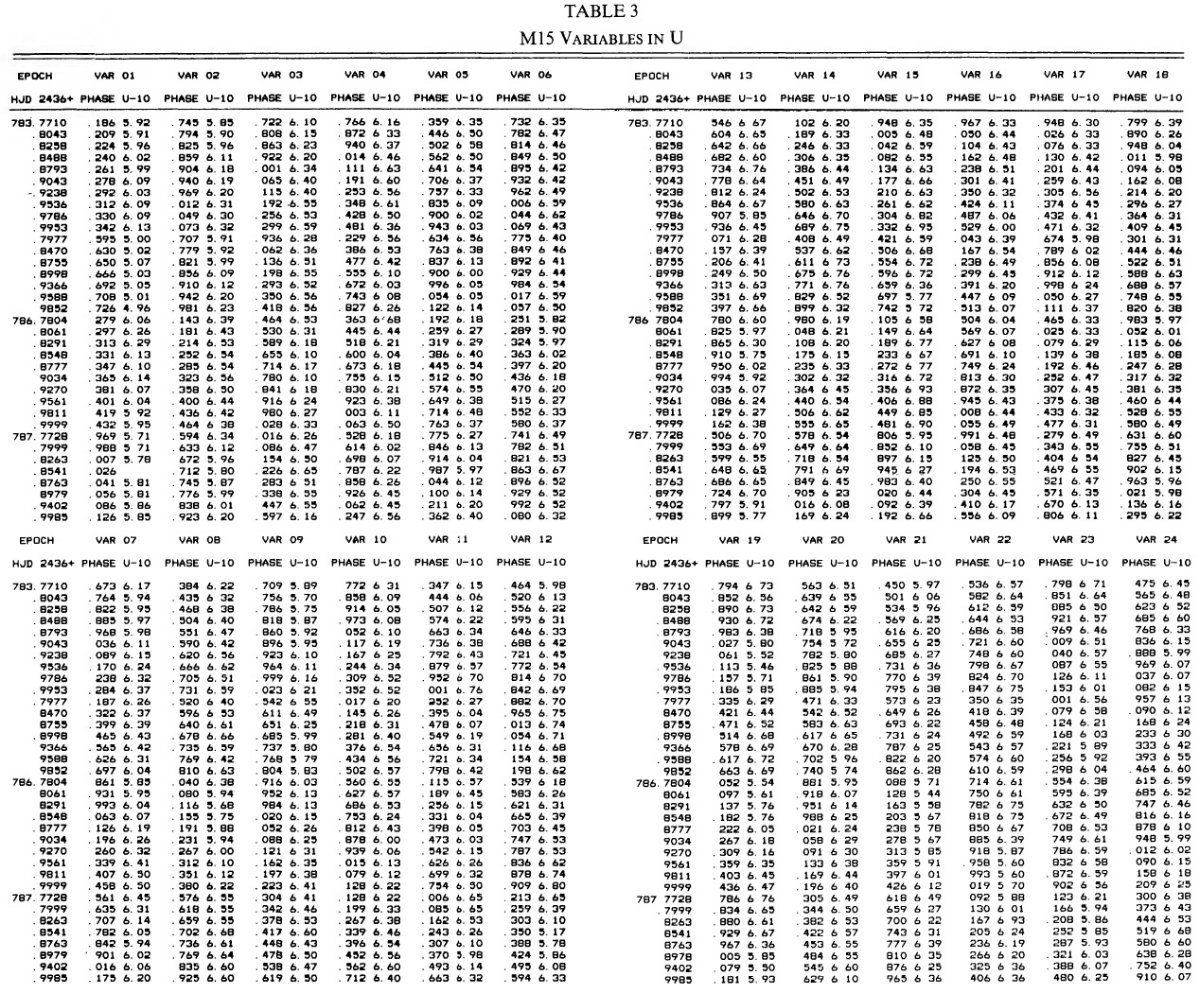
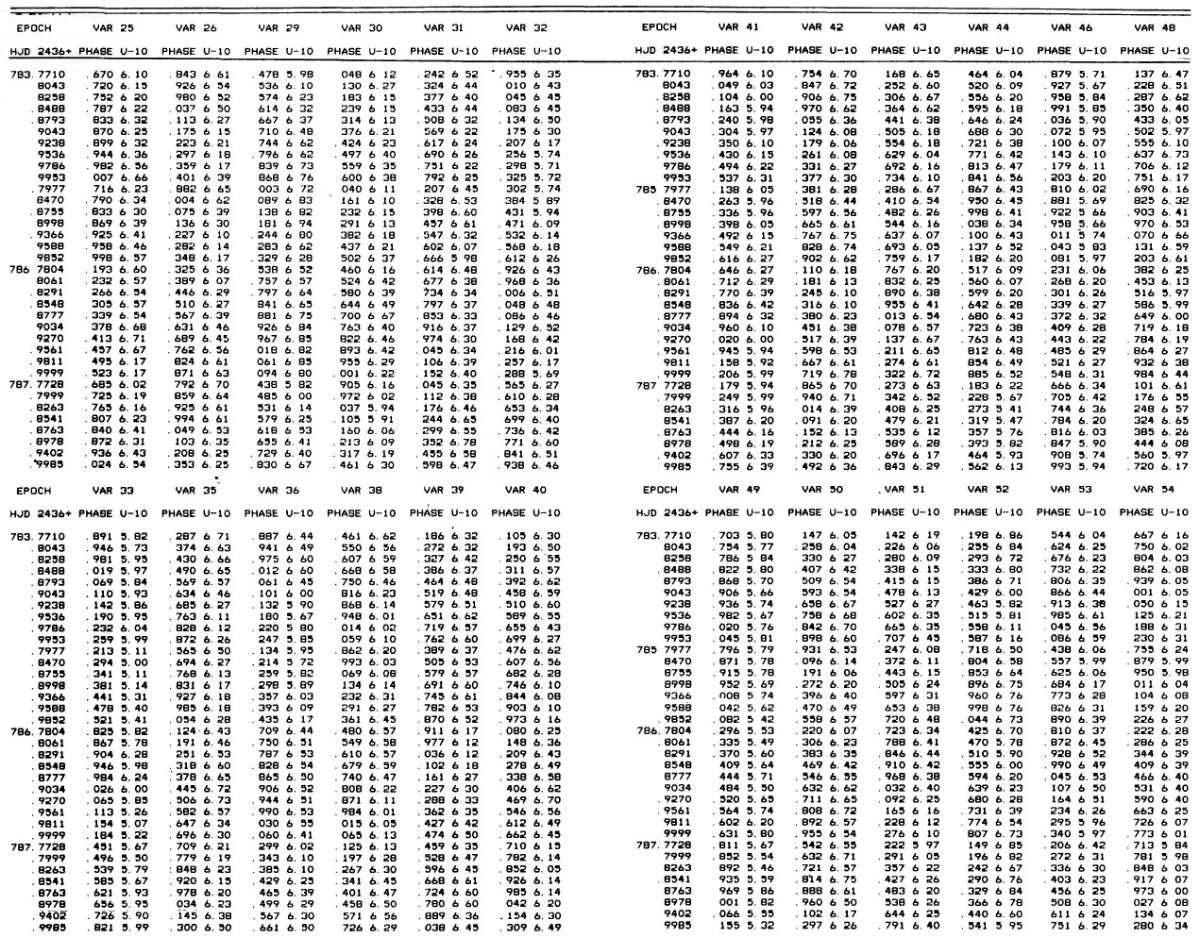
乾板 ウィルソン山 2.5 m 望遠鏡で観測が 1957 - 1959 年に行われた。B (IIa-O+GG13) で 61 枚、V (103a-D+GG11) で 64 枚、U (103a-O+UG2) で 39 枚の乾板が得られた。 |

 |
 |
 |
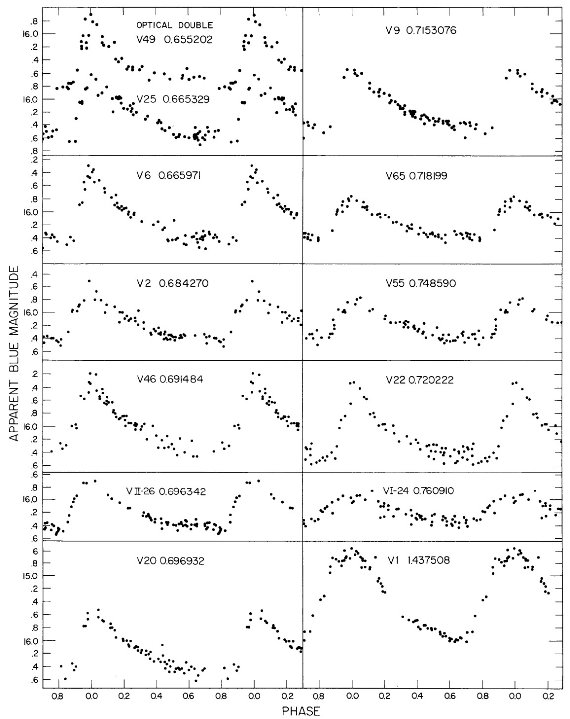 |
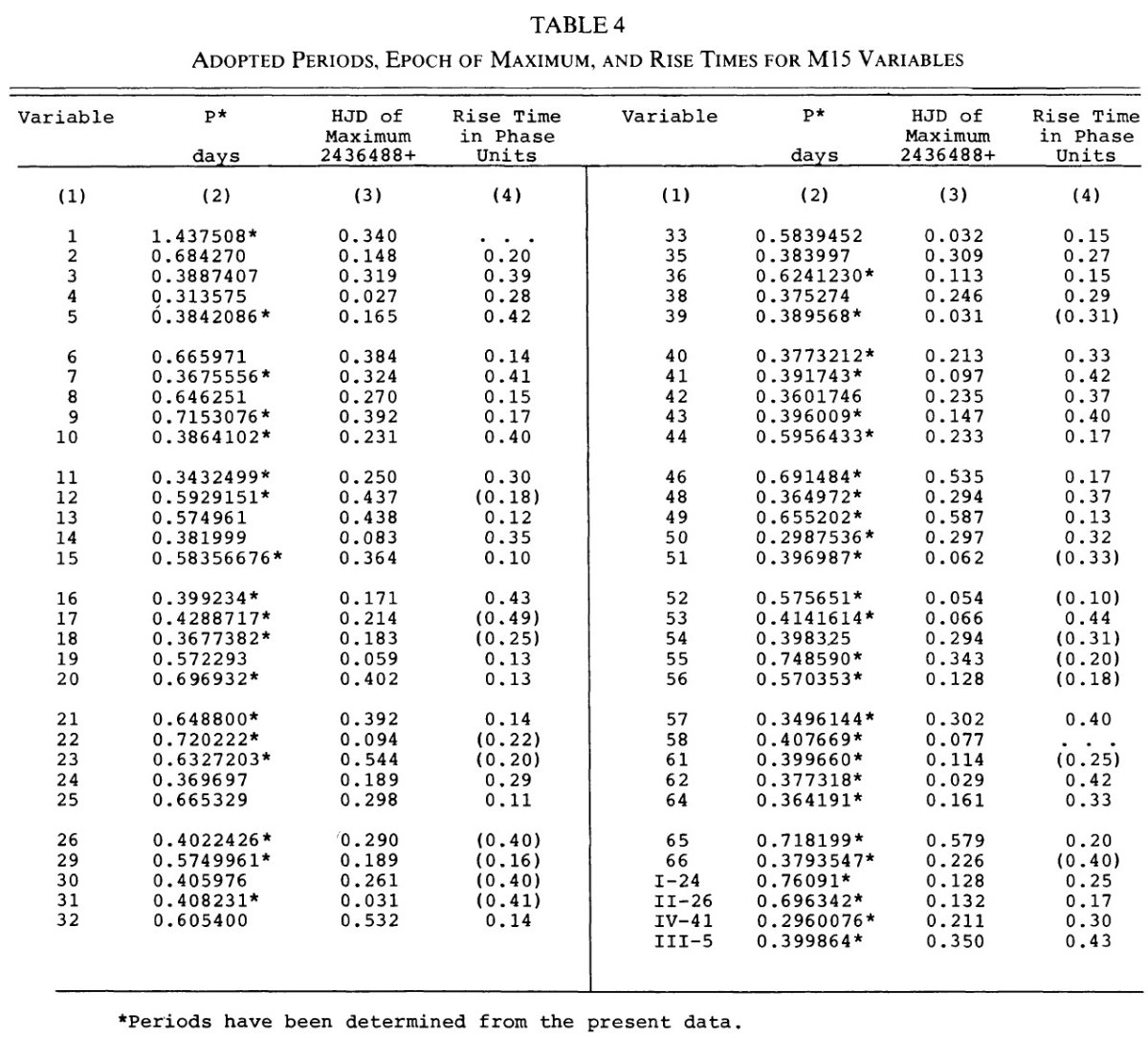
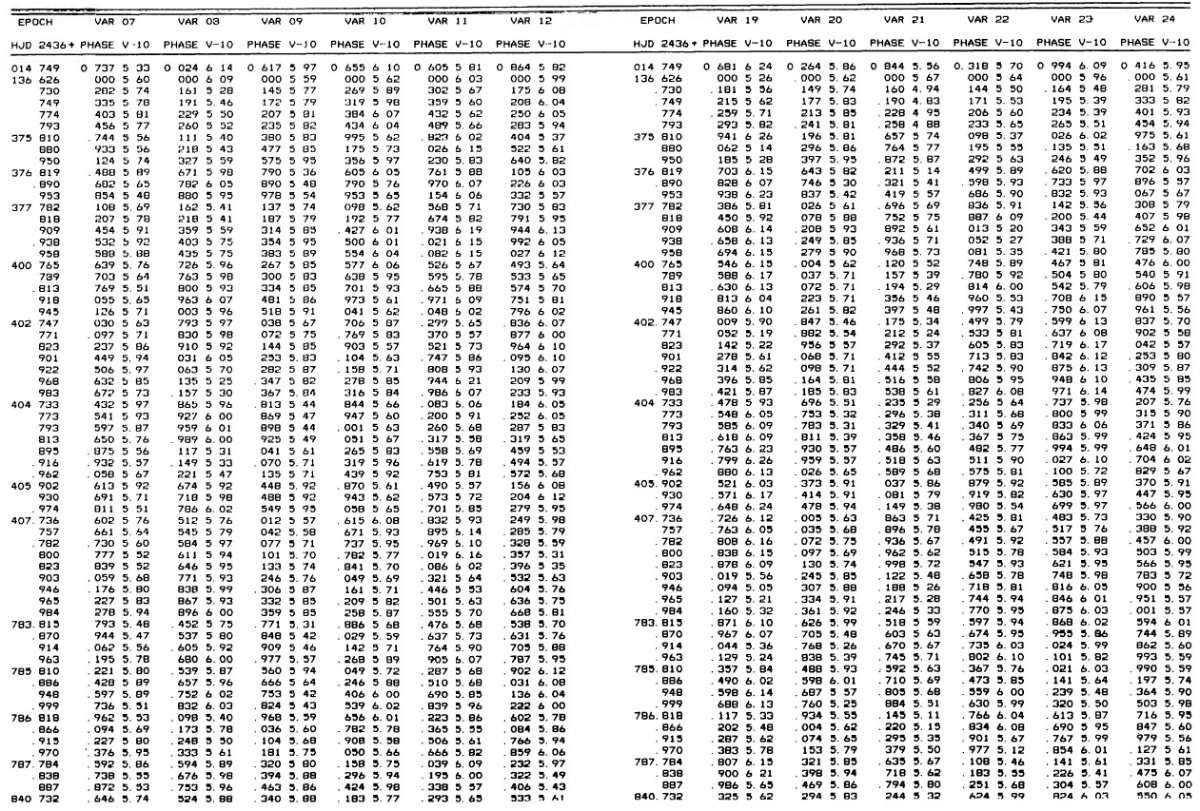
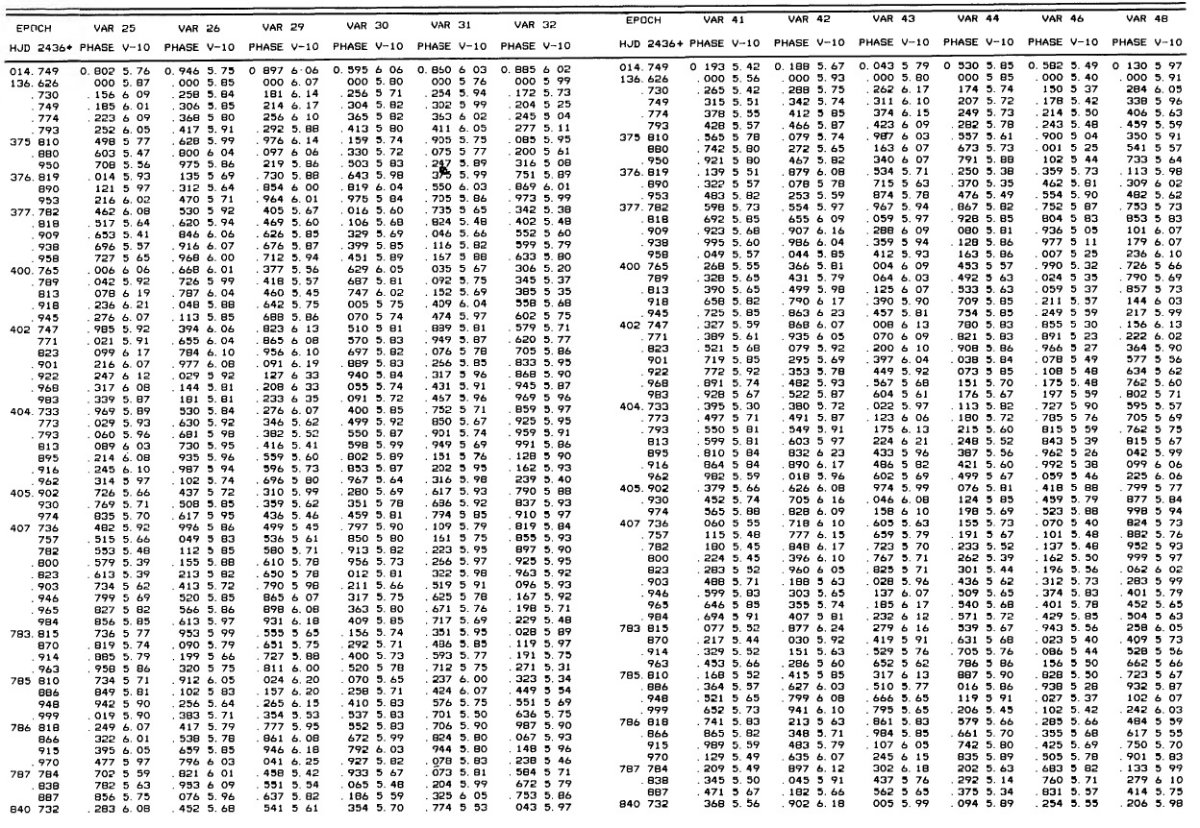
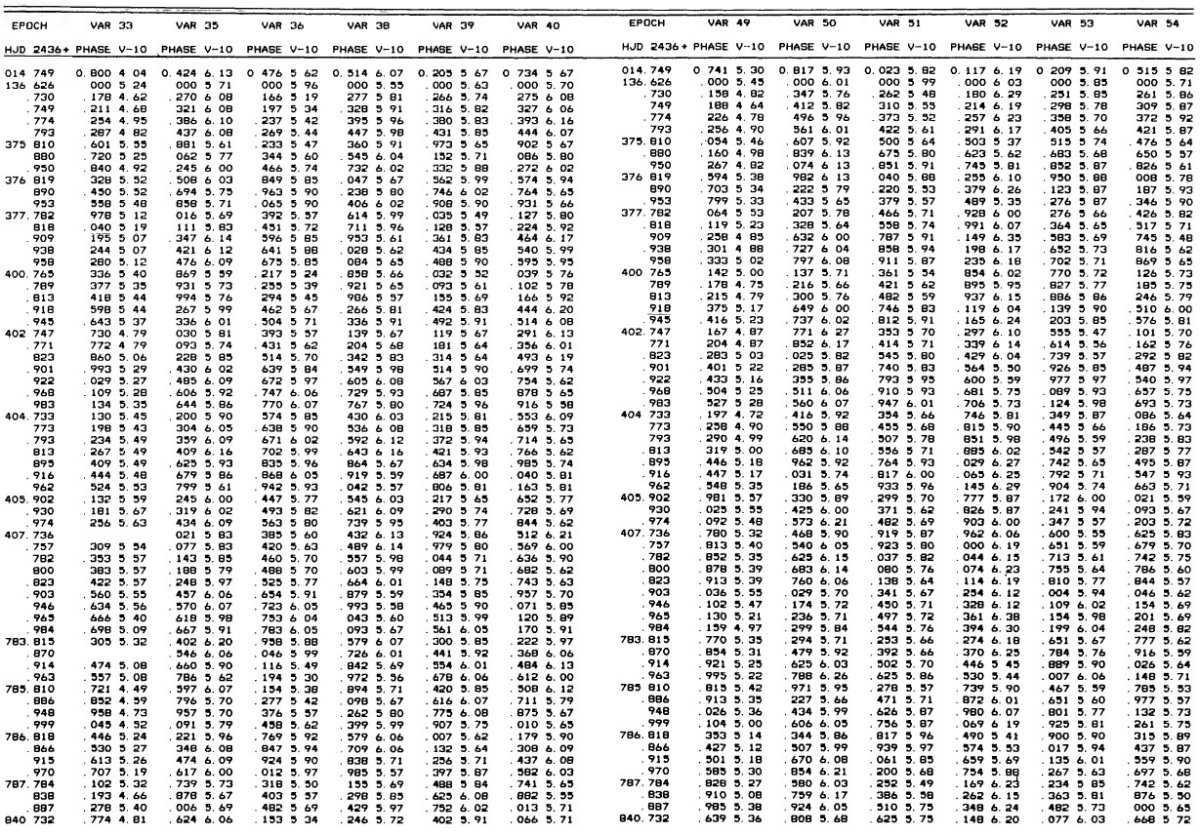
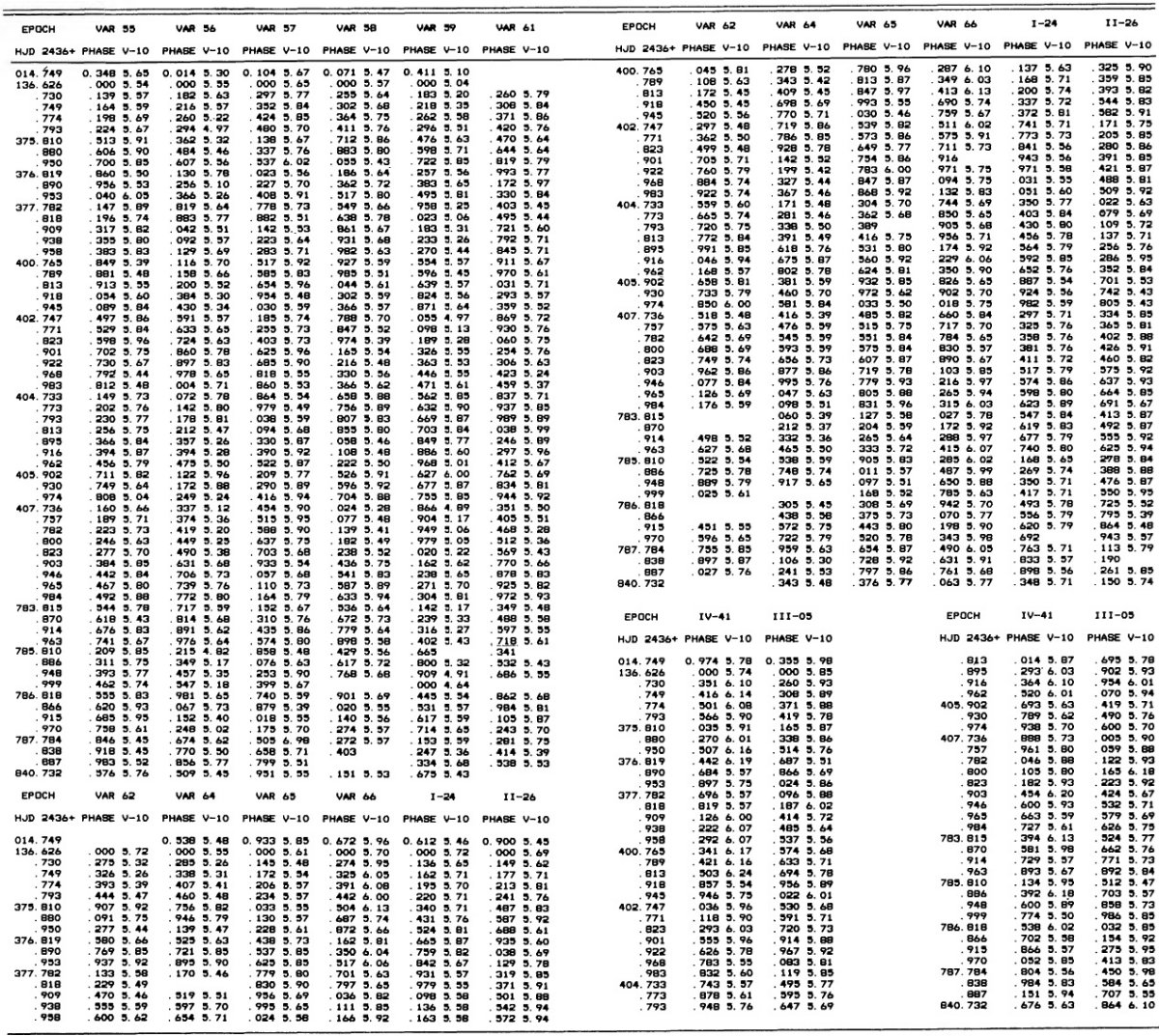
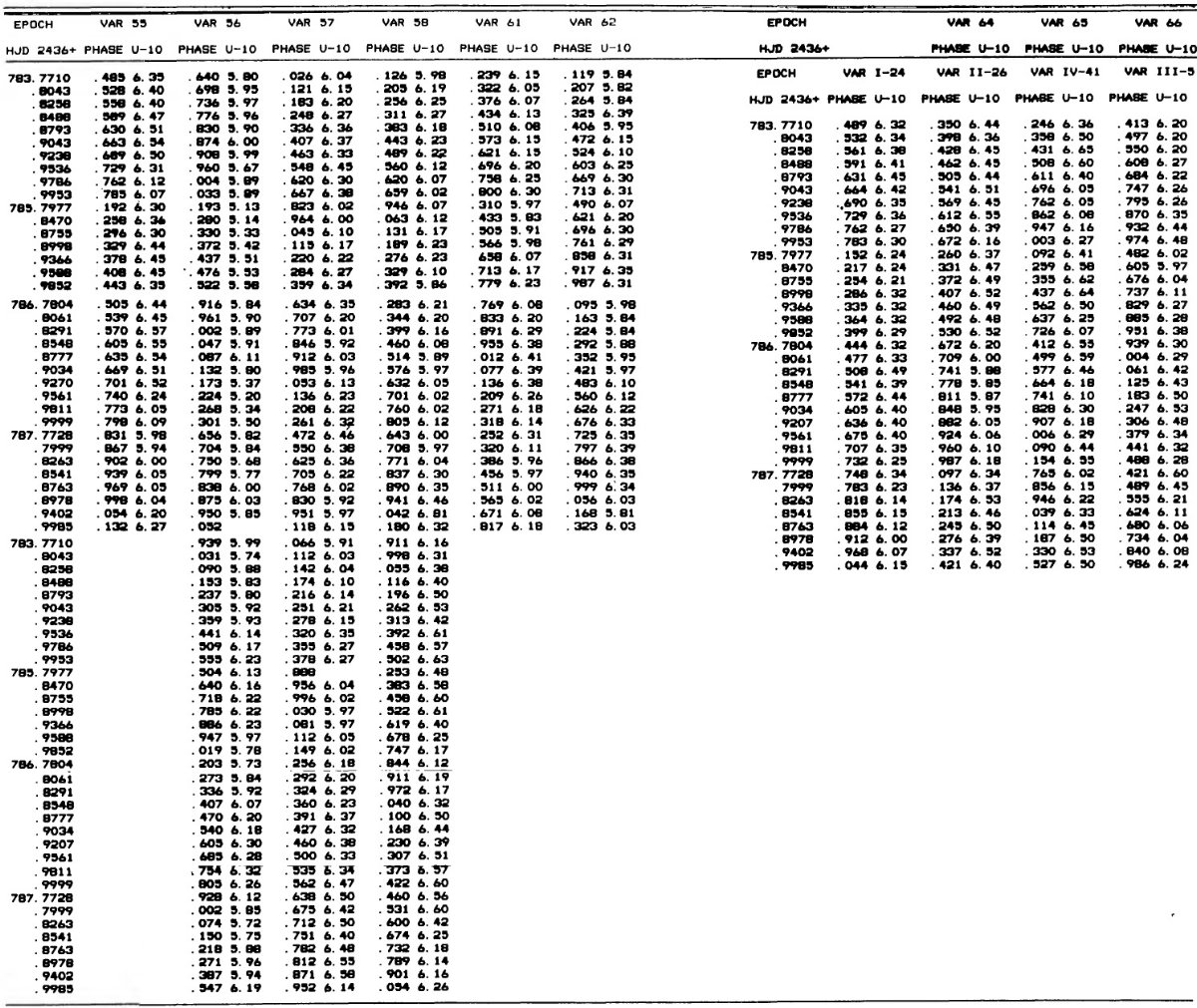
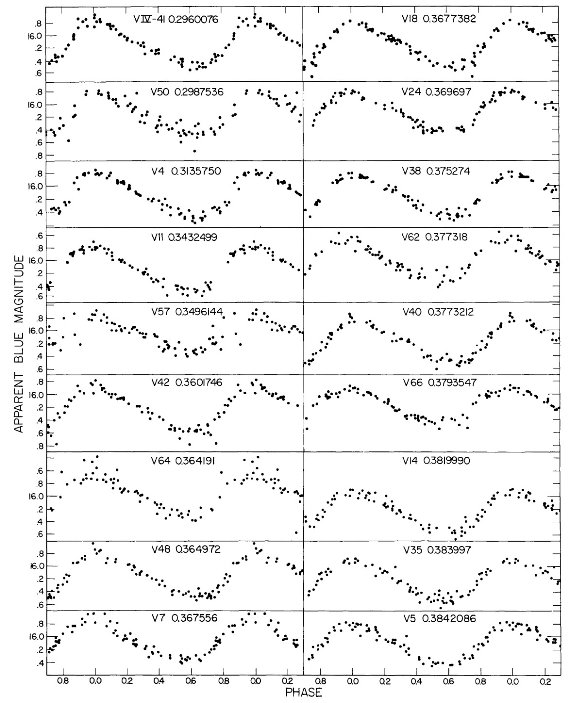
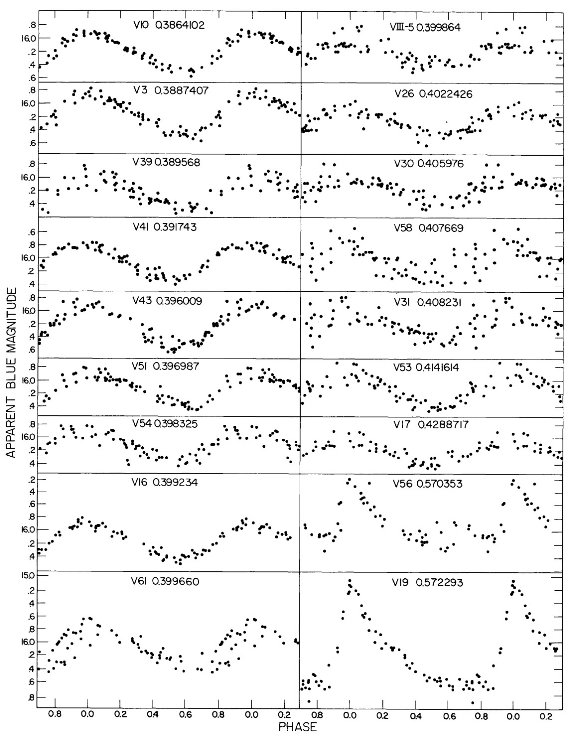
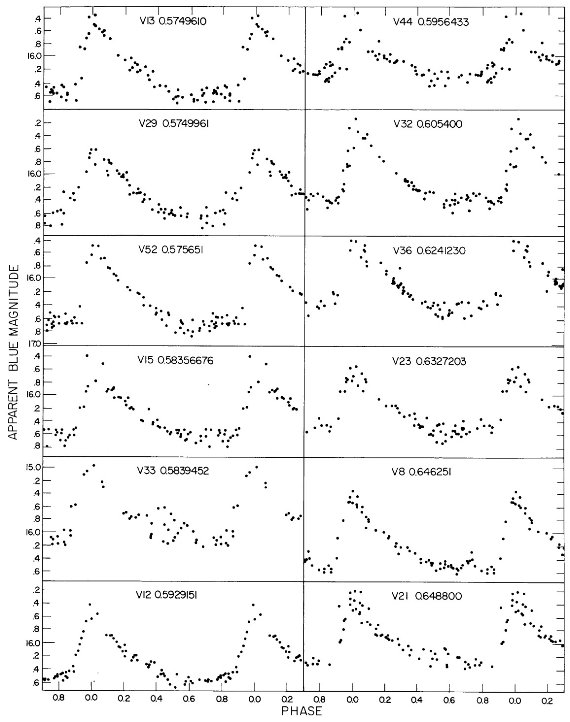
3.1.変光曲線、周期、極大日、増光期間比表4=新しいパラメタ―Hogg 1955, 1973 の周期は怪しいので新しく周期を決め直した。その結果は 表4の第2列に載せた。第3列には極大日を ±0.02 位相単位で与えた。 これは P = 0.5 d に対し 12 分に当たる。極大日は JD 2,436,488 の間で 与えたが、それは 750 日の観測期間の中間である。 増光期間比 増光期間比 Δφrise は表4第4列である。Bailey タイプ c では変光曲線はサインカーブ的で Δφrise = 0.5 であるが、タイプ ab になると、Δφrise = [0.08, 0.25] になる。Δφrise は P とよく相関する。 この関係は論文3で議論するが、 Oosterhoff 群の理解にキーとなることが 分かる。 図2= B バンド変光曲線 図2は B バンド変光曲線である。P = [0.29, 0.36] d の最も短周期の タイプ c 変光曲線は、P = [0.37, 0.40] d のより長周期に比べ、より非対称 で振幅が大きい。この傾向はタイプ ab でも同じで、不安定帯の青縁付近の 最も短周期な星で振幅が最大で、非対称性がきつい。 |
変光の乱れ 図2b で最も興味深いのは、 P = [0.39, 0.429] d という狭い周期帯におい て、突然分散が大きくなることである。この帯内の変光はサイクルごとに振幅 が変わり、位相変光曲線の散乱が大きくなる。この周期帯の巾が狭いこと、そこ がタイプ c とタイプ ab の境目にあることから、この現象は基本振動と第1 倍音振動のモードミクシングによると考えられる。この現象が Oosterhoff 群 I と II とで変わるかどうかは重要である。 3.2.平均測光パラメタ―表5の平均等級変光曲線は等級表示だが、これをフラックス変化に変え、平均フラックスに 直してから改めて平均等級を出した。それらを表5に示す。 表5の平均カラー 表5の平均カラーは平均等級の差として定義したものを示す。 3.3.混入補正図3では、表5の平均カラーと平均等級を星団中心からの距離に対してプロ ットした。中心距離 r = [60", 200"] の間に ⟨V⟩ で 0.2 mag の 変化がある。この変化をフィットして混入補正に使用した。 |
|
表6=表5の混入補正 図3のフィット曲線による補正を表5のデータに施した結果が表6である。 表6の第4−6列には添字 c で補正値であることを示した。赤化 E(B-V) = 0.08 を採用した。 平均カラー 表6の第10列には、赤化と混入効果を補正した平均 B-V カラーを示す。 これは等級表示のカラー変化曲線を積分して平均を取ったものである。 Preston 1961a は、⟨B⟩-⟨V⟩ よりもこのやり方が平均 温度を得るには適しており、Q = P⟨ρ⟩ 関係に入る平均カラー としてはより適していることを示した。この論文では Preston 1961 の 図1を用いて ⟨B⟩-⟨V⟩ から ⟨B-V⟩ へと 変換した。 |
有効温度 T1 表6第11列には平均カラーに対応する有効温度を Bell 1977 の [Fe/H] = -2 に対するカラー対温度関係を用いて示す。関係のまとめは Butler, Dickens, Epps 1978 から採った。 有効温度 T2 ただ、純粋に経験的な観察であるが、カラー・等級関係、カラー・周期関係では カラーの位相平均よりも平均等級間の差としてのカラーの方が分散が小さい。 そこで、表5のカラーを使った有効温度を T2 として第12列に載せた。 |
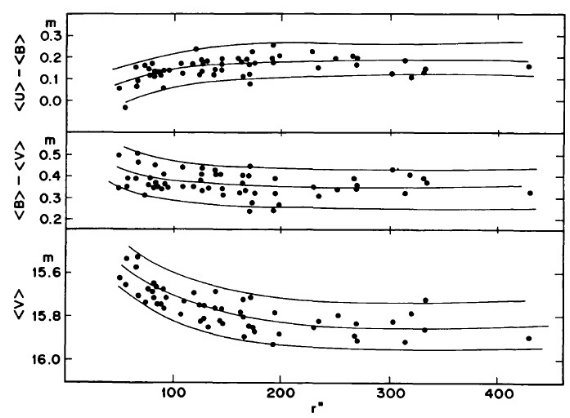 図3.平均等級とカラーの星団中心距離効果。周辺星の混入による。 |
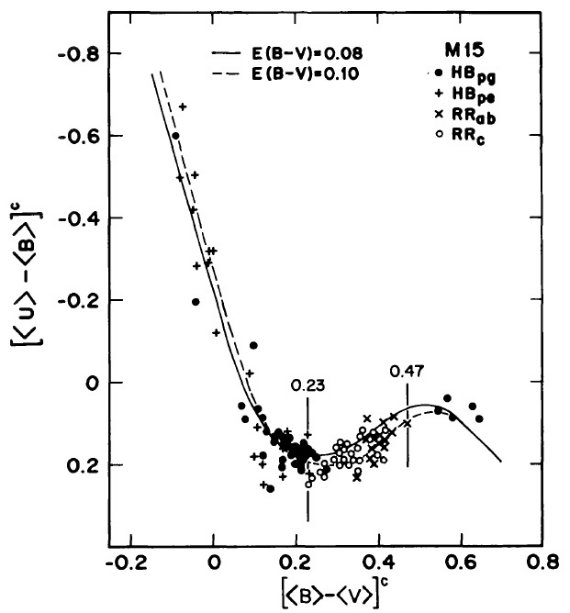 図4.M15 の HB 星と変光星の二色図。不安定帯のカラー端 を示す。 |
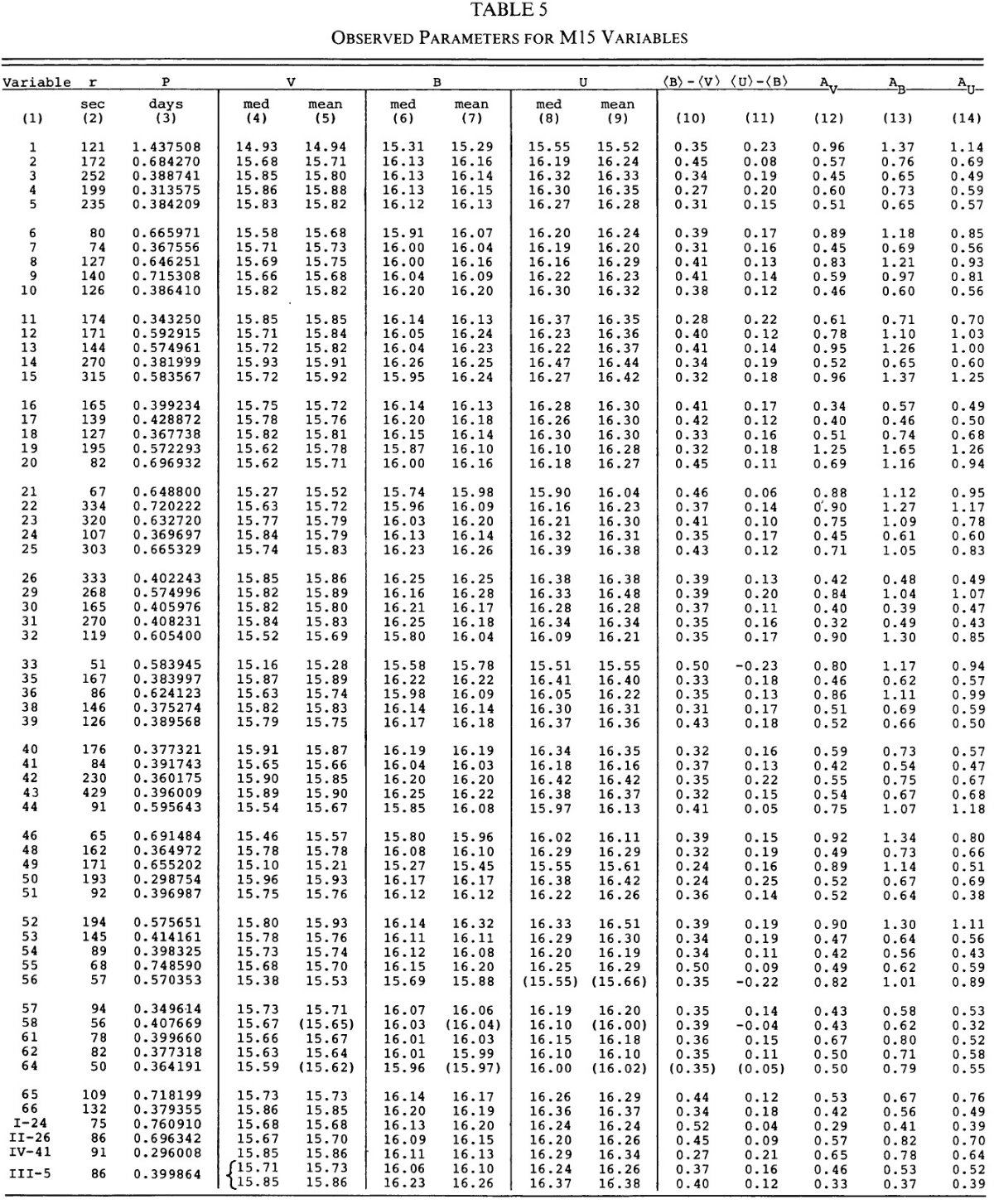
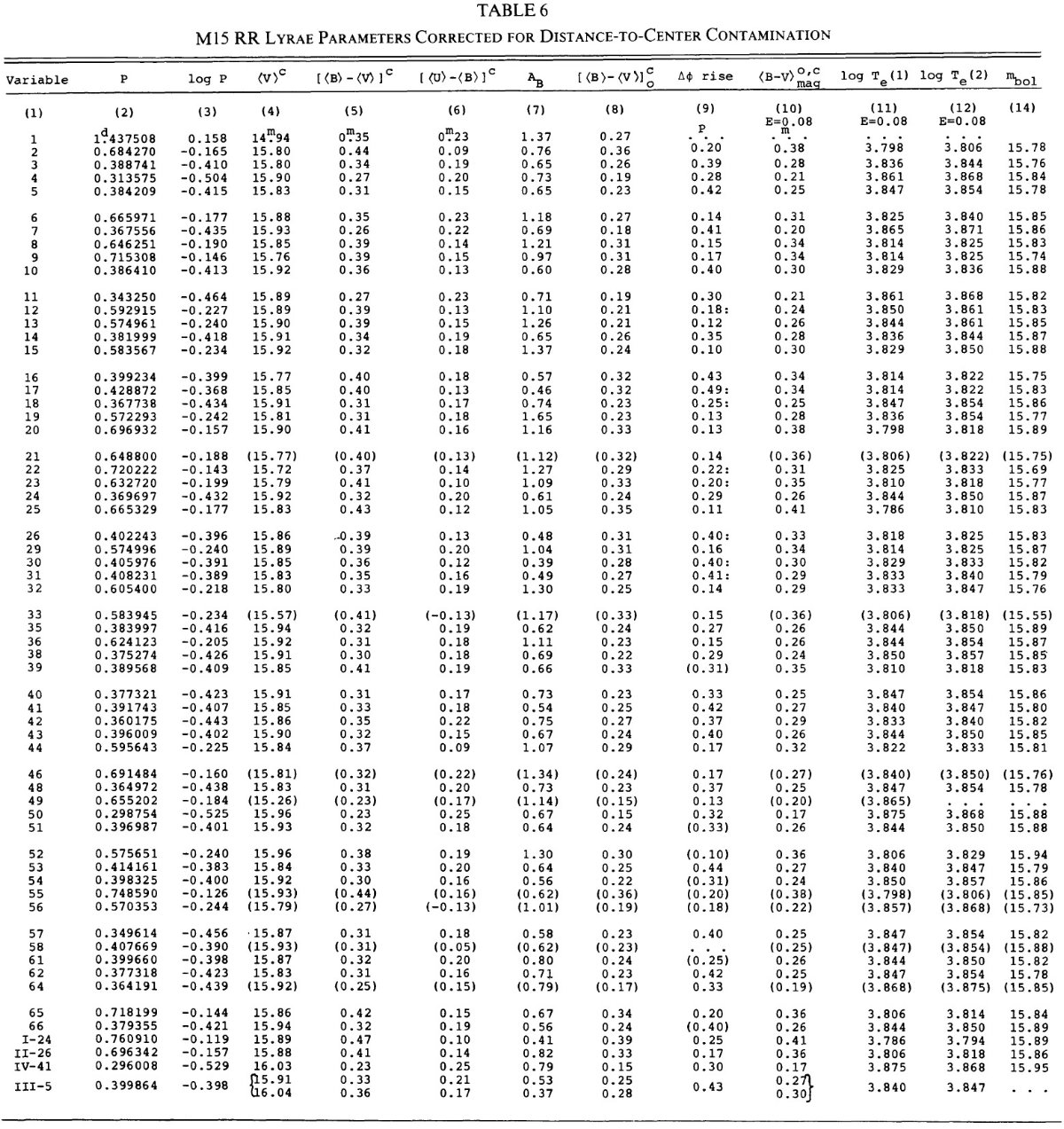
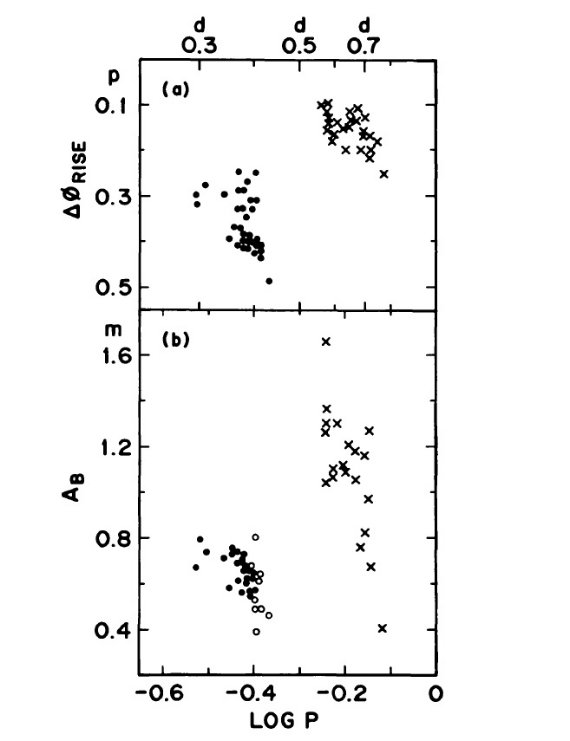 図5.増光期間比と青振幅の周期との関係。バツ=Bailey タイプ ab. 黒丸=タイプ c. 白丸=ミックスタイプ 図5b =周期と振幅の関係 図5b は表6に載った M 15 変光星の周期と振幅の関係を示す。黒丸=タイ プ c, バツ=タイプ ab、白丸=ミックスモードである。タイプ ab の基本振動 の青端が P = 0.570 d にあり、そこで振幅最大になることが明らかである。 周期が長くなると共に振幅は小さくなり、P = 0.760 d で AB = 0.4 mag となる。タイプ c においても同様の振る舞いが観察される。第1倍音 振動の青端 P = 0.298 d で振幅は最大で、長周期側に行くに連れ振幅は減少 する。 |
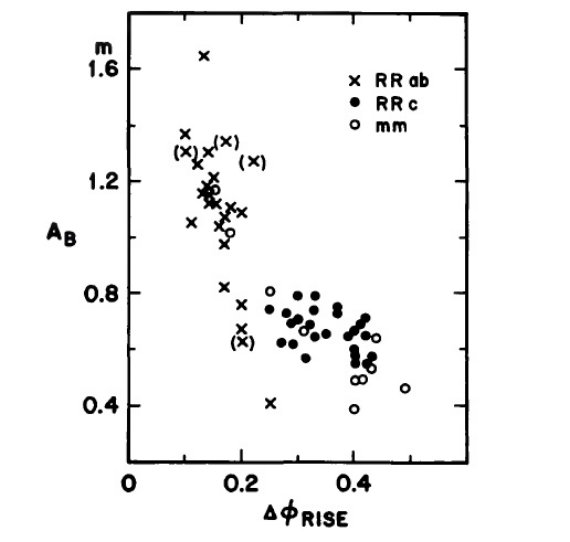 図6.青振幅と増光時間割合の相関。 図5a =変光曲線の形 図5a は変光曲線の形が周期と共に変わっていくことを示す。Δφ セファイドの場合 古典セファイドでも同様の傾向が見られる。ただ、フィールド星であるため 赤化や光度の不確定さのために直接の観測的証拠を得ることが難しい。LMC で はこの問題が小さい。 非線形効果 図5a と b の形が似ていることは、つまり、振幅と形にも相関があることを 意味する。両者の関係は図6に示す。一般には、小振幅ほど変光曲線は対称的 になる。振幅が大きくなると、非線形効果が働き、振動系が Van der Pol 緩和 振動的になり、変化がサインカーブから外れて行くのである。 |
5.2.周期・カラー関係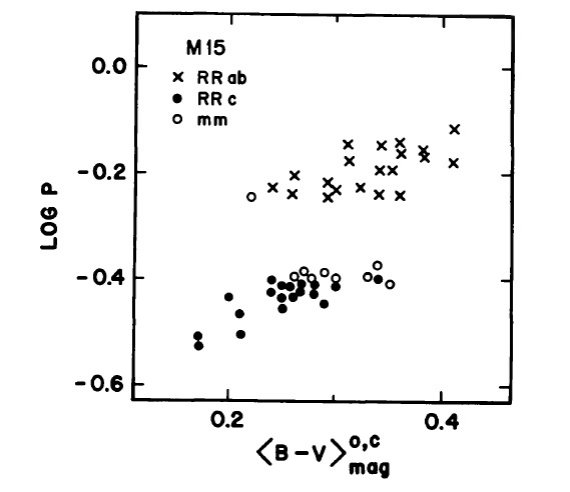 図7.周期と平均カラーの関係。 カラーの重なり 図7に完全に補正された ⟨B-V⟩o,C と周期の関係を 示す。⟨B⟩-⟨V⟩を用いても同様だが、最も目立つ特徴は タイプ c と ab のカラーが重なることである。この重なりは Oosterhoff I 型 星団の M 3, M4, NGC 6171 では見られない。ところが II 型の ω Cen にはカラーの重なりが生じている。 重なりの一般化 現在のデータでは Oosterhoff 群によりカラーの重なり方が異なるのは、 タイプ c と ab の間の温度境界が Oosterhoff 群によって異なることを意味 すると一般化するには不十分である。しかし、これが水平枝進化における 何か未知のパラメタ―による効果を明らかにするキーかも知れない。 |
5.3.カラー・振幅関係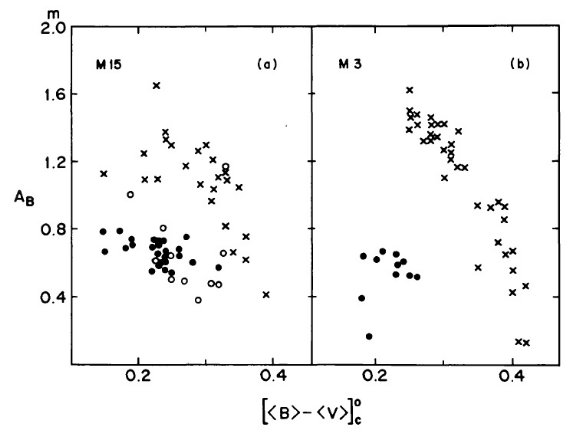 図8.カラーと振幅の関係。左=M15. 右=M3. バツ=Bailey タイプ ab. 黒丸=タイプ c. 白丸=ミックスタイプ. タイプ c と ab のカラーの重なりは M 15 で目立つが M3 ではない。 図8=カラー・振幅関係 図8のカラー・振幅関係ではタイプ c と ab 間の重なりがより鮮明に表現 されている。ここでは完全補正の [⟨B⟩-⟨V⟩]oC を用いた。M3 にはカラーの重なりがない。 M 15 にはある。 温度・振幅関係はシフトなし 図8の M3 と M15 プロットを見ると、 M 15 のタイプ ab のカラーを赤い 方に 0.03 等動かすと M3 に重なることが判る。これは、Preston 1961 が 微分ブランケッティングとして予想した大きさなので、温度・振幅関係は 量星団間で一致する。図12を見よ。これは Oosterhoff 問題を解く鍵となる。 |
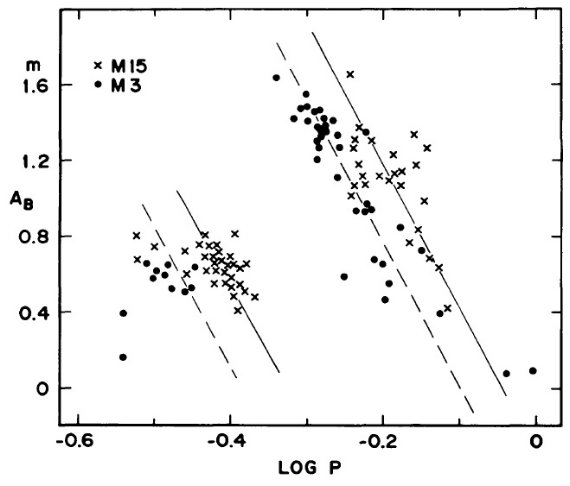 図9.周期振幅関係の M15 と M3 の比較。二本の線は Δlog P = 0.055 に 対応。目で引いた。 |
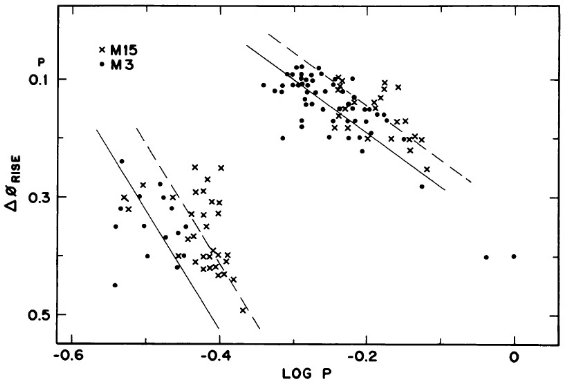 図10.周期-増光期間比関係の M15 と M3 の比較。二本の線は Δlog P = 0.055 に対応。目で引いた。 周期シフト Δlog P = 0.055 図9,10は M 15 の周期振幅関係、周期-増光期間比関係が M3 に対し、 等しい振幅または増光期間比に対して Δlog P = 0.055 ずれていること を示す。これは、 Oosterhoff 効果であるが、ずれが平均値と言うよりは個々 の変光星に対して現れている点が重要である。 |
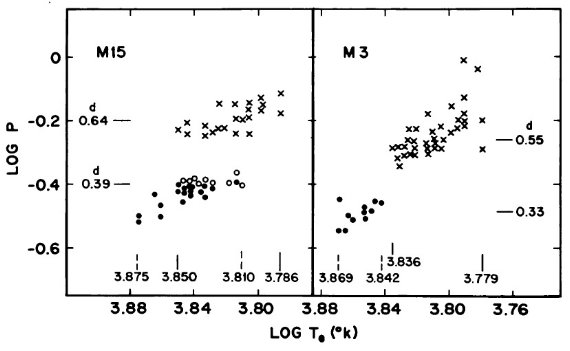 図11.周期温度関係の M15 と M3 の比較。下のバーは温度境界を示す。 バツ=Bailey タイプ ab. 黒丸=タイプ c. 白丸=ミックスタイプ. 平均周期は M 15 で ⟨P⟩c = 0.39 d, ⟨P⟩ab = 0.64 d. M 3 で ⟨P⟩c = 0.33 d, ⟨P⟩ab = 0.55 d である。 周期温度関係の周期シフト Δlog P の意義 図11の周期温度関係は、周期シフトを説明するための、潜在的には最も 強力な道具である。と言うのは、周期と温度は Ritter 1879 の脈動定数 Q を 通じて結び付けられているからである。 Te2 の方が分散小 M3 と M15 では、タイプ c でも ab でも、温度の等しい変光星同士は周期が Δlog P = 0.070 離れている。図11では表6の Te1 を採用した。それは、 Preston 1961 の示唆に従ったからである。しかし、 [⟨B⟩-⟨V⟩]oC に基づく Te2 を使うと、タイプ ab に対しては Δlog P = 0.020 と差 が縮まり、分散も小さくなる。 図12=振幅・温度関係 図12でも Te1 を使用した。タイプ ab では星団 M 15 と M3 が重なり、 シフトがないことが判る。タイプ c では ΔlogTe = 0.01 のシフトが あるが、微分ブランケッティング補正の不定性が原因と考えられるので、 こちらもシフト無しと看做して良い。 |
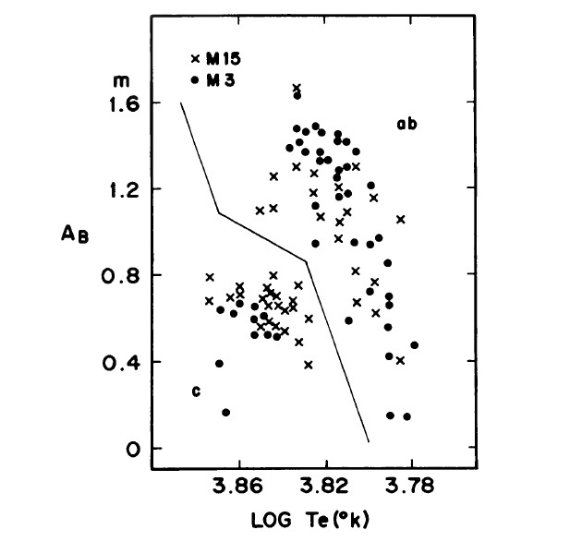 図12.振幅-温度関係の M15 と M3 の比較。タイプ c と ab の境界を実線 で示す。タイプ ab の振幅-温度関係は M15 と M3 で似ていることに注意。 図13=マンガでの説明 光度が異なると考えると、(1)図9、10、11のシフトと(2)図12 でなぜシフトが無いか、が説明が付く。図13bは RR Lyr 付近の HR 図である。 図2には式(4)から導いた、P=一定の線も引いた。図13a には振幅の変化 を略図とした。M 15 を星団 A、M 3 を B とする。P = 0.5 d ラインを考えよう。 この周期を持つ星団 A の星は、星団 B の星より青い。振幅も大きい。この予言 はどちらも同じ周期を持つ一対の星に対するカラーと振幅のシフトの観測結果 と一致する。同じことだが、 同じ振幅または同じ有効温度の星同士に周期 シフトが起きる。最後になるが、もし振幅が不安定帯上での位置で決まるなら、 図13は周期振動関係が二つの星団で一致することを示している。 |
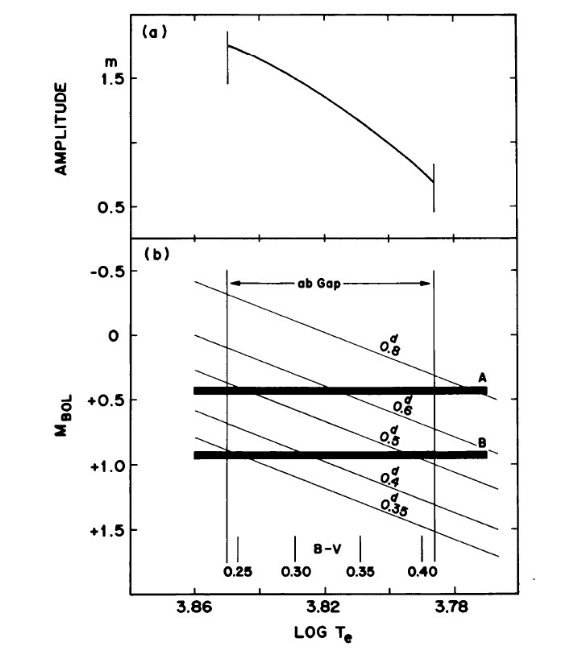 図13.Oosterhoff 周期グループを HB 光度の差で説明する図。 星団A(上の太横線)= Oosterhoff グループ II (M15). 星団B(下の太横線)= Oosterhoff グループ I (M3). このモデルでは、周期-振幅、周期-カラー関係は星団間で変わるが カラー・振幅関係は変わらない。 実斜線は与えられた M に対し、 P = 一定。 縦線=不安定帯の青縁と赤縁。 脈動定数 Q Q = Pρ1/2 = P M1/2/R3/2) = P M1/2Te3/L3/4 なので、 log P = log Q + 0.75 log L - 0.5 log M - 3 log Te (4) 詳細な研究結果は Q(M,L,Y,Z) を考慮して、係数がやや変わり、例えば Albada, Baker 1971 では、 logP = 11.497 - 0.68logM + 0.84 logL - 3,48logTe (5) 上式を見ると、 一定の Te に対し、ΔlogP = 0.055 を起こすには、 不安定帯での質量または光度に差がある必要がある。まず、M 15 と M 3 の 変光星質量は等しいと仮定しよう。すると、式(5)から ΔlogP = 0.84Δlog L だから、ΔMbol = -0.16 mag となる。 |
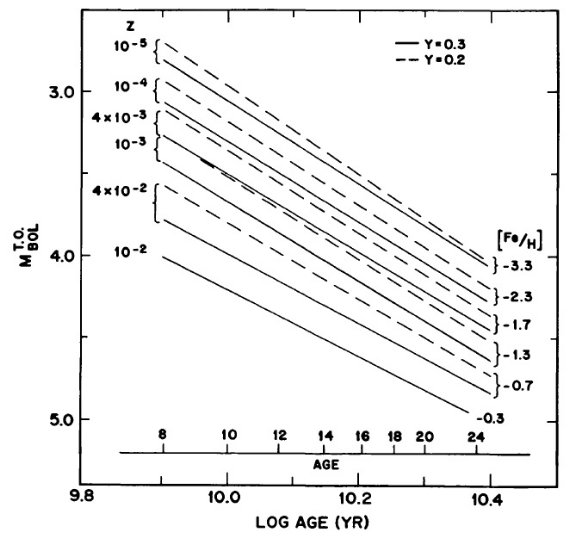 図14.年齢、ターンオフ等級、Y, Z の関係。 メタル量はシフトに関し逆に働く しかし、ZAHB モデルによると、与えられた Te に対する質量はメタル量に 依存する。 (∂logM/∂logZ)|logTe=3.85 = -0.066 (6) である。M 15 の方が M 3 より低メタルなので、M 15 ZAHB の質量の方が大き い。係数は log Te によって激しく変わる。例えば、 log Te = 4.1 (Y=0.3) の時,傾きは僅か -0.02 である。RR Lyr ではこの値より小さいだろう。しかし、 その正負のサインが本当であると認めると、同じ Te を持つ変光星を較べた時、 光度 L が同じなら、M 15 の方が M3 より周期が短くなくてはならない。観測 は逆であるから、L には先に計算したよりさらに大きい変化が必要とされる。 メタル量に起因する質量差の導入 式(6) を式(5) に代入する、つまり星団は同年齢だがメタル量の差によって、 RR Lyr 質量が変わると、考えると、等温度の星団変光星同士で、 ΔlogP = 0.045ΔlogZ + 0.84ΔlogL (7) [Fe/H]M15 = -2.15, [Fe/H]M3 = -1.69 とすると、 ΔZ = -0.46 となる。式 7 で ΔZ = -0.46、Δlog P = 0.055 から、 ΔlogLRR(M15-M3) = 0.090、つまり M15 HB は M3 HB より 0.22 mag 明るい。 他の機構がない 強調したいのは、光度シフト以外に周期シフトに対し満足な説明を与える説 明はないということだ。不安定帯のカラー境界が変動することは問題ではない、 と言うのは、各 Te 毎での周期の比を問題としているからだ。Stobie 1971 に よる複数回の不安定帯横断の問題も回避可能である。ヘリウムの問題は略す。 |