Tracing the Galactic Anticenter Stellar Stream with 2MASS M Giants

　アブストラクト

　1.イントロ　

　２．　データ選択と密度関数　

近赤外二色図（右図参照、 Bessell/Brett 88 ）は M-型の矮星と巨星をすぐに分離する手段を 与えてくれる。 我々は Majewski et al 2003 と同じく 2MASS データセット二色図上 で M-型巨星を選ぶが、彼らよりカラー巾を広げ、0.86 < J-Ks < 1.10 を加えた。これにより |b| > 34° の 4° × 4° の個々のフィールドでも十分な数のサンプルを得ることができるようになった。 我々は 51 ms 2MASS 露出データを排除した。その結果、我々のカタログでは Ks ≥ 8 mag の等級限界を与えられた。サンプル数は |b| = 34° で　14 - 27, |b| = 14° で 51 - 395 であった。目標が一角獣座システムの存在を確認し、 その長さと方向を決めることなので、解析は減光が穏やか、E(B-V) < 0.555, でバルジ星の混入が最小に抑えられる箇所に限定した。こうして、 |b| < 12 ° でかつ -54° < l < +54° の領域は除いた。 　個々の M-型星の [Fe/H] は判らないので絶対等級も不明である。単一メタル量 を仮定し、相対距離を確かにするのなら、カラー範囲を狭くして距離指数の分散 を小さくするという手段がある。しかし、そうするとサンプル数が減って広い グリッドが必要となり、その結果空間分解能が低下する。 　その代わりここでは個々の恒星に確率距離分布関数を与える。 P([Fe/H]) = メタル量確率分布関数。 P(D|Ks,J-Ks) = (Ks, J-Ks) の星が距離 D である確率密度。 以後、P(D|Ks,J-Ks) は P(D) と略す。 すると、 P(D|Ks,J-Ks) = P([Fe/H]) | d[Fe/H] | | dMKs | dMKs dD ここは良く分からない。表記を簡単にするため、M = 絶対等級、K = 見かけ等級、C = カラー、Z = メタル量、 D = 距離、とする。 　　　dN = F(K, C, D)dKdCdD = G(M, Z, D)dMdZdD とした時、 　　∂(K,C,D)/∂(M,Z,D) = (∂C/∂Z)M,D なので、 　 G(M, Z, D) = F(K, C, D)*(∂C/∂Z)M,D である。逆に 　 F(K, C, D) = G(M, Z, D)*(∂Z/∂K)C,D 上の P(D|Ks,J-Ks) は規格化定数を別として、F(K, C, D) のことらしい。すると、 P(Z) | dZ | | dM | = G(M,Z,D) ∂Z | dM dD ∂K C,D これは理解し難い等式である。そんな事を考えずに、 P([Fe/H])と Z に依存 する CMR,　つまり色メタル量等級関係を使って、 個々の星、つまり個々の (Ks, J-Ks) に対して、距離分布を与え、それらの総計 としてサンプル全体の距離分布を決めればいいのではないか？ 　簡単のため P([Fe/H]) はピークが一つの関数と考える。また、K-, M-巨星 に対してはメタル量に依存するカラー等級関係(Ivanov,Borrissova 2002) を 採用した。 （矮星を考えているのではない！） P([Fe/H]) は 中心値 μ = -1, 分散 σ = 0.4 のガウシャン を仮定した。 　P(D|Ks,J-Ks) の計算は次のように行った： まず、与えられた (Ks, J-Ks) に対して、[Fe/H] は一つの D に対応する。それを 上式の右辺に入れる [Fe/H] に使う。これは Ivanov/Borrissova 2002 の [Fe/H](MKs) を使うことでなされる。右辺の微分はこれらの式を 使って計算される。こうして決めた個々の星の距離確率分布関数を全ての星で 足して視線方向の密度分布が決まる。 （やはり、なぜ直接分布関数に行かないか判らない。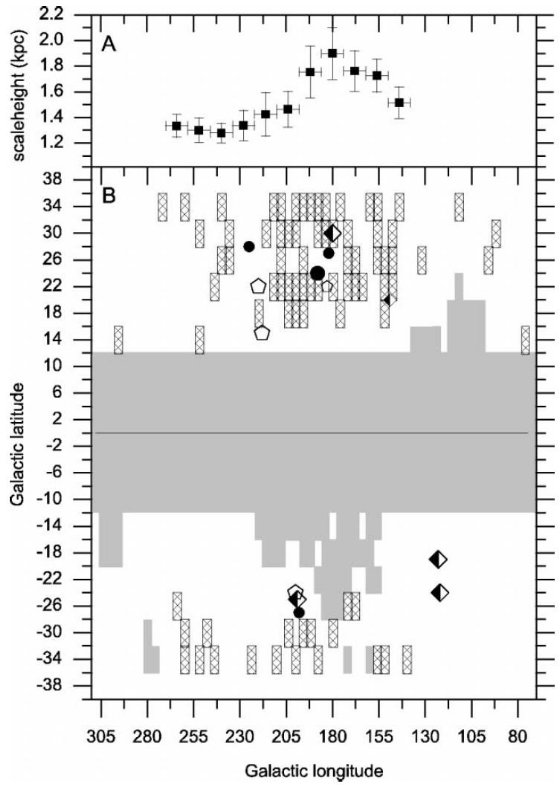） 　図１には距離分布関数の一般的傾向、円盤に対応する幅広の盛り上がりが手前 5 - 7.5 kpc に来て、ある方向ではさらに遠く 9 - 13 kpc の間に第２のピーク、 が示されている。別の方向では手前のピークがより広がり岩棚のようになる。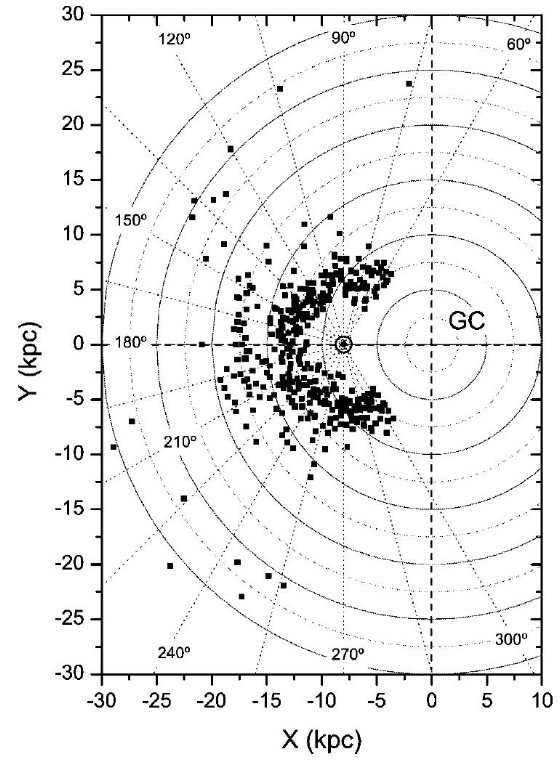 　図２にはピーク検出のまとめが示されている。大きくて近い方のピークは円盤 M 型巨星から来ている。これは我々のサンプルでは 4 kpc から始まる。図２の 外側のピークは太陽から 11 kpc 離れている。この帯は図 2a ではっきり見える。 これは距離確率分布関数の -36°: < b < +36° の広い範囲で認められ る特徴に対応している。ただしこれは南側では赤化が強くなるためはっきりしない。

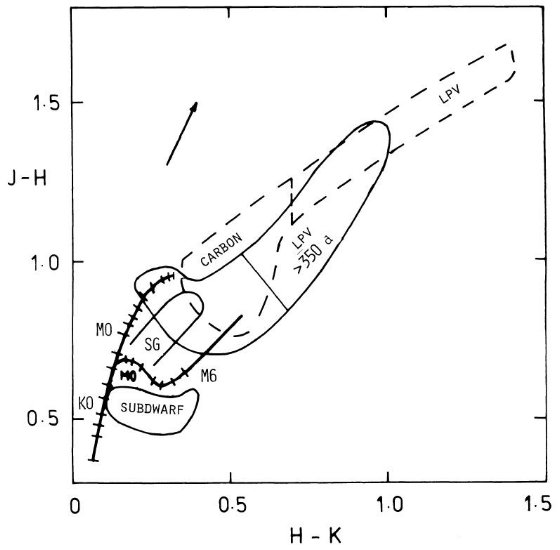
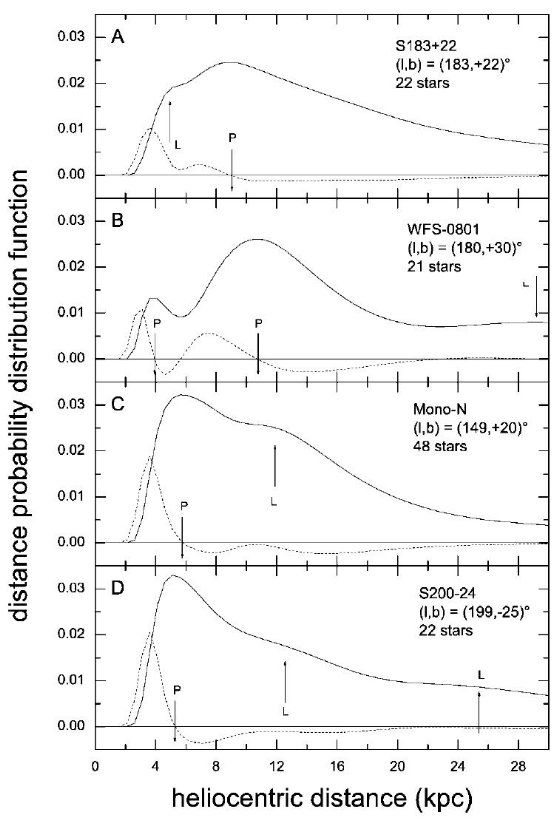
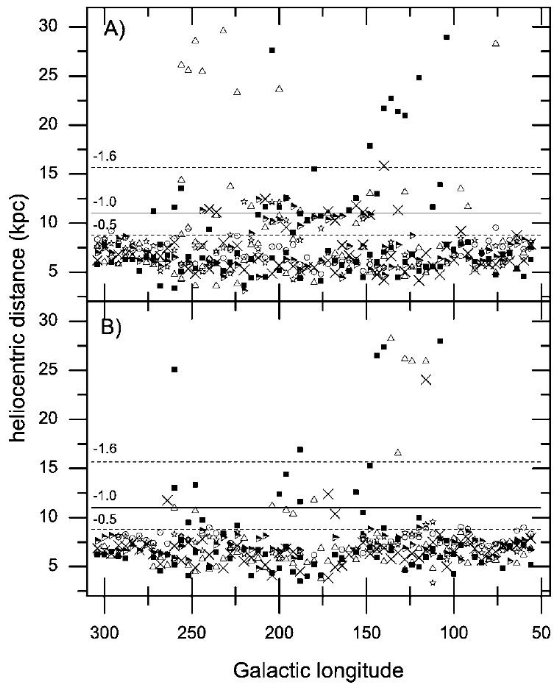
図 G5 - M6 の矮星と巨星の二色図。矢印は赤化。Bessell/Brett 1988. 図１．一角獣座構造が Ibata et al 2003 と Yanny et al 2003 で報告された ４領域における距離確率分布関数上のピークと棚。P (ピーク）がわれわれの 一角獣座構造の確認ということになる。 図２．縦軸＝ピーク位置の太陽からの距離。黒四角＝ 36° - 32°, 白三角＝ 32° - 28°, クロス＝ 28° - 24°, 右向き三角＝ 24° - 20°, 白星＝ 20° - 16°, 白丸＝ 16° - 12°。実線と破線は特徴の平均距離を平均 [Fe/H] = -1.6, -1.0, -0.5 に対して求めた。（-1 のガウシャンじゃなかったのか？） (a) 北銀河半球 (b) 南銀河半球。

　３．　一角獣座ストリーム　

図２の第２帯を一角獣座ハローストリームと考える。これは Ibata et al 2003 が オリオンリングと呼んでいるものと同じである。図２(a) では 150° l < 220 ° でこの特徴がはっきりしている。この領域では集められた M-巨星のうち 20 - 30 % が 9 - 13 kpc に集中しているようである。銀河面近くでは構造は 円盤巨星の数が増えるため、ピークから棚状になる。 　北銀河半球ではこの構造までの太陽距離は 11.2 ±0.11 kpc で、Newberg et al 2002, Yanny et al 2003, Ibata et al 2003 の 8 - 11 kpc と一致する。 図４には銀河面上に投影したが構造がはっきり見える。一角獣座構造は銀河中心 から 17.5 ±0.5 kpc 離れている。図４を良く見ると、第３象限では距離が 第２象限より小さくなっている。 　テストを繰り返した結果、（略） 　第１章では赤い 2MASS 星を使った以前の研究結果について述べた。その時の構造 は半分離型の中心が (-20, -7) kpc の斑点として見えた。Majewski et al 2003. この仕事は Sagittarius 中心核のカラー等級関係を用いている。この銀河は [Fe/H] < -1 と考えられている。この方法では各星に一つの距離が与えられる。 一角獣座構造がこのように赤い星でも見出されたというのは Yanny et al 2003 が 想定した [Fe/H] = -1.6 よりかなり高メタルの星が存在することを示している。 彼らの言うような低メタル星では would have few tip giants だろうからである。 （この論理はよく理解できない。） 図３．(a) スケール高の変化。(b) 文献にあらわれた特徴。灰色領域は減光が強い所。 バツ四角＝ 9 - 13 kpc ピークが見つかった。五角形＝ Newberg et al 2002, 丸＝ Yanny et al 2003, 半黒菱形＝ Ibata et al 2003

太陽距離 9 - 13 kpc, 140° < l < 270° の星は全て一角獣座 構造のメンバーと仮定して、スケール高を 1.3 ± 0.4 kpc と見積もった。 これは Yanny et al 2003 の 1.6 kpc と合う。Ibata et al 2003 は半分くらい の厚みを出しているが、彼らの距離は 8 kpc と近いのでそれも薄さの一因で あろう。 　図４は構造が l = 270° 付近で銀河系円盤に溶け込んでいくことを示す。 一方、反対側でも l < 90° では構造が消滅しているようだ。 -90° < l < 90° では 2MASS は内側銀河の巨星を多く拾って いて、消滅はそのためかも知れない。いずれにせよ（？）、本研究は 一角獣座構造は一様なリングではない。 　Helmi et al 2003 はマージャーの数値計算から同一面内の衛星銀河降着 が一過性の星の弧を作るというモデルを提示した。この説が観測に近く 思える。 図４．銀河面上への北銀河半球内ピーク位置投影。一角獣座構造は銀河系中心 から 16 - 17 kpc に見える狭い帯である。帯は 195° < l < 240° で厚く、l ≈ 270° で円盤に溶け込んでいる。