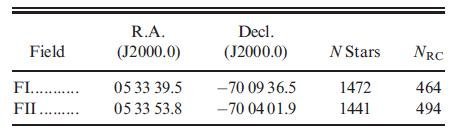
表1.観測領域の座標
アブストラクトレッドクランプによる LMC 距離LMC バーの2領域で NTT による J, K 撮像を行った。K, J-K 色等級図の分解能 は素晴らしく、数百のレッドクランプ星の存在を明らかにした。Alves による ヒッパルコスレッドクランプ星の K バンド絶対等級の較正値を用いて、我々は 観測領域までの距離指標を 18.487 と定めた。 エラー評価 この結果のランダムエラーは ±0.008 で、系統エラーに測光ゼロ点、 ヒッパルコス較正のエラー、赤化不定性を考えると ±0.048 になる。 バーの傾きと種族効果 バーの傾きを Marel et al の 幾何学モデルから採用して補正すると、LMC 重心までの距離は 18.501 となる。 Alves et al の種族効果を考慮すると、18.471 になる。これはAlves et al、 Sarajedini et al の求めた値とよく一致する。しかし、強調したいのは 現在のところ種族効果の補正エラーは 0.12 等に上る。この値を下げることが 大事である。 レッドクランプ星のJ等級 レッドクランプ星のJ等級も決めた。もし J 等級の種族効果が K 等級よりも 小さいことが将来判明した場合には有用な結果である。 |
1.イントロこの論文では RC で LMC 距離を求める。ARAUCARIA 計画では距離指標、セファイド、RR Lyr, レッドクランプへのメタル、 年齢効果に特に注意を払っている。ここでは、LMC への距離をレッドクランプ から求める。 レッドクランプの距離指標への利用 レッドクランプを距離指標へと利用した初めは Paczynski, Stanek 1998 で、 レッドクランプの平均 V, I 等級が較正された。重要な進歩は Alves 2000 が 多数のヒッパルコスレッドクランプ星のK等級を較正したことである。I 等級には 減光の補正と僅かではあるがメタル量依存性の問題があり、それはレッドクランプ I 等級を使った LMC 距離、 Udalski et al 1998, 2000, Romaniello et al 2000、 の不一致に現れている。K 等級の利用はこの問題を軽減させる。Grocholski, Sarajedini 2002 では、散開星団の 2MASS データを使って K 等級の種族効果が 研究された。その結果、MI よりも MK の方が年齢、メタル 効果が小さいことが示唆された。したがって、 MK の種族効果を詳細に 調べることはレッドクランプにより距離を正確に見積もる上で極めて重要である。 近赤外データ この論文では、 LMC バー内の2領域でこれまでになく高精度と我々が信じる 近赤外データを提示する。これらは NTT で素晴らしいシーイングの下で撮られた。 このデータに OGLEII の可視域データを合わせ LMC 距離を求める。 |
| NTT;SOFI 広視野モード(2'.49 × 2'.49, 0".146/pixel) で 撮ったデータは PSF も均一で高い測光精度に役だった。2領域が K, J バンドで撮られた。シーイングは 0".6 であった。スカイ条件の 変動が速いので Ks バンドでは 10 秒積分を 6 回続けて行い、それから 望遠鏡を 20" 動かした。これを 20 回繰り返した。これは、ネットの積分時間と しては 20 分間に相当する。J バンドでは各地点で 10 秒積分を 1 回行うだけで ネット積分時間は 3 分である。標準システムに変換するため 7 個のUKIRT 標準星 (Hawarden et al 2001) を各 9 回観測した。 |
 表1.観測領域の座標 |
|
アパーチャ補正 データ整約は IRAF で行われた。PSF モデルを求める方法は Pietrzynski. Gieren, Udalski 2002 に述べた。アパーチャ補正を導くため各画像中に約 50 の孤立星が 選ばれ、周囲の星を逐次的に差し引いた後にそれらの星のアパーチャ測光を行った。 それらの星のアパーチャ補正値のメディアンを画像毎の最終補正値として採用した。 こうして決めた補正値の rms 分散は 0.008 等である。 システム変換 標準星のアパーチャ測光は 14 ピクセルアパーチャで行われた。装置等級は 以下の式で標準システムに変換された。 J - K = 0.939(j - k) + 0.620 K = k - 0.036(j - k) - 2.704 ここに、 J - K と K は UKIRT システム、j - k と k は 1 秒積分に対応する アパーチャ装置等級とカラーを示す。 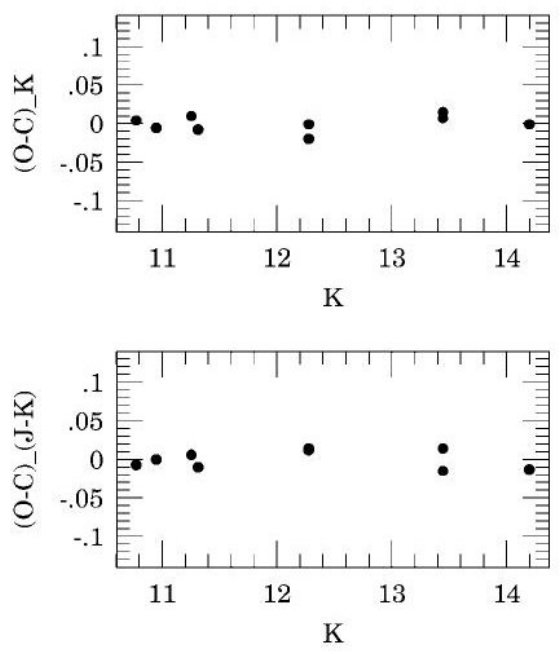 図1a. 標準星の (観測ー計算)K と (観測ー計算)J-K 対 K 等級 |
変換エラー 上式のように、カラー係数はそれぞれで 1 と 0 に近く、我々の装置が UKIRT システムに近いことを示している。図1が示すように、残差は 0.02 等以下で、 等級やカラーに依存していない。J, K 等級のゼロ点の総エラーは 0.03 等以下と 見積もられる。 測光ゼロ点の精度をテストする 測光ゼロ点の精度を外部データを使って調べるため、2MASS の中から測光精度が 十分に高く、我々のデータと共通する星を探した。その結果。19 の星が見つかった。 結果を比較する前に我々の値を 2MASS システムに変換しなければならない。そうして 比べた結果、我々の測光値と 2MASS 等級との差は K 等級で -0.01 ± 0.04, J - K で 0.00 ± 0.05 であった。 もう一つ独立なテストとして、我々の出したレッドクランプ平均 K 等級を Alves et al 2002 のと比べた。 Alves et al 2002 は ⟨K⟩Koornneef = 16.974, 一方我々は ⟨K⟩UKIRT = 16.895 を得た。両方を 2MASS システムに変換し、van der Marel et al 2002 の円盤傾き角を採用して我々 の領域が Alves et al より 0.025 等近いことを補正すると、我々の平均等級が Alves et al より 0.001 等明るいことが判った。この素晴らしい一致と、Sarajedini et al 2002 ともよく合っていることを見ると測光ゼロ点に関する系統エラーは非常に 小さいと看做せる。 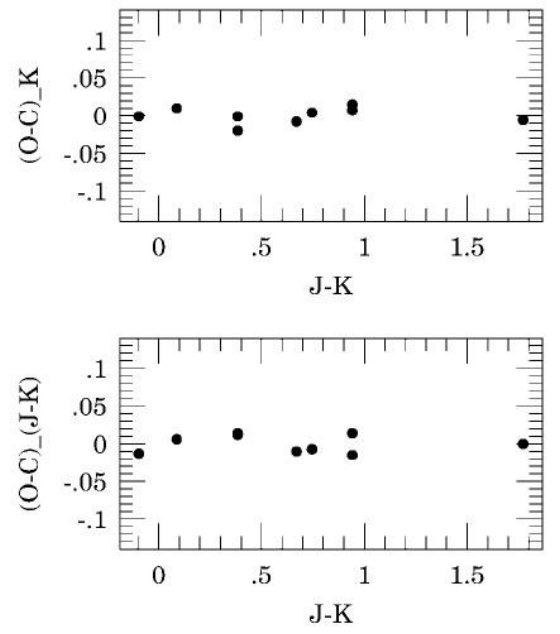 図1b.標準星の (観測ー計算)K と (観測ー計算)J-K 対 J-K カラー |
|
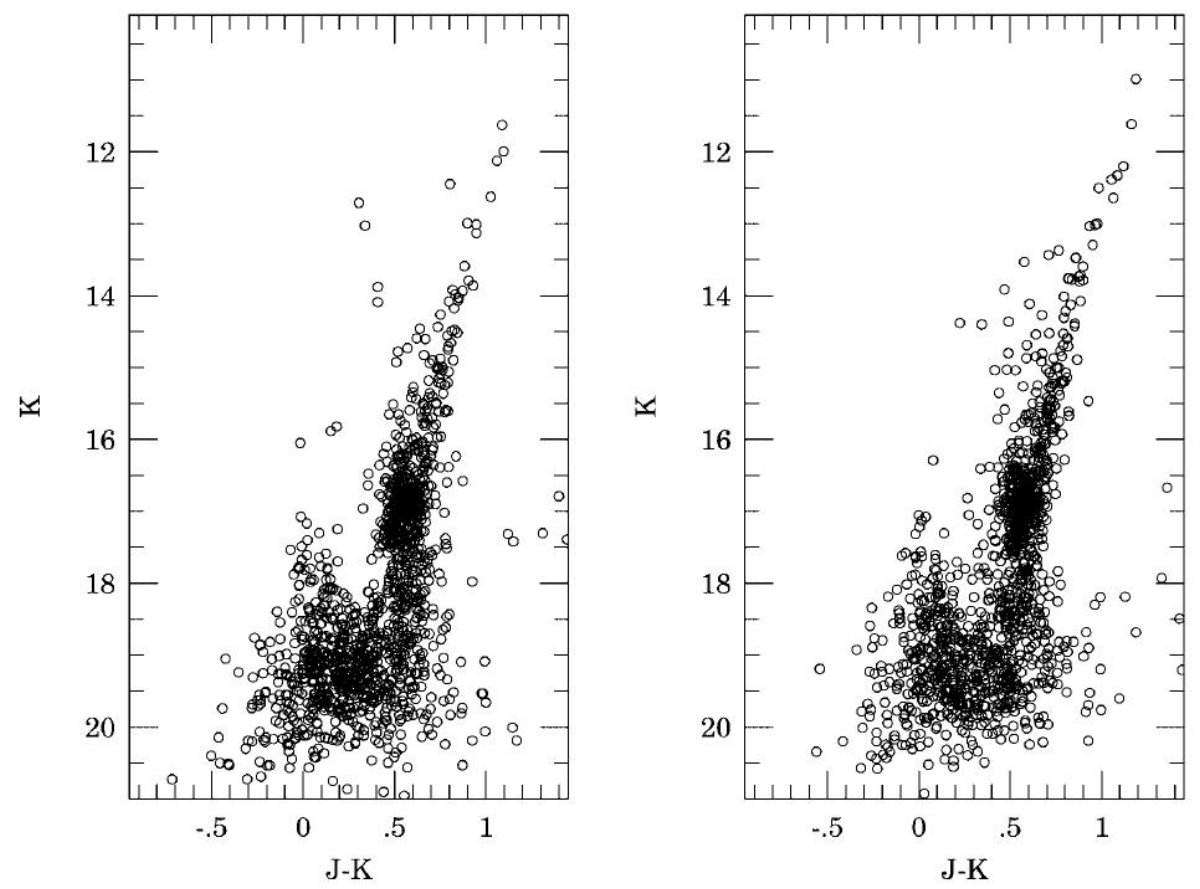
CMDに見えるもの 図2には2領域での K, J-K CMD (UKIRT システム) を示す。K 測光が 20.5 等に 達していることが見て取れる。双方でレッドクランプははっきり現れている。 この図は LMC でこれまでになされた最も深い測光である。図には主系列と赤色巨星枝 もはっきり見えている。それらは別途論じる。 等級分布のフィット レッドクランプ星の平均 K 等級を導くため、J-K = 0.35 - 0.80, K = 16 - 18 を 選んだ。K 等級を 0.05 等の区間に分け、Paczynski, Stanel 1998 に倣い、次の式 にフィットした。 n(K) = a + b(K-Kmax) + c(K-Kmax)2
J, K 平均等級 求めた結果が区分け巾の影響をどのくらい受けるかを見るため、等級 0.3、カラー 0.1 の計算も行ったが結果は同じだった。フィールド I では K 平均 = 16.893 ± 0.012, フィールド II では K 平均 = 16.898 ± 0.010 であった。 J 平均はフィールド I で 17.498 ± 0.012, フィールド II で 17.512 ± 0.011 であった。 両フィールドの値は良く一致している。これは間隔が 20' しか離れていず、 LMC バーの傾きによる距離のずれが小さいことと一致する。そこで、二つを合体 した。図3はその CMD 、下の図4はそれへのフィットである。得られた値は J = 17.507 ± 0.009, K = 16.895 ± 0.007 であった。 |
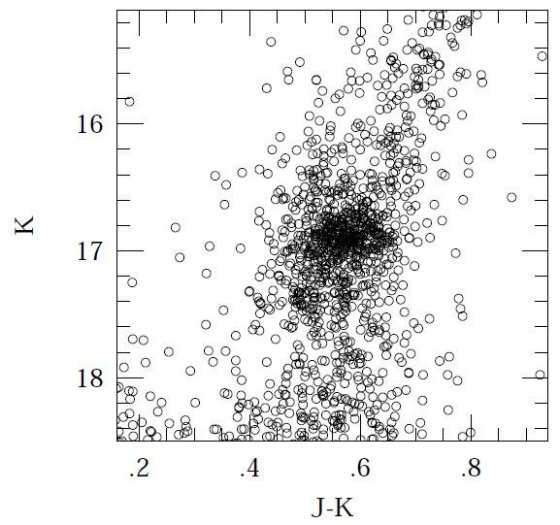 図3.合体後の色等級図。 |
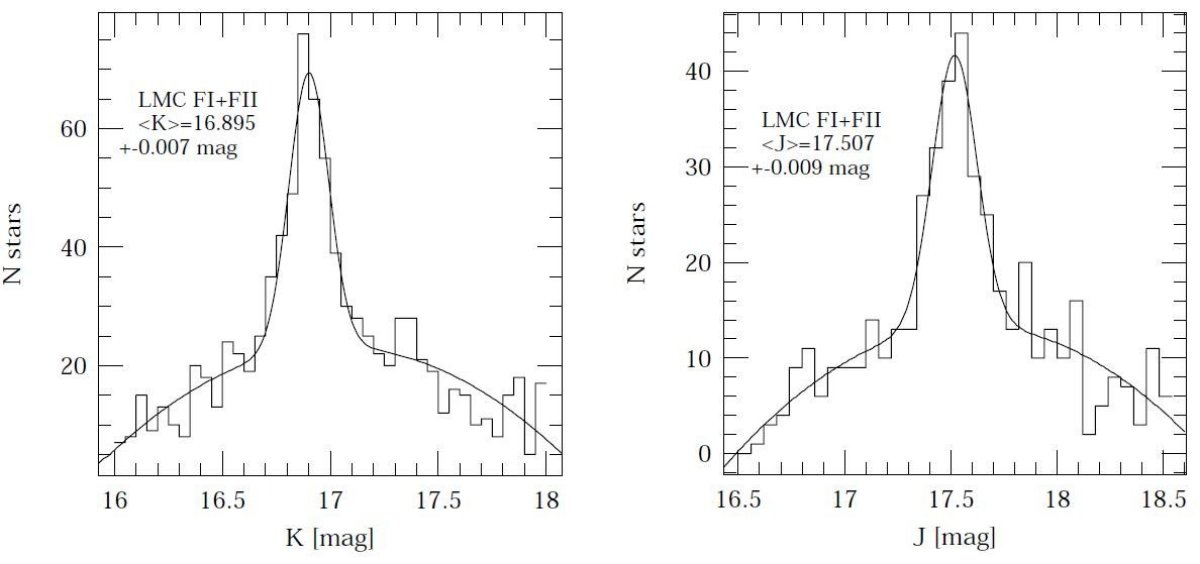
|
減光の評価 Udalski 1999 の OGLE II 減光マップから観測領域では E(B-V) = 0.152 を採用した。 (しかし、この減光マップはバーの傾きを考慮していないし、 種族効果も入っていない) この減光マップはレッドクランプ平均等級を 減光の指標にして作られ、ゼロ点は OB 星 (Udalski et al 1998, Lee 1995) や RR Lyr (Walker 1993) からの3箇所での減光測定で決めた。Udalski et al 1999 が 述べているようにこの 3 箇所の減光量は (2/1000) 等の精度で一致 している。さらに、LMC 周辺部の星団内と星団外のレッドクランプ星の減光フリー パラメターと I 等級を比較して減光の絶対較正を行った結果 (Udalski et al 1998) も 0.01 等以下のよい一致を与えている。こうして、我々は減光エラーは 0.02 等 以下と考える。Harris, Zaritsky, Thompson 1997 による研究では赤化のエラーは もう少し大きく 0.035 等くらいである。しかしその程度の違いは結果に影響しない。 K 減光量 Schlegel, Finkbeiner, Davis 1998 の 標準減光曲線、すなわち UKIRT システムの AK = 0.376 E(B-V), AJ = 0.902 E(B-V) を用い、 AK = 0.055, | AJ = 0.137 である。その補正を加え、 ⟨K⟩0 =16.839, ⟨J⟩0 = 17.370 を得る。 これは LMC レッドクランプの J 等級の最初の決定である。 LMC までの距離 ここで求めた ⟨K⟩0 をヒッパルコスレッドクランプ星の K 等級 (Alves 2000) と比べるため、Carpenter 2001 の与えた Koornneef 1983, 2MASS, UKIRT システムの変換式を用いる。注意すると、UKIRT と 2MASS の K 等級 間の差は (Ks)2MASS = KUKIRT + 0.004 (J-K)UKIRT + 0.002 からレッドクランプで 0.004 等で小さい。ヒッパルコスサンプル(Kooeneef ?) から UKIRT システムへ移る補正は 0.044 等である。この補正を加え、種族効果を 無視すると、LMC への距離指標 = 18.487 ±0.008(ランダム) ±0.045(系統) である。系統誤差はヒッパルコスで決めたレッドクランプ絶対等級の誤差 0.03 等、 我々の使用している測光ゼロ点の誤差 0.03 等、システム変換誤差 0.01 等、赤化の 誤差 0.02 等である。van der Marel et al 2002 の幾何学モデルを採用すると LMC 重心までの距離指標は 18.501 ±0.008(ランダム) ±0.045(系統) である。 |
|
種族効果 Girardi et al 1998, Girardi,Salaris 2001 は色々な環境下でのレッドクランプ 絶対等級の種族効果を調べた。特に、太陽近傍と LMC での星形成史と化学進化を 仮定した下で Girardi,Salaris 2001 は種族合成モデルから、LMC レッドクランプ星 で LMC 距離を求める場合には ヒッパルコスサンプルには K, I, V で -0.03, 0.2, 0.3 等を加えて、メタル量と年齢の補正をすべきであるとした。この -0.03 等 は Alves 2002 が種族効果を考慮する際に採用された。同じ補正を行うと 我々の LMC 重心までの距離指標は 18.471 となり彼らと素晴らしい一致を示す。 |
種族効果の誤差を小さくしなければ 不幸にも、 Girardi,Salaris 2001 にはこの補正のエラーが示されていない。 これら補正値の不確定性を評価するには全く異なる星形成史と化学進化に基づく 種族合成モデルの計算が必要である。さらに進化モデルのエラーも考えるとこの 論文の範囲を超える。あまり大きな違いはないモデルでだが、 Girardi et al 1998 と Girardi,Salaris 2001 の計算を見ると I で 0.115 等の差がある。K 等級に関しては モデル例が無いが同じくらいのエラーがあると考えてよい。したがって、 この種族効果の誤差を出来る限り小さくすることが極めて重要である。 Udalski 1998, 2000 では I 等級の種族効果に 0.04 等しか取っていない。これは星団レッドクランプ 星の研究から得られた値だが、モデルからの 0.2 等 とは大きく異なる。これは モデルと観測の双方でさらに研究する必要のあることを意味する。 |