The Distribution of Galactic Disk Stars in Baade's Window

　２．データ　

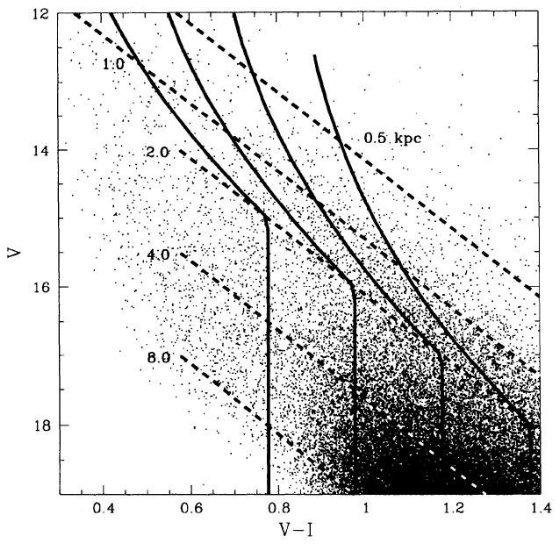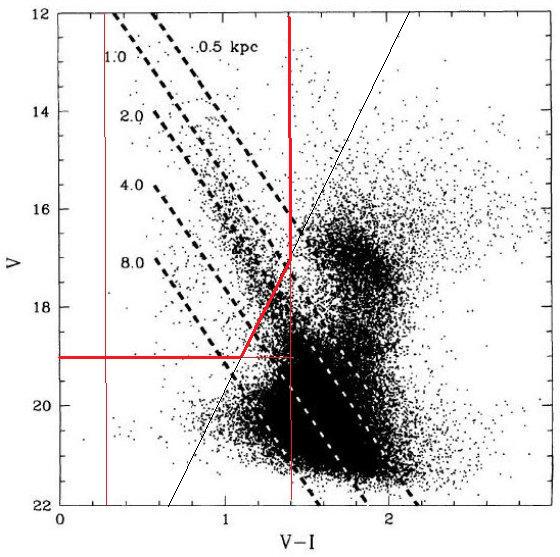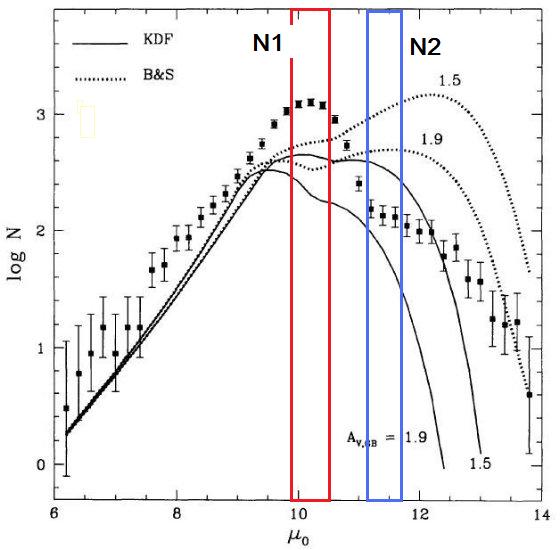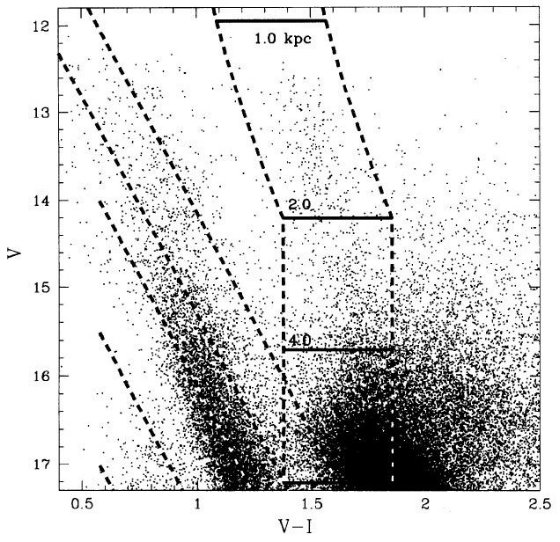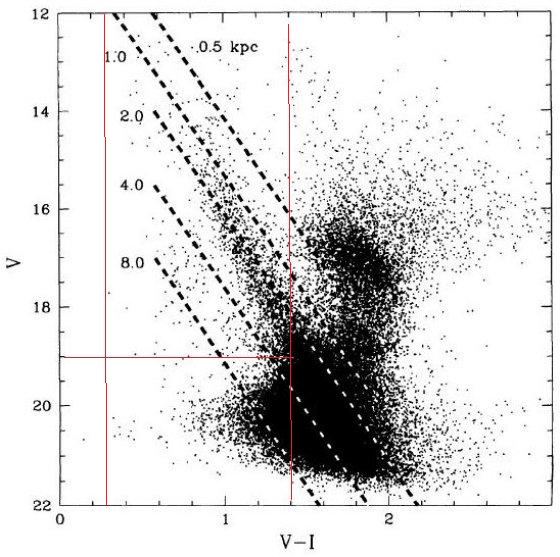
図１．BW OGLE 9 領域中心部の V - I 色等級図。５本の破線はプレアデス 主系列を 0.5, 1, 2, 4, 8 kpc においたもの。星間減光は Arp 1965 を 使用。図中の大部分はバルジだが、2 kpc に集中した主系列が見える。 ＢＷの色等級図　 　Udalski et al 1993a はバルジの 14 領域、6 × 105 星の色 等級図を提示した。観測は 1 m Swope 望遠鏡 + 2kx2k Ford/Loral CCD を用いて 行った。ここではＢＷ９領域のデータを調べる。図１にその中央領域(BWC)の 色等級図を示す。５本の破線はプレアデス主系列を 0.5, 1, 2, 4, 8 kpc においた ものである。星間減光は Arp 1965 cf. Eqa (3), AV, GC = 1.5 を 使用した。図中の大部分はバルジだが、2 kpc に集中した円盤主系列が見える。円盤 星が集まっている部分を 9 領域全部の星を集めたのが拡大図が図２である。 ４本の実線は４つの円盤星、[Mv,(V-I)o] = [1.0, 0.0], [3.0, 0.2], [5.0, 0.4], [7.0, 0.6] の距離による変化を示す。図２には 16,000 個の星が含まれるが、その殆ど 星が円盤上にあると我々は信じている。

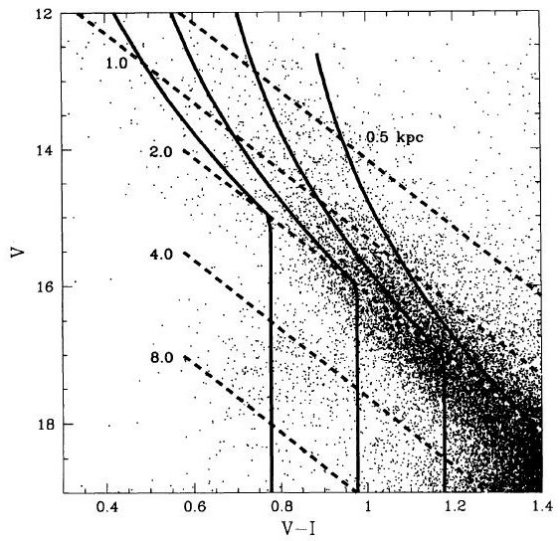
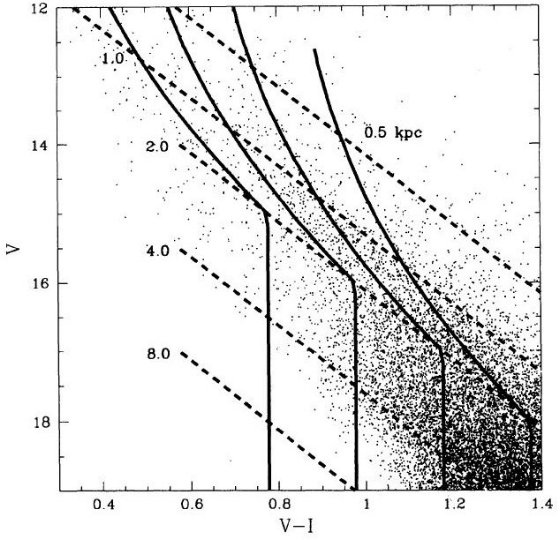
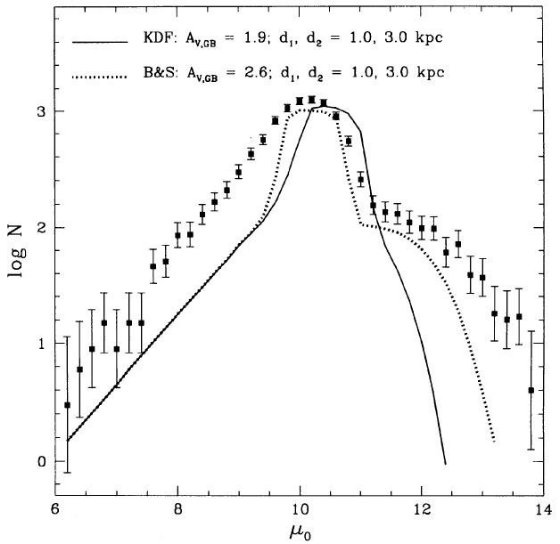
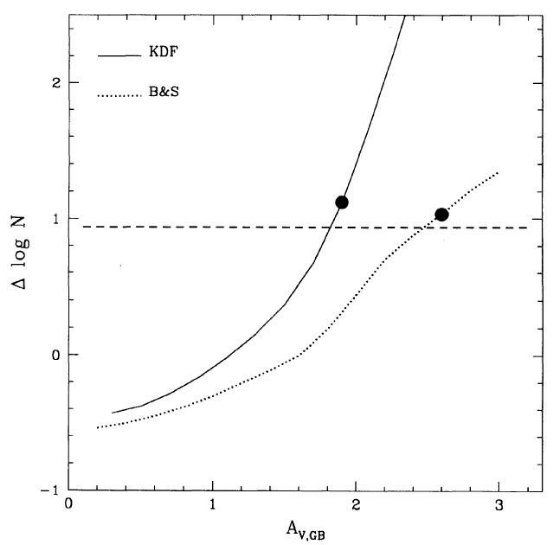
図２．BW OGLE 9 領域全ての V - I 色等級図。破線の意味は同じ。４本の 実線は４つの円盤星、[Mv,(V-I)o] = [1.0, 0.0], [3.0, 0.2], [5.0, 0.4], [7.0, 0.6] の距離による変化。殆ど全ての星が円盤上にあり、 90 % の星が 3 kpc より近い。 　円盤密度分布とＢＷ方向のスターカウント　 　標準的 B&S モデルでは円盤の数密度は高さ方向にはスケール高 300 pc の指数型、 動径方向ではスケール長 3.5 kpc の指数型となる。この二つの効果が一緒になり、 バーデ窓方向を見ると、 数密度は距離に対してほぼ一定となるはずである。 その場合、星間減光を無視すると、同じカラー（同種の星）での等級分布は一等毎に ４倍 (&sim: 100.6Δm)になるはずである。これが太陽からの距離 2 kpc 以内で観察されることである。 　2 kpc より先の劇的な密度低下　 　しかし、 2 kpc より先では劇的な密度低下が現れる。BW 以外でもこの現象は観察されて おり、 　　　　　Rodgers et al 1986 (l, b) ≈ (0°, -25°), 　　　　　Turndrup 1988 (l, b) ≈ (0°, -8°), 　　　　　Tyson 1991 (l, b) ≈ (1°, -2°), 　　　　　Ortolani et al 1992 (l, b) ≈ (14°, -1°), が挙げられる。我々のデータが最もはっきりしている。

中心領域 BWC の減光　 　ＢＷ方向の星間減光は議論の価値がある。NGC 6522 方向には、 Arp 1965, Walker, Mack 1986, Terdrup 1988, Walker,Terndrup 1991 などの研究がある。それらは Av = 1.5 から Av = 1.78 に渡っている。我々はもっともらしい値として、まず AV, BWC = 1.5 （Arp 1965, Terndrup 1988）を採用する。他の Av の場合は第４章で論ずる。他領域の減光は次のように決めた。 　減光フリーパラメター による RGB 星と RC 星の選択　 赤色巨星を次の条件で選んだ。 　　　1.5 < V-I < 2.4, 13.0 < VV-I ≡ V-2.6(V-I) < 14.5 レッドクランプ星は次の条件で選んだ。 　　　1.5 < V-I < 2.4, 11.5 < VV-I ≡ V-2.6(V-I) < 13.0 どの領域にも赤色巨星 3000 個、レッドクランプ星 4000 個が見つかった。 パラメター VV-I は減光フリー等級である。 　カラー分布シフトから減光を決める 　 (V-I) カラー分布を各グループ毎に全ての領域で求めた。分布の形は互いに類似 しているが、減光量が異なるので (V-I) カラー方向にシフトしている。それを 表１に示す。第４，５列は領域と中心領域 BWC とのカラーシフト量 Δ(V-I) である。第６列は各領域に適用した減光量 AV,GB である。 最後の列にはレッドクランプ星の VV-I 分布がピークになるところの値を示す。 　rms 差 = 0.03 で二つの決め方のカラーシフトはよく一致している。９領域の 平均減光量は NGC 6522 方向より Av で 0.09 mag 大きい。 　表１によると、 VV-I 分布のピークは 12.36±0.03 にある。全領域でそうであるのはこの量が星間減光の影響を消していることを 示唆している。

表１．赤色巨星とレッドクランプカラーシフトから決めたＢＷ９領域の減光 ただし、 VV-I と AV,GB との間には いくらかの相関が見られ、これは採用した AV/EV-I = 2.6 が不正確であることを示唆している。 　Av の距離依存性　 Arp 1965 に従って、次の式を採用した。 　　　　　 AV(d) = AV,GB × (d/2kpc) 　　　 for d < 2 kpc 　　　　　 AV(d) = AV,GB 　　　　　 　　　 for d > 2 kpc

　３．標準モデル　

図３．モンテカルロで作った銀河系円盤の色等級図。図１と同様に５本の破線は 距離 0.5, 1, 2, 4, 8 kpc においたプレアディス主系列に Arp 1965 の減光 を加えたラインを示す。４本の実線は円盤主系列上の点 [Mv, (V-I)o] = (1.0, 0.0), (3.0, 0.2), (5.0, 0.4), (7.0, 0.6) を示す。このモデル図の星の大部分は 3 kpc 以遠であった。

図４．図３と同じだが、円盤スケール高を銀河中心に向かうに連れ減少させた。 （Kent et al 1991）

　比較のため図２と図３を再度掲載。まあ確かに。

図２.観測CMD

図３.モデルCMD

　４．議論　

スケール高を変化させたモデル　 　Kent et al 1991 は標準モデルの改訂を試みた。彼らは近赤外スケール高が 太陽付近 (RGC = Ro = 8 kpc) では 247 pc であるのに、銀河中心距離 RGC = 5 kpcでは 165 pc しかないことを見出した。我々はスケール高を H(Mv, RGC) = H(Mv, Ro) × ( 1 - 0.89 RGC ) Ro と単純に線形に変化させた。 ( 上の RGC は Ro - RGC に置き換えるべき。) 他は同じで再計算した結果が図４である。依然観測と合わない。 　距離指標 μ と仮指標 μ0 　距離指標は以下の式で定義される。 　　　　　μ ≡ 5 log(d/10 pc) = V - 5(V-I) - 1.0 + [5 EV-I (d) - Av(d)] ここに、5 EV-I は赤化の、Av は減光の補正である。これは直接には 測れない。どちらかと言えば適用するモデルで決まる。しかしながら、パラメター μ0 ≡ V - 5(V-I) - 1.0 は全ての星に対して計算できる。もし 減光が無ければ、 μ = μ0 となる。 　円盤星をバルジ星から分離する　 　円盤星をバルジ星から分離するため以下の領域を切り取った。 　　　　　　　V < 19.0,　　V - I < 1.4 　　　　　　　(V - I) + 0.15 (V - 19.0) < 1.1

図１改．太赤線が円盤星の領域。

モデルの仮指標 μ0 分布が観測と合わない　 次に上の領域内の星を Δμ = 0.2 の区間に放り込んだ。その結果 を次に議論する。図５の実線は 　 B&S 標準モデル で期待される分布、破線は Kent et al 1991 のスケール高変化モデルである。 どちらも Arp 1965 の減光を採用している。AV,GB = 1.5 のラインが 図３と図４に対応している。明らかにどのラインも観測に合わない。スケール高変化 モデルの方がやや近いが。 　μ0 = 10.7 での急落　 　観測の著しい特徴は μ0 = 10.7 での急落である。この落下量の指標として、 　　　　　　　Δlog N ≈ log N1 - log N2 をとる。ここに、 N1 = 9.9 ≤ μ0 ≤ 10.5 の星数、 N2 = 11.1 ≤ μ0 ≤ 11.7 の星数である。 図５．ＢＷ方向円盤星の仮指標 μ0 分布 N(μ0)。 エラーバーは N-1/2を示す。区間巾は 0.2 である。実線は B&S 標準モデル。

急落をモデルで再現する　 この大きな Δlog N ≈ を説明するために、減光分布を変えて試した。 　新しい減光モデルは 　　　　　　　 Av = 0　　　　　　　　　　　　　　　　　　for d < d1 Av = AV,GB × d - d1 　　　　　 for d1 < d < d2 d2 - d 　　　　　　　Av = AV,GB　　　　　　　　　　　　　　　 for d2 < d ここに、d1, d2, AV,GB は３つの調整パラメター である。 AV,GB 毎に、d1, d2 を動かして 　Δlog N の極大値を探した。その結果が図６である。観測値を再現するのは Kent et al モデルでは 　　( AV,GB, d1, d2) = (1.9 mag, 1 kpc, 3 kpc)、 標準モデルでは 　　　　　　( AV,GB, d1, d2) = (2.6 mag, 1 kpc, 3 kpc) であった。 図６．水平長破線は観測された Δlog N の値。実線は B&S 標準モデルに対する 極大 Δlog N, 単破線は Kent et al モデルのそれを示す。

図７．Δlog N の観測値を再現した時の μ0 分布。 実線は Kent et al モデル。点線は B&S モデル。 　観測とモデルの差　 　上で選ばれたパラメターに対する μ0 分布を図７に示す。 図を見ると分かるように、ドロップの値は再現しているが、観測と異なり μ0 = 9.5 付近の傾きが強過ぎる。 　観測された星の分布には二つの大きな特徴がある。 （１）0 < d < 2.5 kpc の星はモデル予想の倍くらいある。これは、 Rodgers et al 1986, Terndrup 1988 が既に気が付いていた。 （２）2.5 kpc を越すと星数が急落する。この距離はサジタリウス腕の 位置と一致する。 　腕に古い星が集中するのか？　 　腕に若い星が集中するのは自然である。しかし、図２で細い主系列を 形成している星の大部分は 4 < Mv < 7 である。これらの星の 主系列年齢は 10 Gyr に近いかそれを上回る。円盤内の星形成率が過去 108 - 109 yr で劇的に増加はしていないと考える のは自然であろうから、それらの星の大部分は古い星であろう。そうで ないと考える場合は d = 2 kpc では何十億年の間星形成が抑えられていた ことになり考えにくい。

図８．OGLE 観測の 9 領域色等級図。５本の破線は Arp 1965 星間減光に 対する d = 0.5, 1, 2, 4, 8 kpc のプレアディス主系列。４本の水平実線 は d = 1, 2, 4, 8 kpc のレッドクランプ。 　 腕に星が集中するわけ　 　腕に古い星が集中するのは驚くべきことだが他に例が無いわけではない。Rix, Rieke 1993 は M51 で類似の現象を近赤外表面測光から見出している。今回の発見は それが我々の銀河系でも起きていることを示唆している。我々は銀河系の二つの モデルを使ってこの現象を説明しようとした。しかし、サジタリウス腕に星が 集中しているという説明以上に上手い解釈は見つからなかった。Av ≈ 1.5 mag では 2.5 kpc 先の大きなドロップを説明できないことがわかった。Av ≈ 1.9 mag を仮定し、変化するスケール高モデルを採用すると、そのドロップを合わせることが 出来る。しかしそのモデルは同時に μ0 = 9.5 にも大きなジャンプ を産み出す。これは観測されていない。次に、スケール高一定モデルでは Av ≈ 2.6 mag と受け入れがたい大きな値を必要とする。また、μ0 = 9.7 に大きなジャンプが出来るのも問題である。 サジタリウス腕の向こう側で星がない　 　この時点では、サジタリウス腕の向こう側で円盤主系列星に劇的な減少 があると考えざるを得ない。