2.a. 観測
各領域に2種類の乾板が使われた。観測は AAT 3.9 m 望遠鏡を使って行われた。 まとめを表1に載せた。2.b. データ整約
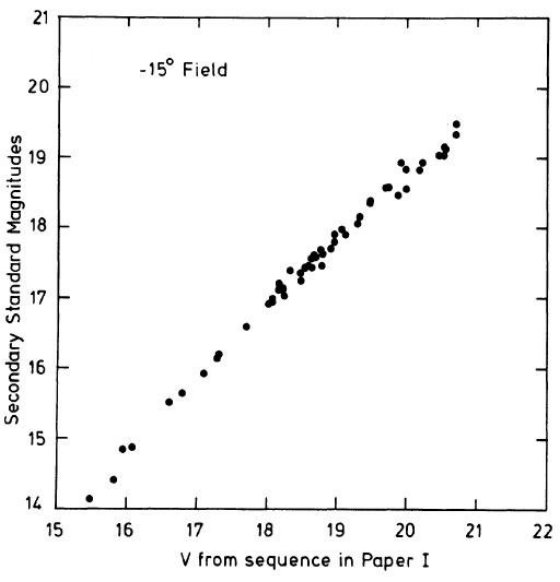
図1a.二次標準星の V バンド写真測光等級と光電測光の比較。
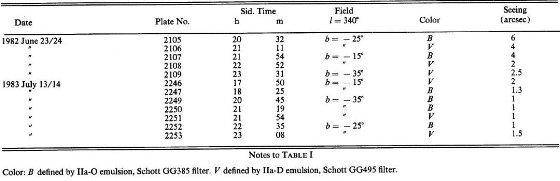
表1.観測のまとめ。
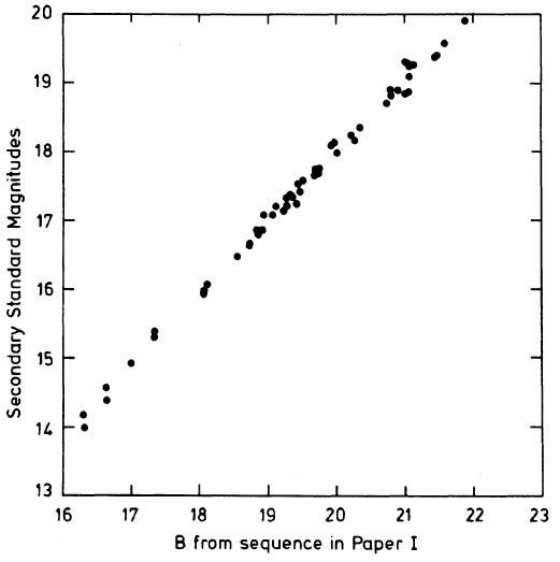
図1b.二次標準星の B バンド写真測光等級と光電測光の比較。
アブストラクトバルジの3領域でスターカウントを行ったバルジの3領域、l = 340°, b = -15°, -25°, -35° の V = 15.5 - 21.5 での見かけ微分光度関数(スターカウント)、カラー分布、色― 等級格子を提示する。各領域は 27 arcmin の大きさで、12万の星を含む。スター カウント色分布を B&S モデルと比較した。 太陽から 3 kpc に若い種族の超過が見られる スターカウントの予測との一致はまあ良いが、適用した楕円体成分の持つ球状星団 的な特徴は示さなかった。太陽から 3 kpc のあたりで円盤光度関数が van Rhijn- Wielen 関数と大きくずれる。太陽近傍での v = +4.5 の サルピータ不連続より明るい 所で超過を示している。この若い種族は古い円盤と同じスケール高 370 pc を持つ。 バルジ成分の性質 古いバルジ星へのターンオフフィットは銀河核への距離 8.4 kpc を与える。バルジ 星成分は銀河中心距離が小さくなると 47 Tuc タイプ星の割合が増加する勾配を 示す。 |
1.イントロBahcall, Soneira モデル最近の Bahcall, Soneira モデル (1984) には Burstein, Heiles 1982 の減光マップに合うようにダスト層が加えられた。彼らは銀極方向に気を配った がそこは楕円体成分の幾何学パラメターと共に、円盤成分/楕円成分の太陽付近 での規格化を調べるのに便利な領域である。色々な領域でのスターカウントとの 比較から、現在では円盤スケール長として 3.5 kpc, スケール高として 325 pc が 得られている。楕円体成分は有効半径 2,7 kpc、 扁平比 e = 0.8、太陽距離で 楕円体密度/円盤密度 = 0.2 % の規格値を有する。光度関数には Wielen dip が付いていて、銀河系全体で適用可能と仮定されている。 パラメターの一意性 インプットされる仮定は一意には決められない。例えば、種族成分の数も見かけ 光度関数とカラー分布からでは制限が付けられない。この点は最近の「厚い円盤」 を廻る Bahcall, Soneira 1985 と Gilmore et al 1985 の論争にも反映している。 バルジの3領域 この論文は、バルジの3領域、l = 340°, b = -15°, -25°, -35° の V = 15.5 - 21.5 での見かけ微分光度関数(スターカウント)、 カラー分布、色―等級格子を提示する。 |
2.a. 観測各領域に2種類の乾板が使われた。観測は AAT 3.9 m 望遠鏡を使って行われた。 まとめを表1に載せた。2.b. データ整約 図1a.二次標準星の V バンド写真測光等級と光電測光の比較。 |
 表1.観測のまとめ。  図1b.二次標準星の B バンド写真測光等級と光電測光の比較。 |
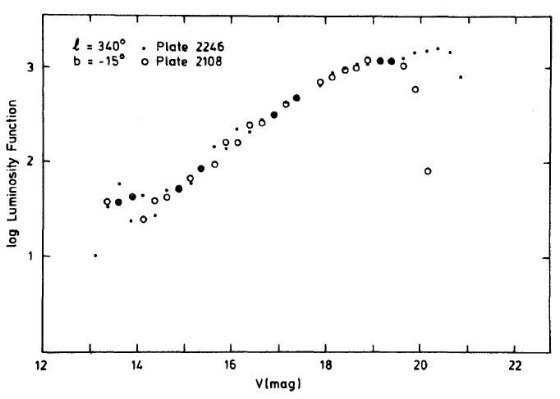 図4.l = 340°, b = -15° での微分スターカウント。 縦軸は (27 arcmin)2 領域内の ΔV = 0.25 mag 区間内星数。 図4−6は各領域の V 等級スターカウントである。測定は2枚の乾板で独立に行われ、 それぞれを示した。限界等級へのシーイング効果が良く分かる。 |
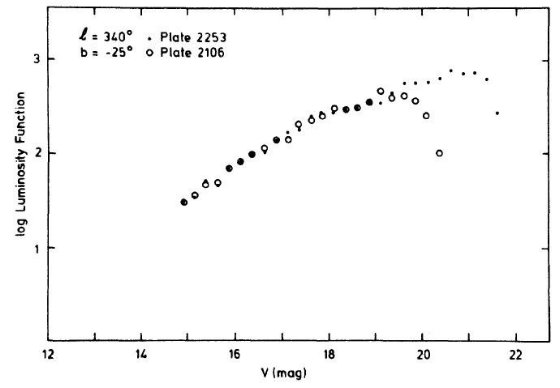 図5.l = 340°, b = -25° での微分スターカウント。 縦軸は (27 arcmin)2 領域内の ΔV = 0.25 mag 区間内星数。 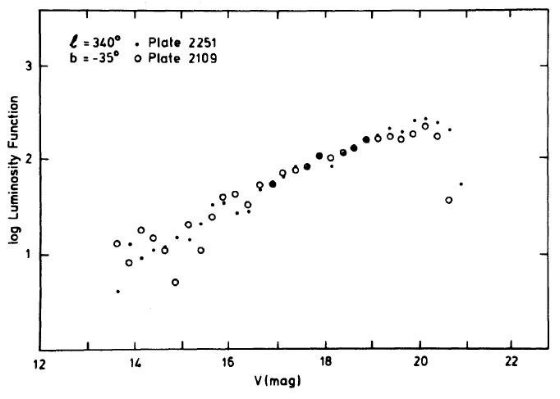 図6.l = 340°, b = -35° での微分スターカウント。 縦軸は (27 arcmin)2 領域内の ΔV = 0.25 mag 区間内星数。 |
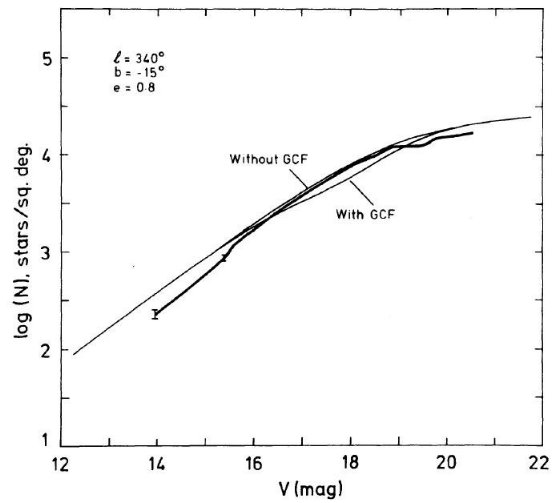 図8.l = 340°, b = -15° での微分スターカウント。太線=観測。 細線=バコール・ソネイラモデル。二つは楕円体光度関数に球状星団的特徴を 入れたかどうか。 4.a. スターカウント光度関数B-S モデルは銀河系の様々な領域で見かけ光度関数とカラー分布を説明するのに 目覚ましい成功を収めた。最近では、楕円成分用の光度関数により現実的なものを 使うようになった。この関数には有名なサルピータ不連続が現れている。 観測とモデルとの比較 B - S モデルでは、楕円体成分に球状星団特徴を取り込み、ダスト吸収層も含 んでいる。比較用に球状星団特徴を抜いたラインも計算した。モデル計算には バコール氏より提供されたコードを使った。観測結果は V = 15.0 - 21.0 で モデルに強い制約をもたらす・ モデルとの一致、不一致 図 8 - 10 の観測データは 25 % 精度内では B - S モデルで良く説明されている。 しかし、観測スターカウントには楕円成分に球状星団特徴を加えたことによる効果 が見えていないことは明らかである。図を見ての初めの判断は球状星団特徴は存在 しないということであろう。しかし、後に論じるがそれは少し早計である。 注意しておくが、我々は B-S モデルによって議論しているが、古い「厚い円盤」を 含めた Gilmore,Reid 1983 もまた強い球状星団特徴を持つ定性的に類似した 光度関数を予言する。また、銀緯が高くなるに連れ、観測星数が B-S モデルより 少なくなっていく系統的な傾向がある。円盤スケール高の僅かな変更や、異方性 の導入など、モデルの調節によりこれらの差異は解消できるだろう。それは今後の 課題である。 窪みがあるはずがコブ 図を調べると、B-S モデルに対して、スターカウントでは V = 15 - 18 mag 帯、 球状星団特徴によるとされる窪みのところで星数の超過が見られる。 |
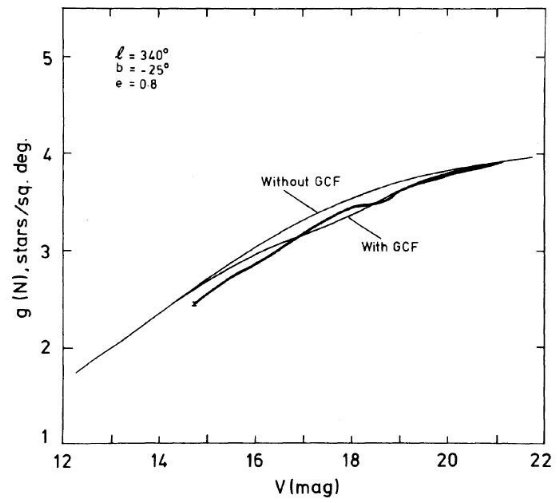 図9.l = 340°, b = -25° での微分スターカウント。太線=観測。 細線=バコール・ソネイラモデル。二つは楕円体光度関数に球状星団的特徴を 入れたかどうか。 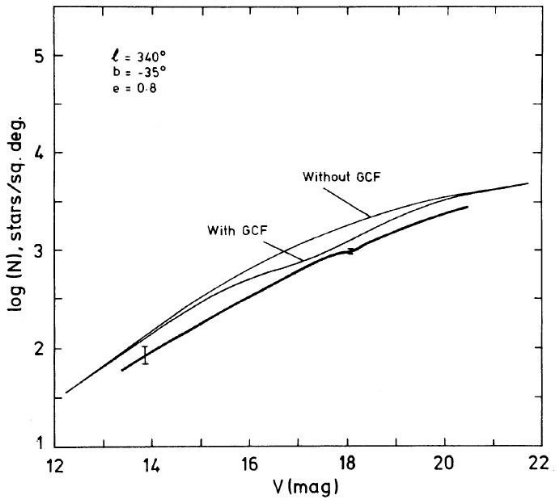 図10.l = 340°, b = -35° での微分スターカウント。太線=観測。 細線=バコール・ソネイラモデル。二つは楕円体光度関数に球状星団的特徴を 入れたかどうか。 |
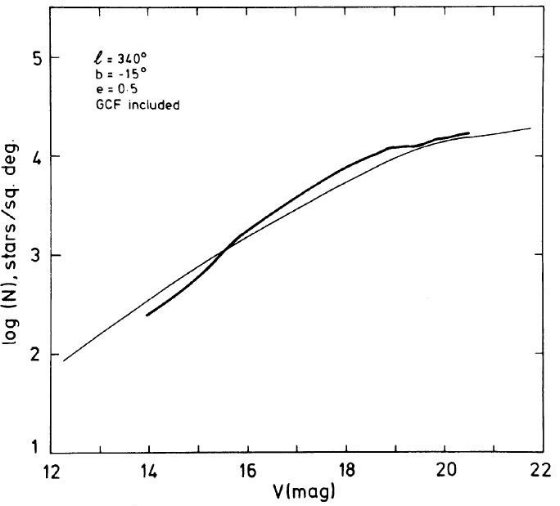 図11.l = 340°, b = -15° での微分スターカウント。太線=観測。 細線=バコール・ソネイラモデル。ただし、 e = 0.5 と扁平度を上げた。 扁平楕円体成分はもっと合わない B-S モデルは高銀緯観測から、楕円体成分の e = 0.8 とした。我々は銀河中心距離 3 - 5 kpc の所では扁平度がより大きいかも知れないと考え、e = 0.5 のモデルと 比べた。しかし結果は一層ひどかった。この場合、円盤星が卓越してくるので、 楕円成分の球状星団特徴による窪みは消える。 |
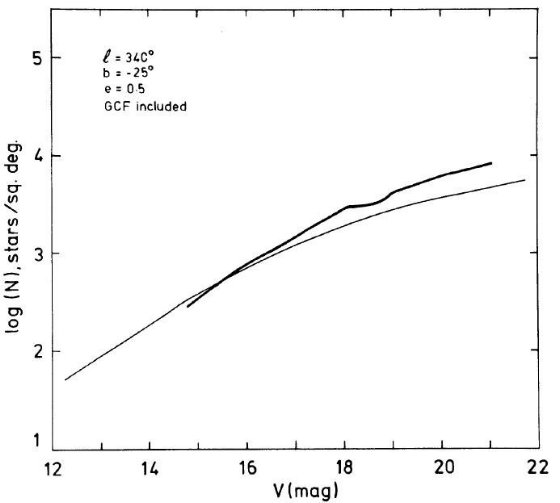 図12.l = 340°, b = -25° での微分スターカウント。太線=観測。 細線=バコール・ソネイラモデル。ただし、 e = 0.5 と扁平度を上げた。 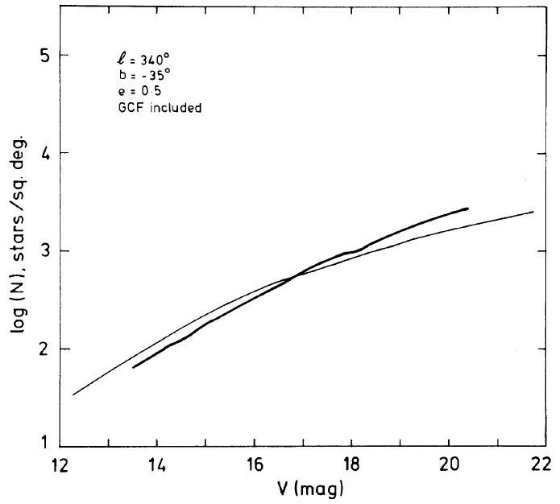 図13.l = 340°, b = -35° での微分スターカウント。太線=観測。 細線=バコール・ソネイラモデル。ただし、 e = 0.5 と扁平度を上げた。 |
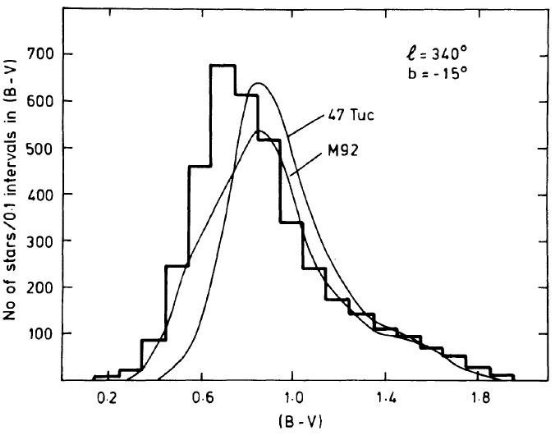 図14.l = 340°, b = -15°、V < 20.5 星のカラー分布。B-S モデルの方は楕円体成分に M92 と 47 Tuc ヘスダイアグラムを使用して計算。 規格化 B-S モデルの方は楕円体成分に M92 と 47 Tuc ヘスダイアグラムを使用して計算した。 規格化は 1.3 < B-V < 1.5 で観測とモデルが重なるようにした。これは、円盤矮星 を一致させたことに他ならない。-35° 領域は B-V > 1.5 の円盤矮星が欠落して いることを示す。しかし、これは青乾板の不完全性によるものである。しかしこれは 規格化には関係ない。 減光 分布の赤い外枠がモデルと合っていることは選んだフィールドが 一様な減光を受けていることを示す。-15°, -25°, -35°, での赤化は E(B-V) = 0.20, 0.12, 0.07 である。観測カラー分布は青成分が銀緯と共に系統的に 欠落して行く。 クソー。ひどい英語だ。死んじゃえ。 B−V=0.5成分の変化 -35° では B-V = 0.5 付近で大きく欠落しているが、 -15° では逆に大きく 超過している。興味深いのは -25°, -35°, での赤い方の分布が M 92 モデルで 良くフィットされている点である。後に、カラー分布の青色成分(B-V=0.5)のピークが 銀緯で変わることから示唆されるバルジの種族勾配は、色等級図にも現れている 事を論じる。 |
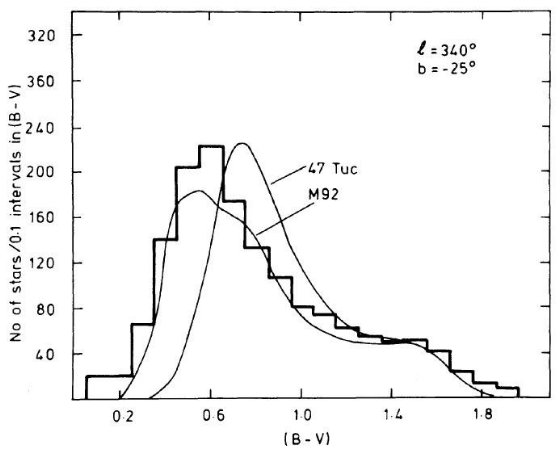 図15.l = 340°, b = -25°、V < 20.5 星のカラー分布。B-S モデルの方は楕円体成分に M92 と 47 Tuc ヘスダイアグラムを使用して計算。 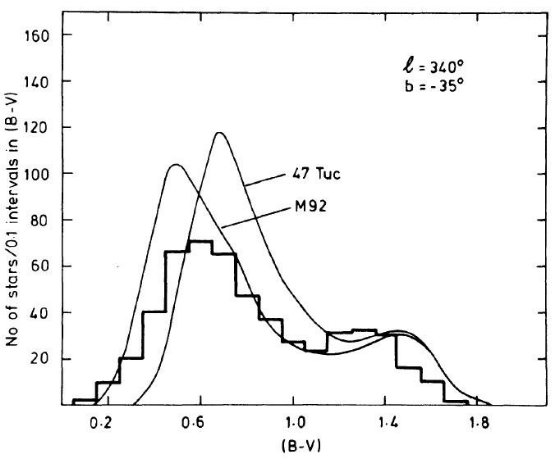 図16.l = 340°, b = -35°、V < 20.5 星のカラー分布。 B-S モデルの方は楕円体成分に M92 と 47 Tuc ヘスダイアグラムを使用して計算。 |
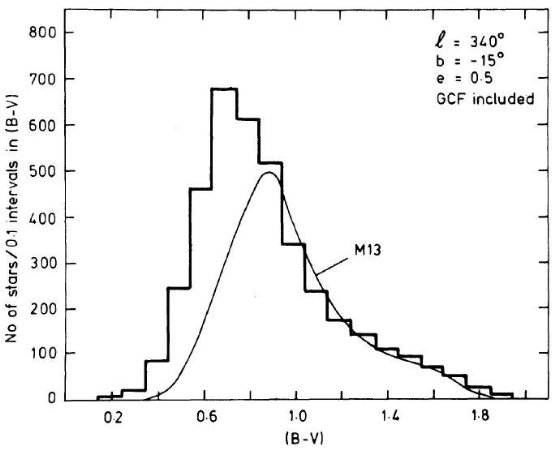 図17.l = 340°, b = -15°、V < 20.5 星のカラー分布。e = 0.5 とした点以外は図14と同じ。 さらに、円盤とバルジ星の相対比が銀緯に応じて激しく変わることを注意する。 b = -15° では円盤成分が支配的になる。図17−19ではカラー変化に 楕円成分の扁平率がどう影響するかを見るため、 e = 0.5 の場合のカラー分布を 比べた。混乱を避けるため、低メタル星団 M 13 のみを比較用に用いた。楕円体 成分の寄与が小さくなったために、どの銀緯でも青ピークの超過が見られるが、 全体のフィットは良くない。 結局のところ、B - S モデルに対する超過は円盤成分に起因すると言う結論に なった。 なに言ってんだか。 |
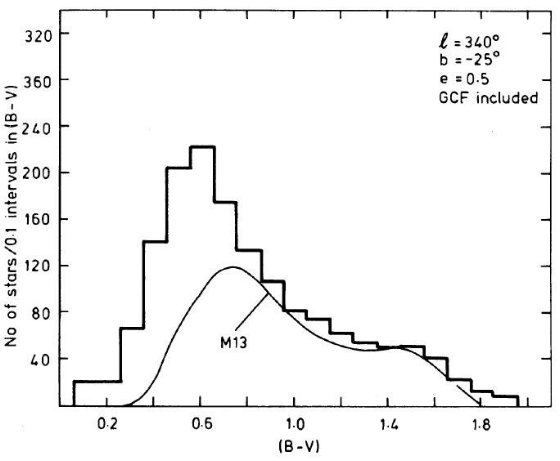 図18.l = 340°, b = -25°、V < 20.5 星のカラー分布。e = 0.5 とした点以外は図14と同じ。 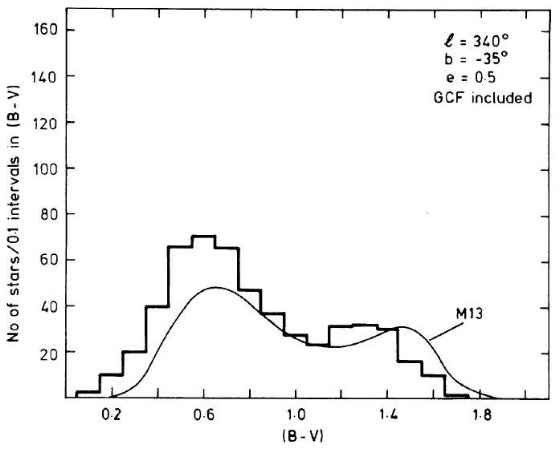 図19.l = 340°, b = -35°、V < 20.5 星のカラー分布。e = 0.5 とした点以外は図14と同じ。 |
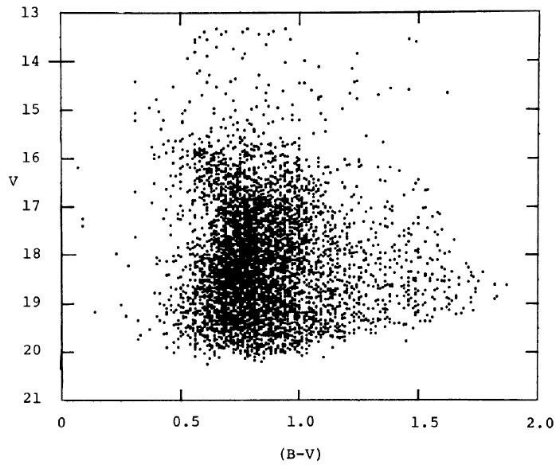 図21.l = 340°, b = -15° の色等級図 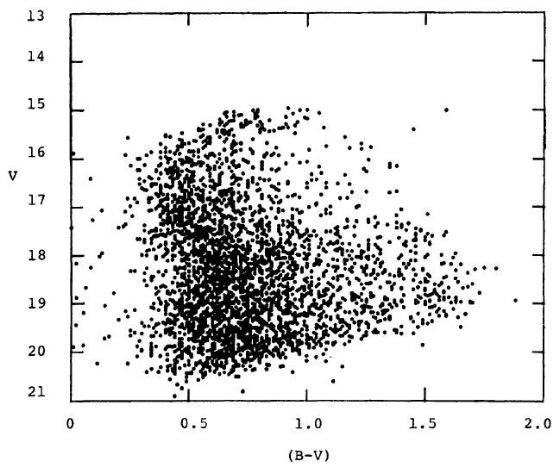 図22.l = 340°, b = -25° の色等級図 表面密度 図20には指数関数分布の円盤の表面密度と距離指数の関係を示した。図には 極大の存在が示されている。その効果が見かけ等級と色の図に現れているだろう。 図21−23に色等級図を示す。等級エラーが 0.11 等と大きいので図の分散が 大きい。 色等級図の特徴 銀河系中心距離を 8 kpc, バルジのスケール長 2.2 kpc とすると、バルジの半分密度 点の間の距離指数は 5*log[(8+2.2)/(8-2.2)] = 1.2 である。我々の色等級図にはこの 巾が現れているはずである。色等級図には次の特徴が見られる。 (1)V < 17.5 に円盤主系列星のバンドがある。異なる距離の星が混じり合って ぼけているが、赤い星ほど低光度の傾向がある。 (2)V > 18 では明らかに先端が切られた主系列と円盤主系列を横切る 準巨星が見える。我々はこの集団をバルジと看做す。 |
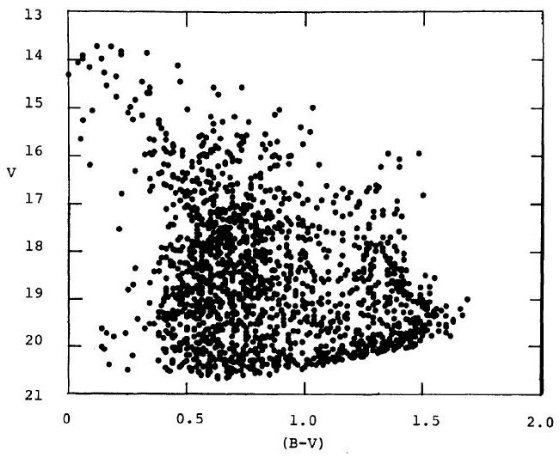 図23.l = 340°, b = -35° の色等級図 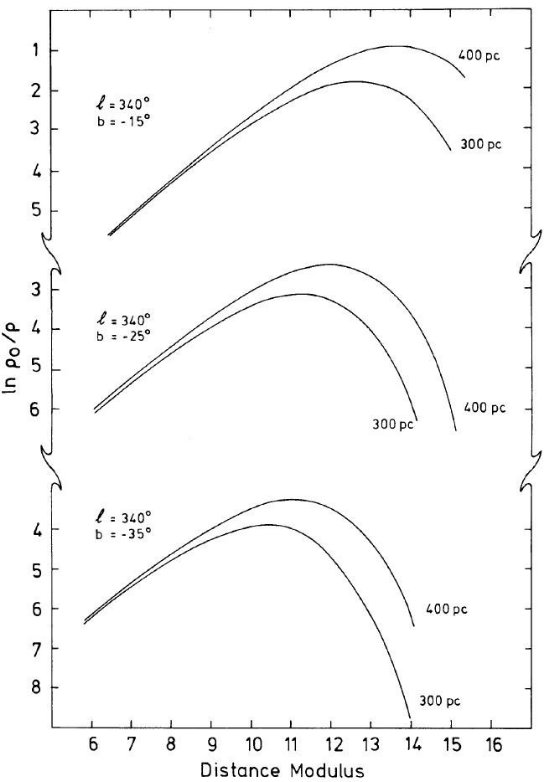 図20.円盤星の表面密度と距離指数の関係。円盤スケール長は 3.5 kpc, スケール高は 300 pc と 400 pc の二つを撮った。 |
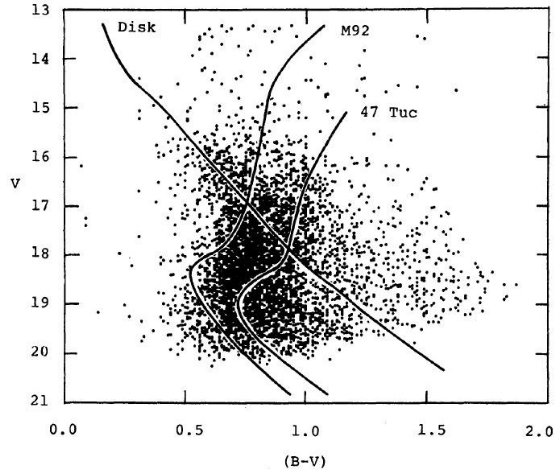 図24.l = 340°, b = -15° の色等級図上に円盤主系列を 円盤星の尾根に置いた。M92 と 47 Tuc のラインをバルジ星分布に 合うよう置いた。赤化は B - S モデルを適用。 フィット円盤星 図24−26には、色等級図上に円盤主系列およびバルジ主系列と準巨星 を重ねた。円盤主系列のフィットはスケール高 370 pc に対応する。これは 古い円盤種族に対応するスケール高である。フィットされた円盤主系列星は 15 < V < 18, 0.3 < (B - V)o < 0.5 であり、スターカウント の窪みをを埋めた星と考えられる。 フィットバルジ星 バルジターンオフ付近の尾根線は b = -25°, -35° では M 92 が ベストフィットとなるが、 b = -15° では 47 Tuc の方が良く合う。 ただし、B-H 赤化の予想と比べ、図24−26は b = -15° で 0.2 mag 赤い。これはメタル量勾配があり、銀河系中心付近では高メタルになっている ことを示している。 銀河中心距離 フィットからバルジ星の平均距離指数は 14.4&plumn;0.5, 幾何学的補正を 加えて銀河中心距離は 8.4±2.0 kpc となる。 |
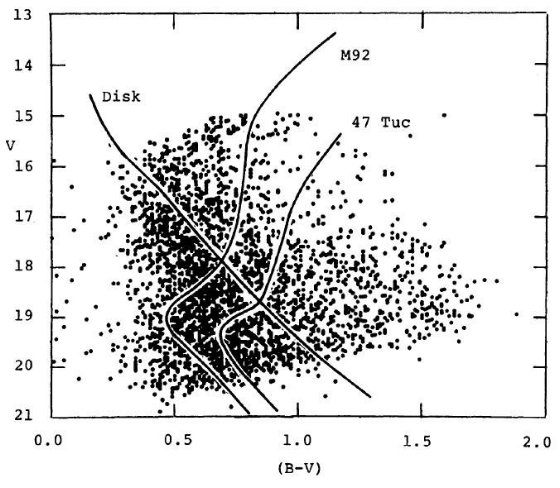 図25.l = 340°, b = -25° の図24対応図。 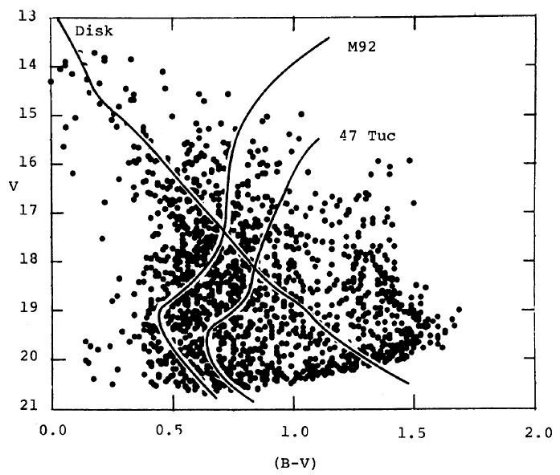 図26.l = 340°, b = -35° の図25対応図 |