| R, I, J, H, K, L, [12], [25] バンドでの銀河系星計数モデルを 任意の方向、感度で与えるモデルを作った。銀河系は、Hernquist 密度則に従う 楕円体成分、スケール高 100 pc と 390 pc の二つの円盤、それに渦状腕の 重ね合わせで作った。V - λ 色指数から各光度クラスとスペクトル帯の 絶対等級をスペクトル型の関数として多項式の形で求めた。星間減光は原子、分子 ガスの分布から求めた。晩期型巨星、超巨星星周ダストからの寄与も考慮した。M6 より晩期の巨星は全てダストシェルを持つことが分かった。 | でーたが不足しているため、全てのバンドでモデルと観測との比較は行えなかった。 K バンドでは 1 - 11 等までの比較を様々な方角で行った。モデルは全方向で適切な 星計数を与えた。また、 [12], [25] での比較も良かった。ただし、IRAS バンドで は渦状腕を表すのに余分のパラメタ―を必要とし、それでも局所腕の表現は良く なかった。円盤のスケール長は 390 pc 円盤に対しては 2.6 kpc, 100 pc 円盤では もっと大きく 4 kpc であった。Ro = 7.9 kpc を採用した。 |
２．１．回転楕円体成分回転楕円体成分は Hernquist 1990 の表式で表す。
ここに、a = スケール高、s = スペクトル型の数値表現で、 O5 で 0.5, B0 で 1.0, M0 は 6.00, M7.5 は 6.75 である。 |
２．２．二つの円盤成分
ここに、nd,i(Ro,0,s)は太陽近傍(r=Ro, z=0) s-スペクトル星の 数密度。i = 1(薄い円盤)、2(厚い円盤）。αr(i) = 円盤スケール長はスペクトル型に依存しないと仮定する。 |
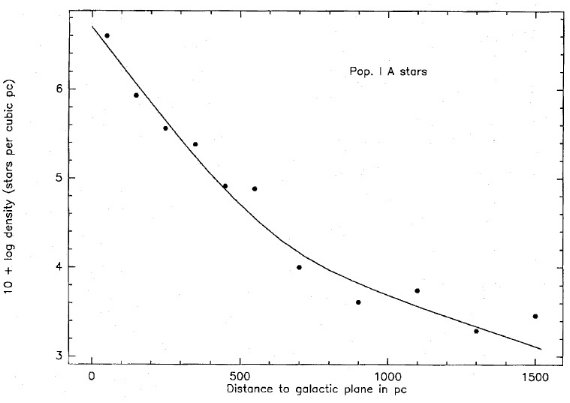
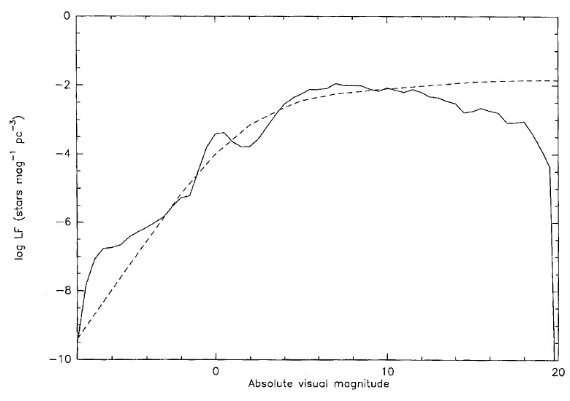
 図１．種族I, A 型星の密度 [10 + log(星/pc3)]の銀河面高度に よる変化。データは Lance 1988 より。フィット曲線は 0.5×10-3exp(-z/100)+6×10-6exp(-z/390)  図３．太陽近傍の光度関数。図２から計算。 破線＝ Bahcall, Soneira 1980 の使用した光度関数。 |
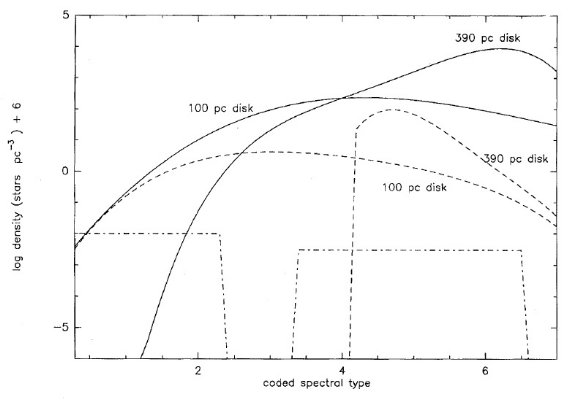
 図２．太陽近傍でのスペクトル型分布。密度は 10-6 星/pc3/ δs=0.1 の対数で表示。二つの円盤毎に密度を示した。実線＝主系列星、 点線＝巨星、一点鎖線＝超巨星。 |
２．３．渦状腕 表１．渦状腕の接線方向  図４．銀河系の渦状構造。曲線＝４本腕モデルでの密度極大の軌跡。 破線＝"spur". 直線＝接線方向。 |
 表２．コード化スペクトル型による、V 絶対等級とカラーの多項式表示係数 |
 図５．コード化されたスペクトル型による V-R カラーの変化。  図７．コード化されたスペクトル型による V-J カラーの変化。  図９．コード化されたスペクトル型による V-K カラーの変化。  図１１．コード化されたスペクトル型による V-[12] カラーの変化。 |
 図６．コード化されたスペクトル型による V-I カラーの変化。  図８．コード化されたスペクトル型による V-H カラーの変化。  図１０．コード化されたスペクトル型による V-L カラーの変化。  図１２．コード化されたスペクトル型による V-[25] カラーの変化。 |
 図１３．コード化されたスペクトル型による K-[25] カラーの変化。 三角＝ダストシェルの付いた星。四角＝ダストシェルのない星。 K-[25] = 0.7 のギャップが二つの境界である。 |
 図１４．コード化されたスペクトル型による ダストシェル付き星の割合の変化。 |
 図１５．HI と H2 の銀河中心距離による密度変化。 |
 表３．H と H2 密度の多項式表示の係数。 |
 図１６．星計数 (星/deg2) の銀経による変化。限界等級 K = 8(上) と 10(下)。データ点は Eaton et al 1984 による。 |
 図１７．４方向での 星計数 (星/deg2) の K 限界等級による変化。 |
 図１８．図１７と同じ。 |
|
|
|
|
|
|
|
|
|