|
計算の特色 TP-AGB 進化を Z = 0.0001 から 0.03 まで 7 種類、初期質量 0.5 から 5 Mo, について計算した。この計算に取り入れられた最新の進展は、 (1)TP-AGB 期の静謐光度、熱パルス間隔、第3ドレッジアップ、ホットボトム バーニング、パルスサイクル光度の解析的関係を詳細にし、改訂した。 (2)光球大気の化学組成が変化するにつれてオパシティを変えた。 (3)C-, O-リッチ AGB 星の脈動するダスト駆動星風モデルから導かれる質量 放出率を定式化して進化計算に取り入れた。 (4)進化途中で脈動の基本振動モードから第1励起モードへの転換を導入し、 質量放出率をそこで大きく変化させた。 |
計算改良の結果 以上の改良の結果、HR図上での進化以外に、 (1)表面化学組成の変化 (2)脈動モードと周期 (3)質量放出率 を矛盾なく予言できるようになった。第3ドレッジアップの開始時期と効率は マゼラン雲炭素星の光度関数とマゼラン雲星団中の AGB 星寿命を再現するよ うに較正した。 第1論文の重点 この論文ではオパシティ変化による影響を提示することに重点をおいた。次の 論文で等時線等について論じる。 |
|
合成進化モデル TP-AGB 進化計算はまだ M- から C-型への転換を Mi = 1.5 Mo, Mbol = -3.5 で引き起こすことには成功していない。観測に関しては Herwig 2005 を見よ。 計算面では複雑な内部構造、ドレッジアップ、質量放出が問題となっている。 この難点を回避するため合成進化モデルが考案された。そこでは、完全なモデル 計算に基づいて得られた簡単な関係式により進化が記述され、一方ドレッジアップ とマスロスは調整パラメターにより最適化される。 最近の進展 この論文は最近起きた以下3点の進展が引き金となって書かれた。 (1)最近の理論的進展 最近の理論的進展により(Wagenhuber,Groenewegen 1998, Karakas et al 2002, Izzard et al 2004) TP-AGB 期の Mc - L 関係、熱パルス間隔、パルスサイクル 変化、ドレッジアップ効率に関する解析的関係の適用範囲は著しく広がった。 マスロスのモデル(Wilson 2000, Winters et al 2003, Hofner et al 2003) も 大きく進展した。その上、Marigo et al 2002 はそれまで使われていた低温 オパシティは、ドレッジアップにより元素組成が変化することに伴う、分子密度 の変化を考慮していなかったので大きなエラーが含まれることを示した。適切な 分子オパシティの導入の結果、星が炭素リッチになった際に大きな変化が生じた。 これらの理論的進展は TP-AGB 進化の多くの面でより良い記述を可能にする。 (2)赤外サーベイ NIRカメラの観測によりマゼラン雲では炭素星の「赤い尾」(Cioni et al 1999, |
Nikolaev, Weinberg 2000) が発見され、炭素星サーベイ(Battinelli, Demers 2005) と
将来の UKIRT, VISTA を使ったサーベイは局所群銀河の TP-AGB 星の完全サンプル
を提供するであろう。一方、IRAS, ISO, Spitzer による MIR サーベイはダスト
に覆われた LMC 星のサンプル (Loup et al 1999, Cioni et al 2003, van Loon et
al 2005, Blum et al 2005) を提供している。現在のデータセットで何ができる
かの例が Cioni et al 2006a,b に見られる。彼女らは NIR データを進化モデル
と比較する手法のみで LMC と SMC を横断してメタル量と星形成率が変化している
ことを示した。 (3)P - L 多重系列 MACHO, OGLE はマゼラン雲と銀河系バルジ内にある長周期変光星の可視光 変光データを提供した。その結果、P - L 多重系列の発見である。その内 4つは AGB, 上部 RGB 星の脈動モードに対応している。(Wood et al 1999, Soszynski et al 2006, Ita et al 2004, Fraser et al 2005) 明らかに TP-AGB 星は初め小振幅の SR (第1、第2励起振動)として出現し、その後 大振幅のミラ(基本振動)となる。一般に、脈動周期はマスロス率と相関がある ことは一般に信じられており、上の事実は進化の上で重要でありさらに追及 されるべきである。 論文の内容 我々はこの様な進展を取り入れて TP-AGB モデルを作る。合成進化モデル の常として、不確定パラメターは観測事実、マゼラン雲炭素星の光度関数と マゼラン雲星団内 AGB 星の寿命、により調整される。第2段階として、 周期分布や各脈動系列にある星の数の比、ダスト星の性質なども チェックに使うつもりである。 |
|
TP-AGB 合成モデルの発展 TP-AGB 星の合成進化モデルが Marigo et al 1996, 1998 により開発された。 そこでは、Mc - L 関係や熱パルス間隔などの関係式がパラメターを入れた ドレッジアップの記述、大気モデルの積分と組み合わされていた。その後、 幾つかの点で進展があった。それらは、 (1) 対流層底部での水素燃焼が原因のオーバーシューティングとそれに関連 する核合成(HBB)の発展。 (2) 対流層基底部のフラッシュ後での最低温度 Tbdred に関連した物理的に 基礎がしっかりしたドレッジアップパラメターの採用。二つのパラメター、 一つはドレッジアップ発生に関連する Tbdred で、もう一つ λ は第3ド レッジアップの効率を表わす、はマゼラン雲炭素星の光度関数により 調整される。(Marigo et al 1999) (3) 実際の元素組成に対応した分子オパシティ κvar の計算。以前は太陽 組成のオパシティ κfix が使われていた。 合成進化モデルの一般的な説明は Groenewegen, Marigo 2003 に詳しい。 |
2.1.初期条件第1熱パルス開始時の物理量最初の熱パルスにおける初期条件、つまり全質量、光度、コア質量、第1、第2 ドレッジアップ後の表面組成、は Z = 0.0004, 0.001, 0.004, 0.008, 0.019, 0.03 について、Girardi et al 2000 より得た。Z = 0.0001 については、Girardi 2001(unpublished, http://pleiadi.oapd.inaf.it を見よ) が計算した進化を 用いた。これらの計算は OPAL (Iglesias,Rogers 1993) と Alexander,Ferguson 1994 オパシティを用いた。対流核のオーバーシューティングは穏やかな強さの ものを採用した。このオーバーシューティングの結果、AGB が現れる質量上限 は、全ての Z に対して、普通採用されるモデルでの 8 Mo の代わりに 5 Mo と なった。しかし、炭素燃焼の初期段階が詳しく追跡されなかった(Girardi et al 2000, Sect.3.1.)のでこの値はやや不確かである。そういう訳で、この論文では 5 Mo を 考慮される最高質量とした。 この論文での初期質量の使い方 最後に、この論文では初期質量を第1熱パルスが起きる時の意味で使用して いることを注意しておく。というのは Girardi et al 2000 の前駆 AGB 期進化 が質量一定の仮定で計算されているからである。低質量星で RGB 期での 質量放出が進化に及ぼす影響は等時線を作る際には後付けの形で考慮する。 (Marigo, Girardi 準備中) |
2.2.光度とコア質量の成長計算改善の目的今回の計算では下の2点を追うため新しい改善が加えられた。 (1) 光度の進化 L(t) (2) コア質量の成長率 dMc/dt = LHQH/X(H) ここに、 LH は水素燃焼殻の光度、QHは水素単位質量当たり 水素燃焼によるエネルギー発生率、X(H) は水素組成、である。 上の式は LH / [ QH X(H) ] の間違いじゃないか? Mc - L 関係の選択 この目的に使用するため、色々な文献の中から適切な Mc - L 関係を選ぶ必要が ある。合成進化モデルでキーとなるこの関係は、通常 AGB 完全進化モデルの計算 から、静謐期のフラッシュ直前極大光度をコア質量の関数としてフィットし、 そこにメタル量、外層質量、第1熱パルスの初期条件などを加味して導かれる。 何を言っているのか理解できない。 HBB が起きない低質量モデルでは、Wagenhuber,Groenewegen 1988 の Mc - L 関係を採用した。これにはメタル量依存性や初期条件による特異な振る舞いの 効果が含まれている。 より重い、Mi > 3.5 - 4.5 Mo (数字はメタル量に依る)で HBB による超過 光度のある星に対する Mc - L 関係は、Izzard et al 2004, 32 式の付加項を 足すことにより得た。これは、仮に深いドレッジアップ(λ &asympt; 1) のため Mc が一定であったとしても核の縮退度が進行するにつれ L は上昇して いくことを意味する。 Wagenhuber, Groenewegen 1988 式の導入 Mc - L 関係が厳密に成り立つのは熱パルス直前の静謐光度の時であり、 大きなずれ、例えば急速な落ち込み、急なピーク、ゆっくりした光度低下、など フラッシュの発生とそれに伴う力学的構造変化、熱緩和に起因する変動がパルス |
間時期には起きる。我々の以前のモデルでは、急な立ち上がりとゆっくりした緩和
という単純な変化しか考慮しなかった。今回は、Wagenhuber, Groenewegen 1988 の
定式化の助けを借りて、パルスサイクルの間の L(t), LH の激しい変化
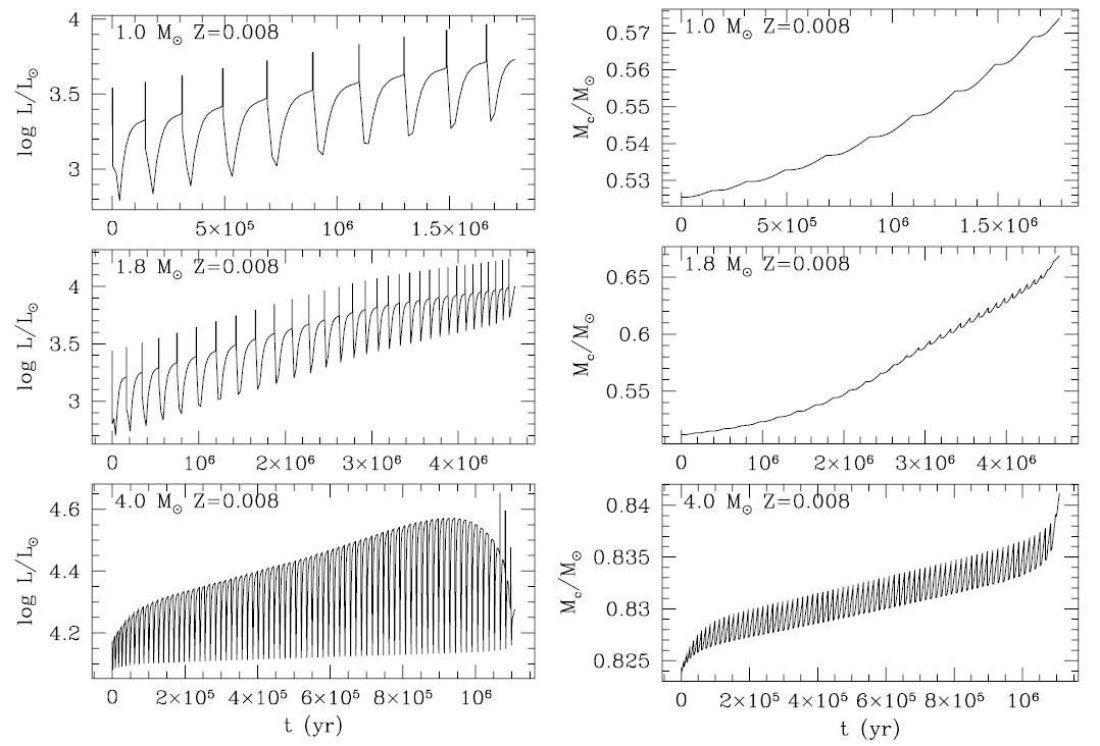
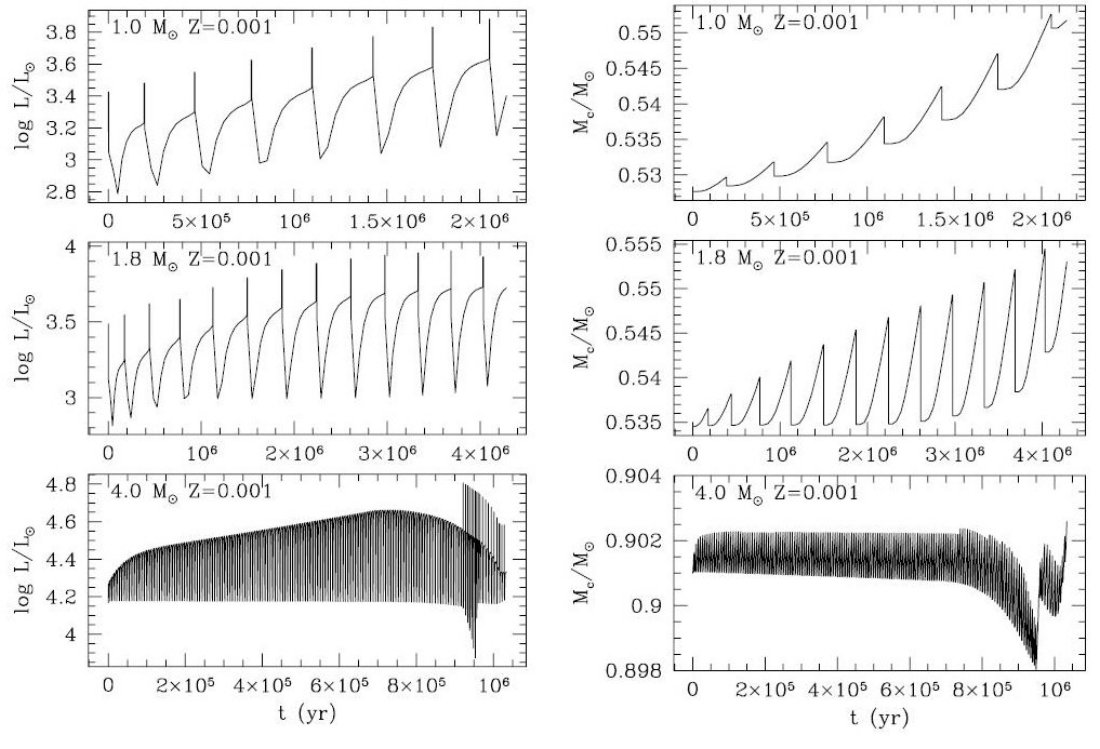
を時間的に追うようになった。 熱パルスによる L 変化 図1、2には L の詳しい変化の例を示した。これらの結果は TP-AGB の 完全計算 Vassiliadis, Wood 1993 図 4 - 9、と較べると良く一致する。 4 Mo の場合、外層質量が大きくなるため、最後の大規模質量放出期を除き、熱 パルスによる L の変動は大きくないことに注目して欲しい。また、この質量 では HBB のため Mc - L 関係を上まわる光度を示す。 コア質量の鋸状変化 注意すべきは、間パルス期に水素燃焼によって増大したコア質量は熱パルス の際に起こるドレッジアップにより削られるということである。このように 繰り返される増加と減少の結果、コア質量の時間変化は図1,2の右側に示さ れるように鋸状となる。例外は、Z = 0.008, M = 1 Mo でドレッジアップが起 きない。これらの図を見ると容易に判るが、対流ドレッジアップは質量が大きく なり、メタル量が低いほど起こりやすい。 様々な仮定に基づく計算の例 表1には M = 1.8 Mo, Z = 0.008 での4つの合成 AGB モデル計算例 A, B, C, D を示した。計算に際しての仮定は、光度変化を詳しく追う L(t) か、静謐 Mc - L 関係を使うか、スケール太陽組成でのオパシティ( κfix ) か、組成変化を考慮するか( κvar )、ドレッジアップを入れ るか入れないか等の組み合わせである。 表に載っている他の量は、 τTP-AGB = TP-AGB 寿命、 τM = M-型 星寿命、 τC = C-型星寿命、 Mf = 最終質量、 C/O = 最終 C/O 比、 Teff(SW) = 超星風開始時の有効温度である。 モデル A はこの論文で採用された仮定である。間パルス期に Mc - L 関係を 採用したモデル B はもでる A と全く異る結果となった。実際、どちらも最終 質量の点では殆ど同じ値になったが、TP-AGB 全期間、M-型星期間、C-型星期間 の全てでモデル B は 30 ∼ 40 % 短い。モデル C はドレッジアップを 抑えた結果、TP-AGB 期間が大幅に縮まった。また 当然 C-型星は出来なかった。 この結果を見ると、例えば銀河内での TP-AGB 星の数の予想値は採用される 仮定により大きな影響を受けることが予想される。 |


2.3.間パルス期パルス間隔 τip 熱パルスが刻まれる速さを規定する。この 計算では Izzard et al 2004 の式を採用した。これは Wagenhuber, Groenewegen 1988 の Mc - τip 関係の改訂版である。Wagenhuber, Groenewegen 式は 深いドレッジアップを伴う重い星で見られる τip の増加を説明 するが、 Izzard et al 2004 では加えて、ドレッジアップ効率 λ も 含まれるようになった。2.4.有効温度分子オパシティ有効温度は光球からコアまでの大気モデルの積分の助けを借りて求められる。 積分のやり方は Marigo et al 1996, 1998, 1999 に述べられている。外層積分の 結果は有効温度である。注意しなければならないのは低温における分子の 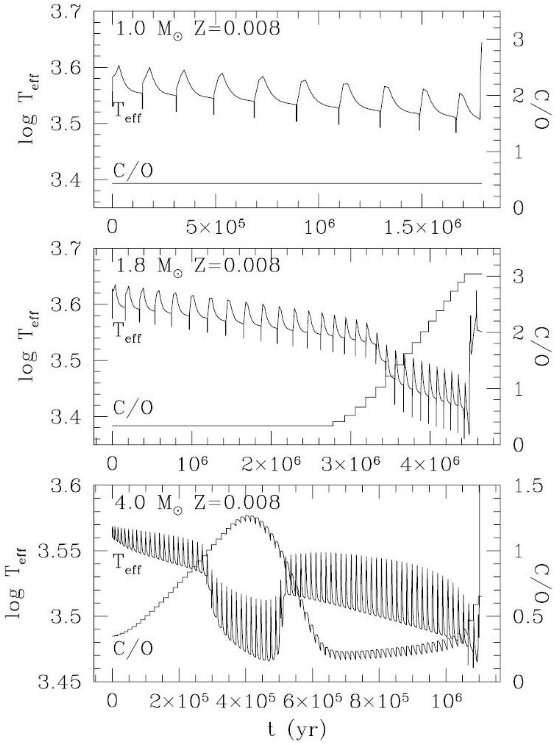 図3.図1と同じく Z = 0.008 のモデルの有効温度と C/O 比の変化。 熱パルス直後 L が底値の時に Teff が上昇し、間パルス期に L がゆっく り上がるにつれ、Teff は下がって行くことに注意。C/O が 1 を越えた時 の Te の低下も目立つ特徴である。4.0 Mo では逆に HBB の結果 C/O が再低下するのに伴い Te が上がる。 |
有効温度 オパシ ティである。そしてここで重要な点は我々はスケール太陽組成のオパシティ κfix を棄てたという点である。こうして我々は 酸素リッチ から炭素リッチな大気表面に移る際の大きなオパシティ変化を考慮できるように なった。 図3、4は有効温度と表面 C/O 比の時間変化を示す。熱パルスは準周期的な Te 変化を引き起こすが、それは基本的には L の鏡像となっていることが図1,2 と比較すると判る。κvar の導入に取り、C-リッチになったとた んに Teff(t) カーブが変化することが判る。対照的に、Mi = 1 Mo, Z = 0.008 のように第3ドレッジアップが起きないモデルでは、Teff が単調に低下 していく。Mi = 4 Mo, Z = 0.008 では C/O < 1 から C/O > 1 さらに C/O < 1 へと変化する。これはドレッジアップと HBB との競合の結果である。 変化オパシティ 前に述べたように、Marigo 2002, Marigo et al 2003 では、化学的に変化 する分子オパシティを採用して、炭素星進化の計算を大きく改善した。その結果、 長い間問題とされていた観測と理論の矛盾が解消した。例えば、マゼラン雲の 二色図で見られた赤い尾が再現され、また銀河系炭素星で見られた低い C/O 比 や Teff が得られた。 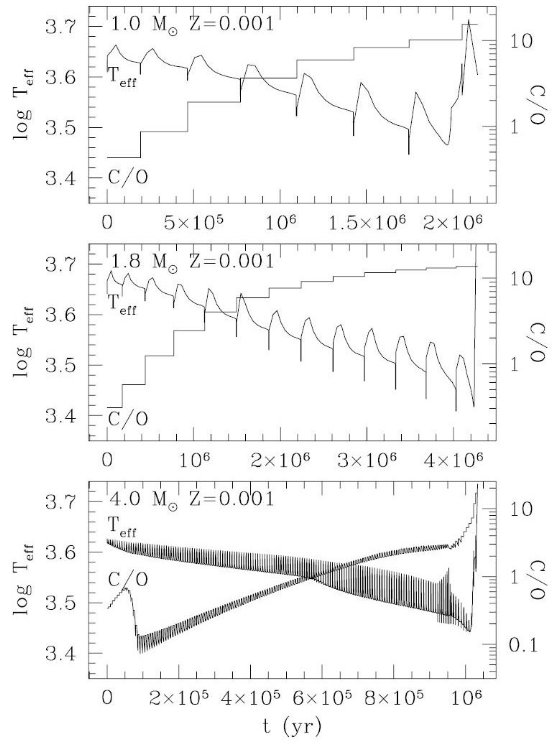 図4.図3と同じだが、Z = 0.001 |
|
κvar と炭素星寿命 炭素星のこのような性質は、実際の表面組成から分離した分子オパシティ κfix を使っていては再現することができない。図5には κfix と κvar の差を示した。 κfix の場合 Teff が C/O の逆転に影響されないが、 κvar では炭素星になると Teff 低下速度が上昇することが 見て取れる。その結果、他の入力パラメターが同じ場合に TP-AGB 寿命は κvar の方が短くなる。 メタル量効果 メタル量の効果はどうだろうか? 低メタル AGB 星大気では分子形成は 低調であろうから、炭素星大気でも分子オパシティの冷却効果はそう効かない のではないかと考えられる。例えば、図3と図4を比較すると、炭素星になった 時の表面温度低下率は Z = 0.008 の方が Z = 0.001 より激しくなる。 オパシティの表面構造への影響 分子オパシティは星の表面構造を大きく変える。特に 0.998 ≤ M(r)/M ≤ 1 の最外側では、 κvar が κfix を 大きく上回る。このため、Teff( κfix ) = 3281 K から Teff( κvar ) = 2729 K へと低下する。 図7には典型的な (Mi, Mc, L) の星に対し、メタル量を変えた時に C/O に対して Teff がどう変わるかをしめしたものである。C/O が 1 を越える 際の Teff 低下は高メタルでは著しいが、低メタルになるとそれ程目立つ現象 ではなくなってくる。そして、 Z = 0.0004 では殆ど認められない。 低メタルでこの効果が薄れるもう一つの原因は低メタルでは Teff が高い ためそもそも分子が形成されにくいということもある。 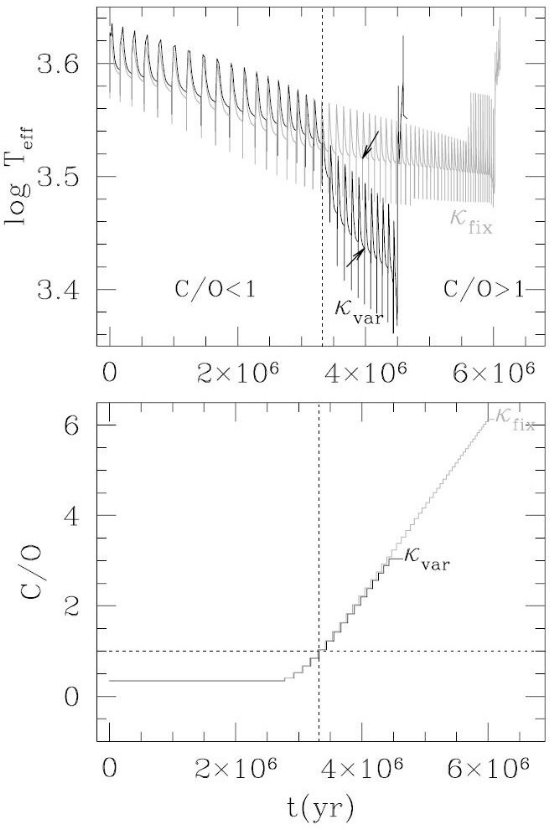 図5.Mi = 1.8 Mo, Z = 0.008 星の Te, C/O 変化。灰色=。κfix 。黒=κvar 矢印は第24回の静謐期で、図6はその時の構造。 |
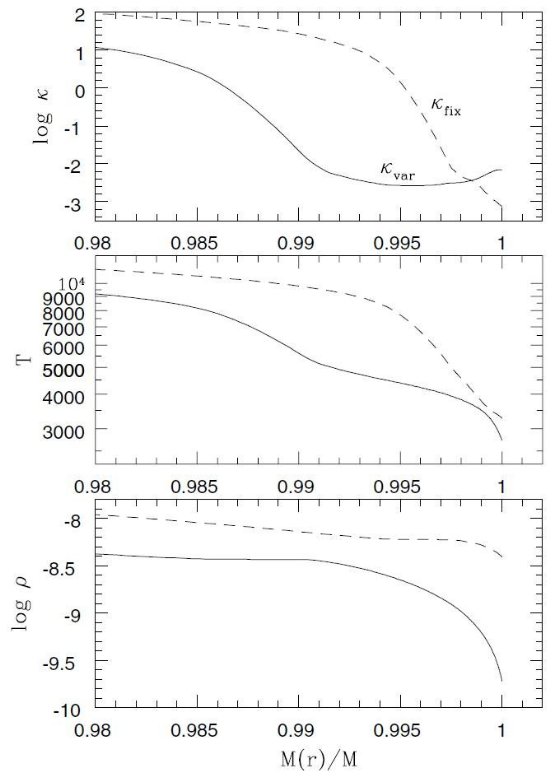 図6.M = 1.776 Mo, Mc = 0.632 Mo, log (L/Lo) = 3.926, C/O = 2.560 星の 実線= κfix と 破線 = κvar の場合の表面構造。 ロスランド平均オパシティ(cm2g-1)、温度、密度(gcm-3) 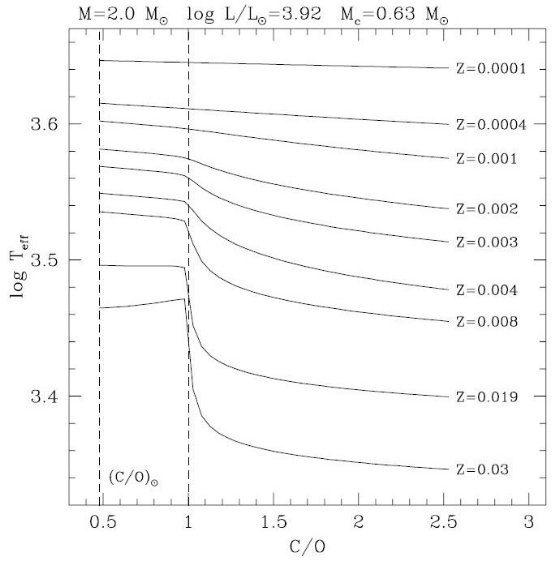 図7.C/O - Teff 関係のの初期メタル量依存性。 M = 2 Mo, log L/Lo = 3.92, Mc = 0.63 Mo を共通にした。 C/O が1を超す際の Teff 低下は高メタルほど激しい。 |
2.5.第3ドレッジアップ計算の始め第3ドレッジアップの扱いは Marigo et al 1999 と同じである。実行に当たっ ては次の3点をはっきりさせる必要がある。 (i) フラッシュ後の最高光度時期における対流層基底部の最低温度 Tb dred, 同じことだが、ミクシングを起こすのに必要な最小コアマス、 Mc min (ii) 第3ドレッジアップの効率、λ (iii) 殻の中間領域の化学組成 以前のモデル Marigo, Girardi 1999 に較べると、最近の AGB モデル Karakas et al 2002, Izzad et al 2004 のお陰で、第3ドレッジアップの計算は進歩した。 それらを次に述べる。 2.5.1.第3ドレッジアップの発生以前の方式: 固定 TbdredMarigo et al 1999 では Tbdred を、質量、メタル量 に無関係に Wood 1991 の AGB 計算に示唆されている値に固定した。マゼラン雲 炭素星光度関数から得られた値は、log Tbdred = 6.4 で あった。 今回の方式: Tbdred この論文では、log Tbdred の代わりに、ミクシングを 起こすのに必要な最小コアマス、 Mcmin という量を導入 する。これは以前から使われてきた ( Groenewegen, de Jong 1993, Marigo et al 1996, Mouhcine, Lancon 2002) 量で、総質量、メタル量に関係なく ∼ 0.58 Mo に設定されていた。最近( Karakas et al 2002, Izzad et al 2004 ) の完全 AGB モデルグリッドのお陰で総質量、メタル量に対する依存性を調べられるように なった。 この論文では、 Karakas et al 2002 が示した Mcmin (M, Z) 関係を用いる。これは、Mi = 1 - 6 Mo, Z = 0.02, 0.008, 0.004 の 完全 AGB モデルに基づいている。ただし、以下に述べる理由で部分的な変更を 加えた。 系統的シフト マゼラン雲炭素星の光度関数を再現するためには Mcmin が予想値より低い必要があった。(4.1.節)我々の合成モデルによると、その 減少量は、 ΔMcmin(Mo) = max[0.1, 0.1 - 100(Z-0.008)] 補正量、-ΔMcmin, はメタル量が増加するに連れ 大きくなる: Z = (0.008, 0.004, 0.001) に対し、補正量 = (-0.01, -0.05, -0.08)Mo である。 Z=0.008 だと -0.1Mo になるが? これは、Z ≤ 0.001 ではどの質量でも、熱パルス後に第3ドレッジアップが発生 することを意味する。実際には、M < 1 Mo の場合ドレッジアップを禁止している。これは銀河系 球状星団中のそれらの星に炭素星が見られないからである。 オーバーシューティングの補正 AGB 期以前の恒星進化に関して、 Karakas et al 2002 は水素燃焼期の対 |
流核
オーバーシューティングを仮定していない。一方、Girardi et al 2000 では
穏やかなレベルのオーバーシューティングが仮定されている。我々はそこから
AGB モデルの初期条件を採用した。 対流オーバーシューティングの重要な効果は MHeF、 すなわちヘリウム フラッシュが起きるための初期質量の最大値、を下げることである。この上限値は 初期質量 Mi と第1熱パルス時のコアマス Mc1 との関係式 での最小値で定められる。(Marigo et al 1999, Karakas et al 2002) Mcmin と Mi の間にも類似の関係が認められる。その結果、 Mcmin が MHeF に対応するのである。 ここもよく分からない。 こういう訳で、オーバーシューティングの導入は MHeF を低下させる ことになる。これは、 Mcmin(Mi) の最小値を低下させる。 言い方を変えると、オーバーシューティングの導入は近似的には初期質量 Mi の星 はオーバーシューティングなしの fovMi (fov > 1) の 星のように振る舞うのである。 Karakas et al 2002 と Girardi et al 2002 との 比較から、fov ∼ 1.2 である。対流オーバーシューティング効果を 近似的に実現するには Karakas et al 2002 関係式の Mi を fovMi で 置きかえればよい。つまり、 Mcmin(M) = [Mcmin( fovM)]Karakas02 図8には、Z = 0.019, 0.008, 0.004 に対し、上の式で決まるMc min を示した。Karakas02 に無いメタル量は Z で線形外挿した。 Mi ≥ 3 Mo では上式で決まるコアマスは第1熱パルスの時のコアマス、 Mc,1TP より小さいので、Mcmin = Mc,1TP とした。 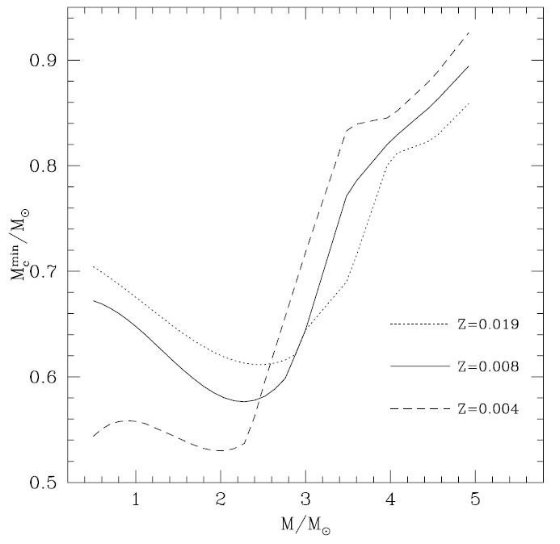 図8.第1熱パルス時に第3ドレッジアップを開始するに必要な最低コアマス。 全てのカーブで、最低値は MHeF と一致する。 |
2.5.2.ドレッジアップ効率 λλ の選択通常、ドレッジアップ効率は λ = ΔMdered/ΔMC で表現される。ここに、 ΔMdered は1回のドレッジアップで 運ばれる質量、ΔMC は前回の間パルス期間中に増加したコアマス量 である。 以前は各 Z 毎に同じ λ 値を採用していた。マゼラン雲炭素星光度関数 からの較正 Marigo et al 1999 の結果は Z = 0.008 に対し λ = 0.5, Z = 0.004 に対し λ = 0.65 であった。 λmax の M, Z 依存性 本論文では、完全 AGB モデルの結果に基づき、 λ の質量、メタル量依存性 を取り入れる。まとめて言うと、コアマスが Mcmin を越 えると λ は漸近値 λmax へと上昇していく。その様子は、 λ(N) = λmax[ 1 - exp(N/Nr) ] ここに、N は Mc > Mcmin からの熱パルス番号である。 λmax は Karakas02 の結果を近似式で表わして求めた。Z を 固定すると、λmax は Mi と共に増加して行く。M > 3 Mo で λmax = 0.8 - 1.0 である。メタル量効果は弱い。質量 Mi を固定すると、低メタルほど λmax は小さくなる。 Karakas02 λmax(M, Z) の変更 Z < 0.004 (Karakas02 の範囲外) で λmax がかなり増大 する現象を表わすため、Karakas02 で提出された λmax(M, Z) 式 を以下のように変更した。 λmax(M) = λmax(M + ΔM λ) ここに、ΔMλ = 200(0.004 - Z) Mo である。 左辺はλmax(M)This Paper とすべきだろう。 この補正項は第3ドレッジアップは低メタルほど有効になるという理論的予測 と合致する。そして、それは SMC における炭素星光度関数の暗い方のウイングを 再現するのに必要である。そこは Z ≈ 0.001 にまで至る低メタルの小 質量炭素星が占めている。 Nr の表現 Karakas02 に議論されている通り、Nr を M と Z の関数として表わす簡単な 規則は存在しない。かなり満足のいく表式は以下のようである。 Nr = a1 + a2 [ a3 - exp( a4M1IP )] ×[ a5 + a6exp( a7 - M1IP ) 2] (6) 2.5.3.シェル間物質の組成シェル間領域の4He, 12C, 16O の量は コアマス成長 ΔMC = MC - MC, 1TP の 関数として Boothroyd,Sackmann 1988 に 述べられている。彼らの図9をフィットすると、ΔMC ≤ 0.025 Mo では、 X(4He) = 0.95 + 400(ΔMC)2 - 20.0ΔMC |
X(12C) = 0.03 - 352(ΔMC)2
+ 17.6ΔMC X(16O) = -32(ΔMC)2 + 1.6ΔMC ΔMC > 0.025 Mo では、 X(4He) = 0.70 + 0.65(ΔMC-0.025) X(12C) = 0.25 - 0.65(ΔMC-0.025) X(12C) = 0.02 - 0.065(ΔMC-0.025) この関係式は図9に示される。これを見るとX(12C)が急激に上昇して MC = 0.025 Mo で最大値 0.25 に達することが判る。同様に、X(16O) もMC = 0.025 Mo で最大値 0.02 に達する。しかし、X(4He) は鏡像の関係にあり、そこで最小値 0.70 となる。 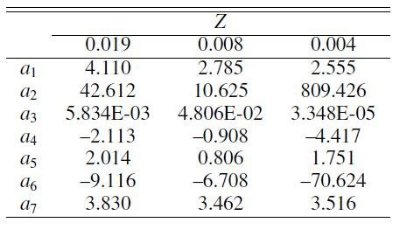 表2.式(6) の係数。 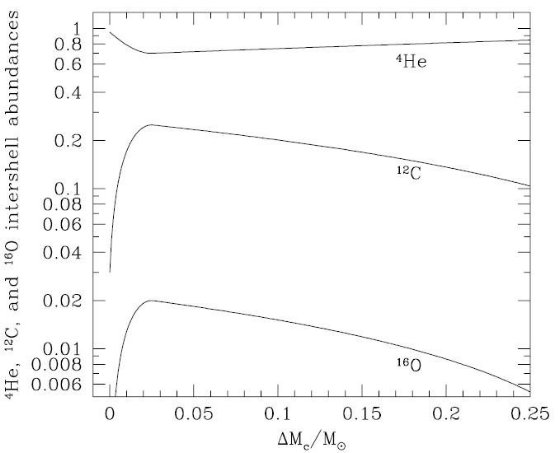 図9.ドレッジアップされるシェル間物質の化学組成。 |
2.6.ホットボトムバーニング (HBB) による核合成ホットボトムバーニングの影響HBB は Mi > 3.5 - 4.5 Mo (Z に依る) の TP-AGB で見られる。それは 対流層の深部に起こる CNO サイクルである。本論文では Marigo et al 1999 の 扱いに従う。 観測の観点からは、HBB は Mc - L 関係よりも星を明るくするばかりか、表面 組成に大きな変化をもたらす。中で最もよく知られているのは、CをNに転換する 作用である。その結果、炭素星の誕生は遅れさせられ、場合によっては阻止される。 しかし、場合によっては N に味方して O を破壊することにより、炭素星の形成 を助けることもある。この作用は低メタル高質量の星で働き、対流層基部の温度が 高いために ON サイクルが働くのである。 HBB 計算の合成 TP-AGB モデルへの組み込み ここで強調しておきたいのは、間パルス期の各タイムステップ毎に HBB を伴う TP-AGB モデルでは外層の化学組成が核反応ネットを用いて計算し直されている ことである。その結果、この合成 TP-AGB モデルでは、HBB 核合成の結果が 構造進化と矛盾なく組み合わされ、TP-AGB の完全モデルに非常に近いものに なっている点である。実際、Izzard04 で示されたようにパラメタ―方式で HBB 核合成を扱うと極めて複雑で困難なものになるのである。 それに反し、我々の外層積分方式は例えば対流層基部の温度 Tbce を自然に与える。 Tbce の進化を Mi = 4 Mo, Z = 0.008 の場合につ いて図10に示した。カーブの上辺は静謐期を表わしているが、徐々に最大値 へと近づき、大規模マスロスが開始されると急激に落下することが判る。 |
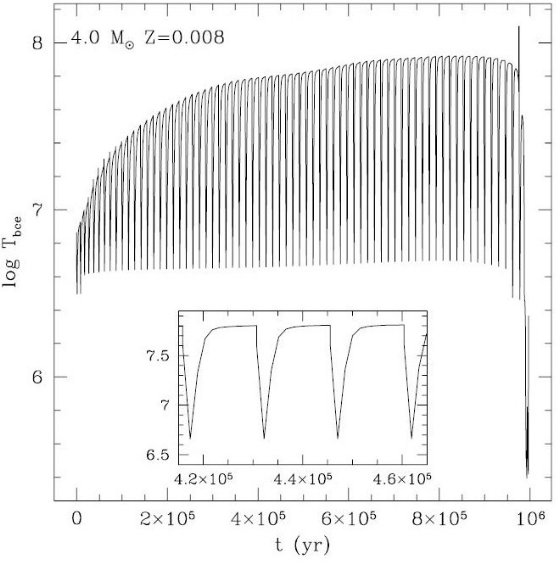 図10.対流層基部の温度 Tbce の進化。 Mi = 4 Mo, Z = 0.008。 第3ドレッジアップと HBB の双方が起きている。窓は拡大図。 |
2.7.脈動モードと周期脈動成長率 GR と光度 L脈動 AGB 星のモデル(Fox, Wood 1982)は各脈動モードの間でどれが支配的 かを決める成長率の大きさは光度に関係することを示唆する。高次の振動ほど 低光度で成長率が大きい。これは、基本振動( FM ) の成長率 GR0 と 第1倍振動( FO ) の成長率 GR1 で考えると、低光度では GR1 > GR0 を意味する。 従って、星が AGB を上がって行くと、支配的なモードが第3倍振動 ⇒ 第2倍振動 ⇒ 第1倍振動と変化して行き、最終的には基本振動になる のである。Lattanzio, Wood 2003 臨界光度 L1-0 高次振動の理論的データが欠けているので、本論文では第1倍音振動と基本振動 に話を限る。我々は AGB 星は第倍音振動で出発すると考える。基本振動への転換は 光度が一定値 L1-0 に達したときに起こる。そこで、 GR1 = GR0 となるのである。 L1-0 を得るため、Ostlie, Cox 1986 が計算したミラ型星の線形 非断熱振動の結果を利用しよう。彼らの結果をフィットすると、 log L1-0/Lo = -14.516 + 2.277 log M/Mo + 5.046 log Teff (9) 図 11 から判るように、第1倍音振動から基本振動への転換は、高マスほど 高光度で起こる。Ostlie, Cox 1986 の計算は太陽組成 (Y=0.28, Z=0.02) に限ら れていた。Fox, Wood 1982 は Z = 0.001, 0.01, 0.02 の長周期変光星モデルを 計算したが、Bedijn 1988 はその結果に基づき、(9) 式に Z 依存性を加えた。 それによると、第1倍音振動から基本振動への転換半径 R1-0 は (Z/0.02)-0.042 で変化する。そこで、(9) 式は次のように変わる。 log L1-0/Lo = -14.516 + 2.277 log M/Mo + 5.046 log Teff - 0.084 log(Z/0.02) (10) 周期 Fox, Wood 1982 は振動周期に (P, M, R) 関係を導いた。特に第1倍音振動の 周期 P1 に対しては、脈動定数 Q の解析的フィットから、 Q/days = (P1/days)(M/Mo)1/2(R/Ro)-3/2 (11) = 0.038 (M>3Mo, または M=2Mo,P1<300d, または M=1Mo,P1<200d) = 0.038 + 2.5 × 10-5(P1 - 300) (M=2Mo,P1>300d) = 0.038 + 4.5 × 10-5(P1 - 150) (M=1Mo,P1>150d) = 0.038 + 5.5 × 10-5(P1 - 100) (M=0.7Mo,P1>100d) |
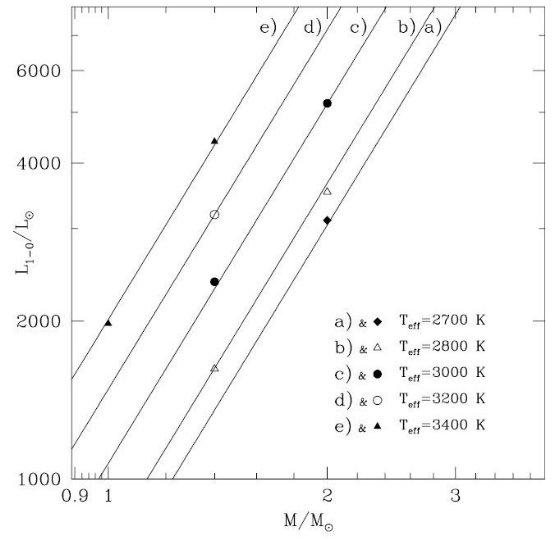 図11.FO と FM モードの成長率が等しいとして定義される臨界光度 L1-0 マークは色々な (M, Te) に対する Ostlie, Cox 1986 の脈動モデル。 実線 (a - e) は、式 (10) へのフィット。各線は異なる Te に対応。 本当かどうか、観測的には質量が判らないと。 一方、基本振動 P0 に関しては、 log P0 = -2.07 + 1.94 log(R/Ro) -0.9 log(M/Mo) (M<1.5Mo) (12) = -2.59 + 2.2 log(R/Ro) - 0.83 log (M/Mo) -0.08 log (Z/0.001) + 0.25 (Y - 0.3) (M>2.5Mo) これらの式は、Groenewegen,de Jong 1994 (M<1.5Mo), Fox,Wood 1982 (M>2.5Mo) から採った。1.5 < M/Mo < 2.5 に関しては両者の内挿で P0 を 求める。 |
2.7.1.注意:炭素星の脈動をどう扱うか?P - L 関係現在のところ、脈動モデルは酸素リッチな星に限られている。これは、 (P, M, R) 関係を炭素星に拡張することができないことを意味する。モデルが 頼れないので経験的なアプローチを試みる。例えば、式 (11), (12) を炭素星 モデルに適用すると、同じ光度 L ならば炭素星の方が大きな R を持ち、従って 長居 P になる。 既に Wood et al 1983 が注意したようにこの予想は観測と合致しない。と いうのは M-, C- 型星のどちらも同じ Mbol - P 関係に従っている からである。(Wood et al 1983 図 6 を見よ。) これは最近のより広範な サーベイ(Groenewegen 2004, Fraser et al 2005) によっても確認された。 Wood et al 1983 が示唆したように、上の事実が示すのは光球半径と違い脈動 AGB 星の慣性半径は C/O 比にあまり影響されないのだろう。他の言い方をすると、 炭素星の光球半径がオパシティ効果で膨らんでも慣性半径は変化しなかったのだ。 慣性半径 これらの理由で、我々は慣性半径 R を単純に次のように決めた。 R = L0.5Te2 (M-型星) (13) R = L0.5TeM2 (C-型星) (14) 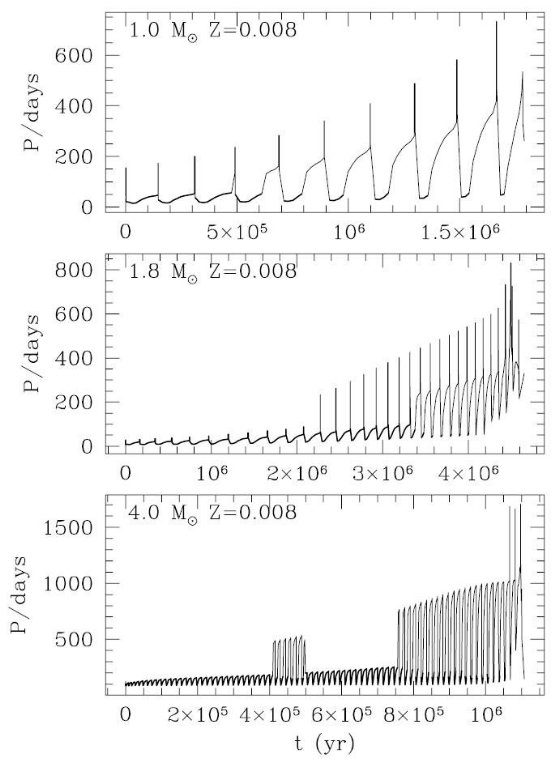 表12.Z = 0.008 TP-AGB モデルの脈動周期。細線= P0 太線= P1 | この R は M-型星の場合は光球半径と一致する。炭素星の場合、同じ光度 L を持つ M-型星の有効温度 TeM を使って求められる。この、 TeM は 仮想的な O-リッチ組成の大気を積分して決められる。 第1倍音振動と基本振動の切り替えへの影響 こうして決められた PT-AGB の周期変化を図12,13に示した。熱パルスに 伴う光度と光球半径の変化は周期 P の準周期的変動として示されている。それは 詳細な AGB モデルとその脈動周期の結果と一致する。(Vassiliadis, Wood 1993, Wagenhuber, Tuchman 1996) その上、図を見ると第1倍音振動と基本振動との間 の切り替えが周期のファクター2の変化としてはっきり現れている。式(10)のモード 転換の基準光度によれば、モード転換は TP-AGB 期に一度起きるだけの現象では なく、熱パルスに伴う光度変化の結果、数回起きると考えられる。 図12,13で判るが、熱パルスによる光度落下期は第1倍音振動、光度が回復 していく静謐期は基本振動によって占められる。式 (10) で L1-0 に 対する Teff 効果が表現されているが、その結果低温では基本振動が有利になる。 これがはっきり現れているのが図12下段の Mi = 4, Z = 0.008, t≈ 5 × 105 yr 付近で一時的に基本振動が出現した現象で、これは第3ドレ ッジアップが HBB に勝って短期間炭素星になった時 Te が低下したための効果で ある。 これはLMCの観測にはでないだろうな。 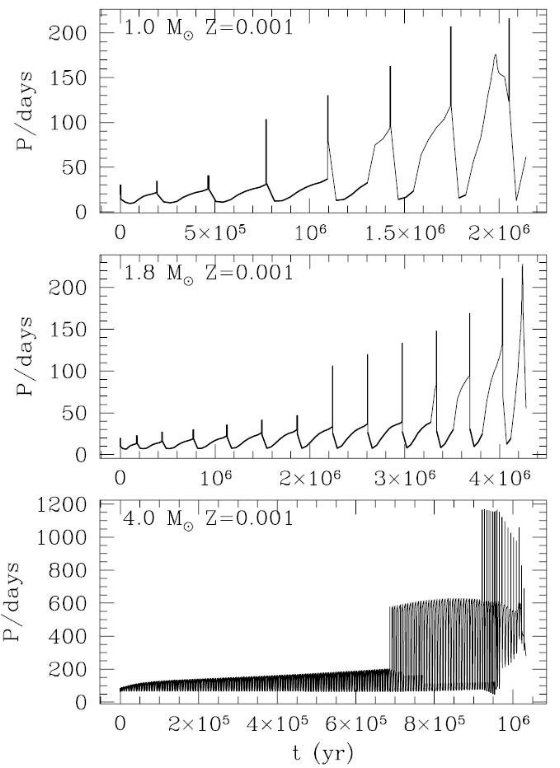 図13.Z = 0.001 の周期進化。 |
2.8.1.O-リッチモデルBowen,Wilson のマスロス式.O-リッチ星に対してはダストを含んだ動力学モデル (Bowen,Wilson 1991) の 結果を用いる。太陽組成のミラ型星モデル大気グリッドが Mi = 0.7 - 2.4 Mo, P = 150 - 800 d の範囲で計算されている。脈動は基本モードを仮定している。 彼らは以下の関係を導いた:
これは、図14のキャプションに書いたように dlog L/dt =2.45 × 10-7 [yr-1] と同じ。 O-リッチ星質量放出率の進化 (M, Po)を与えた O-リッチ星の質量放出率は以下の手続きで決まる。 (0)Ostlie, Cox 1986 の Po - M - R 関係から、R が決まる。 (1)M, R, P(2.7節)から、Bowen,Wilson 1991 式(3)で L が決まる。 ほんとは Iben 1984 の M - R - L 関係。 しかし、この二つから P - L 関係が出るな。 (2)以上のセットに対し、動力学モデルから (dM/dt) が求まり、 Mc - L 関係から (dL/dt) が決まるから、(dlogM/dlogL) が決まる。 (3)最後に、上の式から dM/dt が決まる。 (2)で (dM/dt) は決まるので (3)は変。 図14は TP-AGB 進化経路のグリッドを示す。 (この図は Bowen, Willson 1991 の図2と同じ。) 図で進化経路が急に落下する点が 超星風の発生点である。大体 dlogM/dlogL ∼ -1 と考えると -(dM/dt) = 5.67 × 10-7 × M Mo/yr に相当する。 Bowen,Willson 1991, Willson 2000 に論じられた通り、低メタルになると次の 二つの効果が現れる。それらは、 (a) 形成ダスト量が少ない。 (b) 同じ L では R が小さい。 後者の効果の方が大きいことが判った。その結果、図14の落下点が明るい L へとシフトする。Bowen,Wilson 1991 によると、Z < 0.1 Zo では超星風の発生は 次の臨界光度 LSW で起きる。 LSW(Z) = LSW(Zo) + [0.12 - 0.13 log(Z/Zo)] 幾つかのコメント (1)Bowen, Wilson 1991 は M - R - L, M - R - P, Mc - L など 独立の著者の AGB 静水モデル の結果を採用して AGB星構造を定めてから動力学 モデルを計算している。それらは我々の合成進化モデルで採用した式と一致しない 場合もある。例えば異なる Mc - L 関係など。にも拘らず、採用した方法は 現在のところ最良の方法である。その上、得られた結果は観測と以前よりはるかに よい一致を示す。 (2)Bowen,Wilson 1991 は基本振動に対して得られた結果で高次の振動に対する 計算はない。 しかし、大気の底をサイン関数で揺らすだけ だから、基本振動も第倍音も無いんじゃないのか? Bowen 1988 は幾つかのセットに対しダストの入った第1倍音振動の 計算を行った。基本振動と第一倍音振動での質量放出率の比較は図17に与えた。 基本振動と第一倍音振動による質量放出率の比は単調な変化は示さない。そこで、以下の ような式で近似した。
式 (18) 中の係数は表3に与えた。 実際には第一倍音の質量放出は以下のようにして求めた。 (1)M, R, L を与えた星の Po を式 (12) から計算する。 (2)2.8節に沿って (dM/dt)o を計算する。 (3)式 (18) を用いて、(dM/dt)1 を求める。 このやり方は Bowen 1989 が計算した数個の第一倍音振動モデルの結果に基づいており、 完全なものでないことは認識している。しかし、これは第一歩である。それに、単純に P = P1 ≈ Po/2.2 の基本振動に対する質量放出率へと変換するだけ よりも実際に近い。この変換法だと恐ろしく低い値しか出て来ない。ところが SR の ような短周期 AGB 星でもミラと同じくらい、数 10-7 Mo/yr に達する 質量放出を示す。(Oloffson et al 2002) もしそれらの星を第一倍音振動星とすると、 (i) (dM/dt) が P に対し振動モード毎に異なる依存性を持つか、(ii) 実は (dM/dt) が P に無関係に決まっていて、他のパラメターが効いているかであろう。第一倍音振動 モデルの動力学的モデルの解析は非常に重要である。 |
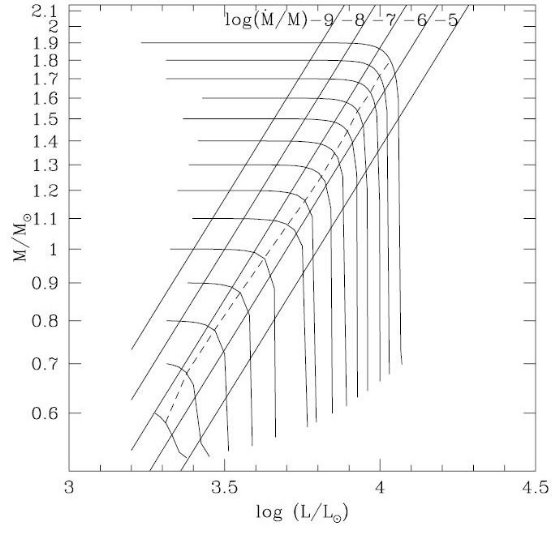 図14.Z = 0.019, O-リッチ TP-AGB 星の質量変化。質量放出率は Bowen, Wilson 1991 のミラ型星動力学モデルに基づいて決定した。 実線5本は (dM/dt)/M = 10-9 (/yr) - 10-5 (/yr) のラインで、 夫々が各Mi毎の進化曲線の勾配 dlog M / dlog L = -0.0018, -0.018, -0.18, -1.8, -18 に対応している。 dln M/dt=10-9/yr が dlogM/dlogL=-0.0018 に対応するということは、 dlnL/dt = (1/1.8)10-6/yrを含む。 鎖線は崖縁を結ぶ、dlogM/dlogL=-1 または、dlnM/dt = 5.6710-7 (/yr) のラインである。 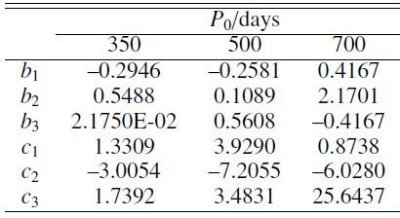 表3.式 (18) 中の係数 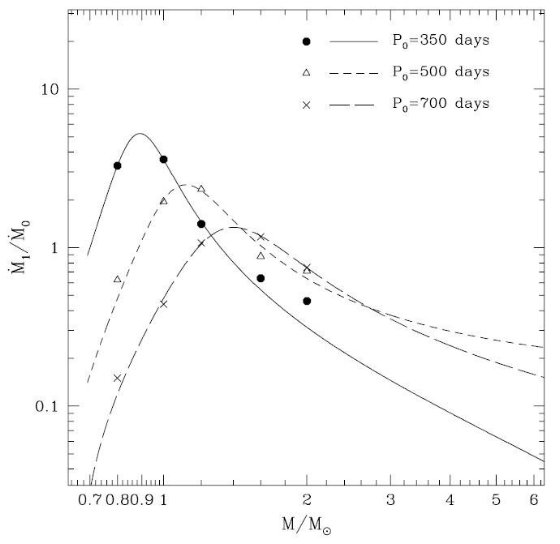 図17.第1倍音振動と基本振動による放出率の比 |
2.8.2.炭素星の質量放出炭素星の星風モデル炭素星の星風モデルはベルリングループが展開した。Fleisher et al 1992, Sedlmayr,Winters 1997, Winters et al 2000, Wachter et al 2002, Winters et al 2003. 炭素星モデルグリッドに対する質量放出率が Te = 2200 - 3000 K, L = 3000 - 24,000 Lo, M = 0.8 - 1.8 Mo, C/O = 1.20 - 1.80, P = 100 - 1000 d で得られて いる。Wintersw et al. 2000, 2003 の詳しい解析によると、星風に関して二つの はっきり異なる領域がある。 B-型星風 第1領域は B - 型モデルと呼ばれ、低光度、短周期、高温度巨星である。これら の星では脈動により星風が駆動される。ダストへの輻射圧の効果は小さい。 実際、α ≡ (arad/agrav) < 1 なので、 輻射圧だけでは外向きの流れを作り出せない。v < 5 km/s の低放出率流が 形成されるが、臨界光度の -(dM/dt)crit ∼ 3 × 10-7 Mo/yr を越えることは無い。 A-型星風 -(dM/dt)crit を超えるためには光度が LSW 以上となり α > 1 となる必要がある。Winters et al 2000 モデルによると、この LSW は星の質量と有効温度による。 L ≥ LSW となると、 炭素星はダスト駆動の A-型星風領域に入る。そこでは、3 × 10-7 ≤ -(dM/dt) ≤ 10-4 M/yr となる。そして 5 < v < 40 km/s である。 臨界光度 これらを念頭におきTP-AGB 炭素星からの質量放出を次のように求める。 (A) LSW を定める。 LSW 式の拡張 Schroder et al 1999 の星風計算に基づき、 Schroder et al 2003 は M と Teff の関数として LSW を与えた; log (LSW / Lo) = 3.8 + 4( log Teff - 3.45) + log ( M/Mo ) (19) この関係は P = 400 d, C/O = 1.3 に固定し、 M, Teff を変えた比較的少数の モデルの結果から導かれた。 この論文では、上の式に周期依存性を組み込んだ。そのため、M. Teff, P, C/O, Δv (ピストン速度) を変化させた Winters et al 2000 の脈動星風モデルを 用いた。C/O = 1.2, Δv = 5 km/s に固定した結果は: log(LSW / Lo) = 3.796 + 6.614 log (Teff/2800K) + 1.096 log (M/Mo) - 1.728 log (P/400d) (20) 比較のため図18には LSW を Teff = 2800 K の場合につき、式19 と 20 で示した。新しい式(20) が式(19) を再現していることが判る。また、式(20) の結果は 周期が長いと低光度で超星風が発生しやすいことも判る。 L < LSW の星風 L < LSW の場合には質量放出率は赤外カラー J-K の関数として次の ように半経験的に表わされる。Schroder et al 2003.
この式は Le Bertre 1997 による、穏やかな質量放出をする銀河系炭素星, |
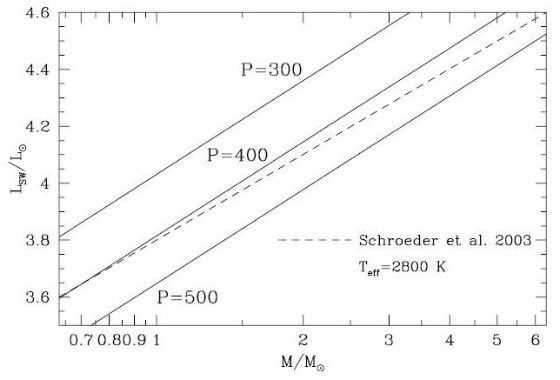 図18.炭素星超星風発生のための Teff = 2800 K における臨界光度。 破線: P = 400 d (式19), 実線:式20 P=300, 400, 500 d 2.5 ≤ J-K ≤ 4, の質量放出率にフィットしたものである。ここで用いられている J - K カラーは Marigo et al 2003 が提案した関係、 J - K = 17.32 - 4.56 log Teff + 0.052(C/O) (22) から決められた。この式は、Bergeat et al 2003 のカラー対Teff 関係を (C/O) 効果 を入れて拡張したものである。 (B) LSW を超えた星風。 ダスト駆動の超星風 炭素星の L > LSW になると、ダスト駆動の超星風が発生する。この 時期の脈動星風のモデルは Wachter et al 2002 が調べた。彼のモデルでは星風の駆動 はダストに働く輻射圧が原因である。彼らのモデルをフィットして、 log [-dM/dt(Mo/yr)] = -4.529 - 6.849 log(Teff/2600K) + 1.527 log (L/104Lo) - 1.997 log (M/Mo) - 0.995 log (P/650 d) + 0.672 log [(C/O)/1.5] (23) 式の係数は Wachter et al 2002 の式(1) と非常に近い。違うところは式(23) では (C/O) 依存性が表現されているところである。この項を入れた理由は銀河系炭素星では (C/O) の効果は小さいが低メタルの炭素星では C/O 効果が大きくなるからである。 低メタルだと C/O が大きくなっても [C/H] はそう大きくない。 それより、上の式には Z 依存が入っていない。 炭素星質量放出のまとめ 計算された質量放出率の例を図15,16に示す。どの場合も C/O に関係なく 以下の点が目につく。 (i) 質量放出率は、熱パルスが原因の光度と有効温度変化により変動する。 (ii) 質量欠損は熱パルス前の光度が高い静謐期に起きる。 (iii) 超星風は基本振動期に起きる。 |
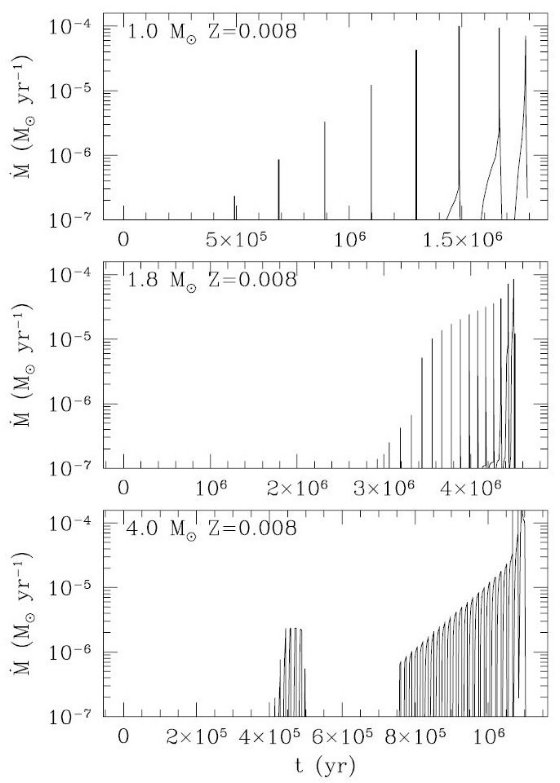 図15.Z = 0.008 の星の質量放出率変化 炭素星がどこかは記述なし。 |
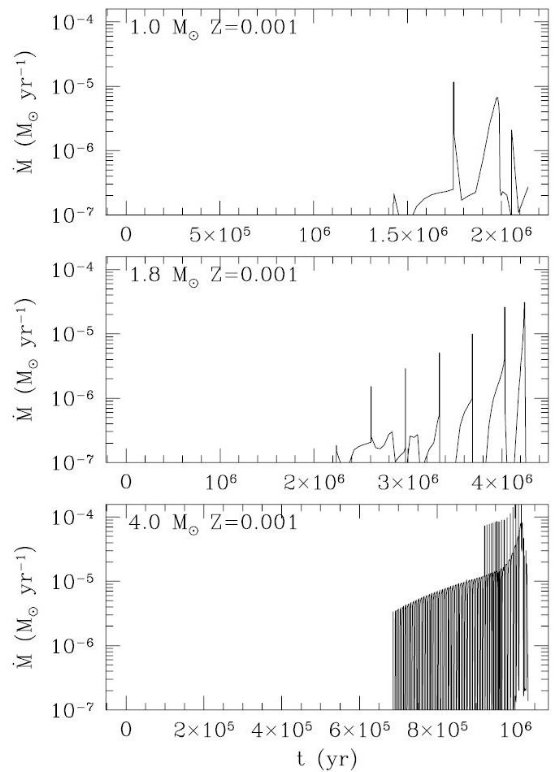 図16. Z = 0.001 の星の質量放出率変化 炭素星がどこかは記述なし。 |
|
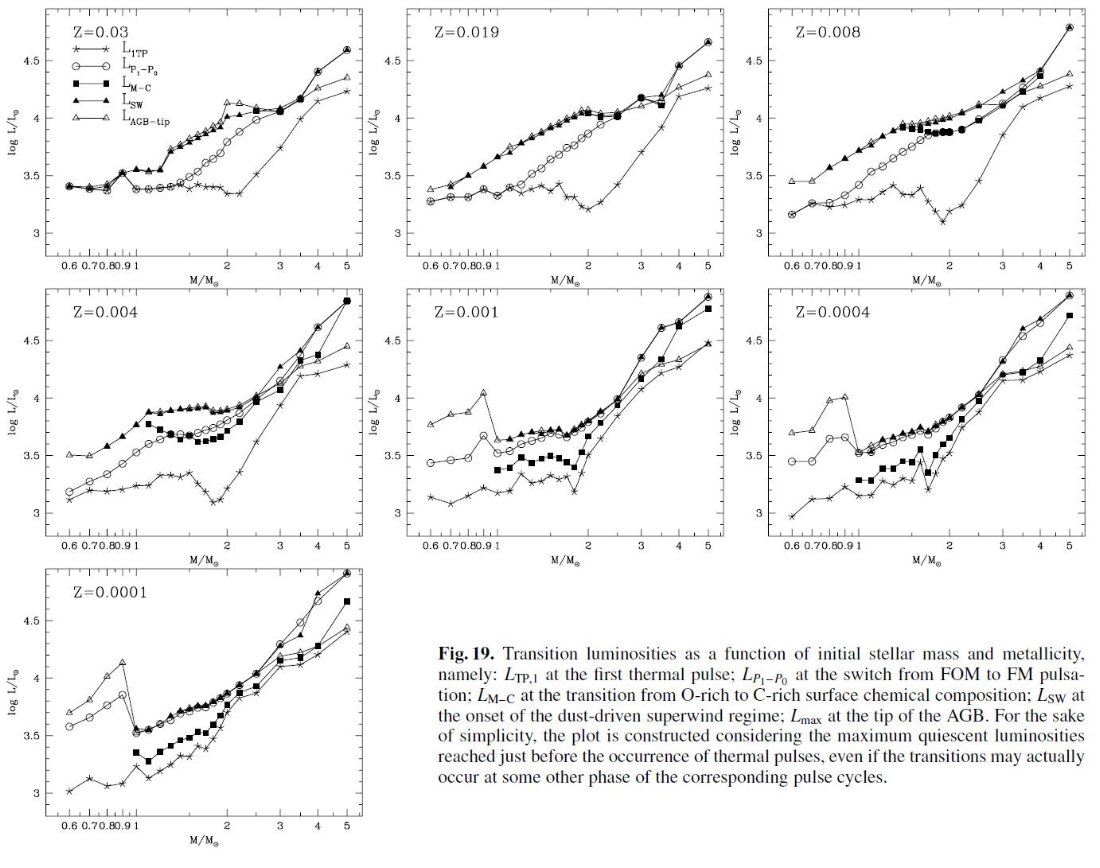
今回のモデルの改良点 第2章で述べた合成 TP-AGB モデルは、M = 0.5 - 5.0 Mo, Z = 0.0001, 0.0004, 0.001, 0.004, 0.008, 0.019, 0.03 のセットについて、進化が計算された。計算は 最初の熱パルスから外層が完全に吹き飛ぶまで追跡された。 次の節からは、 TP-AGB 進化モデルの基本的な性質を述べる。重要な点は、 (i) 変更周期に第1倍音振動から基本周期への転換を導入した。 (ii) 質量放出率の計算を O-リッチと C-リッチで分けた。 (iii) 組成変化に即したオパシティの計算。 (iv) 第3ドレッジアップと HBB をより詳細に扱った。 3.1.転換光度5種転換光度の定義図19には次の種類の転換光度を、Z = 0.0001, 0.0004, 0.001, 0.004, 0.008, 0.019, 0.03 のセットについて Mi の関数として示した: LTP,1 = 第1熱パルス、L1-0 = 第1倍音から基本振動、LM-C = O-リッチからC-リッチへ、LSW = ダスト駆動超星風。 Lmax = AGB 先端 図19を見ると以下のようなことが判る。 LM-C :炭素星 LM-C は Z の低下とともに下がる。その上、炭素星になるための最小質量 も、 Z の低下とともに下がる。例えば、Z = 0.019 では M ≥ 2.0 Mo だが、 Z ≤ 0.001 では 0.8 Mo である。球状星団が引っかからないか? |
L1-0 :基本振動 L1-0 は Z の低下とともに上昇する。Z = 0.019, 0.030 で M ≤ 1 - 1.5 Mo の場合のみ、第1熱パルス発生時に基本振動をしている。それ以外の場合、つまり Z =0.008, ..., 0.0001 では全ての星で、Z = 0.019, 0.030 でも M > 1.5 Mo では 第1熱パルス発生時に第1倍音振動で、その後基本振動に移る。 炭素星の振動モード L1-0 と LM-C を較べると、低メタルではどの質量でも 炭素星は初め第1倍音で振動し、ある光度で基本振動に移る。メタル量が上がると LM-C も上がり、炭素星は初めから基本振動を持つようになる。 超星風 超星風が起きるのは、炭素星でも O-リッチ星でも基本振動になってからである。 そして、その時の光度が実際には AGB 先端光度を決める。 炭素星の超星風 Z ≥ 0.019 の高メタル星では、炭素星転換に伴う Teff 低下が超星風の発生を 引き起こす。したがって、 LM-C &asynp; LSW である。低 メタルになると、炭素星転換に伴う Teff 低下が小さくなる。このため、超星風は L がより高くなるまで遅れる。 O-リッチ星の超星風 O-リッチ星では、Z が下がると Teff が上がるため、 LSW が高くなる。 低メタルの、例えば Z ≤ 0.001 では、Mi ≤ 0.8 Mo の星では超星風の最低条件 -(dM/dt) ≈ 5 × 10-7 Mo/yr に達しない。この様な場合、 AGB 期の終端はコアマスの成長で決まる。 |
Z = 0.030 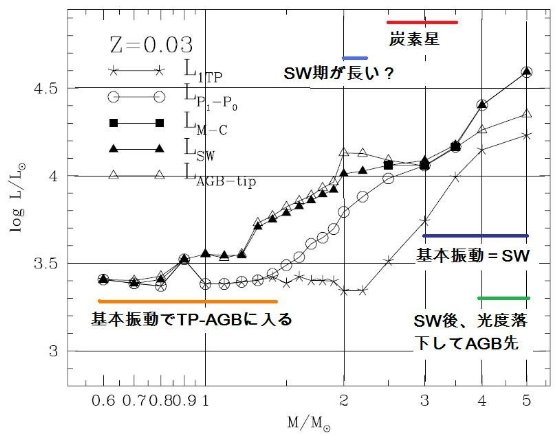 |
Z = 0.030 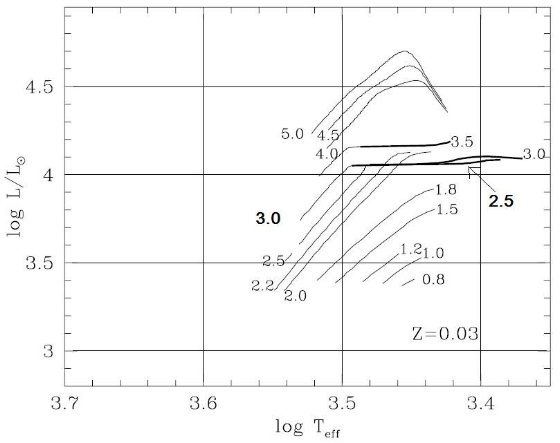 |
Z = 0.019 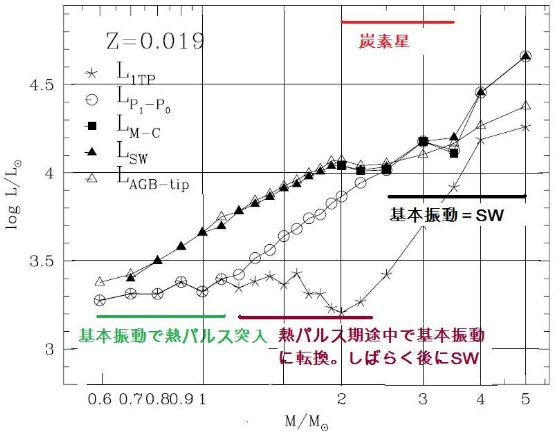 |
Z = 0.019 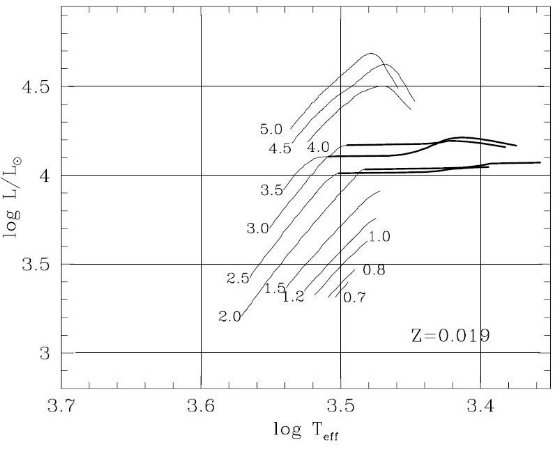 |
Z = 0.008 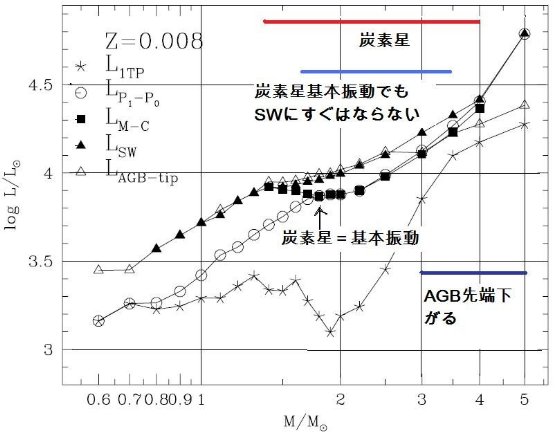 |
Z = 0.008 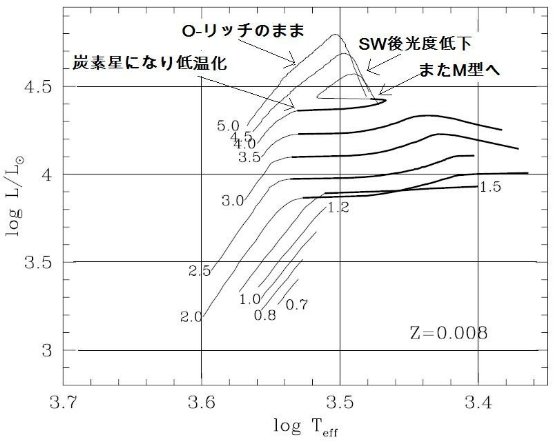 |
Z = 0.004 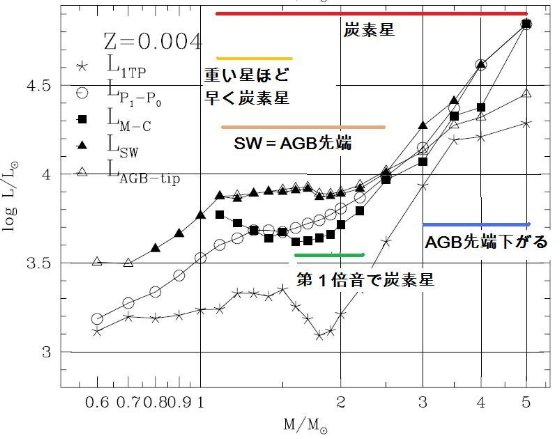 |
Z = 0.004 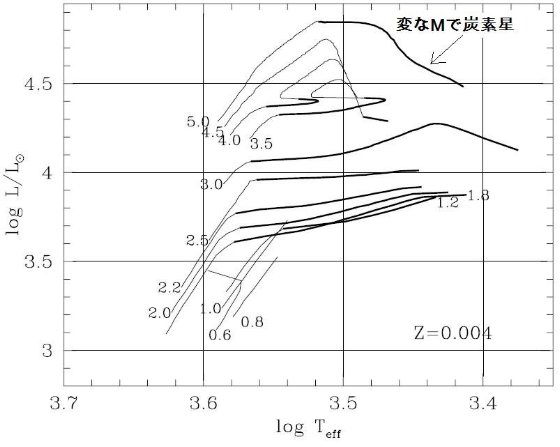 |
Z = 0.001 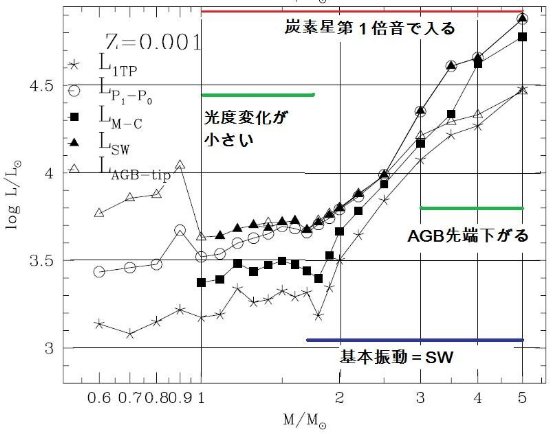 |
Z = 0.001 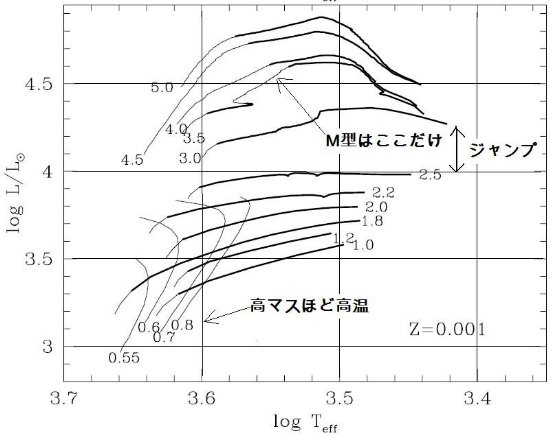 |
Z = 0.0004 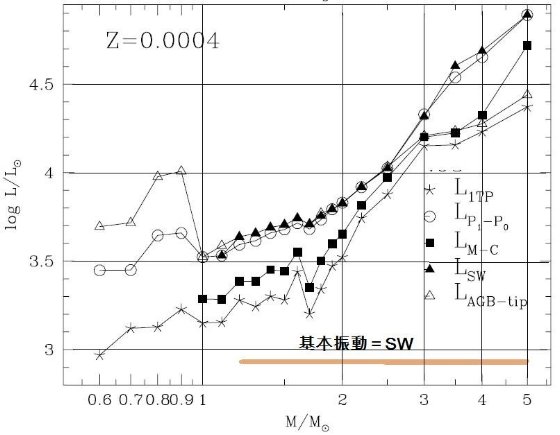 |
Z = 0.0004 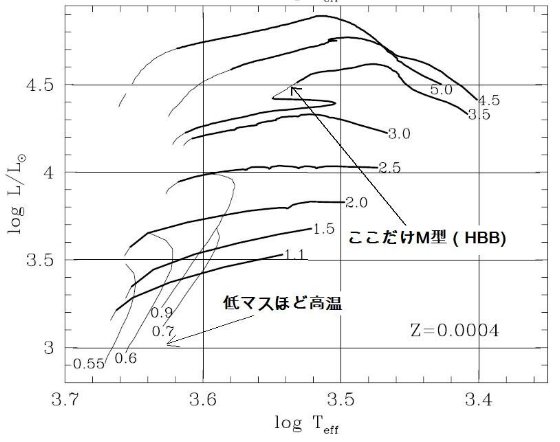 |
Z = 0.0001 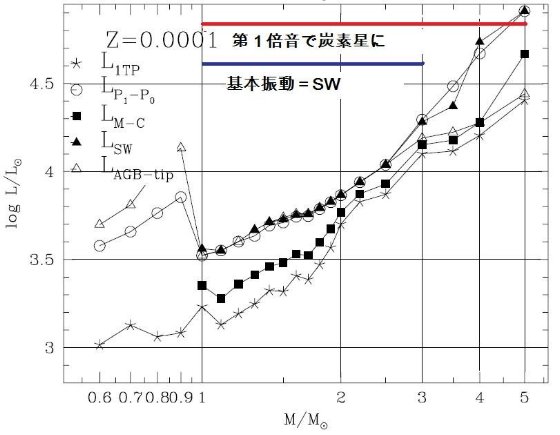 |
Z = 0.0001 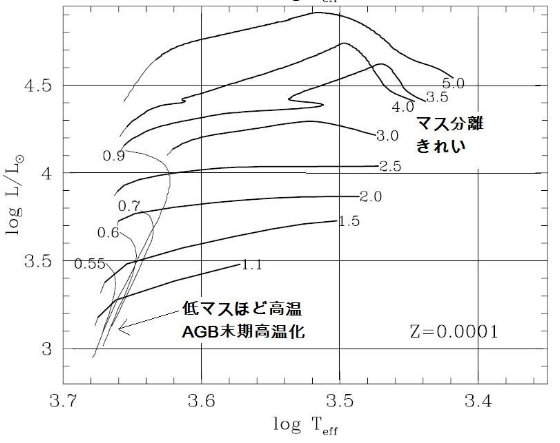 |
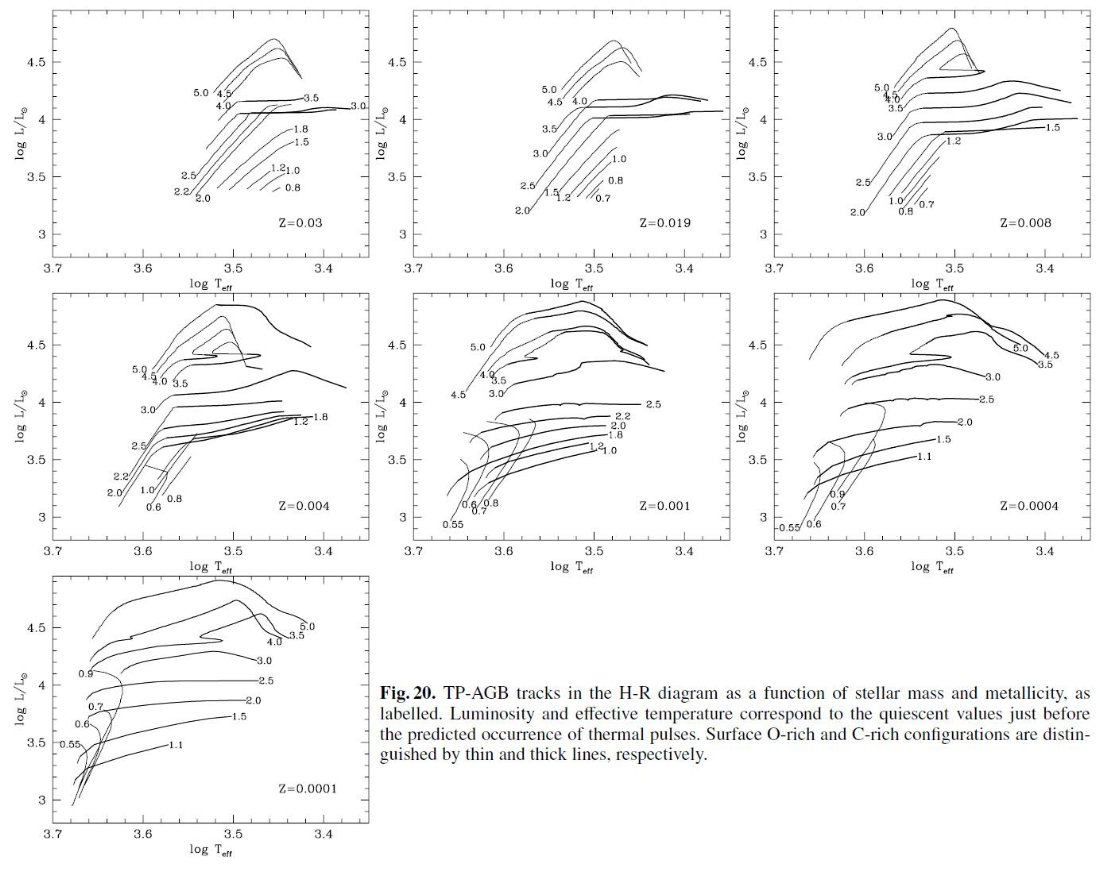
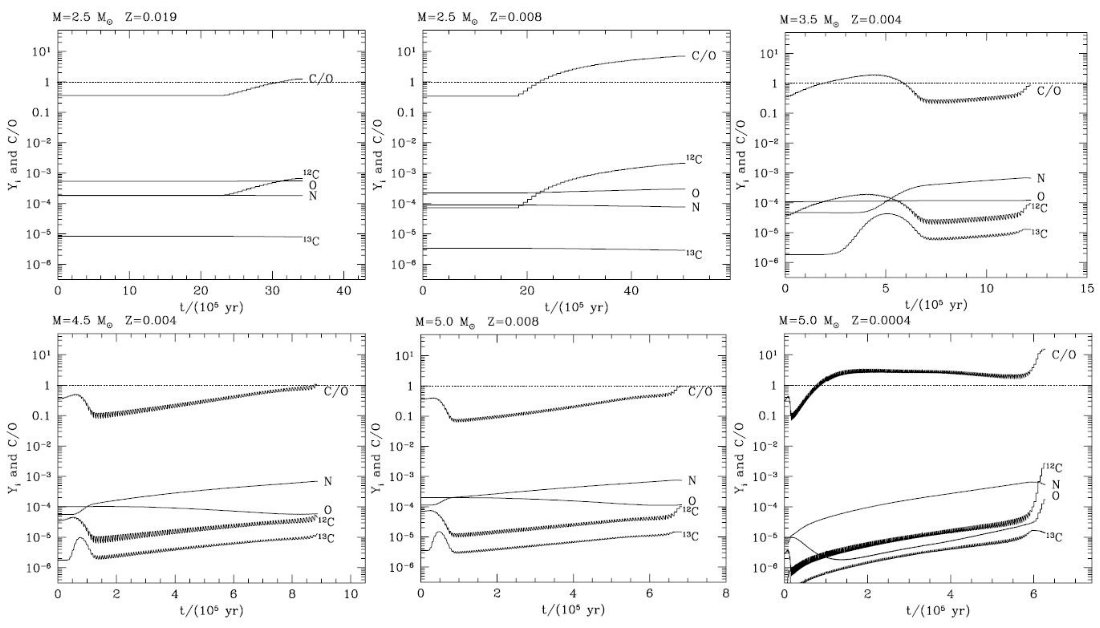
3.2.TP-AGB 進化経路TP-AGB 進化経路図20は HR 図上の TP-AGB の複雑な進化経路を Mi, Z 毎に示す。低質量で O-リッチであり続ける星の経路は、光度が上がるにつれ有効温度が緩やかに下 がることで特性付けられる。この傾向は C-リッチになると大きく変わる。図 の太線が低温側に伸びることから判るように、炭素星では分子オパシティが強まる 結果、大気が膨張して温度が下がる。この効果は低メタル星ほど大きい。これは 低メタルでは TP-AGB 初期のまだ高温の時期に炭素星化するためである。 HBB による再O-リッチ星化 一つ注意しておくが、HBB のために炭素星が O-リッチに戻る場合がある。例えば、 (Z = 0.008, M = 4 Mo), (Z = 0.004, M = 3.5 Mo) のケースがそれであ |
る。図 20
ではそれらは HR 図上のジグザグコースとしてはっきり示されている。 HBB-II M > 4 Mo, Z > 0.004 では HBB 効果のため、C/O < 1 に抑えられて しまう。しかし、低メタル Z ≤ 0.001 になるとこの HBB 効果で炭素星化を防 ぐことは出来ない。対流層基部で ON-サイクルにより O が N に変換される。 HBB-III 質量が大きい星では HBB による光度超過が目立つ。図20でも、進化経路を見ると Mc - L 関係を上まわって光度が上昇している。その時、ドレッジアップのため Mc は それほど大きくない。しかし、SW が開始され外層質量が減ると HBB が消え、光度は 元の Mc - L 関係の値へと戻るのである。 |
3.3.表面組成の進化ドレッジアップのみの場合第3ドレッジアップのみを経験する星では12C が段々と増加して行く。 そして、C/O > 1 となった時に炭素星が出現する。 図21の M = 2.5 Mo のケースがそれに相当する。 Z = 0.008 の炭素星の期間は Z = 0.019 の時よりずっと長い。N, O 組成には大きな変化は起きない。 第3ドレッジアップ + HBB の場合 進化の様子はドレッジアップと HBB との比率による。以下に各場合を説明する。 1).HBB が途中で弱くなる場合。 もし初めに第3ドレッジアップが支配的であるならば、C/O 比が上昇し、炭素 星領域に入る。その後 HBB が強くなると、C が N に変換され、再び C/O 比は1以下とな る。このケースが当てはまるのは、質量が中間値の 3.5 Mo で、Z = 0.004 の時である。 これらのモデルの進化は、分子オパシティの値と質量放出率に強く影響される。例えば Marigo 2007 が示したように、Teff 依存性の強い Vassiliadis,Wood |
の質量放出式を
組成変化オパシティと組み合わせると、 C/O > 1 になった直後に HBB が弱くなったり、
場合によっては停止したりする。そのような時には C/O の低下が止まり、AGB 終末まで
炭素星のままであり続ける。さらに詳細な研究が望まれる。 2).HBB が 12C を燃やしてしまう場合 高質量で HBB が新しくドレッジアップされてきた 12C を燃やしてしまう くらい強いと、炭素星への早期転換が阻止される。この様なモデルでは TP-AGB 全期 間中、最末期に SW のため HBB が停止し第3ドレッジアップがダストシェルに囲まれた 内部の星を炭素星に変えるまで、C/O が 1 以下に保たれる。(van Loon et al 1997, Frost et al 1998) その例が、図21の (Mi = 4.5 Mo, Z = 0.004), (Mi = 5.0 Mo, Z = 0.008) のケースである。 3).高温 HBB の場合 メタル量がうんと低い高質量星では HBB が炭素星形成の助けになることがある。 対流層基部の温度が ≥ 7.9 times; 107 K になり、ON-サイクルが 働いて O から N への変換が進む。この場合は C の増加でなく、 O の減少により O/C が 1 を超すのである。例としては、(Mi ≥ 4.0 Mo, Z ≤ 0.001), Ventura et al 2002 も似た結論を出している、で、図21の下段に示す。図を 見ると、初め C が減少し、CN サイクルの平衡値に達する。しばらく C の微増が 続き、その後 ON サイクルが開始されて O が激減する。ON サイクルの平衡値では O が C より少ないままである。 |
|
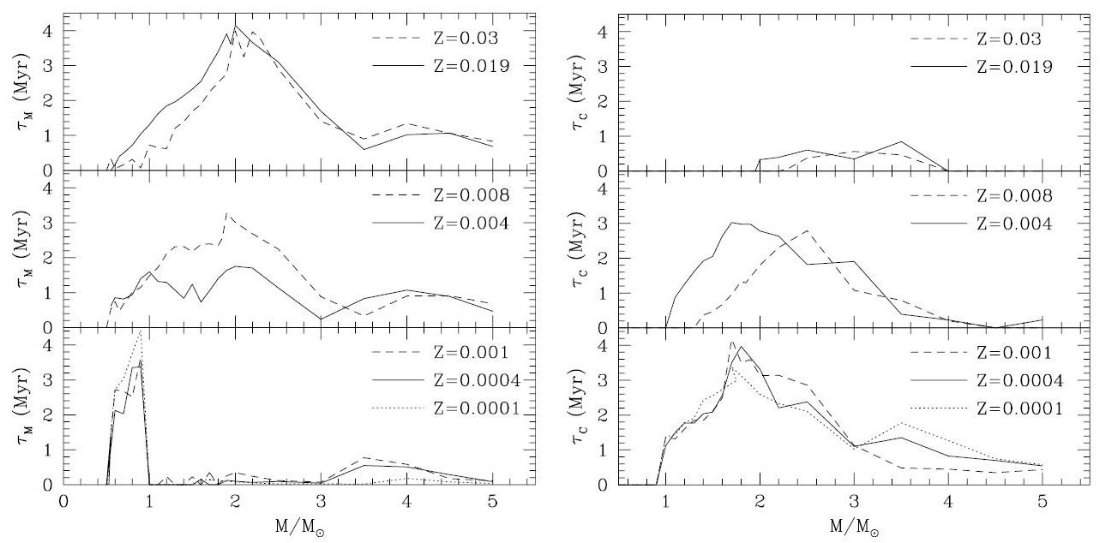
TP-AGB 期の終末 図22には TP-AGB 期の M-型星寿命 τM と C-型星寿命 τC を、log(L/Lo) ≥ 3.33 (Mbol ≤ -3,6) について示して いる。この結果は第4章に述べる較正に基づいている。その上、この寿命には TP-AGB 期最後の SW 期の効果も入っている。 TP-AGB 期は外層が失われた時点で終わる。明らかにその主原因は質量放出である が、コアマスの増大も寄与する。強調しておきたいのは、Z ≤ 0.004, M ≤ 0.7 Mo では SW が起きないので、コアマスが増加するまで AGB 期が続く。 M-型星寿命 τM より高質量では第3ドレッジアップが働き、これが M-型星寿命を定めている。質量 放出率の取り方は M-型星寿命には影響しない。 τM はドレッジアップ の二つのパラメター λ と Mcmin で決まる。 一般的には、低メタルになるとドレッジアップが早く始まり、効率も高いため、 |
τM が短くなる。興味深いのは、Z ≥ 0.008 では τ
M(Mi) が Mi ≈ 1.9 - 2.2 Mo 付近でピークを形成することである。
この現象の少なくとも一部は、第1熱パルス発生のコアマス MC,1TP(M)
がこの付近で極小値をとることと関係する。
その結果、Mcmin に辿りつく
まで長い時間がかかるようになったのである。4.2.節で論じるが、このピークは
LMC星団の M-型星カウントの結果とも合致する。 しかし、それは、他の Mi では TP-AGB以前の M-型期が長い ことを意味するのではないか?観測的には TP-AGB だけを選びだせないが。 C-型星寿命 τC 図22を見ると、メタル量と寿命の関係は C-型星では M-型星と逆になることが 判る。つまり、低メタルほど炭素星の寿命が長いのである。 Mi = 2.5 Mo で較べると、 0.6 Myr(Z=0.019) から 2.8 Myr(Z=0.008) へと延びるのである。しかし、非常に 低メタルになるとほぼ一定値 τC ∼ 2.4 Myr に落ち着く。これは、 質量放出とドレッジアップのメタル量依存性の結果である。 |
|
O-リッチミラ 今回のモデルが以前と異なるのは、理論的な質量放出率を入れた点である。図23は 周期 - 質量放出率関係を Z = 0.019 モデルと銀河系 M-型星とで較べたものである。 モデルが観測点の分布範囲をうまくカバーしていることが判る。特に与えられた周期に 対して質量放出率にばらつきがあることがこのモデルで上手く説明される点は重要で ある。Vassiliadis, Wood 1993 のように質量放出率を周期のみの関数として与えて いてはこの分散はうまく説明できなかった。その上、このモデルでは超星風の開始が 自然に予想され、幅広い周期に渡って OH/IR 星の存在が再現できた。 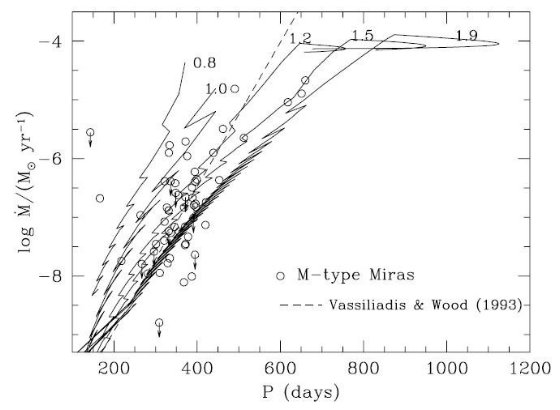 図23.O-リッチミラの質量放出率と周期の関係。 白丸=銀河系ミラ(LeBertre,Winters 1998, Groenewegen et al 1999) 破線=Vassiliadis,Wood 1993 半経験式。 実線=Bowen,Willson 1991 の Z = 0.019 星風モデル。 |
C-リッチミラ 似た結論が炭素星についても言える。図24を見るとさらにはっきりするが、モデルは -(dM/dt) ≈ 10-5 Mo/yr に見られるの平坦部(炭素星SW)を再現して いることは注目に値する。 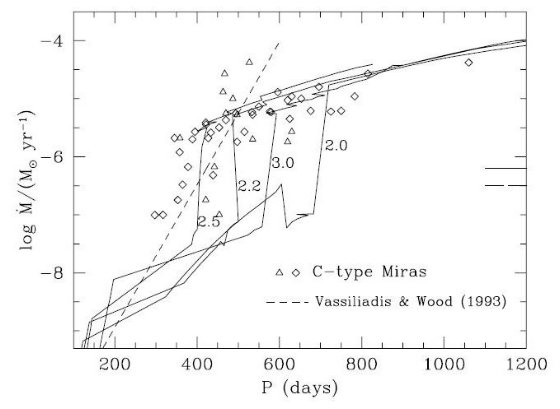 図24.C-リッチミラの質量放出率と周期の関係。銀河系炭素星の観測は、 ;四角=Groenewegen et al 1999、三角=Schoier,Olofsson 2001 破線=Vassiliadis,Wood 1993 半経験式。 実線=Wachter et al 2002 の Z = 0.019 星風モデル。 |
|
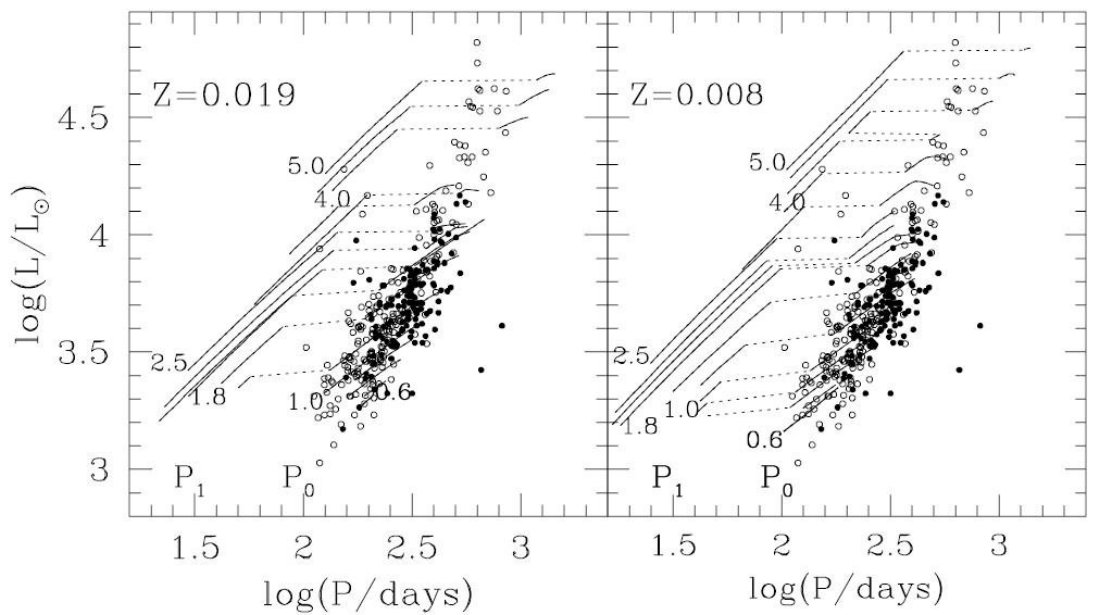
LMC ミラは基本振動 図25に示されるように、LMC ミラの広範な観測はこれらの星が明瞭な周期 - 光度関係に従うことを明らかにした。Feast et al 1998, Hughes,Wood 1990, MACHO survey. 図には観測点と重ね、幾つかの質量に対して Z = 0.019 と 0.008 の進化経路を描いた。2.7.節で述べた脈動モードの転換により、進化経路は P - L 面上で二つに分かれる。周期が短い方が第1倍音振動で、長い方が基本振動 である。明らかに、基本振動がミラの観測点と合致する。これは、ミラが基本振動 で脈動していることを意味する。 |
他の系列 他の脈動系列(Wood et al 1999)の詳しい解析はこの論文の範囲を越えている。 そのためには、TP-AGB モデルと脈動変光星モデルを組み合わせて、種族合成モデル を作る必要がある。 この作業は現在進行中である。 |
|
IFRM に影響するパラメターは数多い 高質量、低メタルでは第3ドレッジアップが盛んなので、単純には低メタルの IFMR は平坦になると期待される。しかしこれはそうではない。IFMR は第1熱パ ルスのコアマスを強く反映しており、低メタルではそれが大きいからである。 その上、低メタルでは HBB が有効で TP-AGB 期間が短く(?)コアマスを大きく 変える時間がない。したがって、 IFMR の実際の形は幾つかのパラメターに影響され、 簡単に推測できる性質のものではない。 観測とモデルの比較 図26は現在のモデルで予想した IFMR を連星系、散開星団中の白色矮星データ と較べたものである。星団年齢と白色矮星の母星質量は Girardi et al 2000 の 進化経路と等時線に基づいている。したがって、観測点とモデルの間にオーバー シューティングの取り扱いの違いによるずれは生じていない。図から以下の点が 注意される: 1).メタル量効果 モデル IFMR はメタル量に強く影響されている。その結果、ある初期質量に対し、 最終質量には 0.1 Mo の巾が付く。IFMR は低メタルほど急になる。一般には初期 質量が大きいほど最終質量も大きくなるが、Z = 0.03, M = 2.2 -3 Mo 領域の ように逆転する箇所もある。 2).観測的 IFMR データは広がりすぎていて、モデルのテストに使うのは難しそうに見える。しかし、 データ分散の原因は主に M 37 にあり、他の天体より系統的に高く出ている。 Dobbie et al 2006 にもコメントされている通り、M 37 の初期メタル量が確定 していないので今後値が変わる可能性がある。そこで、 M37 を除くと、 Mi > 2.5 Mo では IFMR が観測的によく定まることが判った。一方、 1.5 - 2.5 Mo では質の良いデータが得られていない。フィールド星は全て Mi < 1.5 Mo と仮定した。 これは乱暴すぎないか? 3)観測とモデルの比較 M 37 を比較から外すと、Z = 0.019 の M < 5 Mo モデルは観測点の分布と 非常によく合う。しかし、より大きな観測点が残っているので TP-AGB の計算は もう少し先まで伸ばす必要がある。 |
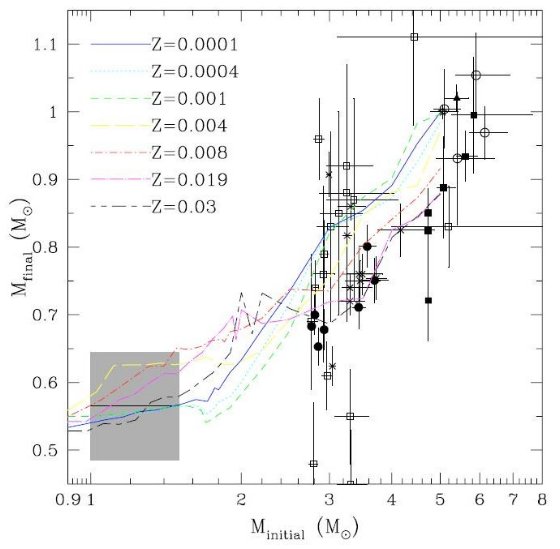 図26.モデル Mi - Mf 関係と WD 観測との比較。 黒丸=ヒアデス(Claver et al. 2001)、白四角= M 37 (Kalirai et al 2005) クロス=プレセペ(Claver et al 2001, Cobbie et al 2006) 黒四角= M 35 (Williams et al 2004)、星=シリウスB(Liebert et al 2005) 三角=プレアデス(Dobbie et al 2006), 白丸= NGC 2516 (Ferrario et al 2005) 灰色領域は Liebert et al 2005 によるフィールド WD の質量ピークと 1 σ 。 |
|
この論文で何が新しいか? 以前の TP-AGB モデル, Groenewegen, de Jong 1993, Marigo et al 1999 では パラメターの調整にマゼラン雲炭素星光度関数を使った。この論文では、炭素星と M-型星の寿命をそれに加えた。また、以前のモデルでは、LMC, SMC の星形成率が 過去一定であったとか、メタル量不変という簡単すぎる仮定を用いていた。この 論文では、他の研究で独立に得られた星形成史と年齢 - メタル関係を用いる。 4.1.マゼラン雲炭素星の光度関数(CSLF)LMC の観測 CSLFGroenewegen 2002 は局所群銀河の CSLF のまとめを述べている。彼が提供してく れた最新データファイルをこの論文では用いる。LMC の mbol はCosta, Frogel 1996 の 895 炭素星データを用いる。最も暗い炭素星で I = 15 で、観測限界は I = 17 なので、このサンプルは完全と考えられる。可視光探査から逃れたであろうダスト 炭素星の割合は Groenewegen, de Jong 1993 によれば Mbol < -6 で 3 % である。 測光等級から絶対等級への変換は Costa, Frogel 1996 が行い、平均エラーは 0.34 等である。mbol から Mbol への変換にはLMC で距離指数= 18.5 が用いられた。 得られた CSLF は Mbol = -3 から -6.5 まで拡がっていて、ピークは Mbol = -4.875 である。 SMC の観測 CSLF SMC の観測 CSLF は Groenewegen 1997 が Rebeirot et al 1993 の観測した 1636 星 に Westerlund et al 1986 の輻射補正を当てはめて求めた。距離指数 = 19.0 が 採用された。この CSLF の最初のビンには Mbol ≥ -2.5 の炭素星すべてが含まれて いる。このビンの星は全体の 3 % 以下である。それらは Mbol = -1.8 まで達し、第3 ドレッジアップで形成された炭素星とは考えにく |
い。これらの星は連星内の質量
移送で作られたと考えるのが自然であろう。この論文では Mobl = -2.5 より明るい
炭素星のみを考える。CSLF は Mbol =-6.5 まで延び、ピークは Mbol = -4.375 である。 MIR フラックスの効果 最近、Guandalini et al 2006 は MIR フラックスを考慮すると CSLF は もっと明るい方へずれると主張した。彼らの主張は銀河系の MIR 観測が ある炭素星に基づいており、赤外で明るい星にバイアスがかかっている可能性 がある。彼らのサンプルの多くが J-K > 2.0 であることもこの推測を 裏付ける。van Loon et al 2005 によれば、LMC のダスト炭素星の割合は 10 - 20 % である。したがって、MIR フラックスが CSLF を大きく変えることは ないと考える。 4.2.TP-AGB 寿命:M-型星とC-型星マゼラン星団の巨星寿命マゼラン雲星団中、Mbol < -3.6 の M-型星と C-型星 の寿命が最近 Girardi, Marigo 2007 により導かれた。 基本的には、質量範囲 1.5 - 2.8 Mo の炭素星 の寿命は 2 - 3 Myr である。寿命ピークは SMC の方が少し低質量に来る。M-型 巨星の寿命のピークは LMC では 2 Mo の時 4Myr で、SMC ではデータの質が悪く 決められなかった。 モデルと観測の一致基準 我々は 0.8 - 5 Mo の星に対し、TP-AGB 寿命を Girardi, Marigo 2007 の値を 67 % 信頼度レベル(最も混んだビンで 1 σ )で定めることを目標とする。 多くの TP-AGB モデルはこの基準を満たさず、非常に短い炭素星の割合を与えたり 寿命全体の傾向が再現されなかったりするので、この基準は実際には有用である。 |
|
CSLF の再現過程は以下のようである。 (1)静謐期の進化経路を集める。 (2)内挿により等時線を定める。 (3)等時線の炭素星部分を分離する。 (4)Wagenhuber, Groenewegen 1998 の手法で熱パルスサイクル光度変化決定 (5)各静謐点毎に光度確率関数を決める。 (6)静謐点を積分して、ある SSP に対応する CSLF を決定。 (7)恒星集団の年齢に渡り、AMR と SFH を用いて積分して最終 CSLF を得る。 SFR は CMD フィッティングから決定 LMC の SFR は Holtzman et al 1999 を採用した。これは Hodge4 付近の LMC 外辺部 HST データの解析から得られたものである。SMC に関しては Harris, Zaritsky 2004 MCPS による全体の SFR を用いた。どちらの SFR も |
CMD フィッティングにより
得られた。フィッティングは主に AGB より前の進化段階の星の数で決まるので AGB 進化
の詳細には無関係である。 AMR AMR の決定には Pagel, Tautvaisiene 1998 のバーストモデルを用いた。この関係は 理論的ではあるが、星団の年齢メタル関係を再現するように選ばれた。 TP-AGB 寿命の比較 TP-AGB 期の M-, C-型星寿命は進化経路から直接得られる。進化経路から求めたターン オフマスを変数にして内挿し、ターンオフマス - TP-AGB寿命関係を各メタル量毎に作り、 さらに 年齢 - メタル関係を使って、ターンオフマス - TP-AGB 寿命関係を作り、 Girardi,Marigo 2007 関係と比較する。 SW 期間 現在のマスロス式だと SW(-dM/dt > 5.6 × 10-7 Mo/yr) の 期間は Z ≤ 0.008 の全進化経路に対し 20 % 以下である。特に 1.5 Mo ≤ M ≤ 2.5 Mo 範囲ではそれが 15 % 以下になる。 この値は van Loon et al 2005 の マゼラン雲ダスティ炭素星の割合と大体は合っている。しかし、もっと詳細な検討 が必要で、今後の論文に任せる。 しかし、これらの星の扱いはパラメター較正に大きくは影響しない。 |
|
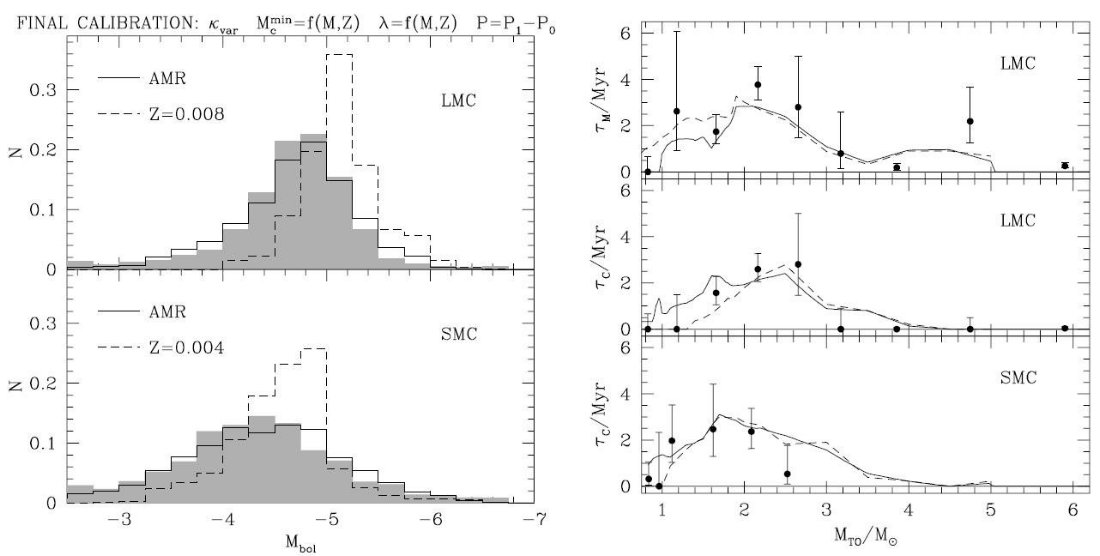
付録に述べる較正から以下のような興味深い事実が明らかになった。 (1)CSLF と TP-AGB 寿命を同時に満たすという制限 マゼラン雲の CSLF と C-, M-型星寿命を併用することで、TP-AGB モデル の信頼性が向上した。実際、片方だけを満たすがもう片方をはずすモデルが存在する。 (2)ドレッジアップのメタル量依存性 第3ドレッジアップがメタル量に強く依存するので、炭素星種族の解明には メタル量増加の歴史を考慮し、Z = 一定の条件を緩めるべきである。実際、LMC, SMC 双方の CSLF を同時に再現しようとすると、図27に見られるように、Z = 一定では 明るい炭素星が多くなり、一方暗い炭素星が足りなくなる。この問題は第3ドレッジ アップのメタル量依存性を考慮し、適切な AMR を計算に含めると解消する。 |
すると、暗い炭素星が作れないという炭素星ミステリーはそれ程深刻で
なく、単に観測とモデルを対比する際のメタル量のミスマッチということになる。 その上、二つの銀河のメタル量範囲が Z = 0.004 を中心にして分布していて重なって いるので、第3ドレッジアップの較正に強い制限がかかった。 (3)M-型星寿命のピーク マゼラン雲星団に見られる M-型星(RGB-tipの先)寿命のピークを再現するためには Z = 0.008, M = 1.7 - 2.5 Mo の星では第3ドレッジアップが始まるのは TP-AGB と 同時ではなく、それより少し後にしなければならない。Karakas et al 2002 による Mcmin 定式化は上の結果と合致する。こうして、Cioni et al 2006 の計算 で問題となった M-型星が沢山作れないという問題が解消された。 (4)高質量炭素星の寿命低下 Mi > 2.5 Mo で炭素星寿命が減少して行くのは、光度が上がり SW 開始が早まり、 また、M ≥ 4 Mo では、HBB が起きて C を O に変換するからである。 |
|
(1)可変分子オパシティ 今回最も大きな改善は可変分子オパシティの導入である。このオパシティは以前も http://pleiad.oapd.inaf.it などで使われてきた。しかし今回のモデルはパラメター の較正が行われた初のモデルである。 (2)較正 モデル較正には CSLF とTP-AGB 寿命の双方を用いた。その結果、積分光度に対する TP-AGB 星の貢献も Renzini,Buzzoni 1986 の Fuel Cosumption Theorem で述べられ ているように正確になった。これはマゼラン雲銀河メタル量に対しての較正である。 |
(3) 第1熱パルス前のモデル 今回のモデルはGirardi et al 2000 の第1熱パルス前までのモデルの後を補うもの である。両者は大きな不連続なしにつなげることが可能である。 (4)脈動モード 脈動モードの転換を初めて進化コードに取り入れた。これは変光星との比較により この進化モデルを新たな方法で較正する可能性を開くものである。 |
|
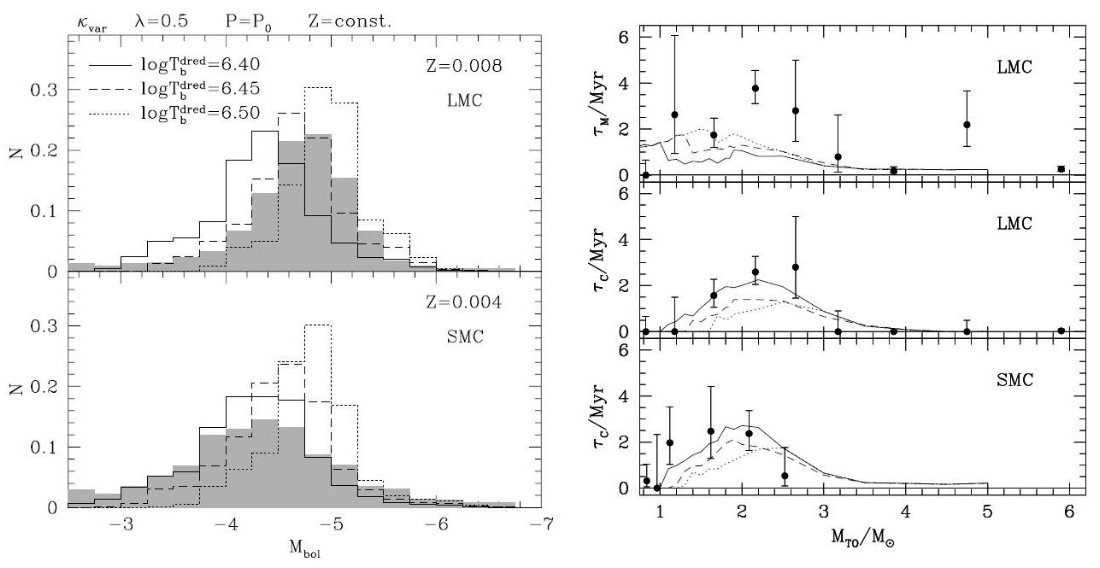
ドレッジアップパラメター 図A1 は、第3ドレッジアップを Marigo et al 1999 と同じ方式で 扱った計算結果を示す。マスロスも Vasiliadis, Wood 1993 の方式を採用し, 常に基本振動とした。大きな違いは分子オパシティを可変型にしたことである。 |
結果の比較 (log Tbdred = 6.40, λ = 0.5) セットは Marigo et al 1999 では CSLF のベストフィット を与えたが、もはや再現しない。炭素星寿命は LMC, SMC でうまく回復しているが。(log Tbdred = 6.45, λ = 0.5) セットは CSLF をまあ再現するが、炭素星寿命が少し短すぎる。 (log Tbdred = 6.50, λ = 0.5) セットはすべて観測と合わない。 指摘しなければならぬのは、どのドレッジアップパラメターの組み合わせも SMC の CSLF を再現しなかったし、M-型星寿命が Mi = 1.8 - 3.0 Mo の区間で短すぎた。 |
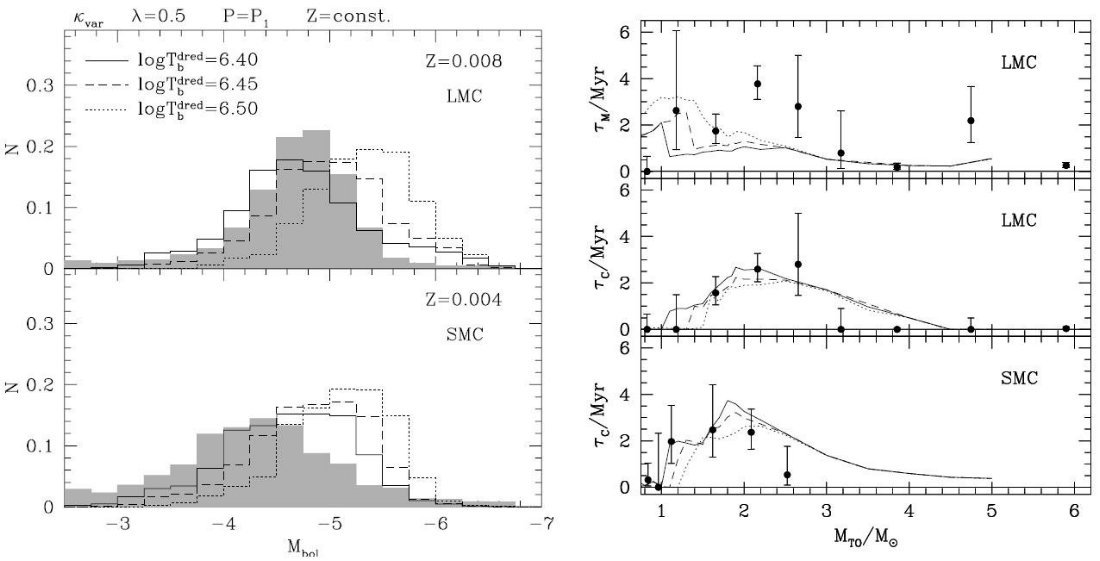
| 図A2は基本振動の代わりに第1倍音を仮定した。短周期になったため、 マスロスが抑えられ、TP-AGB 期が延びて明るくなる。このため、CSLF は明るい 方に片寄る。 | どの(Tbdred, λ)セットも CSLF を再現できない。炭素星の 寿命はかなり良く合わせられる。しかし、M-型星寿命は相変わらず短い。 |
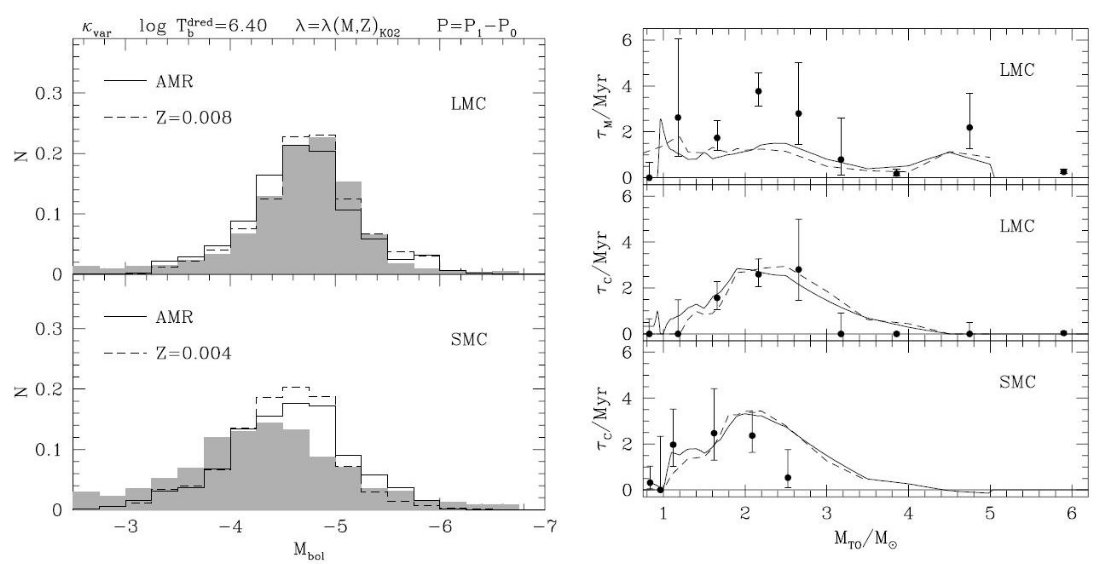
|
A3の新しい点は、 (i) λ = 一定をはずし、質量とZにより可変とした。 (ii) 脈動のモード転換を入れた。 (iii) AMR を考慮した。 | 実際には、λ(M, Z) の採用は LMC の CSLF 再現に有効であった。 ただ、SMC では明るい炭素星が多く作られ過ぎる。その上、M-型星の寿命が 短い問題は依然として残されている。 |
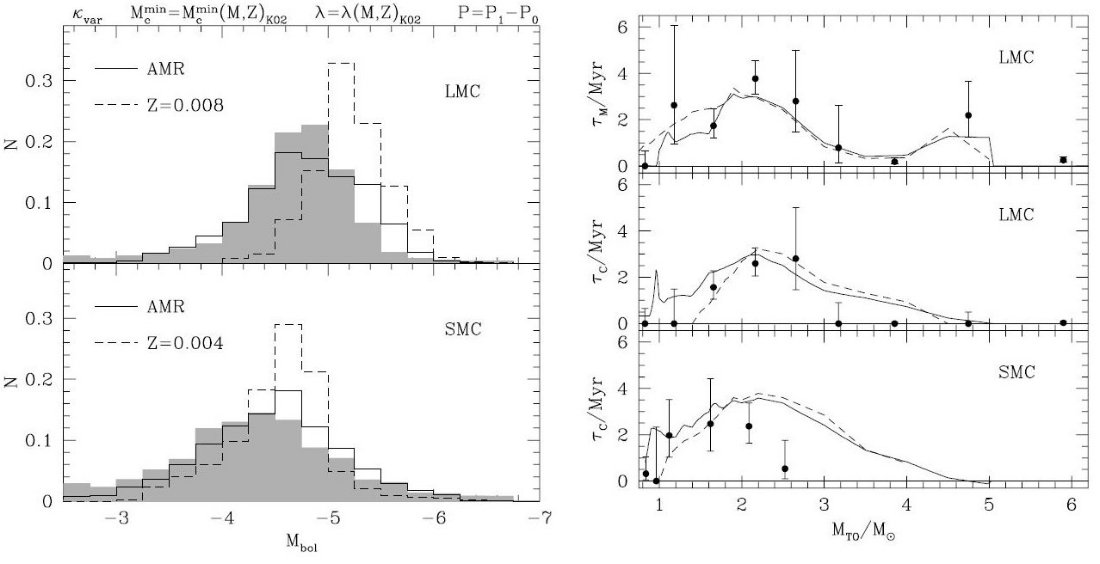
| その問題は第3ドレッジアップの開始をTbdred から Mcmin (M,Z)(Karakas et al 2002)へ変更することで解決した。以前は Mi ≥ 2 Mo では 第1熱パルス開始時に既にドレッジアップが始まっていたが、それが遅れ、M-型星 の時間が延びたのである。 |