From Wind to Superwind: The Evolution of Mass-Loss Rates for Mira Models


G.H.Bowen, L.A.Willson
ApJ 375, L53 - L56 (1991)
Bowen, Willson 1991 PDF　はここをクリック



　アブストラクト　

　ミラ型変光星の大きなグリッドに対して動力学的大気モデルを計算した。星は 太陽組成で、M = 0.7 - 2.4 Mo, P = 150 -800 d をカバーしている。振動は 基本モードである。進化の結果、質量放出率は上昇する。超星風は殆どのモデルで 起きた。ダストはそれを助けるが必要条件ではない。非常に低メタルな星でも この超星風は起きる。しかし、その場合は高い光度である。これは、銀河初期の 低メタル種族での超新星にとって大きな意味を持つ。





　１．イントロ　

　Reimers　の式　

　質量放出に関しては、Reimers 1975 の経験式が広く用いられている。

　　　　　(dM/dt) = -4 × 10-13η L R / M

この関係式は AGB 全期間を通して観測と合致しているわけではない。その増加率は 小さすぎ、また最大放出率も小さすぎる。Renzini 1981 はこれよりずっと大きな 星風が決定的な時期に起きると考えそれを「超星風」と名付けた。その起源に 関しては多くの考察 (Iben,Renzini 1983, Iben 1987) がなされた。 		　　 　質量放出星モデルのグリッド　

　この論文では、ミラ型変光星を対象に、広い範囲のグリッド上で動力学的モデル を計算し、AGB 進化の間に星に起こる様々な変化の結果、質量放出率がどう変わるかを 示す。その効果は劇的であった。初めに、総質量一定のまま核反応が進行して核 質量、光度、半径、脈動周期が増大する。大気が膨張し、質量放出率は時間の 指数関数的に上昇して行く。質量放出のタイムスケール = -M/(dM/dt) が核成長 のタイムスケールより短くなると、質量放出が進化の支配要因となる。そして 星の外層は急速に失われて行く。大規模質量放出の末期には太陽組成の星の モデルは OH/IR 星と似る：つまり、巨大で明るくとても長い周期を持ち、 -(dM/dt)/M ∼ 10-5 - 10-4 (Mo/yr) で厚い ダストシェルに覆われている。最終質量は惑星状星雲中心星 (Weidemann 1987) の それと予想される。

　超星風は確実に起こる　

　ここで強調しておきたいのは、それらの結果は人為的にそうなるようにして 得られたものではないということである。超星風を仮定したり、特別なメカニズム を付け加えたり、パラメターを調整したりはしなかった。パラメターに対する計算 結果の依存性をチェックして得た結論は、

（１）超星風は確実に存在する。どのパラメターの組み合わせでも発生した。

（２）超星風発生時の光度やコアマスは星質量とメタル量で決まる。

したがって、他のモデルパラメターの選択は基本的な結果にあまり影響しない。 ここで述べる結論は人為的なものでなく、現実の星に起こる事実に近いと信じる。

　２．方法　

　計算法　

　詳しい計算法は Bowen 1988a,b に述べられている。簡単に言うと、動力学的及び 熱力学的方程式を球対称な星に適用する。ショックを扱うためアーティフィシャル ビスコシティーを導入した。熱的緩和の進化とダストへの輻射圧効果も組み込んだ。 モデルの内側境界は光球の内側、脈動の駆動域に置かれ、サイン関数的に動かされる。

　半径と光度の決定　

　モデルを特性付けるパラメターは星の質量 M, と基本振動脈動周期 Po である。 それらのパラメターに対応する半径 R は Ostlie, Cox 1986 の, 周期 - 質量 - 半径 関係から得られた：

log Po = -1.92 - 0.73 log M + 1.86 log R 　　(2)

　光度 L は Iben 1984 の 半径 - 光度 - 質量 関係から得られる。

R = 312 (L/104Lo)0.68(M/1.175Mo)-0.31S (Z/0.001)0.088(l/Hp)-0.52　(3)

有効温度 Teff は、L = R2 Teff4 から決まる。単位は、 Po が日、M, R, L は太陽単位 である。M & le; 1.175 Mo に対しては S = 0, 他は S = 1 である。特に断らない場合、(l/Hp) = 0.90, Z = 0.02 とする。

　基準モード振動　　

　全てのモデルは基本モードで振動している。最近、観測に基づいて、ミラは基本 振動をしているという議論, Willson 1982, Wood 1990 が盛んである。さらに Bowen 1990 はそうであるべきという理論的裏付けを与えた。密度勾配の結果、 周期がある値以上の波は光球付近で反射される。Stein, Leibacher 		1974。 ミラ の場合、その周期は正に音波エネルギーが大気に伝達されて第１倍音振動は強く 弱められ、しかし基本振動は殆ど弱められないような領域にある。

　注入エネルギー　

　内側境界の速度はそこでモデルに注入されるエネルギーの最高値 が星の光度と一致するように選ばれた。その理由は次のようである： 星内部の動力学モデルは小振幅振動の成長率に非常に大きな値を 与える。従って、何が次際の星ではある振幅に抑えているのかは 問題であった。Ostlier, Cox 1986, Wood 1990. 我々のモデルでは、 大振幅脈動を駆動するための運動エネルギー注入量は光度 L に近 づいて行く。それが上限になることは明らかであるが、星の振幅は 駆動領域が与えられる最大エネルギーよりは低い値で振動している。 駆動領域は膨張、収縮を繰り返し、様々な割合で正や負の仕事を している。

　境界速度　

　こうして、我々は広い範囲のパラメター空間で矛盾のない脈動を 得ることができた。内側境界の速度は通常 2 - 3 km/s である。そこ から発生するショックの最高速度は 26 - 36 km/s である。この結 論は仮定した駆動パワーの最高値にはあまり依らない。

　ダスト吸光断面積　

　ダストもモデルに加えられた。ダストの吸光断面積は熱平衡ダスト温度の 関数と仮定し、最も冷たい箇所で、 Γ ≡ (arad/g) = 1.00 となるよう調節される。この選択は、 Γ < 0.5 だと殆ど効果が なく、 Γ > 1.0 だと外側向きに急な加速を起こすことから決め られた。もし、 Γ > 1.0 だとダストは急激にその領域から運び出さ れてしまい成長できないだろう。通常、グレインの凝集温度は 1350 K と されている。輻射吸収断面積から T = 1350 K で、 Γ = 0.50 で効果 が小さいが、 T = 1000 K では、 Γ = 0.97 とする。最近の Danchi et al 1990, Bester et al 1991 の結果を見るとこれらの温度は もっともらしい範囲である。
Γ ≡ (arad/g) の a, g は輻射と重力の加速度？

　３．結論　

　光度変化　

　図１はモデルパラメター一定の線を示す。質量放出計算の結果は図２に示す。 質量放出と進化の関係を示すために Paczynski 1970 の L - Mc 関係を 用いた。

　　　　　L = 59,250 (Mc - 0.522) 　　　　　　　　　(4)

この関係式はどちらの図にも載せてある。式 (4) は dL/dt ∝ dMc/dt を 意味し、L ∝ dMc/dt なので、数値を入れて、dlog L /dt = 0.245 Myr -1 を得る。1Myr にlog L が増加する大きさ 0.245 は図２右下 に示されている。このように、核反応進化は図上で星を右方向水平に動かすように 働く。つまり、横軸は時間軸と看做せる。

　質量変化　

　図２上進化矢印の縦方向はモデル計算の (dlog M / dt) から決まる。与えられた 星の進化経路は矢印をつないで得られる。各経路上で、ゆっくりした核反応進化 から超星風による急速な質量放出進化への転換点がある。残存核質量の大きさ はこの進化経路が L - Mc 関係線とぶつかるところで決まる。

　図２には、log[-(dM/dt)/M (yr-1] = -9, -8, -7, -6, -5 のライン も引いた。dlog L /dt = 0.245 Myr-1 であるから、進化経路が勾配 -1 を持つのは、-(dM/dt)/M = 5.65 × 10-7 yr-1に なる時である。したがって、今述べた (dM/dt)/M 一定ラインは、進化経路の勾配 = -0.0018 から -18 に対応する。これらのラインが水平方向にほぼ等間隔で並ん でいることは、-dM/dt が近似的には指数関数的に増加して行くことを意味する。
進化経路が水平な時は正しい。傾いてくると誤り。

　パラメター変化に対する安定性　

　我々はモデル計算のパラメターを変えて、結果にどう影響するかを調べた。大抵 のパラメターを大きく変えても、超星風が起きる時期はほんの少ししか変わらなか った。例えば、LSW を -(dM/dt)/M が 10-6 yr-1 に達する光度と定義しよう。パラメターの大抵の変化に対して, | Δlog LSW | ≤ 0.04 であった。詳しくは後の論文に。

　超星風　

　何がこの超星風の原因なのだろうか？

　-(dM/dt) = 4 π r2 v ρ なので、dM/dt に影響するのは どのファクターかを知りたい。モデル計算の結果は明らかに、v ではなく ρ が星風領域全体に渡って増加していることを示している。では、なぜ ρ が 増大したのか？ショック波が形成される半径領域の内側では密度は半径の関数と して指数関数的に減少する。これは、対応する静水平衡大気と殆ど同じである。 その外側は強いショックと急激な加速が支配する領域である。そして、その 向こう側は星風領域である。そこではガス速度はほぼ一定で密度は r-2 でゆっくり減少していく。Bowen 1988b, 1990.



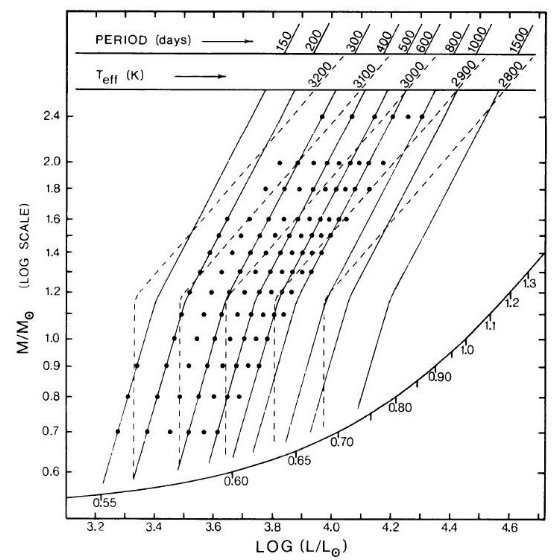
図１．式(2), (3)から導かれる星のパラメター。実線＝周期。鎖線＝温度。
　　　図下部の曲線＝Paczynski 1970 の L - Mc 関係　[式(4)] 		　この星風領域の密度は大気の最内側で密度がどのくらい低下するかによって決ま る。そこでの密度スケール高 H は H ∝ T/g ∝ R2T/M なので 進化の過程で大きく変化する。なぜなら、R, M はその間かなり変わるからである。 そして H は密度変化の式で指数関数の中に現れるので、星風領域の密度と dM/dt の双方共に H の変化に伴って大きく変化するのである。dM/dt が大きくなり、 M が減少すると、H と ρ は増加し、-dM/dt はさらに大きくなる。

　ダストの役割　

　質量放出におけるダストの役割は何であろう？星風の駆動メカニズムはエネルギーと 運動量の両方を供給すなければならない。ミラ型変光星に関して供給エネルギーは 10-4 L 以下で小さい。しかし、供給運動量 (dM/dt)vWIND は強い星風の場合 ∼ (L/c) に達し、この要請は厳しい。

　ダストは星の輻射運動量を受け取り、それを衝突によってガスに伝えことで 質量放出を助ける。Γ の最大値を 0.0 から 2.0 まで変えて一連のモデル 計算を行った結果によると、vWIND の増加が -(dM/dt) の 増加につながっている。星風密度はダストが存在しない内側領域で決まっていて Γ の値は関係しない。ダスト凝結温度の変化も、ダストの総吸光面積を 増加させるので Γ と似た効果を持つ。

　図２で質量放出率 -(dM/dt) > 2 × 10-6 Mo/yr のモデル は全て厚いダストシェルを持つ。ダスト量を変えるようなモデルの変化はそれに 対応した質量放出率の変化をもたらす。ダスト吸光断面積の増加は単に質量 放出率の増加に寄与するだけではない。それはその原因なのである。

質量放出は脈動なしでもダストだけで可能ということか？

　ダストなしの質量放出　

　しかし、ダストなしでもかなりの質量放出が可能である。例えば、M = 1 Mo, Po = 300 - 400 d でダストありとなしのモデルを計算すると、ダストなしでも ダストありモデルと較べ、-(dM/dt) で 0.1 倍、vWIND で 0.2 倍 の大きさで質量放出を起こす。何がこの星風を引き起こすのか？　どちらの場合 にもショック波の散逸による加熱が起きている。しかし、ダスト大気の場合、外側 大気の低密度で起きる、実際には断熱的な急激な膨張はガス運動学的温度を低い ままに保つ。ダストが無い場合、膨張はもっとゆっくりで、大気外層部に拡がった 高温域が生まれる (Bowen 1988a,b)。こうしてできた圧力勾配は遅い星風を産み出す。 等温ショックのモデルではこれは起きない。ダストなしモデルでの超星風の発生は 星の進化が進んで半径がさらに大きくなり、スケール高が延びて星風密度が 増加するまで延期される。この結果による光度変化は ΔL ≈ +0.12 である。

　低メタル星の質量放出　

　低メタル星の質量放出は次の二つの要因に影響される

（a）ダストの形成量が少なくなる。Z < 0.1 Zo ではダスト量が小さすぎて
　　　力学的な影響はほとんどない。

（b）与えられた R と L に対し、式 (2) は小さな R を与える。従って H は縮小
　　　し、ρWIND, -(dM/dt) は小さくなる。

そのため、超星風の発生は光度がずっと高い領域で起きる。低メタル星のグリッドは まだ計算されていない。しかし、やや低メタルな場合の結果によると、 Z < 0.1 Zo では上の二つの効果のため、Δlog L ≈ 0.12 - 0.13 log(Z/Zo) である。


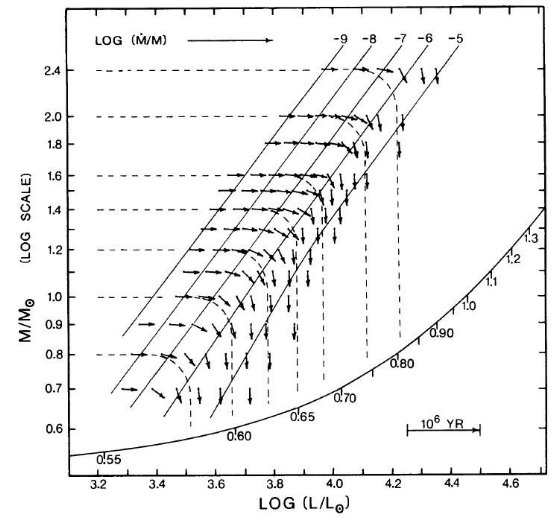
図２．図１モデルの質量放出と進化。各点での小さな矢印は進化の方向。
　　　実線は相対マスロス率 log [(-dM/dt/M] = -9, -8, -7, -6, -5　を示す。
　　　鎖線＝近似的進化経路。

　４．検討　

　熱パルス　

　熱パルスは星の半径、光度を大きく変化させる( ( Boothroyd,Sackmann 1988 ) ので 質量放出率に大きな影響を与える。しかし、予備的な計算によるとその積分効果 は総放出量に較べると小さいので今回の計算には含めなかった。しかし、それら は 1017 - 1018 cm の領域で、星周ダスト雲の構造には かなりの影響がある。分離シェルの形成 (Olofsson et al 1990) に関係するであろう。

　初期質量 - 終末質量関係　

　初期質量 と 終末質量の関係が図２の進化経路から示唆される。初期 AGB 質量 分布にこの関係を掛け合わせると、最終質量分布が得られる。これは惑星状星雲や 白色矮星の質量分布の研究にとり非常に興味深いテーマである。はっきり確定は していないが、最終質量分布が 0.6 Mo の周りにせまい巾でかたまっていることが 示唆されている。

　中心核の質量が 1.4 Mo に達する前に星の外層がすべて剥ぎ取られてしまう 星の最大質量はいくらだろう？図２の結果を外挿するとその値は 5 - 6 Mo と 		なる。そのような高い質量の星の系統的な計算はまだ行っていないので、観測され る白色矮星最大質量に対応する母星質量はまだ確定していない。質量が大きい星 では以下の効果が効いてくる。

(a) 分子に対する輻射圧の効果。

(b) 第１倍音振動の減衰が弱くなり、基本振動と第１倍音振動が共存するダブル
　　モードの脈動が見られる。

　非常に低メタルの星　

　非常に低メタルになると、超星風の発生が遅れて光度が大きくなる。AGB 期間 中の質料欠損が小さくなり、超新星の運命を免れるのはかなり小質量の星のみ となる。例えば、Z = 0.001 Zo では、Mi = 2.0 の星は Mf < 1.4 Mo であるが、 Mi = 2.4 Mo になるともはや 1.4 Mo には収まらない。太陽組成の恒星グループ と較べると、　超低メタル星の集団では非常に明るい AGB 星、多数の超新星 多くの高質量枠色矮星が特徴となる。銀河初期の化学進化はこの様な多数の 超新星により大きな影響を受けるだろう。