Low-Mass Stars III. Low-Mass Stars with Steady Mass Loss :
　　Up to the AGB and through the Final Thermal Pulses

４．結果と議論　

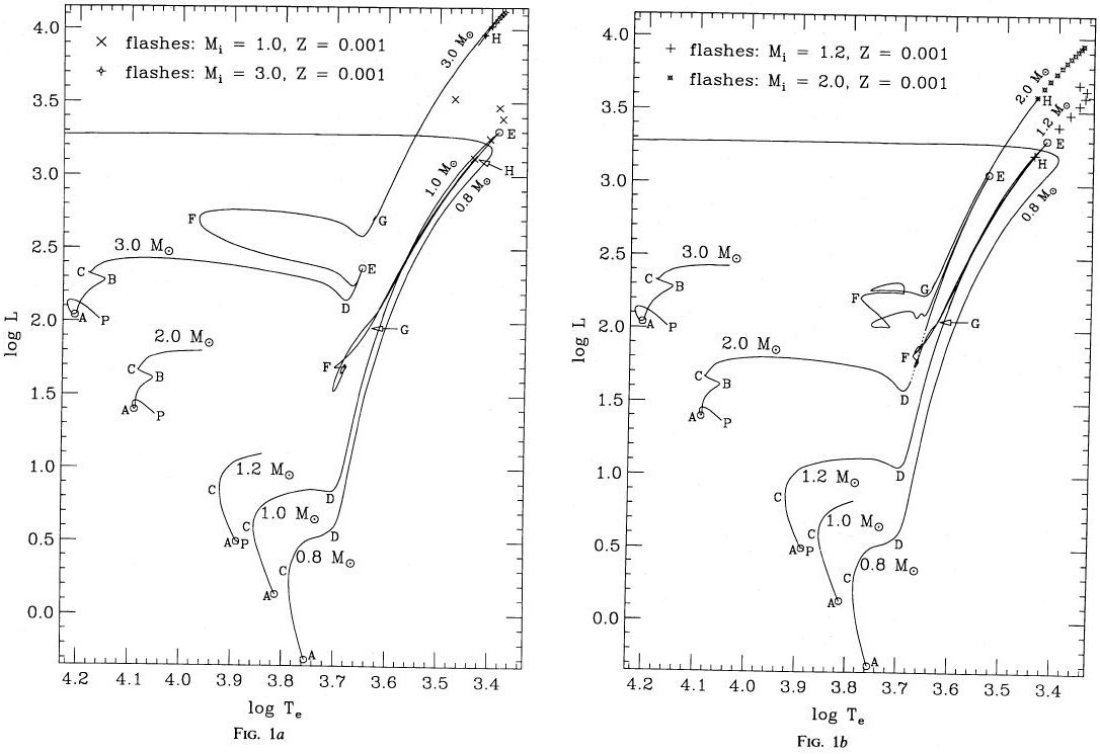
a) 前 AGB 進化　 　Z=0.001(図１) と Z=0.02(図２) の星の進化を計算した。α = 1 が使われている。 図１は混線を避けるため２つに分けた。Ｐ点はリアルではない。 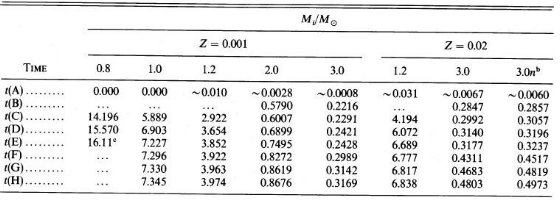表１　進化経路上の時刻 i) 進化の全体　 　大質量では CNO サイクルによる対流核が存在する。Ｂ点は核の水素がかなり欠乏して きた時、半径が主系列では最大、温度最低になる点である。低質量星ではｐｐチェイン が主で、Ｂ点は存在しない。 　Ｃは中心で水素が無くなる点で、水素殻燃焼が開始される。Ｄは赤色巨星枝の底である。 ヘリウム核が成長すると、星はRGBを登り始める。ここで、表面対流層の底が以前水素燃焼が 起きていた層の上端に届くと第１ドレッジアップが起こる。RGB 上部ではレイマース星風に よりかなりのマスロスが起こる。 E 点はRGB先端である。M ≤ 2.5 M๏ ではヘリウム核が縮退しており 爆発的なヘリウムフラッシュとなる。フラッシュ後の星はRGBを急速に下がり、ヘリウム核 燃焼状態に移る。Ｆ点はこの時期のブルーループ青端である。中心ヘリウムが減ってくると 星は低温側に戻り始め、Ｇ点で中心ヘリウムが消滅する。水素殻燃焼が停止し、ヘリウム 殻燃焼が始まると星は AGB を上がり始める。この時期を E-AGB と呼ぶ。質量の大きな星 ではここで表面対流層が水素ヘリウム境界層を突き抜け、第２ドレッジアップが起こる。 ただし、本論文で計算した質量ではそれは起こらない。 　ヘリウム燃焼殻が成長して H - He 不連続面に接近していくと、水素燃焼殻が再点火する。 その直後にＨ点で第１熱パルスが起きる。その先は TP-AGB と呼ばれる。熱パルスは外層 が殆ど消滅するまで定期的に発生し続ける。 　図１、２を見ると、有効温度がやや低い（太陽メタル量で Te ≈ 2000K まで） ことに気付く。これは、採用した α が小さすぎたためである。ほぼ、Te ∝ α1/2 である。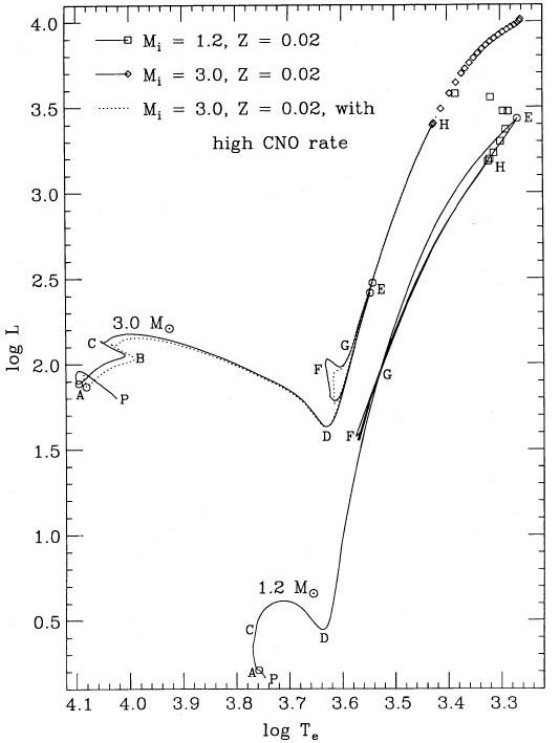

図２　Z=0.02 星の進化。M = 3 M๏ の点線では高いCNO燃焼率を採用。

ii) ヘリウムフラッシュ前の進化　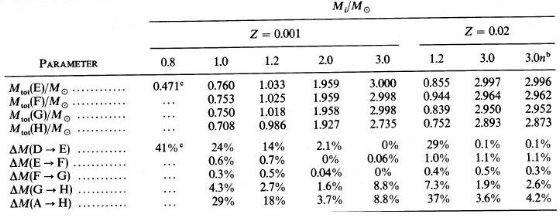 表２　レイマース星風によるヘリウムフラッシュ前のマスロス 　Renzini 1977, 1981 は球状星団に対し、0,85 M๏ で低メタル量 の星は RGB 上で 0.2 M๏ を失う必要があることを指摘している。 彼の計算は、η = 0.4 が最適であることを示した。しかし、本論文で採用した α, 分子オパシティは R を大きくし、結果として 0.2 M๏ Z = 0.001 星ではRGB 上で 0.33 M๏ が失われることとなった。 Z = 0.001 の 1.0, 1.2 M๏ 星で、それぞれ 0.24, 0.17 M ๏ が失われているので、なぜ「ので」かは？ マスロス率が 1.5 - 2 倍大きいらしい。 RGB マスロスについて　 　表２から分かるように、Minit が小さくなると RGB マスロス量は増える。目立った マスロスが RGB 上で起きるのは Minit ≤ 1.2 M๏ の場合である。 これは、マスロス率が M に反比例することからも予期されていたし、小さい星は RGB 寿命が長く、低温であることからも予想されることである。メタル量 Z を上げると、寿命 が伸び、温度が下がるので、 Minit = 1.2 M๏ で較べた時、Z = 0.02 が Z = 0.001 の倍のマスロス量を示すのは当然である。マスロス量が Z で変化するのは Renzini 1981 が示したように観測とも一致する。 　Minit ≤ 2 M๏ では、熱パルス前のマスロスは大部分 RGB 上 で起こる。もっと大質量でヘリウムフラッシュが起きない星では RGB 先端光度は 低質量星より暗く、しかし熱パルスは低質量星より明るい箇所で発生する。その場合、 熱パルス前のマスロスは主に AGB の熱パルス前に起きる。ただ、その量は小さい。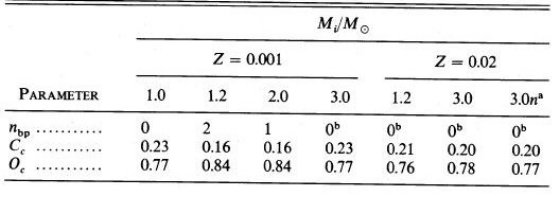

iii) ヘリウムフラッシュ　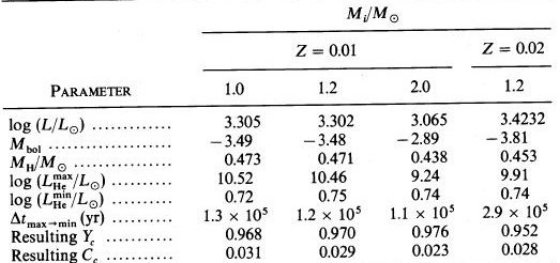 表３　ヘリウムフラッシュの強度と形成された炭素量。Ccは多分フラッシュ後の中心Ｃ比。 　本論文のヘリウムフラッシュ計算は非流体力学的コードに基づくが、何もないより ましである。表３にはヘリウムフラッシュの計算をまとめた。大体 Mc ≈ 0.45 M๏ でフラッシュを起こし終了後の炭素組成 Cc は 0.03 程度と小さい。 　Despain 1981 と異なり、トリプルアルファ反応のレートが上昇して、ニュートリノ 冷却の効果を打ち消し、発火が中心で起きたが、結果は同じであった。 　フラッシュのピークから、星がRGBを下がった後ヘリウム燃焼が極小になるまでの時間 は 105年程度である。 iv) ヘリウム核燃焼期の呼吸パルス(breathing pulse)　 　水平枝上、ヘリウム核燃焼期の間、Renzini 1977 は中心対流核のヘリウム量が Yc ≤ 0.1 まで減少すると、対流不安定が発生し、大量のヘリウムを核内に持ち込み、核反応パルス を引き起こすことを見つけた。Castellani et al 1985 はセミ対流層の扱いを改良し、この 過程を追い、ヘリウム核燃焼が終了するまでにこの様な呼吸パルスが３回起こることを見出 した。その結果、水平枝寿命が 40 % 延び、核の酸素が増加して炭素は減少した。 　このパルスの間、星は急速に青い方へ動き、パルスが終了するとゆっくり赤い方に戻る。 Lattanzio 1986 はこの結果を確認した。本論文も呼吸パルスの存在を確認したが、 この現象はセミ対流層の大規模で急速な変化を伴い、計算の精度は低い。低質量星の場合 にはこの現象が核質量に及ぼす影響は小さい。寿命が 40 % も 伸びたのに？ 表４　呼吸パルスと最終的な酸素、炭素存在比

b) AGB 上の熱パルス　 　熱パルスの数は、Z = 0.02 では、9 (1.2 M๏), 22 (3 M ๏), 17(3 M๏だが高いCNO率のテストラン) Z = 0.001 では、5 (1.0 M๏)である。1.2 M๏ では 7 回目までは α = 1.0, その先は、6-8 回目を α = 1.5, 6-10回目を α = 2.0, ６回目と７回目を α = 3.0 の計算を行った。Z = 0.001、M = 2 M๏ では α = 1.0 で１１パルスを、α = 1.5 で 10 - 17 パルスを計算した。Z = 0.001、M = 3 M๏ では 7 回の パルスが計算されただけであった。この星ではパルスは完全振幅に至っていない。 　i) 熱パルスの開始　 　熱パルスは LHe の小さな振動として始まり、ヘリウム燃焼殻が水素 燃焼殻に接近するに連れ急速に成長していく。有意な第１熱パルスは LHe max > L となった時で定義される。ヘリウム燃焼による対流層が出現 した時で定義することもあるが、ここでの例では両者は一致していた。表５にはこの 第１パルスが載せてある。Yenvは第１ドレッジアップの結果 0.01(3 M๏)から 0.02(< 2M๏)増加し、Cenv は 2/3 に減少(当初はC/Z=0.22)、 Oenv は不変である。 　図１，２を見ると、Minit≤1.2M๏ではだ１パルスＨ点が RGB 先端より低い位置にある。そのため、RGB と TP-AGB が重なる。しかし、本論文で 扱った星は全て AGB が RGB の先まで伸びている。もし、マスロス率を正しく下げたら さらに先へ伸びるであろう。したがって、最低星質量、例えばRenzini 1981 が扱った ような 0.85 M๏ の場合にのみ　RGB と AGB 先端は一致するので ある。それでも、重なりあいは観測者には面倒なことだが。 　図３は熱パルス開始時の光度 LTP を示している。Iben,Renzini 1983 よりずっと暗いところで発生していることが分かる。彼らは > 5 M๏ と < 1 M๏ の計算結果を内挿しているが、この領域では LTP がスムーズな変化を示さないことがずれの一因であろう。しかし、 高質量へ行っても一致しそうにない。一方、Lattanzio とは良く合っている。 　Minit ≤ 3 M๏ では、Minit に対する LTP の増加は 高メタル量星の方が低メタル星より緩やかである。LTP が低いということは ドレッジアップが起きる前に熱パルスがそれに必要な強度にまでなっていられるという 意味で、炭素星の形成にとって重要である。何のことやら？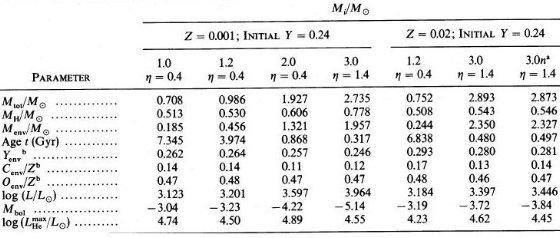

表５　第１熱パルスの状態。 　　　3.0n は高ＣＮＯ反応。 Yenv, Cenv, Oenv は第１ドレッジアップの結果。 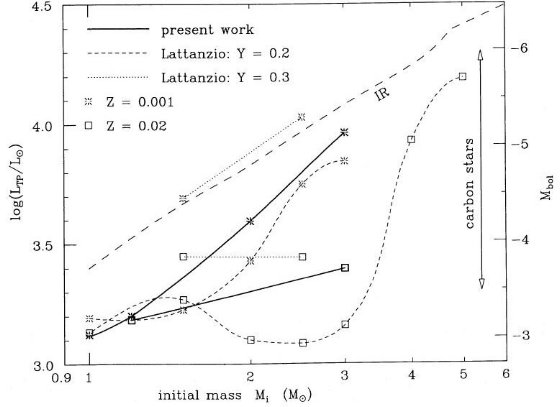図３　熱パルス開始光度。実線＝本論文。鎖線＝Iben,Renzini 1983(Z=0.02) 　　　点線＝Lattanzio 1987(Y=0.3), 短鎖線＝Lattanzio 1987(Y=0.2) 　　　Y 依存が強いことに注意。

ii) パルス強度の成長　 　パルス強度、すなわちヘリウム光度の最高値 LHemax、は 初め急速に成長する。10 パルスくらい経つと「フル強度」に達し緩やかな増加に 転じる。図４は核質量に対し LHemax をプロットした。 対数でなく実数で見ると、 LHemax は Mc または回数に対し 線形に増加していることが分かる。ドレッジアップがない状況ではこの増加が平坦に なる徴候はない。 　図４から分かるもう一つの重要な点はパルス強度は低メタルでより急に成長する ことである。Z=0.001, Minit=1.2, 2.0 M๏ では 10 パルス後に LHemax = 7×107L๏ で あるが、。Z=0.02 では, Minit=1.2 M๏で 2×106 L๏、 3.0 M๏ で 1×107L ๏である。 　他と比較すると、Hollowell 1987 はマスロスなしの Z = 0.001, Minit = 0.7 M๏ で第１６パルスの時、 LHemax = 1.5×108L๏, Lattanzio 1987 は Z=0.003, 0.006, Minit = 1.5 M๏、マスロス なしに対し、 107L๏ を得た。論文IVで述べるように、 熱パルスが強くなるほどドレッジアップに都合がよい。したがって、低メタル星ほど 楽になるわけである。 　図４を見ると、 LHemax を Mc の関数として表わすのは 困難である。従って、良くやられるように勝手に外層マスを増やしたり減らしたり して、異なる Minit の進化をシミュレートするのは不正確な結果になる。

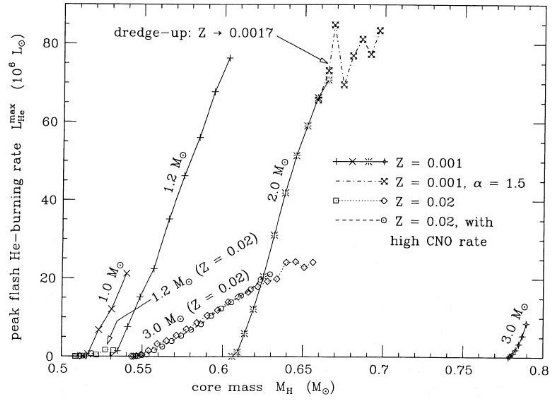図４　熱パルス極大強度 LHemax の変化。 　　　実線(Z=0.001), 点線(Z=0.02), 点鎖線(2M๏, Z=0.001, α=1.5)

iii) 熱パルス期のマスロス　 　マスロス率の変化　 　図５にはパルスサイクル毎の平均マスロス率をプロットした。その大きさは 大体 10-7M๏/年程度である。レイマースの式を 見ると、マスロス率は L×R に比例するから、AGB を上がっていくとマス ロス率は MH より速く上昇する。それは図５に現れている。 　マスロス率は半径 R を通じて、 α によっても変化する。例えば、Z=0.001, Minit = 1.2 M๏ では、 3.9 × 10-7M๏/年 (α=1.0), 2.9 × 10-7M๏/年 (α=1.5), 2.2 × 10-7M๏/年 (α=2.0) である。 また、Z=0.001, Minit = 2 M๏ では、MH = 0.66M๏, Mtot = 1.73 M๏ の時に、 α による変化は、 4.8 × 10-7M๏/年 (α=1.0), 3.4 × 10-7M๏/年 (α=1.5) である。これ は、α が上がると R が下がる効果である。 　最後の熱パルスまで計算したのは、Z = 0.001 で M = 1.0M๏, 1.2 M๏(α=2.0), Z = 0.02 で M = 1.2M๏ のケースのみである。図５を見ると分かるように、それらの最後の２パルスは マスロス率が鈍化、または低下している。これは外層マスが消滅しかけて、星の収縮 が始まってきたためである。 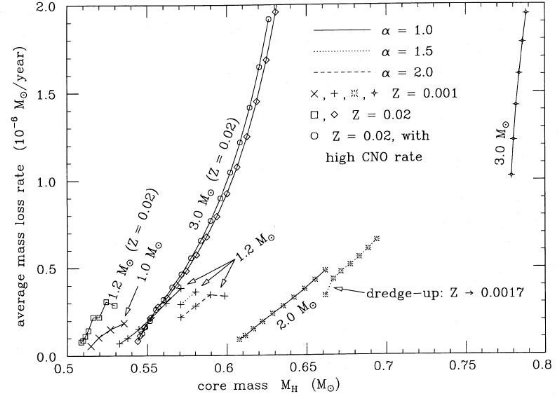図５　パルスサイクル毎の平均マスロス率。Minit = 3 M๏ の時 だけ η = 1.4 で、他は η = 0.4 である。実線は α = 1.0, 点線は α = 1.5, 鎖線は α = 2.0 である。2 M๏ では ドレッジアップで大気メタル量が上昇し、マスロス率が上がることに注意。 　　左端の２本と中央 1.2 M๏の右端、計３本は最後の熱パルス まで計算している。最終２回の強度鈍化に注意。

マスロスによる熱パルス回数の変化　 　前に述べたようにレイマース星風は RGB 段階でもかなりのマスロスを引き起こす。 図６にあるように、AGB では L と R が大きいため、さらに強いマスロスを生む。 強いマスロスは熱パルスの回数を制限する。例を上げると、 Z Mi 回数 0.001 1.0 5 1.2 8 第６パルス前をα=2にすると10回 2.0 30 図６をMtot=Mcに外挿して。Mf=0.77 3.0 30 Mf=0.85 0.02 1.2 9 3.0 25 　IIIa で論じたように、ここで使ったマスロス率は倍ほど大きかったようである。 もしマスロス率を半分にすると、熱パルス回数は増加する。しかし倍増はしない。 図６で Mc に対するマスロス率が半分になったと仮定して図を書き直し、そして カーブを外挿してみよう。すると、 Mi=1, 1.2 M๏ では 6 回、 Mi=2, 3 M๏ では 12 回程度増加することが推定される。これ らの回数は他の詳しい計算結果と大体一致する。 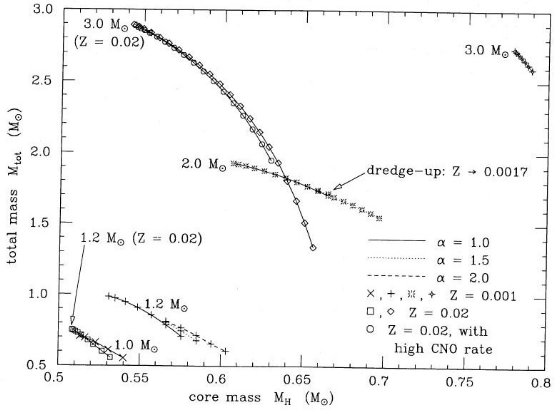図６　マスロスによる質量変化。α によるマスロス率の変化に注意。 　　　ドレッジアップによる大気メタル量増加による変化にも。 　　　左下の最終熱パルスまで計算した３本のみが Mf を直截に与える。

Mi - Mf 関係　 　上に述べた Mtot ≈ MH は星の最終質量を決定する。右の 表６にはレイマース星風によるマスロスを仮定して行った計算に、マスロス率 が半分になった時辿りついたどうやるのか知らない であろう最終質量を載せた。その値は図７にプロットしてある。 　最後まで計算したZ = 0.001 で M = 1.0M๏, 1.2 M๏(α=2.0), Z = 0.02 で M = 1.2M๏ のケースは、確かに表６の通り図６のカーブを横に倍に伸ばした値が書かれている。 では、計算が途中で終了している場合はどうしているのか？ Z = 0.001 で M = 2.0 M๏ を図６で見ると、Mtot = 1.5 M ๏ 付近で計算が終了している。その線を延ばすと表６にある 0.77 M๏ あたりで Mtot = Mc になるとも言える。ただそれが 0.8 ๏ であってもおかしくないのが困るが。もっと困るのは、 熱パルス開始のMc = 0.6 M๏ から　0.77 M๏ まで を倍に伸ばすと、0.95 M๏ になり表６の半分レイマース星風の値、 0.85 M๏ と大きく狂うことだ。0.85 M๏ にする には、半分星風に切り替わる時期を図６で計算が終了している Mc = 0.7 M๏ にしなければいけない。ウーン、本文中にそんな記述があった かなあ？ 　Z=0.02, M = 3 M๏ では確かに、Mc = 0.67 M๏ はもっともらしい。しかし、半分レイマース星風は Mc = 0.73 M๏ だから、0.61 M๏ から半分になるとしていることになる。なぜそこ からかは？ 　Mi - Mf 関係は Weidemann. Koester 1983 が年齢の分かっている銀河星団中の 白色矮星を使って導いた。Weidemann 1984 は惑星状星雲中心星の質量分布を用いて この関係を、小 Mi 領域に伸ばした。図７にはAaronson, Mould 1985 が　LMC, SMC 星団の AGB 先端光度に Mc - L 関係を適用して　Mc を、星団年齢から Mi を出し て決めた Mi - Mf 関係もプロットしてある。 Mc - L 関係には論文II の式を 使ったが、結果は彼らの図５と同じになった。 　超星風(super wind)　 　図７から、 Mi が小さい時には理論と観測の一致が良いことが分かる。Mi $le; 1.5 M๏ では Z = 0.001 理論線は Aaronson, Mould のデータ 点をもろに突き抜けている。また、Z = 0.02 理論線はWeidemann 1984 の高メタル 関係と矛盾しない位置にある。 　しかし、Mi が大きくなると、Mf が観測値より大きくなっていく。η の調整 では観測に合わせられない。Z = 0.001, 3 M๏ では、η = 1.4 を使っても Mf は Aaronson, Mould 1985 よりずっと上になってしまう。また、 Z = 0.02, 3 M๏ の Mf は Weidemann ラインより上になる。 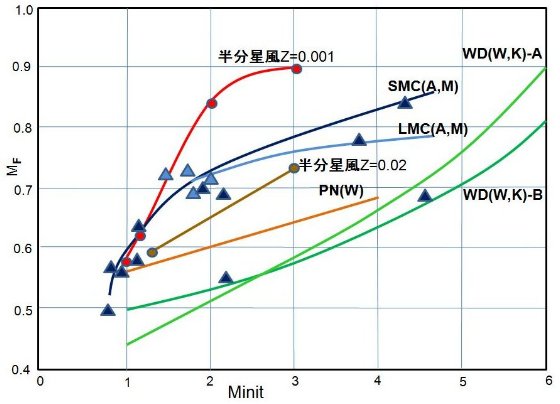図７a　Mi - Mf 関係。赤丸と黄丸は本論文の計算結果。青三角(LMC)と紺三角(SMC) は星団のAGB 先端光度から(Aaronson,Mould 1985)。SMC(A,M)とLMC(A,M) は三角印に 対して著者が引いた。WK-AとWK-B は Weidemann,Koester 1983, W は Weidemann 1984.

どうやら、ある限界質量 MWK が存在し、Mi ≤ MWK では レイマース星風で観測 Mi - Mf 関係を説明できるが、その上では追加マスロスが必要 になるらしい。図７を見ると、Z = 0.001 で MWK = 1.5 M๏, Z = 0.02 ははっきりしなくて、1.2 M๏ ≤ Mi ≤ 3 M ๏ であろう。　 　かなり強いマスロスが存在しなくてはいけない理由は他にもある。外層の流体力学 計算によれば、光度が上がると脈動が激しくなり大量の質量を放出する。また、 OH/IR 星の観測ではマスロス率が　10-5 - 10-4 M๏ /年　に達する。これは、レーマース式の１− ２桁大きい値である。(Werner et al. 1980, Baud,Habing 1983) 　熱パルス開始核質量 MHTP　 　図７b には熱パルス開始核質量 MHTP がプロットされている。 Z = 0.02 では MHTP は 1 M๏ ≤ Mi ≤ 3 M๏ では Mi に依らない。しかし、Z = 0.001 になると MHTP は Mi に伴い急増する。この点に関してこれまでの 研究結果は互いに一致した結論を出している。 　図７に関する最後の注意　 　Z = 0.001, Mi = 3.0 M๏ では Mc が　Mi - Mf 関係線 を越えるまで熱パルスが発生しない。一方で、Z = 0.001, Mi =2.0 M๏ では最終マスに達する前に 20 回も熱パルスを経験している。Z = 0.001 では 低質量の星（M ≤ 2 M๏）は炭素星になるのに十分な回数の 熱パルスを経験すると言ってよいだろう。一方、高質量（M ≥ 3 M๏ ）だとそうではない。これは Weidemann 1984, Aaronson, Mould 1985 の 結論と合致する。おまけに、論文IV で論ずるが、星風強度を弱めると、熱パルスが 起きてもドレッジアップを阻止するようになる。このようにマスロスは AGB 進化 と炭素星形成に大きな影響を及ぼすのである。 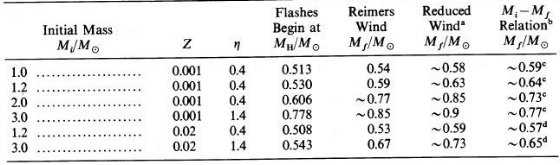表６　レイマース星風による最終質量。Mf は図６でマスロス率を半分にして 推定した。一番右のMi-Mf関係は観測値。cはAaronson,Mould, d は Weidemann 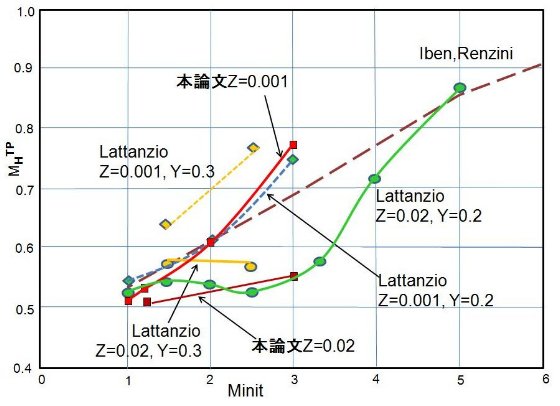図７b　Mi - MHTP 関係。

iv) 熱パルス対流層の Mc - Tb 関係　 　図８に示すように、低質量星の Mc≡MH と熱パルスで発生した 殻間対流層の底の最高温度 Tb との間には一般的な関係が存在する。しかし、 Iben,Truran 1978 が高マス星で示した Mc-Tb 関係を外挿しても低質量星の　Mc-Tb 関係にはならない。その IT 関係は以下のようである。 　　　　　Tb = 310 + 285 (MH - 0.96)　　　(2) ここに Tb は 106K 単位である。図８にあるように、この関係式は ここで得られたラインのずっと下を通る。 　他の研究結果も合わせると、低質量星の Mc-Tb 関係は組成依存性があるらしい。 とにかく、 Malaney, Boothroyd 1987 の結果は 　　　　　Tb = 250 + 305 (MH - 0.53),　　　MH < 0.65 　　　　　　　= 290 + 67 (MH - 0.65),　　　　0.65 < M H < 1 であるが、使用には注意が要る。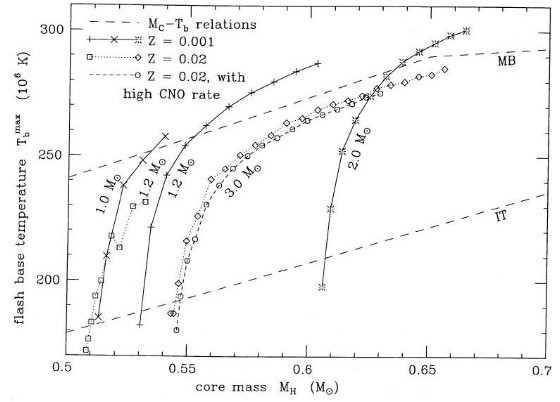

図８　核質量ー底温度関係。実線は Z = 0.001 星の進化。点線は Z = 0.02 星。 鎖線は Mc - Tb 関係。IT = Iben,Truran 関係。MB = Malane,Boothroyd 1986 関係。

v) 熱パルスで出来た炭素ポケット　 　熱パルスによる殻間対流層が退いた後には炭素に富んだ領域が残される。これを 炭素ポケット(carbon pocket) と呼ぶ。12C(α,γ)16O 反応率が最近の変更のように３倍になっても、C/O 核の組成は大きく変わるが、 炭素ポケットの組成には殆ど影響しない。この反応で C を O に変えるには時間が 足りないからである。図９に見られるように、炭素ポケットでは炭素が 20% から 25%, 酸素が 2%, 残りをヘリウムが占める。これは星のメタル量には依らない。 　図１０は 炭素ポケット先端での 16O の量である。 外層にあった CNO 元素の大部分( Z の 75%)は水素燃焼殻の後では 14N に変わっている。 熱パルスの結果、この 14N は 14N (α,γ) 　18F (e+ ν)18O で 18O になる。 しかし図１０にあるように、この 18O は、18O (α,γ) 22Ne で 22Ne に変わってしまう。低メタル星ほど 18O の低下が急だが、低メタルなほど熱パルスが強いせいである。 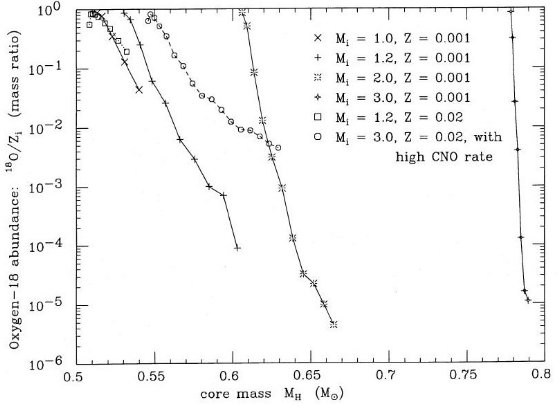図１０　熱パルス後の炭素ポケット先端での 初期組成に相対的な18O 組成。

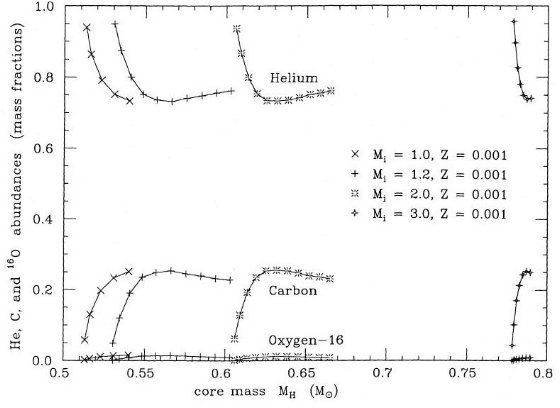図９a　熱パルス後の殻間組成。　Z = 0.001 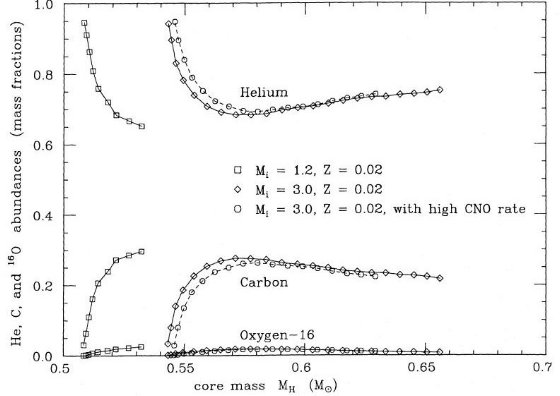図９b　熱パルス後の殻間組成。　Z = 0.02

vi) 核質量ー熱パルス間隔関係　 　Paczynski 1970 は、Y=0.27, Z=0.03に対して次のような関係を発見した。 　　log τif = 3.05 - 4.5 (MH - 1.0) = 4.5 (1.678 - MH)　　0.5 ≤ MH ≤ 1.4 　Wood,Zarro 1981 は、Y=0.30, Z=0.02 に対し、 　　log τif = 3.68 ( 1.914 - MH)　　　 0.6 ≤ MH ≤ 0.9 図１１は彼らの関係式が我々が Z = 0.02, Y = 0.27 で得た関係、 　　　log τif = 4.51 ( 1.689 - MH)　　　 0.5 ≤ MH ≤ 0.7 と合致することを示す。しかし、図１１は同時に、この関係が強いメタル量依存 を有することを示す。Z = 0.001, Y = 0.24 では 　　　log τif = 5.5 ( 1.54 - MH)　　　 0.5 ≤ MH ≤ 0.7 　低メタルになると同じ Mc で較べた時、パルス間隔は高メタルの２倍になる。

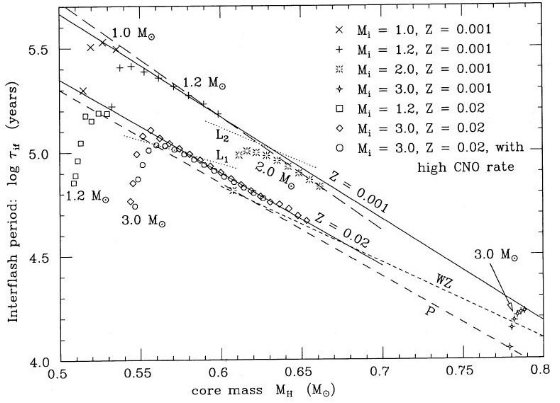図１１　Mc - τif 関係。