The Distribution of Dense HIIRs in the Inner Galaxy


Lockman
1979 ApJ 232, 761 - 781



　アブストラクト　

　濃い電波 HIIRs の分布を、円周回転の仮定と密度波理論を用いて、内側銀河 100° で定めた。北銀河系 l = [5, 55] の電波星雲は、南銀河系 l = [305, 355] の電波星雲に比べると、可視でも見える場合が２倍である。これは 遮光物質との関係で上手い配置になっているからであろう。南星雲は銀河中心 から 3 kpc 以内で見つかっている。北星雲は R = 4 kpc にまでしか迫っていない。 　濃い HIIRs のスケール高はどんな天体よりも小さい。平均高度の周りの z 分布分散度は僅かに 33 pc である。観測された銀経と視線速度から、運動学 モデルを作ると星雲が狭い幅に集中する。その形は２本渦状腕に似る。 この結果は星雲の運動学の詳細には依らない。 HI や 分子雲が沢山ある広い 領域に濃い星雲がないことは、大質量星の形成は分子雲の存在だけからは 言えないことを意味する。何か追加のファクターが必要らしい。Ro=10kpc

　２．運動距離の決定とその限界　

　回転曲線　

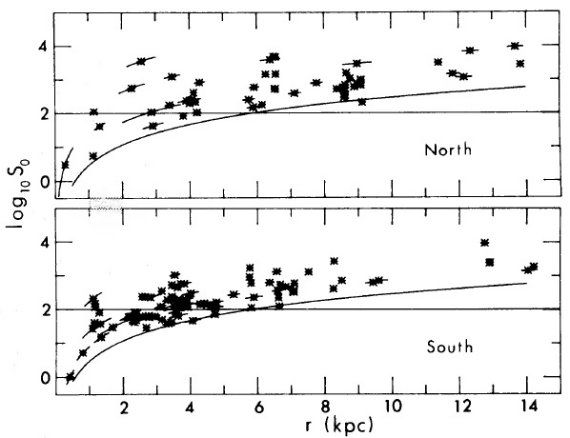
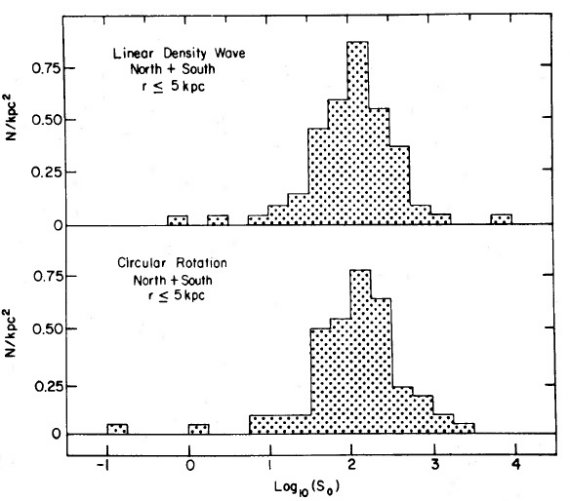
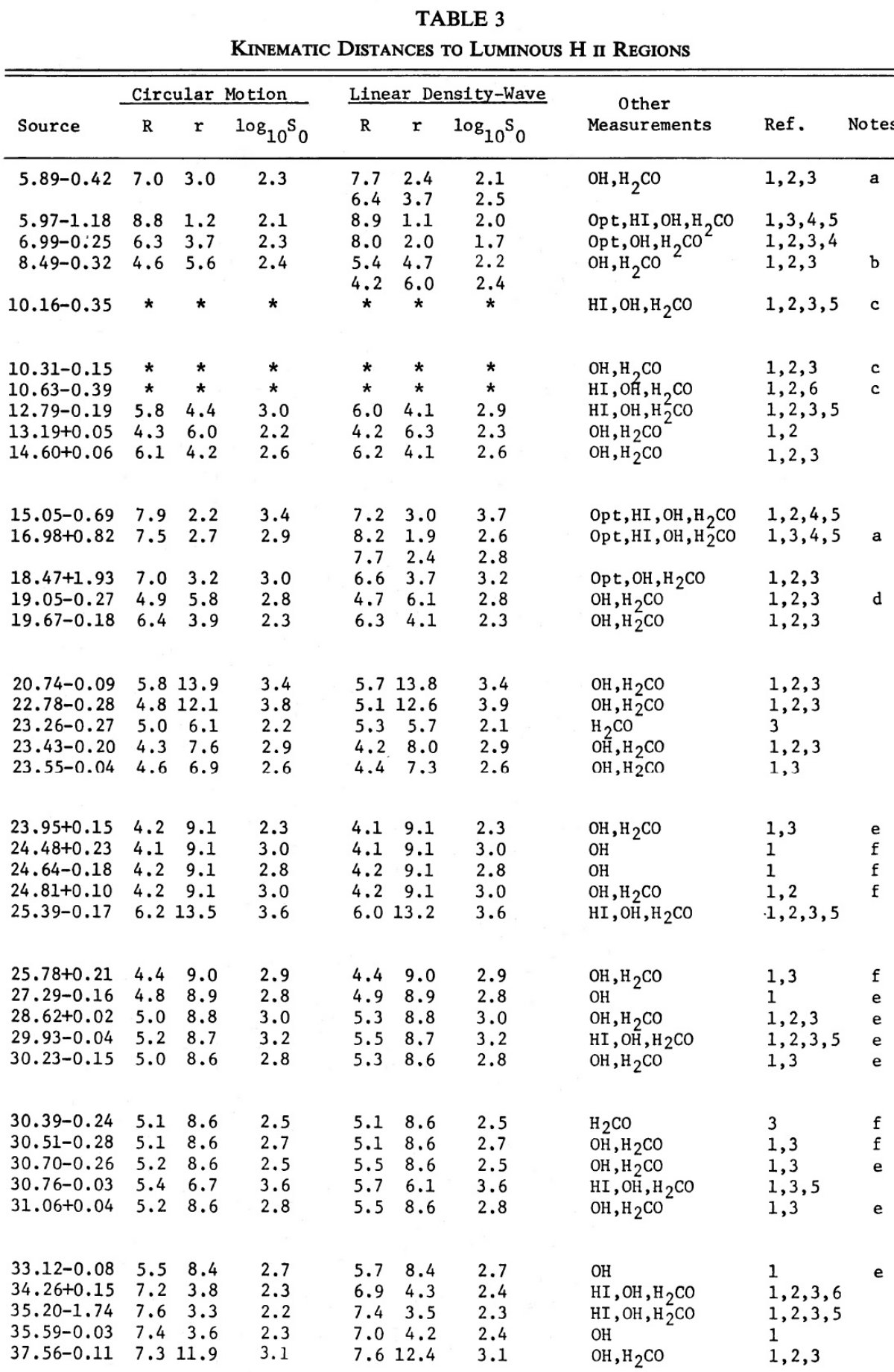
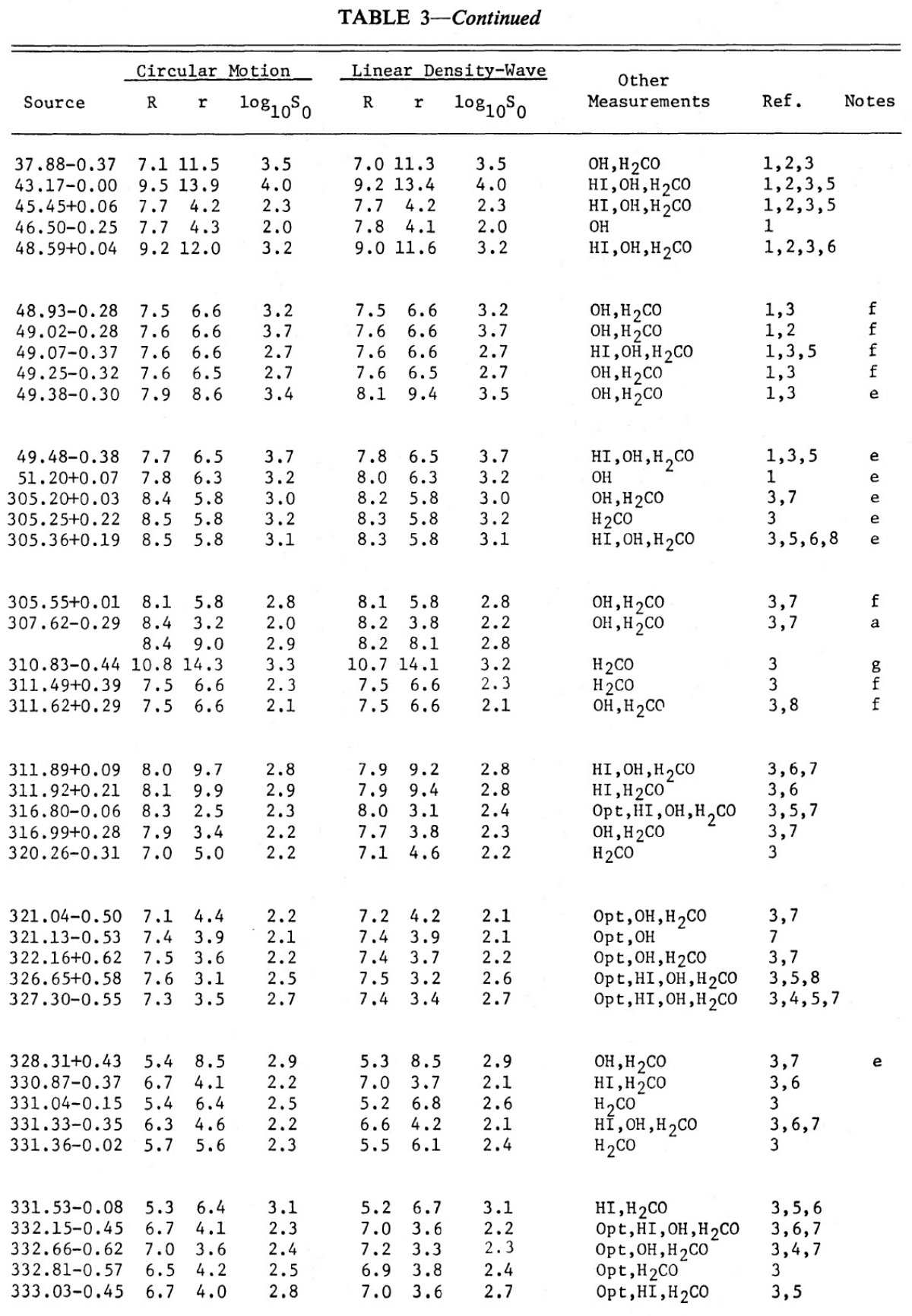
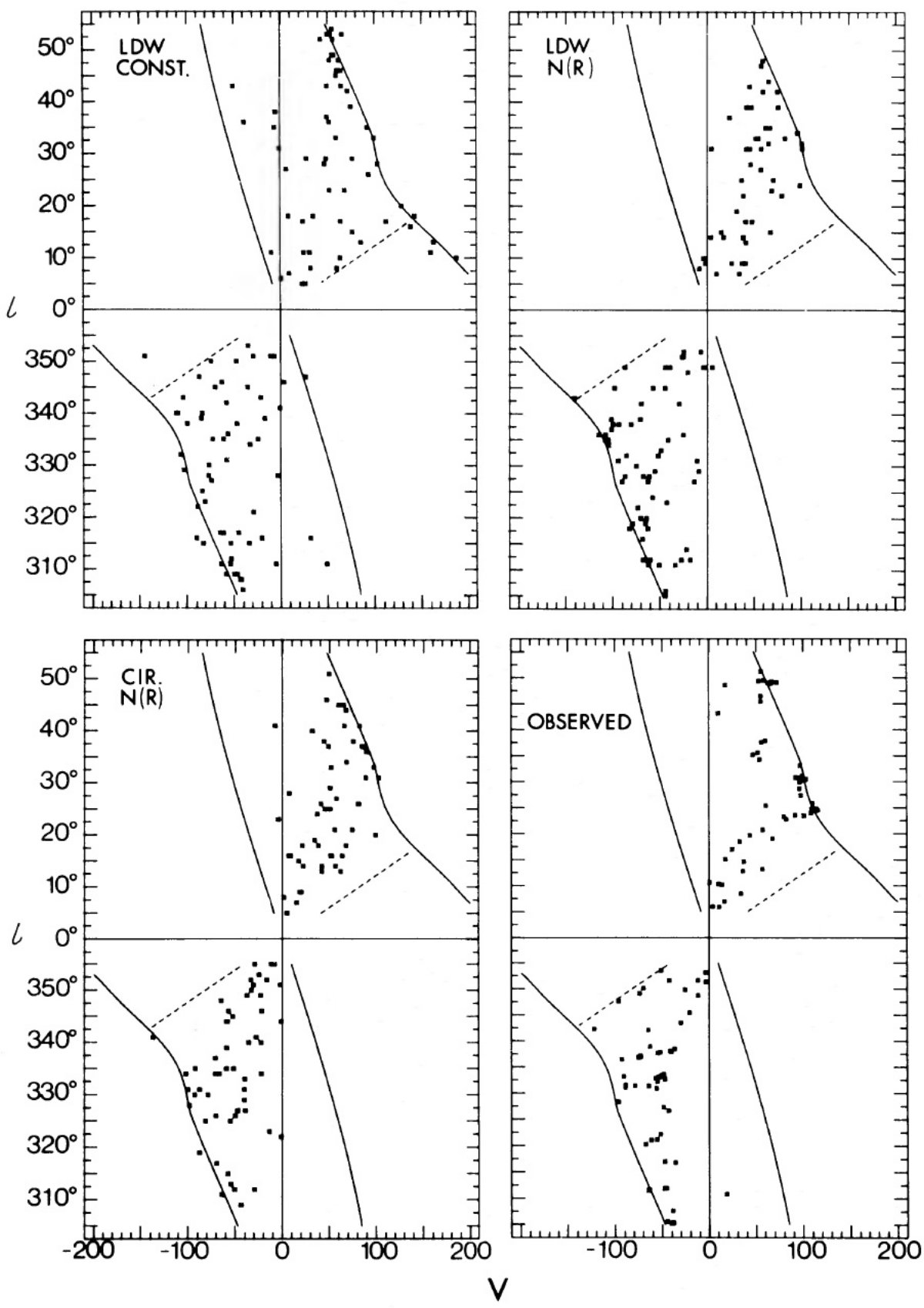
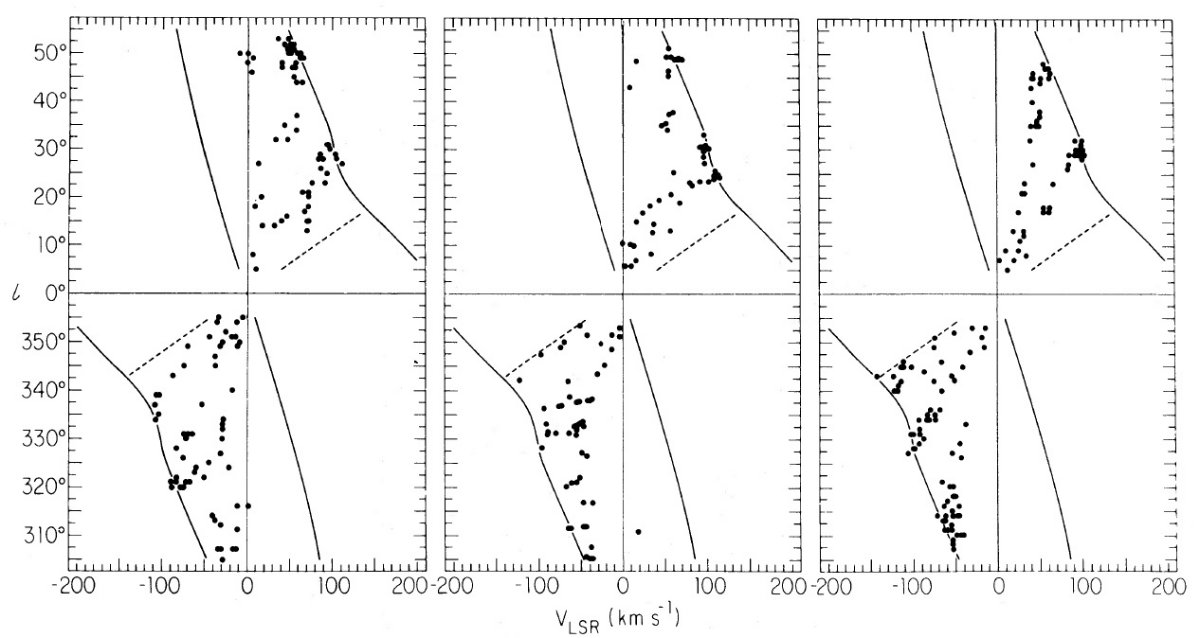
(i) R ≤ 5.5 kpc
　　Simonson, Mader 1973 を採用

(ii) R ≤ 5.5 kpc
　　 Burton (1971) が Schmidt 1965 の回転曲線を近似したものを採用。

(iii) ストリーミング
　　密度波理論は、動径方向と角度方向の摂動速度= ストリーミングが回転 運動の上に乗ることが予想する。線形近似でのストリーミングの性質は Burton (1971) が北銀河 HI スペクトルから導いた。非線形密度波理論はまだ応用に使うには 初歩的段階だが、濃い雲の運動には非線形効果は効かない。太陽近傍の腕間 空間の衝撃波については Shu 1072 のパラメタ―を使用する。ポテンシャル 極小位置は Burton (1971) のまま使用する。

(iv) R < 3 kpc
密度波とそれに伴うストリーミングは内側 R ∼ 4 kpc で消えるので、 R < 3 kpc では完全な円周運動を仮定する。この 3 kpc という値は 4 kpc 以下である限り結果にあまり効かない。

　遠・近運動距離の分離　

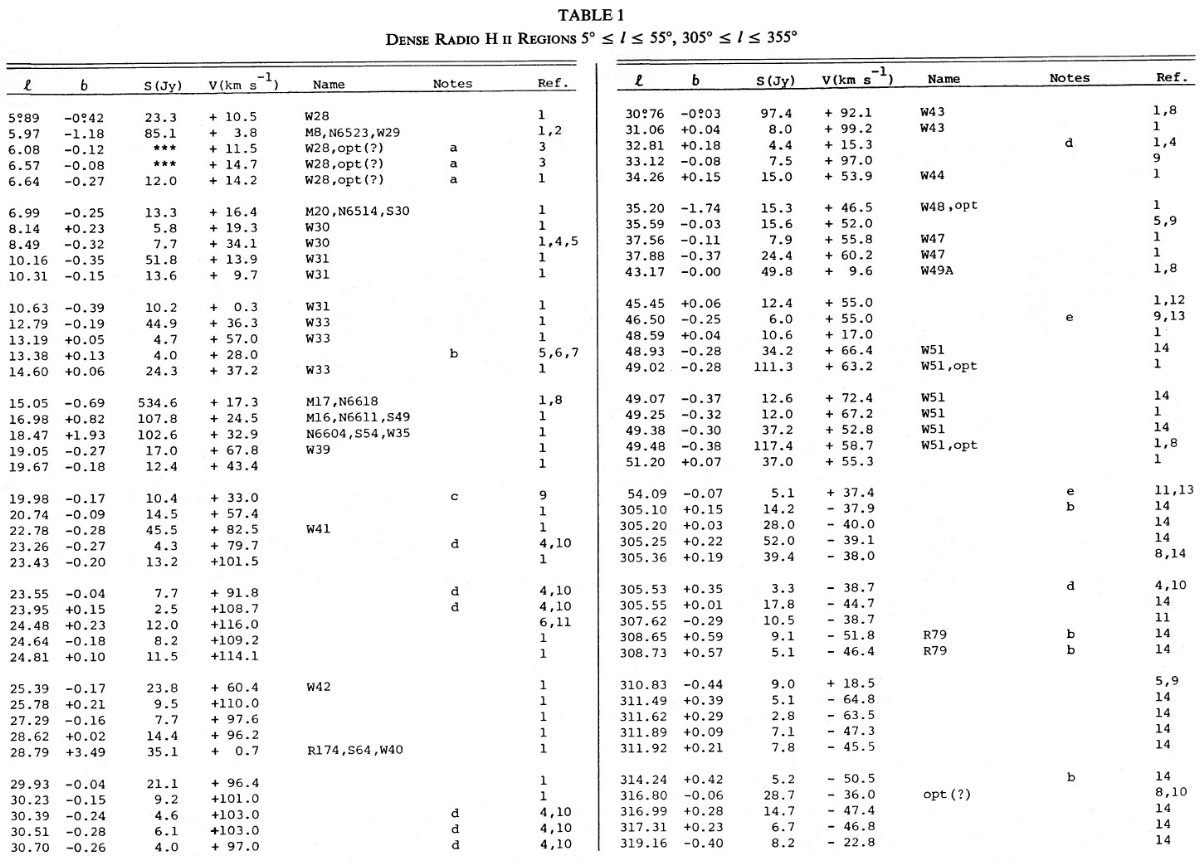
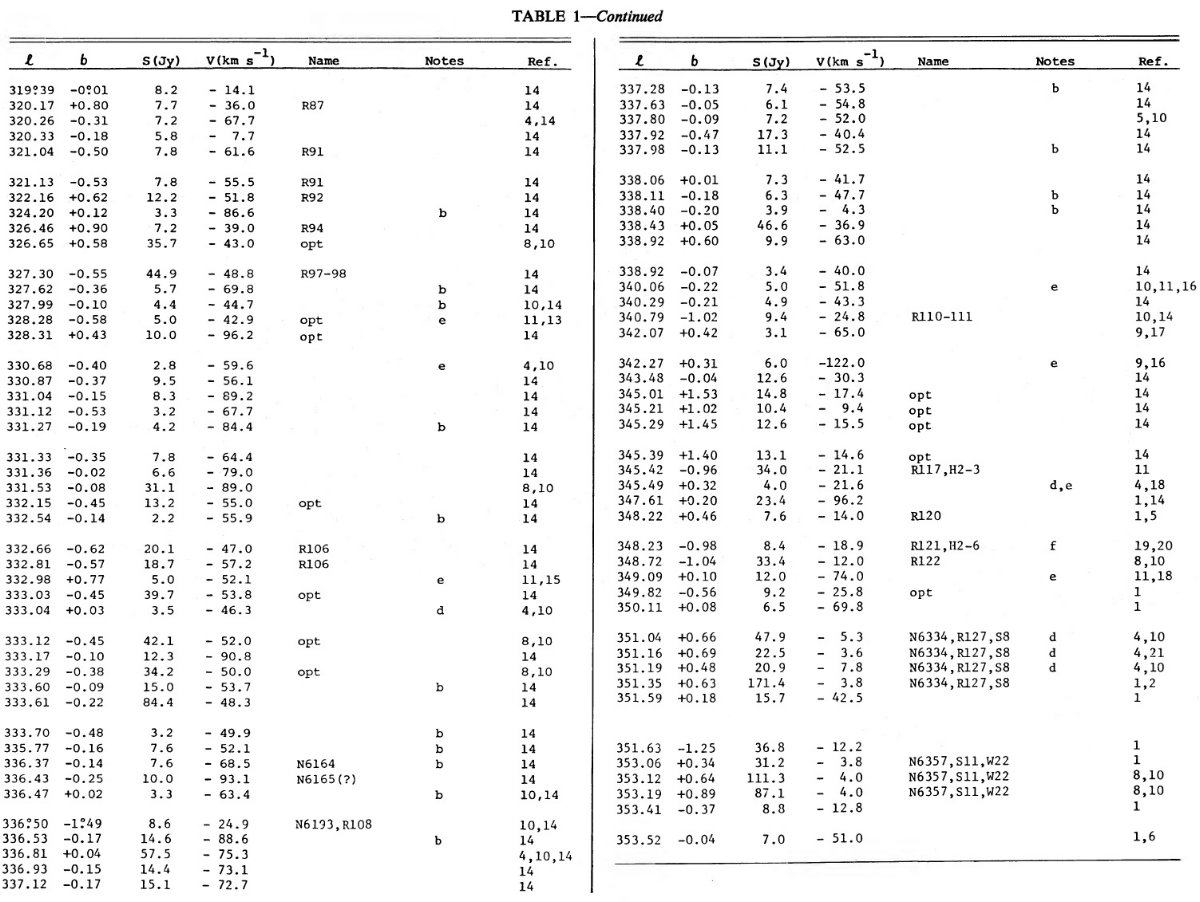
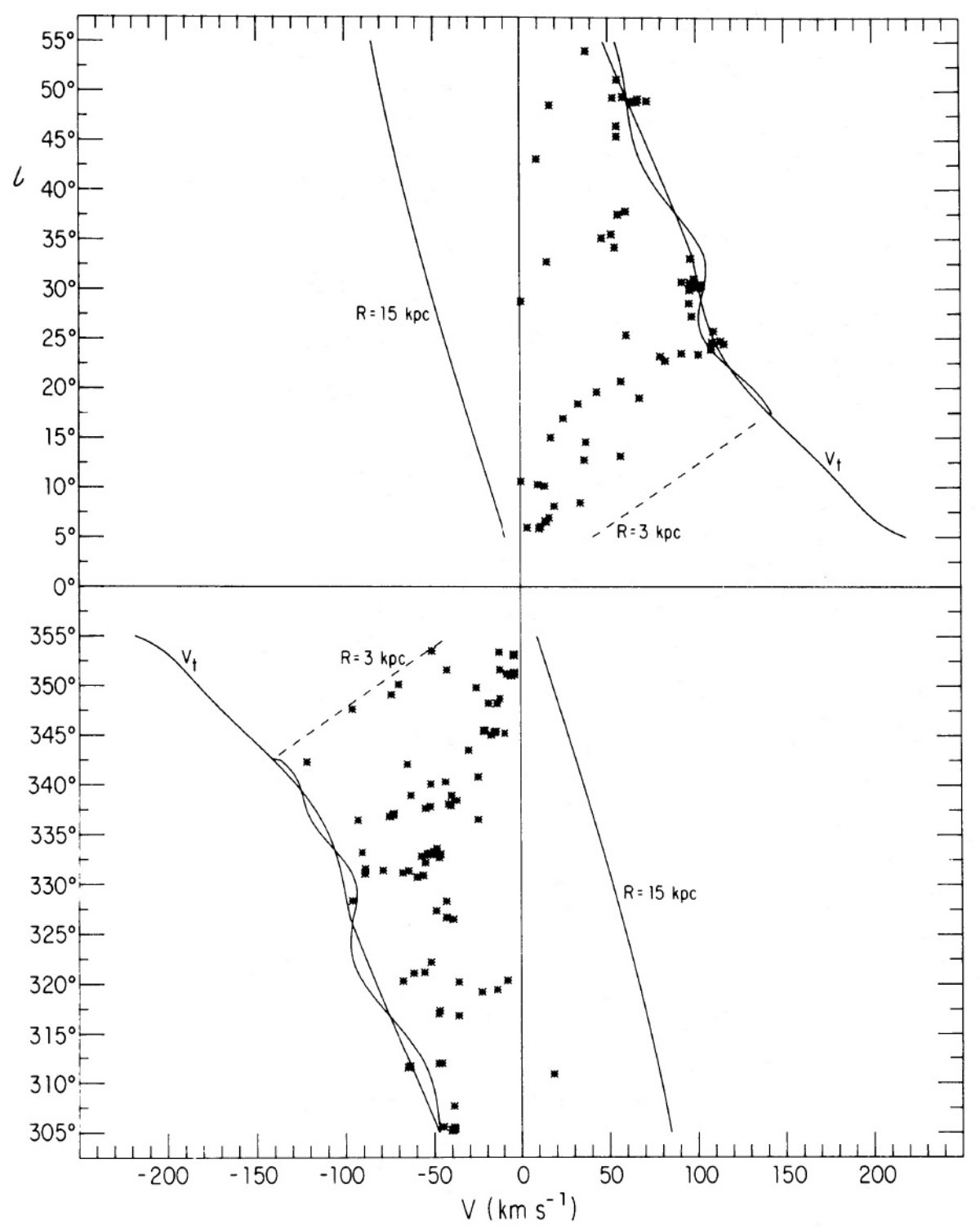
　幾つかの星雲は視線方向に対して可能最大速度位置にあり、従ってその距離 は R = Ro cos l に決まる。しかし、 R < Ro では通常二つの運動距離が 可能である。その区別には、星雲連続光に対する分子、原子吸収線が用いら れる。もし吸収線分布が Vt まで伸び、|V(HII)| < |Vt| なら、星雲は遠 運動距離にある。|V(abs)| ≤ |V(HII)| なら近運動距離である。密度波スト リーミングは V(r) の形を変形するので、候補距離が二つ以上になる場合が あるが、そう多くはない。

　HIIR のランダム速度とガス膨張速度　

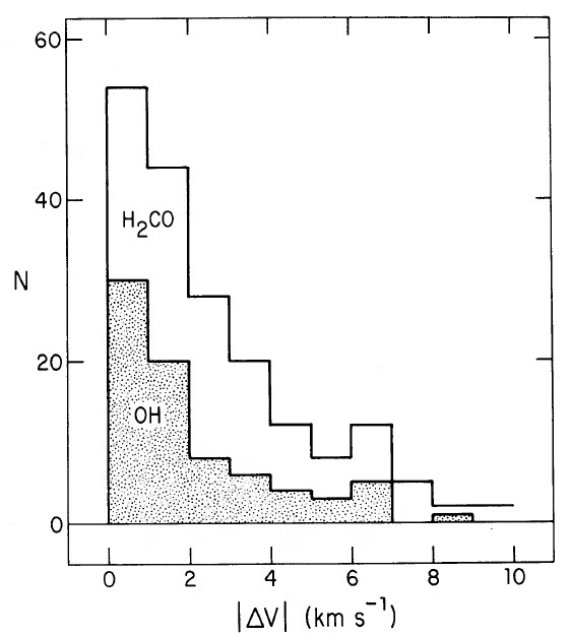
　HIIR を生み出しそうな雲のランダム速度と　HI ガスから離れていくガス膨 張速度も考慮すべき要素である。濃い雲のランダム速度は 4 km/s (Burton, Gordon 1978) である。Orion A で観測された膨張速度は 10 km/s であるが、 雲のサーベイからは、それほどの例は見つからない。そこで、両者の結合効果 は 5 km/s と考える。

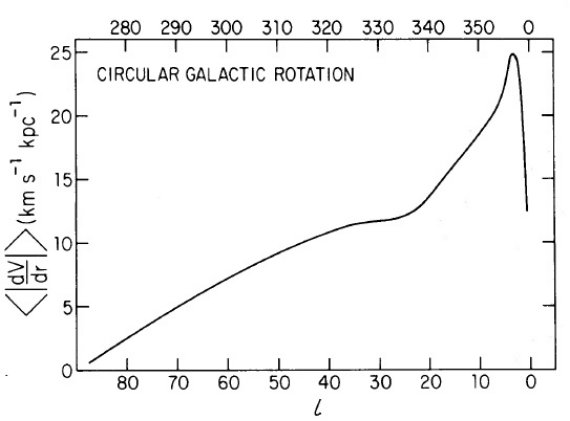
図１．円周運動に対する dV(r)/dr の視線上、太陽周円内部での平均値。 この量の逆数＝運動距離決定の不定性。

　速度場のエラー　

　太陽周円の外側の回転速度はよく決まっていない。そこで l = [90, 270] の方向は今回扱わない。太陽周円内側では銀河系速度場はストリーミング速度 の 8 km/s 程度のエラーを含むと考える。このエラーはランダムと言うより、 系統的なものである。

　距離決定精度 = dV(r)/dr　

　運動距離の精度は |dV(r)/dr| に比例する。大雑把な平均精度と銀経との 関係を図１に示す。 l = 70 ではランダム速度 5 km/s が生み出す距離不定性 は平均 1 kpc くらいであることがわかる。 l = [5, 55], [305, 355] の 不定性は小さいので、本論文ではこの区間を扱う。こうしても、まだ不定性は 大きい。|dV(r)/dr| が大きい箇所では HIIRs が存在しなかったりするからで ある。 R < 3 kpc のような空白域を除くと、 |l| = [5, 55] 区間での平均 運動距離不定性は 100 pc/(km/s) 程度である。速度の方の不定性（観測精度は 十分高いとして）を 10 km/s とすると、距離の平均不定性は 1 kpc となる。

　表１．濃い電波 HIIRs l = [5, 55], [305, 355]　









図２．H109α 再結合線サーベイ天体の FWHM Δv とラインピーク 温度 TL の関係。上＝ CSIRO. 下＝NRAO.印は観測者別。

　３．濃い電波 HIIRs サンプル　

　３．１．全サンプル　

　|l| = [5, 55] には、H109α が検出された連続電波源が 166 ある。 それらを表１に示す。可視対応天体があるものは、第５列に名前を載せた。 Westerhout 1958 サーベイの W 番号を載せたものもある。各電波源にいくつ の HIIRs が付随するかは不明である。熱連続波源は例えば RCW 106 のように 数個の放射源に分解され、異なる視線速度を示す。それらを個々の天体として 数えるか、まとめるかは簡便さの問題である。ここでは、登録天体を一個と して扱う。

　３．２．運動サンプル　

　図２には Wilson et al. (1970) の H109α ラインサーベイから採った、ライン巾とピーク高の関係を 示す。多くの弱いラインの幅が大きい。それらは距離不定性が大きい。 そこで、TL < 0.10 K の天体は運動距離決定から排除した。 さらに、TL = [0.10, 0.15] K, Δv > 40 km/s の 天体も除く。こうして 24 天体がリストから外された。

　４．観測的性質　

　４．１．銀経分布　


図３．濃い H109α 検出 HIIRs の &Delta:l = 3° での、積分連続光 フラックスと天体数の銀経変化。

　図３には、銀経３度巾内での HIIRs 数と平均連続光フラックス密度を示す。 どちらも、GC 方向に増加傾向を示す。星雲の 63 % は南銀河にある。これは 北銀河(140' 望遠鏡）で単一に見える天体でも、南銀河(210' 望遠鏡）で見る と幾つかに分解されるためかも知れない。しかし、それだけでなく、南銀河 には明らかに弱いHIIRｓが多い。
　分子雲、OH/IR 星、パルサーのような早期型天体の銀経分布は、濃い HIIRs よりも中心集中度が強い。

　４．２．銀緯分布　


図４．濃い H109α 検出 HIIRs の &Delta:l = 3° での、積分連続光 フラックスと天体数の銀緯変化。

　４．３．可視対応天体　

　可視位置と電波位置が一致し、 Hα と H109α 速度が 近い場合に可視同定とするが、新しく検出された弱い電波源に対して そのチェックはあまりなされていない。同定された星雲の 75 % は南銀河に 属する。南銀河の減光は北銀河に比べるとかなり弱いことが影響している かも知れない。

　４．４．分子雲との随伴　

　HIIRs に付随する分子雲は OH, H2CO の吸収線として検出され る。図５に、二本の線に対する速度差の分布を示す。

　４．５．v-l 図　

　図６には、H109α ラインを伴う HIIRs の l-v 図を示す。終端速度 Vt 近くの HIIRs が |l| = [35, 50] には一つもない。Vt に沿ってのこのような ギャップは HI, CO, OH/IR星の分布には見られない。星雲の分布は l = 0 に 対して対称であるが、 南銀河 R = 3 kpc ラインに沿った HIIRs の分布が 興味を引く。北銀河には似た特徴がない。

　４．６．まとめ　

　このような濃い HIIRs の観測的性質を表２に示す。

図５．分子吸収線を伴う星雲の数と、電離線と分子線の速度差、との関係。 OH と H2CO の両方が検出された星雲は図中２回現れる。




図６．H109α ラインを伴う HIIRs の l-v 図。実線＝円運動＋線形密度波 理論によるモデル終端速度。R=15 実線はそのモデルでの予想ライン。破線＝ 円運動仮定での R = 3 kpc 予想ライン。




表２．電波 HIIRs の観測的性質

　５．運動距離とその性質　


図７．絶対フラックス密度と太陽からの距離の関係。距離は円運動距離と LDW 距離との平均値。

　５．１．運動距離の導出　

　V(H109α) ∼ Vt の場合、遠距離と近距離の差は星雲のランダム 速度の範囲内に収まる。そこで、|V(H109α) - Vt| < 7.5 km/s の時には星雲は接点いちにあるとした。

　５．２．So(r) と N(So)　

　図７は So = 絶対フラックス密度と r = 太陽からの距離の関係を示す。 So = S(5GHz) r2 Jy kpc2 である。図の実線は So = 3 r2 Jy kpc2 の検出限界を示す。 南銀河には So < 100 Jy kpc2 の星雲が北銀河より多い。 それが南銀河で HIIRs の数が多い原因となっている。So > 100 に 限ると南北間の差は消える。

図８．太陽から 5 kpc 以内にある HIIRs の光度関数。上：円運動＋LDW。 下：円運動。

　図８に、太陽から 5 kpc 以内にある HIIRs の光度関数を示す。So < 100 Jy kpc2 で N(So) が低下するのは多分検出の不完全性の影響 であろう。So = 100 は O 型星に相当する。光度関数のメディアンがこの付近で あり、サンプルの半数は O-型星で励起されていることを意味する。r & gt; 5 kpc では、So > 100 の HIIRs しか検出されない。表３にはそれらの固有光度大の 天体をリストした。








表３．明るい HIIRs の観測的性質


図９．So > 100 の明るい HIIRs の動径分布。N(R) = 表面密度。
(So(R)の定義は良く分からない。 )

　４．３．動径分布　

　図９には明るい HIIR 表面密度の動径 R 分布を示す。 R < 3 kpc と R > 11 kpc には明るい HIIRs が存在しない。N(R) のピークは R = 5 kpc と 7.5 kpc にある。第２ピークは Mezger (1970) により最初に注意された。 図９には 表面光度密度 So(R) の分布も示すが、
(So(R) は意味不明。 )
なので省略。

図１０． So > 100 の明るい HIIRs の銀河面からの光度 z と銀河中心距離 R の関係。丸＝北銀河天体。三角＝南銀河天体。LDW 距離使用。

　４．４．銀河面高度分布　

　図１０には、So > 100 の明るい HIIRs の銀河面からの光度 z と銀河中心 距離 R の関係を示す。




図１１．So > 100 の明るい電波 HIIRs の銀河面分布。上：円運動＋密度波 ストリームモデル。下：円運動。最小マークは So = [100,200], 最大は So = 800 以上.

　４．５．銀河面上の分布　

　図１１の銀河面上分布はランダムではないが、はっきりしたパタ ーンも見えない。これは決して意外な結果ではない。仮に全ての HIIRs が狭い 帯の上に並んでいたとしても、運動距離の不定性のため、そのようなパターンを 認めることは難しいだろう。 　距離不定性は 1 kpc 程度もあり、１００点程度のサンプルが作るパターン は容易に破壊されてしまう。このように、モデルに依って、観測 l-v 図を 再現する方法で全体の構造を推定するべきなのである。




図１２．３つのモデルと観測 l-v 図の比較。左上：一様分布＋ LDW 理論モデ ル速度。右上：LDW で求めた表面分布＋ LDW 理論モデル速度。左下： LDW で求めた表面分布＋ 円運動モデル速度。右下：観測。実線：R=15 kpc. 破線：R=3kpc.　もう一つの実線； Vt 速度。

　６．運動学モデル　

　良いモデルは観測される l-v 図の主要な特徴を再現するはずである。特に、 モデルは観測図の一定銀経区間で、Vt付近に星雲が存在しないギャップ現象を 説明しなければいけない。 　どのモデルでも Vt 付近では速度が集中するので、星雲の存在確率は高くなる。 従って、観測されるある銀経区間での Vt ライン上の天体不在はモデルを区別 する大事な特徴となる。結論としてN(R)型の円対称分布からは、ギャップを作る ことはできない。つまり、 HIIRs は何らかの整列パターンを表している。 　図１３の渦状腕モデルはギャップを再現した。リングモデルは小さなピッチ角の 腕の近似としてもよいが、フィットを上げようとすると南北でリング半径を変える 必要があり、腕に接近してしまう。 結論として、観測 l-v 図のパターンは軸対称分布では説明できず、HIIRs が帯状に 並んだ配列と整合性が高い。



図１３．左： Burton (1971) の渦状腕構造に星雲を置いた時のモデル l-v 図。右：幾つかの同心円の上に 分布した場合。中央：観測 l-v 図。モデルは円運動を仮定。

　７．特異な速度を持つHIIRｓ　

　あんまり関係なさそう。