
表1.モデルで使用されたパラメタ―
| HI 第1象限観測の結果を、2種の銀河系速度場モデルにより、解釈する。 サジタリウス腕や他の主要腕に伴う大規模ストリーミング運動は円周回転の仮説 に基づく解釈を不十分なものにする。密度波理論から予言される速度場はより 満足のいく解釈を与える。この理論とさらに l-v 図に見える速度パターン、 終端速度の銀経変化に見られる系統的不規則性に基づくモデル I からはストリ ーミング速度 3 - 8 km/s が得られる。このモデルでは腕と腕間空間とでの密度 比は 3 : 1 で、渦状腕の傾きは 7° である。全体として観測への一致は良い。 | HI 密度分布と速度場は同時に決める必要がある。 スペクトルプロファイルは、密度分布の違いよりはストリーミング運動の違い の方に敏感に反応する。従って、速度場を密度分布に結びつける理論を使って 密度を決めなければいけない。密度波運動学に基づいてサジタリウス腕の銀河 系構造マップを作った。 |
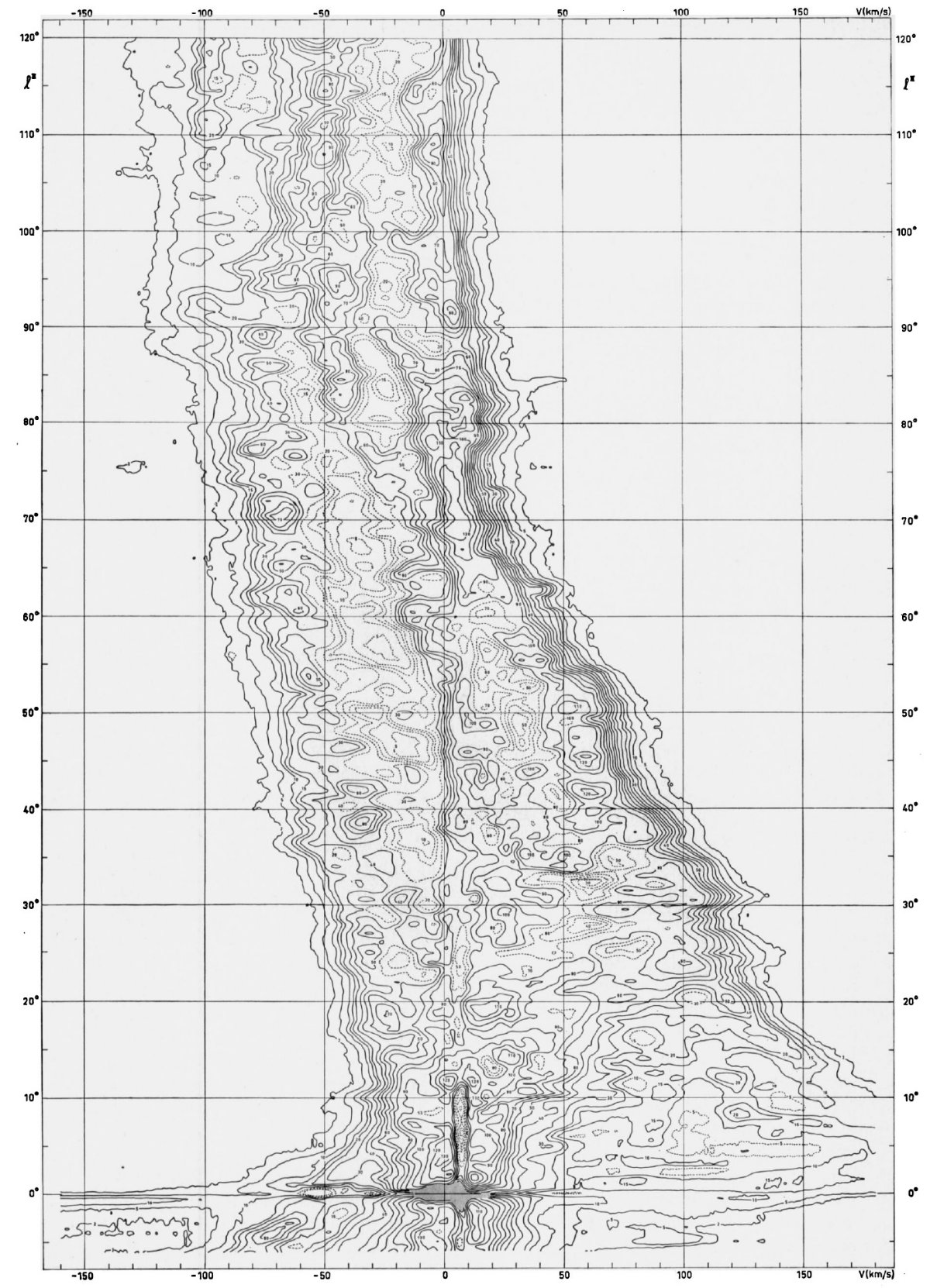
| オランダーオーストラリア HI マップの成功は円周運動を仮定して得られた。 しかし、 円周運動からの大規模な逸脱が明らかになってきた。速度場の不規則さ はそれだけで, 円周運動を仮定した解析から得られる HI 分布に渦状構造を生み 出すことが可能である。 そこで、幾つかのモデルを観測と較べた。モデルパラメタ―を表1に示す。 参照図として図1に l = [-6, 120] の観測結果を示す。 |
 表1.モデルで使用されたパラメタ― |
|
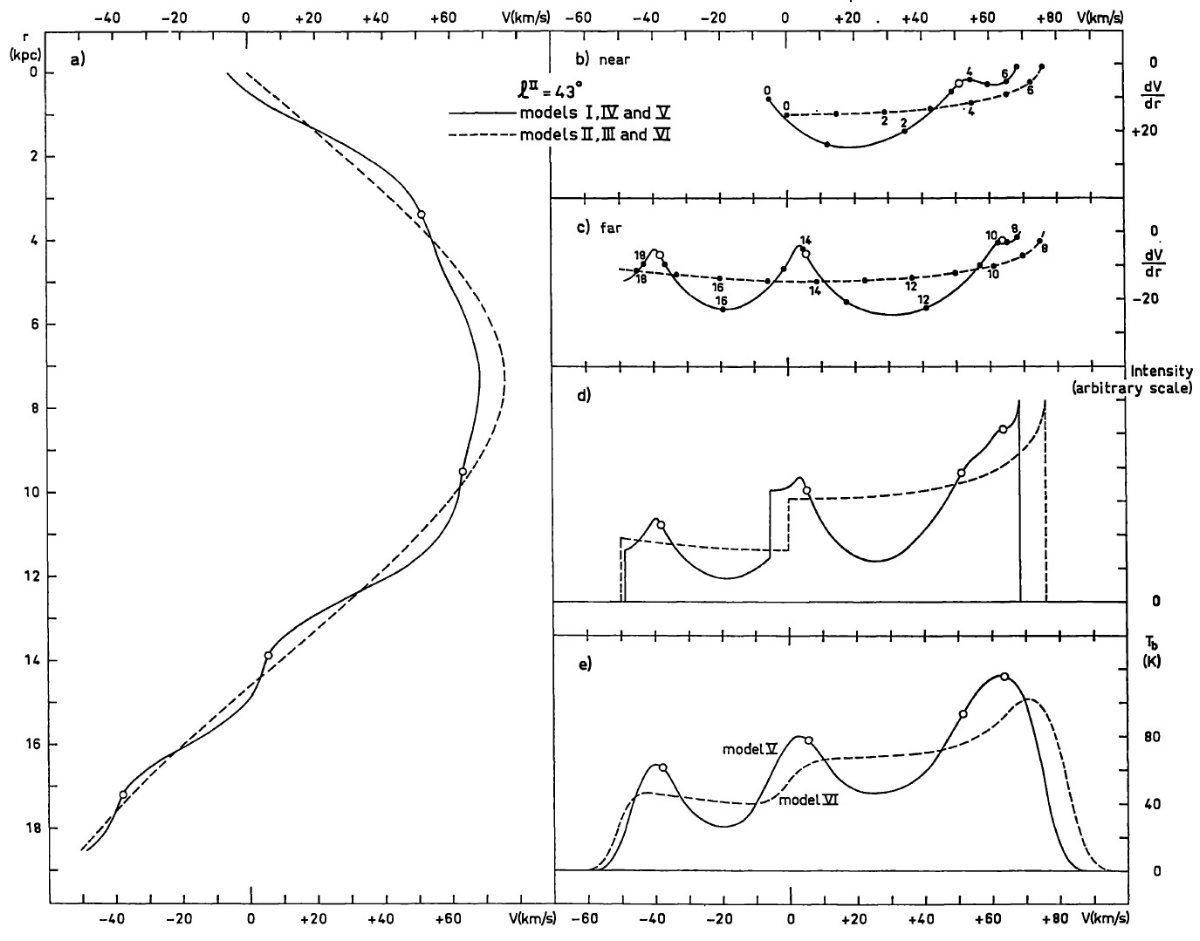
モデルに依存しない幾何学効果 第1象限で、まともな速度曲線に対しては、 (i) 接点効果 接点付近では距離に対する速度変化が小さい。ラインプロファイルとしては 高速度側の縁が切り立つ。 (ii) 遠近運動距離 視線速度正に対しては、視線上で少なくとも2点が寄与する。負速度に対しては 1点のみである。従って速度ゼロ付近で強度が落ちる。 |
系統的運動の効果 回転運動から系統にずれる運動があると、視線速度が距離に対して変化しない 点が現れることがある。 プロファイルへの効果 図2(d) では以上の効果をまとめて表示した。そこには速度極大に対応する 集中と速度ゼロでの不連続の両方が示されている。 |
| Lin et al 1069 の密度波理論から導かれるストリーミング運動の速度場を 与えているが略。 |
 |
 |
|
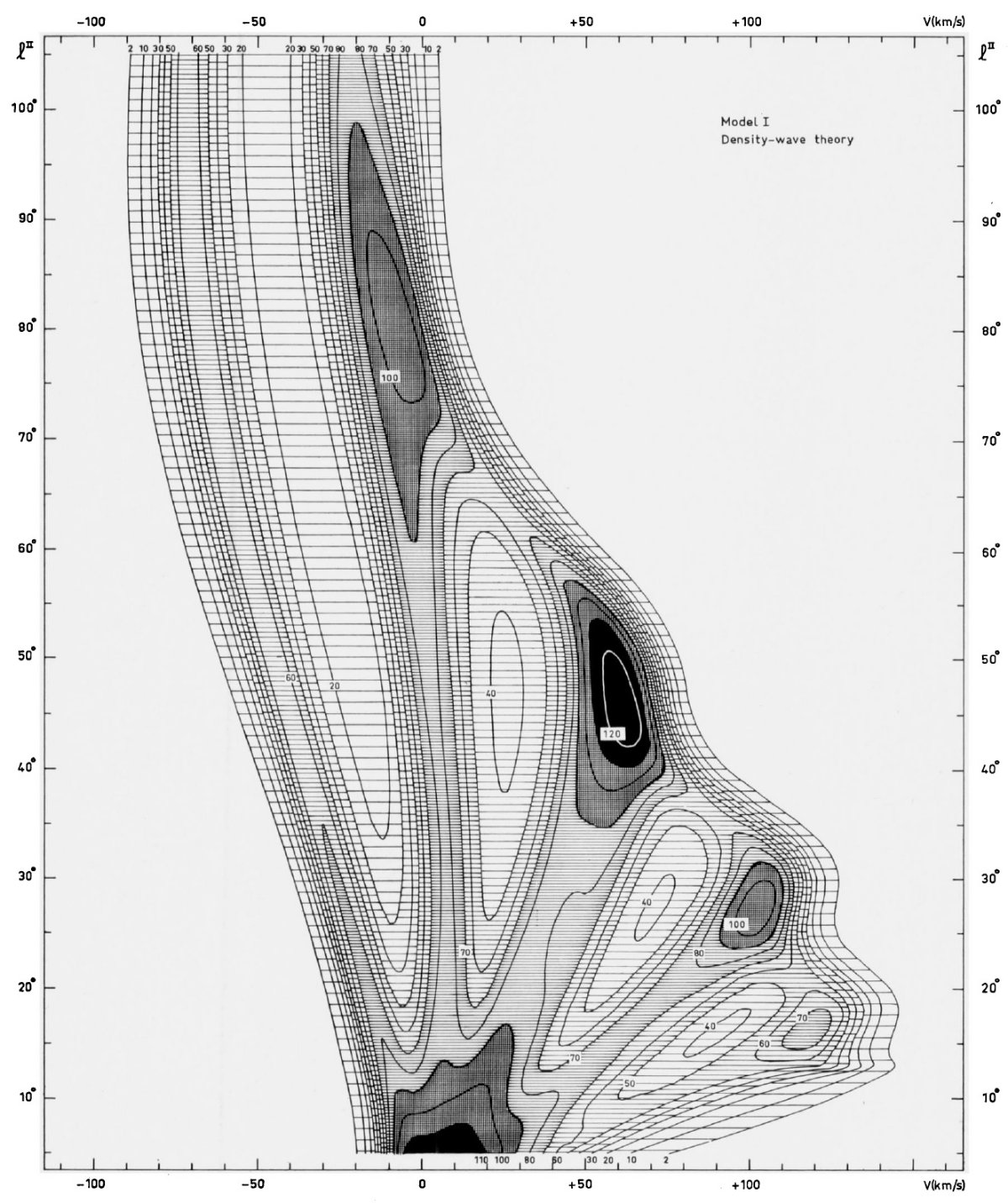
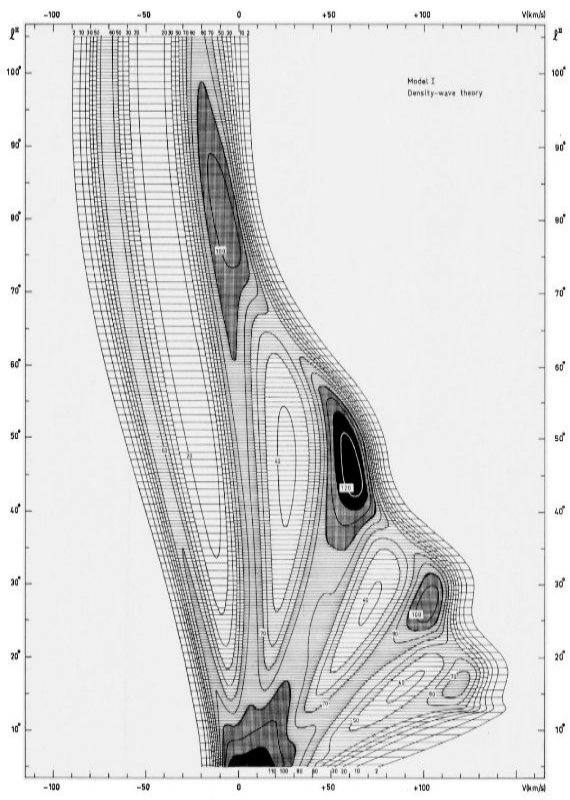
腕の配置 モデル I は1次の密度波理論から予言される特異速度に基づいている。 その結果は図4に表示され、図1(参照図)と比べられる。モデル計算のためには まず腕を配置する必要がある。 腕の一つを接点が l = 49 になるよう配置 する。これはサジタリウス腕のつもり。すると他の腕の位置はピッチ角のみで 決定される。ピッチ角の選択には lv 図上端末速度のコブ位置が使える。 l = 50° のコブはサジタリウス腕、l = 29° のコブはスキュータム腕 である。ピッチ角一定と仮定すると、コブ位置と等密度線の形は観測と合わなく なってしまう。それは主に他の腕が悪い位置に置かれるからである。それら、 他の腕は図1に示す観測 lv 図上で明らかである。ある程度連続な腕が第4象限 に見え、サジタリウス腕の外側の腕が速度ゼロ付近に、局所腕と重なって、 見える。放射極小の領域は極大領域と同じくらい観測結果の解釈にとって重要 である。負速度腕とゼロ速度腕と間の極小放射領域は図1(参照図)上、特に l = [30, 80] で、はっきり分かる。サジタリウス腕とゼロ速度腕との間の 極小放射領域も l = 50° V = 30 km/s 付近に見える。端末速度と分布図全体 の双方を合わせるには、ピッチ角 t と銀河中心距離 ω の間に tan(t) = t1ω + t0 と言う関係を仮定し、外側の腕では 円形に近くなるようにするとよい。ω = 5 kpc で t = 8°, ω = 10 kpc で t = 5° となるようにした。これは Lin et al 1969 の 「グランドデザイン」に非常に近い。 近い側の腕と遠い側の腕 ω < Ro = 10 kpc にある腕の稜線は lv 図上でループを作るが、 等高線間隔が大き過ぎ、速度分散により平滑化を受け、あとで述べる変形に よる平滑化のために、モデル l-v 等高線図で近い側の腕と遠い側の腕を分解 することは無理である。視線の幾何学効果により、稜線の接点より少し内側に 放射強度極大点が生じる。モデル I - V で、サジタリウス腕の外側にある二 本の腕は視線との交点は一つとなる。 コブ強度 ピッチ角が定まると、モデル腕終端速度でのコブ強度は、密度コントラスト ρmax/ρmin で決まる。モデルでは ρmin(ω=0 kpc) = 0.4 cm-3 から ρmin(ω=10 kpc) = 0.15 cm-3 に対応して、 ρmax(ω=0 kpc) = 0.4 cm-3 から ρmax(ω=10 kpc) = 0.65 cm-3 に変わる。 ω > 10 kpc では ρmax, ρmin の 双方とも ω=25 kpc でゼロとなるよう線形に減少する。従って、 ρmax/ρmin は ω=0 kpc で 0, ω ≥ 10 kpc で最大値 4.3 を取る。 ストリーミング振幅 ピッチ角と密度比をこうして決めると、ストリーミング振幅はモデル式を 使って決まる。その最大値は ω = 7 kpc で 8 km/s, 最小値はエピサイ クリック周波数 χ(ω,θ) = 5π と ω = 13 kpc でのカットオフ近くの 2.5 km/s である。図6にモデル I に対するストリー ミング振幅を示す。 |
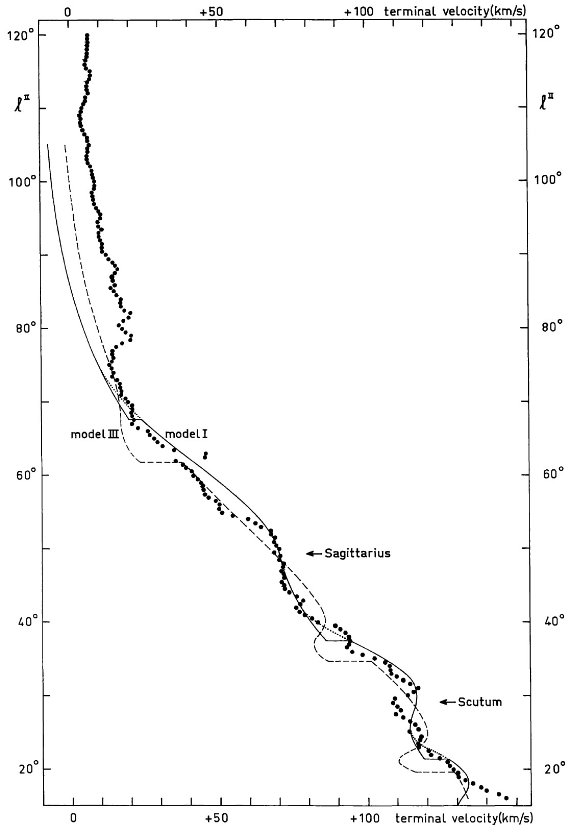
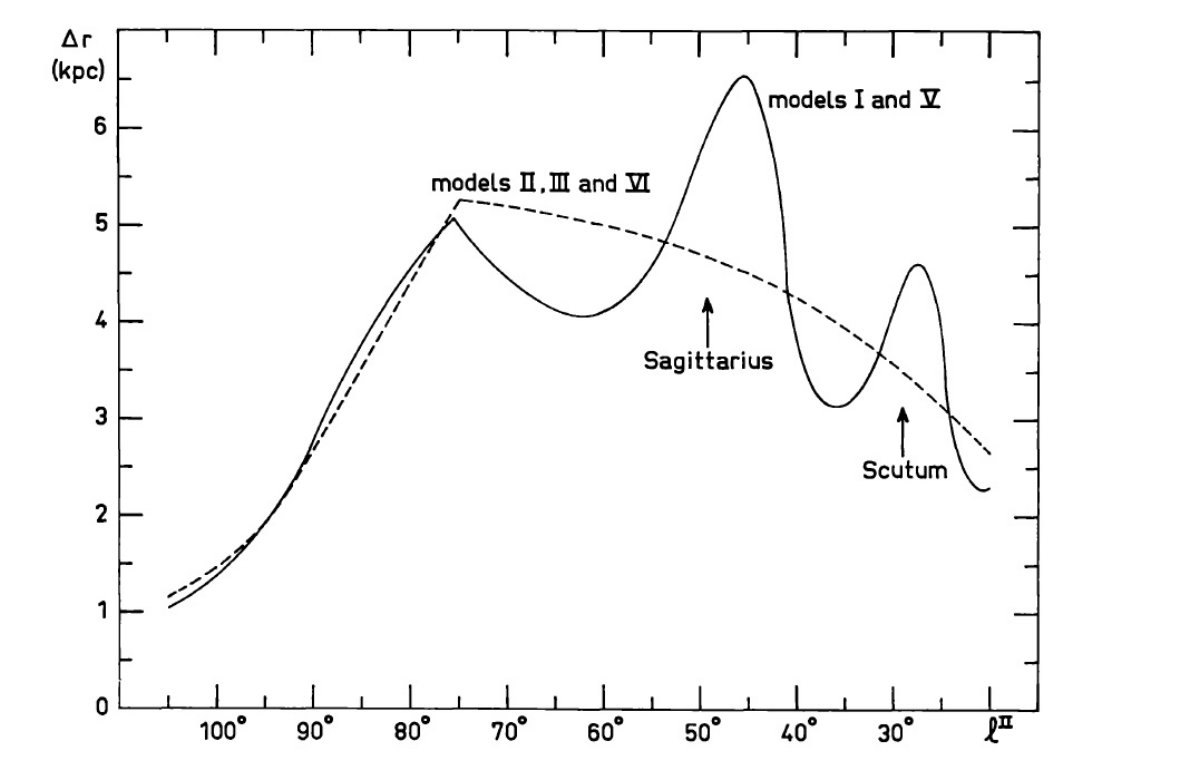
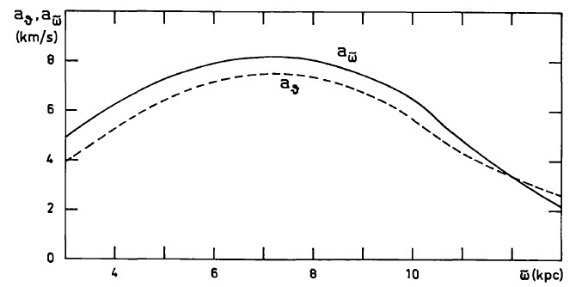 図6.密度波理論が予測する、モデル I, II, V での特異速度の動径方向成分 ω と 角度方向成分 θ の振幅 aω と aθ の銀河中心距離依存性。 終端速度 図5で終端速度を観測とモデルとで比較する。一致はかなり良い。モデルでは l = 30, 50 に終端速度のコブが生じるがこれは観測されるサジタリウス腕と スキュータム腕に対応する。一致が悪いのは l = 38 に現れる第2のコブで、 モデルには見えない。また、 l = 55 の観測は l が 1° 変わる間に 速度に 10 km/s の落下を示す。速度や密度の急激な変化は1次密度波理論では扱えない。 モデル I の l = 67, 38, 22 における終端速度の急落の原因は、落下の下側 の銀経では最高速度はある腕の外側の腕のガスからの寄与で決まり、一方落下 上側の銀経では最高速度は、次の腕の内側に沿っての反対向きのガスストリー ミングからの寄与で決るからである。 ("above", "below" を上訳のように 取ったが、意味不明の文章になった。イメージが全然掴めない。) 円周運動からのズレが存在する場合、観測される最高速度は必ずしも接点から来る とは限らない。 終端速度不規則性のフイット もしモデル I 計算を第4象限まで拡張すると、得られる終端速度不規則性はその 振幅においては南銀河の観測と合う。しかしその位置は合わない。銀河全体をパラメ ター表現するのは単純化のし過ぎと言うことを意味するのだろう。ω < 5 kpc の観測を説明することを考えたのがモデル IV でモデル I に膨張域を重ねた。 |
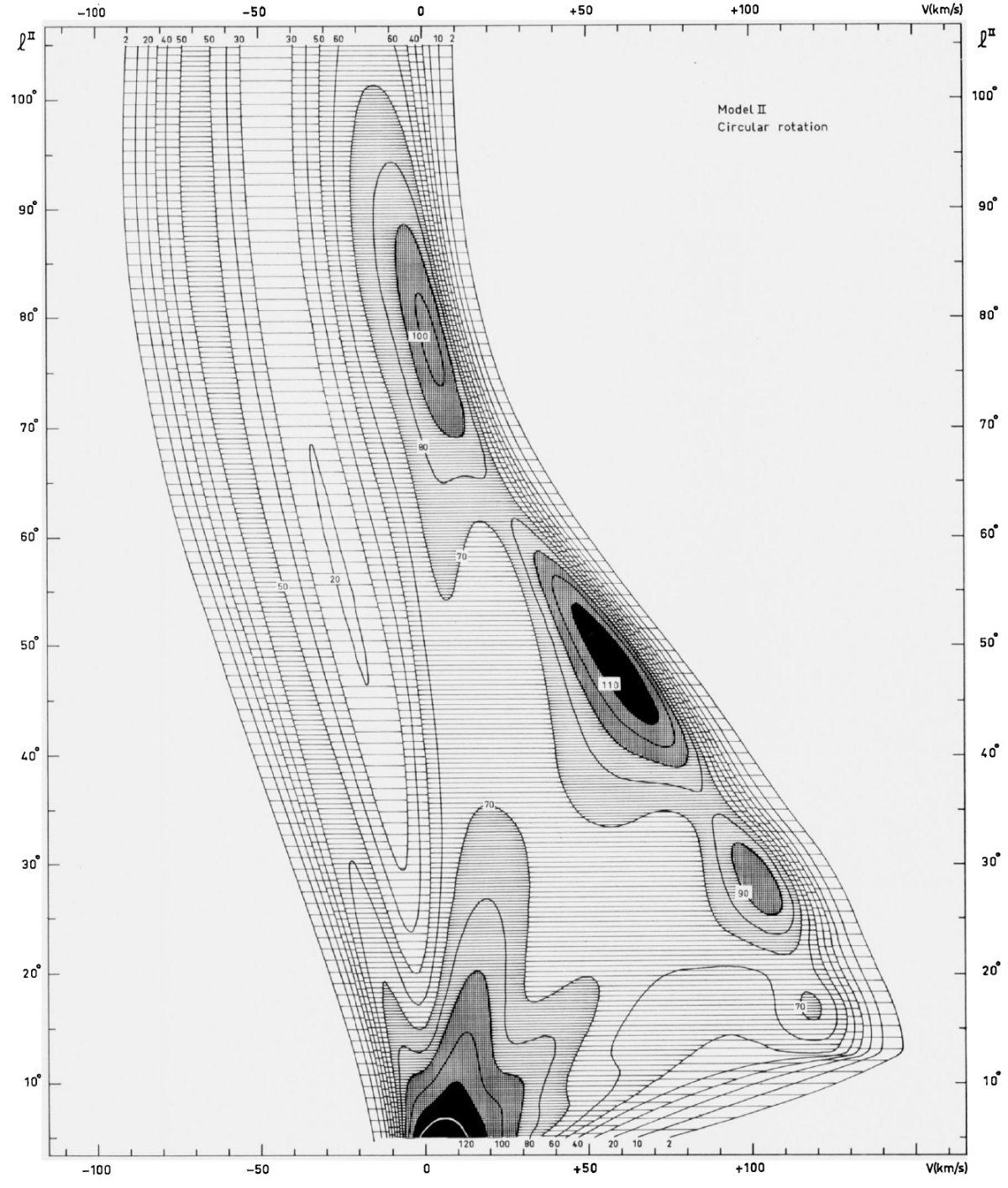
 図4_S.モデル I = 一次の密度波理論による、の lv - 等密度線。 |
 図7_S.モデル II = モデル I と同じ密度分布で円周運動を仮定した、の lv - 密度分布。 |
|
図7=ストリーミングによる lv 図の変化 適当な密度分布と円周運動に基づくモデルでは、モデル I ほど上手く観測 を再現できないことを示すため、モデル II, III を計算した。モデル II では 密度分布をモデル I と同じにし、回転曲線のみから速度場を得た。このモデル で得た密度分布を図7に示す。密度分布は共通であるが、lv 図は異なる。その 原因はストリーミングである。 |
図7のフィットは悪い モデル II の lv 図が観測に合わないことは明らかである。終端速度の銀経 による変化はなだらかである。しかし、観測ではサジタリウス腕の極大稜線は 銀経に対し殆ど等速度である。この特性はモデル I には現れているが、モデル II には現れない。 |
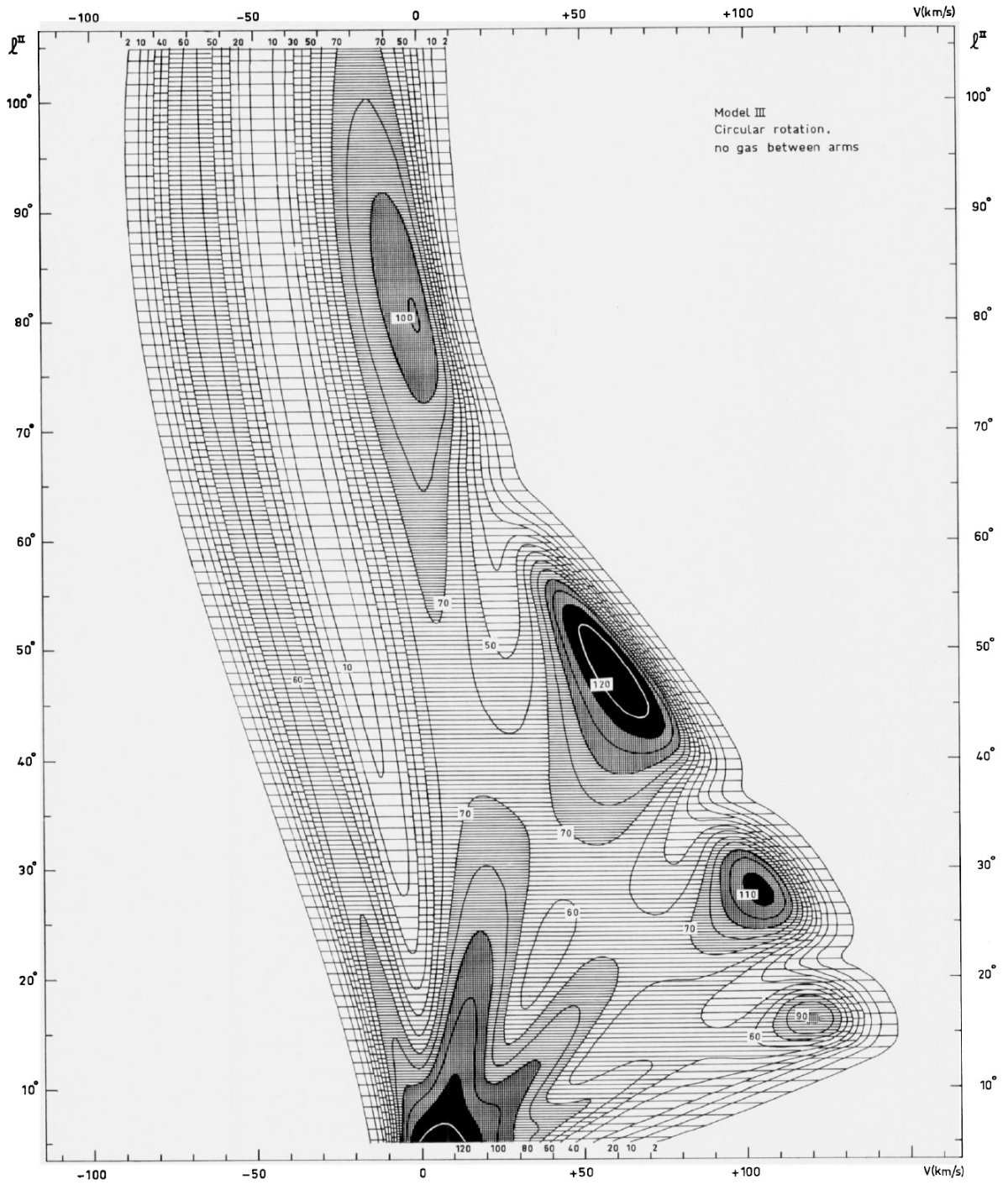
 図8_S.モデル III = 円周運動で腕間ガスなしの lv - 等密度線。 |
 図7_S.モデル II = モデル I と同じ密度分布で円周運動を仮定した、の lv - 密度分布。 |
|
図7=腕間でガス無しで lv 図のデコボコを作っても 密度分布を調整しても円周運動モデルではフィットを向上させられない。 モデル III では腕間空間にガスなしとして、円周回転モデルを作った。平均密度 ⟨nH⟩ の分布は以前のモデルと同じである。しかし、 モデル III では動径密度分布が正弦波関数的に変わり、腕稜線で 0.8 cm-3、腕間でゼロとなる。 (どう理解すれば良いのだろう? ) このモデルの終端速度は不規則性を示すが、観測とは異なる形である。図5に端末速度の 比較を示す。また、モデルでは高速度の l = 22, 36, 63 で低強度となる。しかし、 観測の特徴は極大速度の近くで強度が高まることなのである。 |
図7のフィットは悪い Shane, Bieger-Smith 1966 は腕間空間を空虚にするモデルを否定した。 その理由は、プロファイルの端の低強度の広がりが観測に見られないからである。 円周運動には非現実的な分布解しかない 円周運動モデルで終端速度の特徴をもっとも良く再現するには、 接点速度から 10 km/s 以内の速度に対応する領域のガスをなくして、プロファ イルの極大速度部分を下げるのがよい。これは図9から分かるように視線方向 で 4 - 5 kpc に及ぶ部分が水素無しになることを意味する。 |
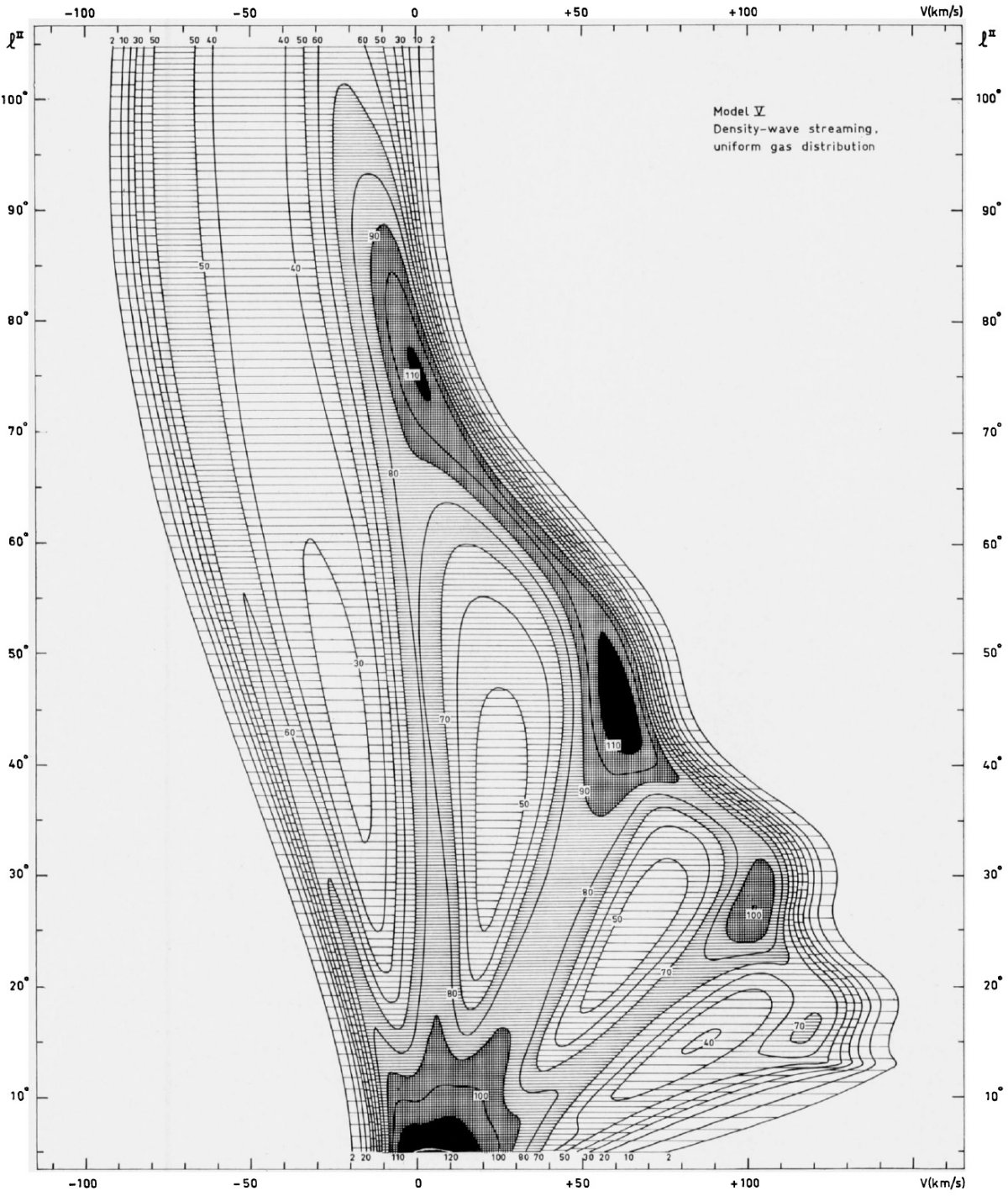

 図4_S.一次の密度波理論によるモデル I での等密度線。 |
 図10_S.モデル V = モデル I 速度場、一様密度の lv 図。 |
 図10_S.モデル V = モデル I 速度場、一様密度の lv 図。 |
 図11_S.モデル VI = 円周運動、一様密度、の l-v 図。 |
|
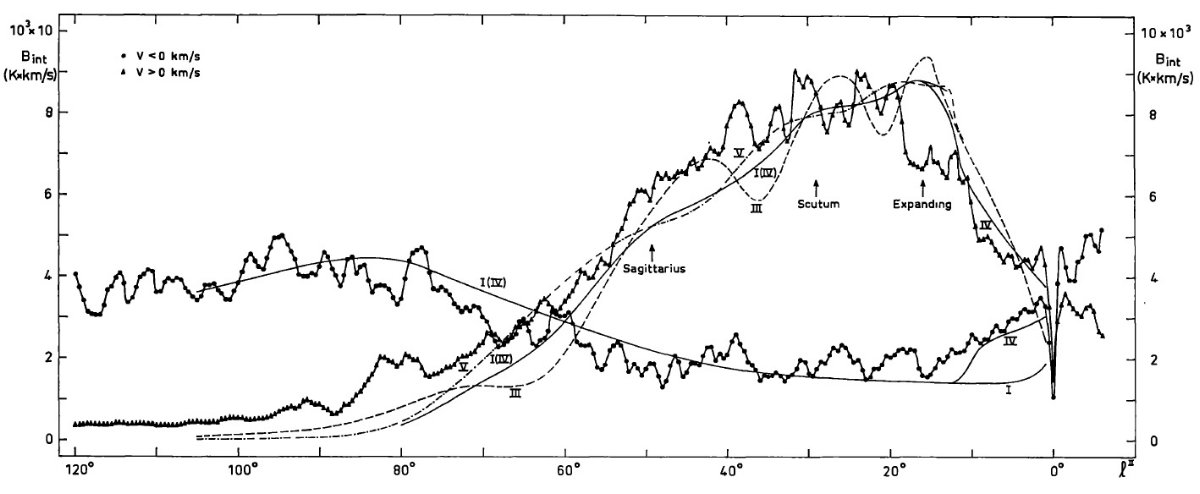
モデル V, VI は一様水素分布を仮定 モデル V, VI は一様水素分布を仮定し、幾何学効果とストリーミング効果 を調べるために作った。モデル V はモデル I の速度場と一様分布(nH = 0.4 cm-3 を仮定し、l = [5, 105] で計算した。モデル VI は 円周回転速度場と同じ一様分布を仮定した。図10、11にそれらの lv 図を 示す。モデル VI のパターンは完全にモデル非依存な効果である。モデル V のパターンはモデル非依存な効果に系統的な運動が加わって生じた。従って 両者の差は完全にストリーミングの効果である。 密度コントラストは lv 図に殆ど効果がない モデル I とモデル V の類似性から、モデル I の密度コントラストは lv 図 に殆ど効果がないことを意味する。 (では、lv-図からどうやって密度分布 を求められるのか? ) 両モデルの一般的なパターンは同じで、観測 lv 図はモデル I でもモデル V でも同じくらい良いフィットになる。 段差はストリーミング 面白いのはモデル V が比較した中で2番目にフィットが良かったことである。 光学的深さプロファイルの下の積分値はモデル V と VI とでは同じで、銀経に 対して段差はないが、モデル V の積分輝度温度には銀経に対し段差が生じる。 これらの図12に見られる段差は、一様密度であっても、ストリーミングによる プロファイルの総距離(速度分布の集中?)と光学的深さと輝度温度の非線形 効果の結果、生じるのである。 |
ストリーミングの強力な効果 モデル V は観測の解釈に当たって生じる問題を浮き上がらせる。勿論、モデ ル I の標準ストリーミングはモデル V の一様モデルより良い。それはモデル I の速度と密度が現実的で、自己無撞着であるからである。速度と密度は相互に 関連するので、lv 図の全体パターンがストリーミングの結果である場合でも 渦状の空間構造を描き出すことは可能である。それにも拘らず、モデル I と V の間での選択を正当化する情報はないことを示すのにモデル V は重要である。 モデル I に示すようなストリーミングが存在すること、その運動だけで 通常は渦状構造を意味すると考えられている観測を説明するのに十分なこと を理解するのは重要である。ストリーミングはプロファイルを完全に変えて しまうので、観測の解釈ではストリーミングの効果を考慮する必要がある。 ストリーミングを調整すると一様密度からどんなプロファイルも作り出せる。 密度波理論の正当性 密度波理論の正当性はまだモデルで実証されていないが、密度波理論の速度 場は円周運動より観測に良く合う。 |
|
思考実験 次の思考実験を考えよう: (i)簡単な、例えばモデル VI を考えよう。 (ii)論文II の方法でモデルラインプロファイルのガウシャン解析を行う。 (iii)患側 lv 図を導いたのと同じ方法で lv 図を作る。 (iv)lv パターンを逆変換して同じ仮定速度場で距離を導く。 最後に得た空間分布は最初の入力モデルと異なる。モデルから得たlv 図と 空間分布との間に一対一対応を仮定すると、実際には存在しない構造を生み出す。 l = 65 - 85 高速度稜線が間違いを生む 思考実験の結果を考えると、間違った構造に導く、最もはっきりした lv パターンは、モデル等高線マップ上 l = 65 - 85 に現れる高速度稜線である。 モデルと同様な盛り上がりは観測にも見える。図9に示したような速度集中 効果はどんな空間密度増加をもしのぐので、このような輻射増加を Weaver (1970) のように主要構造と看做すのは間違いである。 接点付近のループの特徴 低銀経帯にも高速稜線を構造と見誤る危険がある。一般に膨張腕と呼ばれる、 v = 135 km/s, l < 22° のパターンは、高速帯でよそうされる強度増強 を考慮する必要がある。同様に、論文 II で名付けられた l > 35 の構造 H は分離した構造と考えてはいけなくて、高速稜線の一部を形作る強度も盛りあがり と考えるべきである。この稜線が根強いので、渦状ループが特徴的な音叉型の構造 を示し、接線より先の銀経側まで伸びて行く。このようなループはサジタリウス腕 (論文 II の図4にある延長部AB)にもScutum 腕にもある。 |
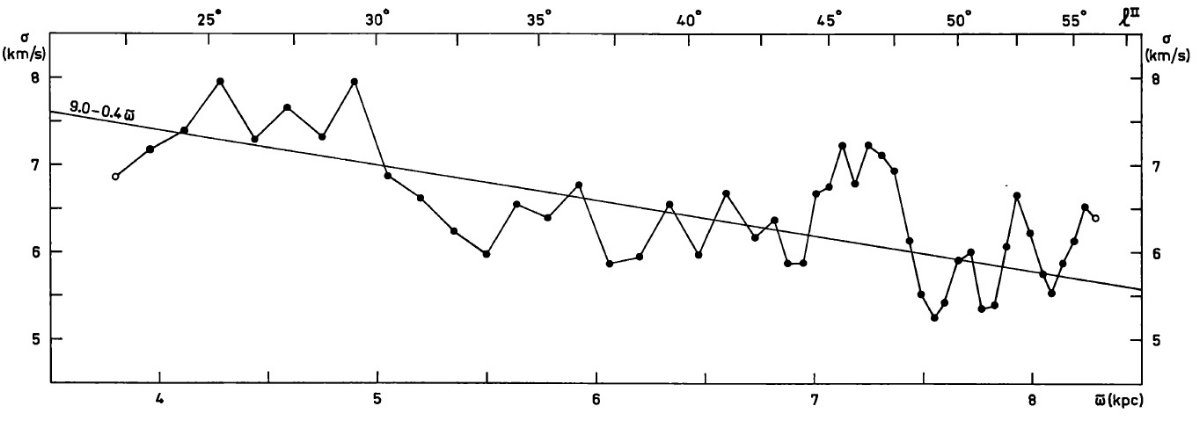
他にも誤解釈の危険 他にも誤解釈の危険があるパターンがある。高速稜線効果は lv 図でパターン を辿る時に注意しなければいけない。 Weaver (1970) の図7にあるような lv 図上の分枝は銀経で長く伸びている。このために Weaver (1970) が見出した遠近腕の間隔は我々の論文 II よりも大きい。これが、彼の得た ピッチ角が 12°.5 と大きいことを説明する。 ストリーミングと速度分散 もし図10,11のプロファイルがここで提案されように解析されたら、 結果としての分散は入力した分散とは異なる。モデル非依存効果が構造の広がり をもたらす。一方、非円周モデルでの巾はストリーミングに大きく影響される。 図9を見ると、ストリーミングがある場合、最高速度での光学深さが最も 大きくなるのは接線方向より少し手前である。モデル I , V で最高速に最大 の寄与が最高になるのはサジタリウス腕で l = 43° - 48°、スキュー タム腕で l = 25° - 30° である。同じ銀経では、図3にあるように 高速で観測される分散が最大になる。これは寄与する光路長が渦状腕の所で 大きくなるからである。 付いてけない この先限界。 |
|
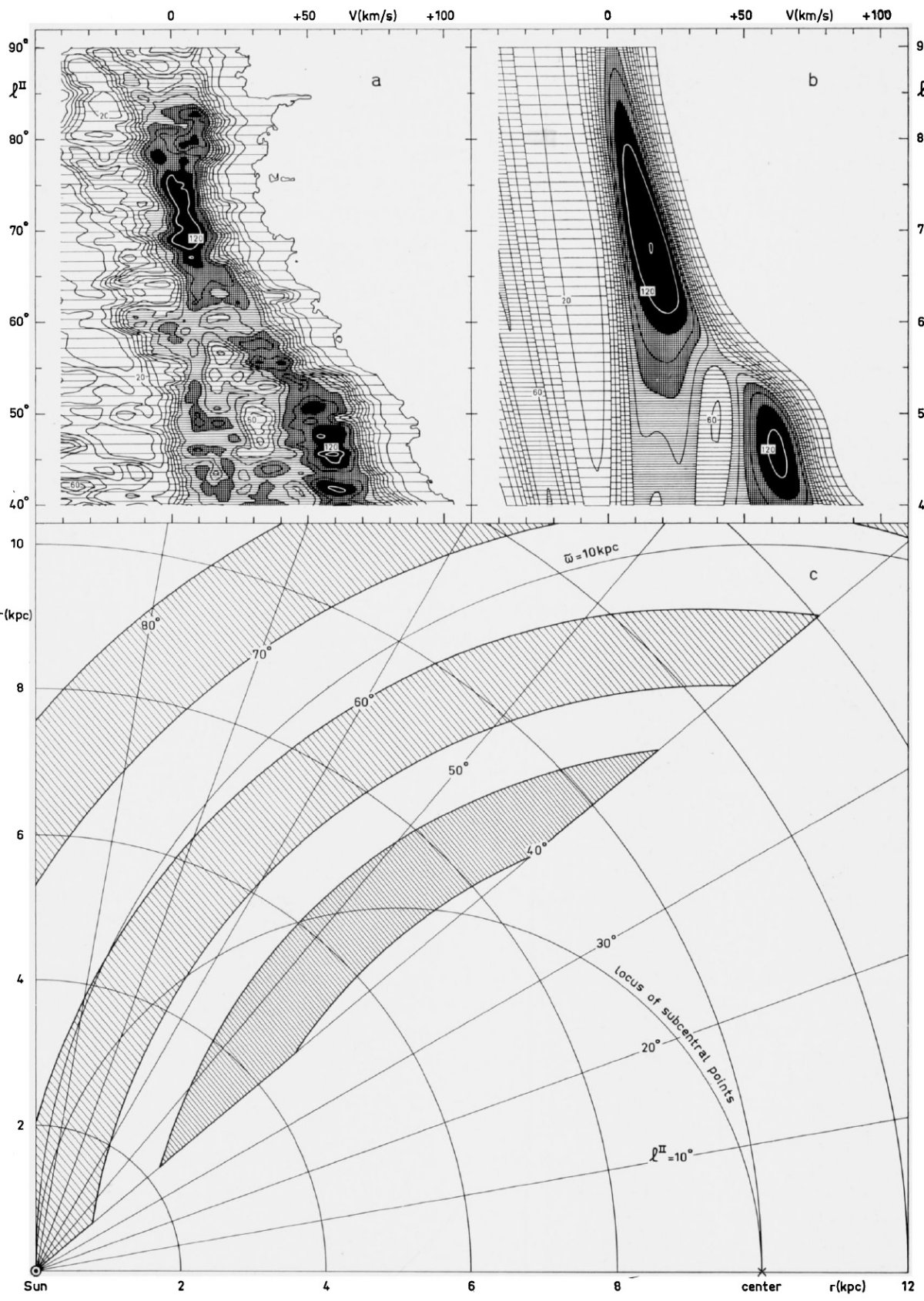
空間分布と速度場から lv 図 水素分布を導く通常の方法では、lv 図の稜線を辿り、lv 図上の点と空間 位置との間に一対一対応を仮定する。この方法を逆転させ、空間分布と速度場 から lv 図を作ると一般には観測と一致の悪い結果になることは明らかである。 (全く理解できない。なぜ観測を再現 できないのか? ) ラインプロファイルを一致させる方法 ここで提案する方法は最終空間分布から導かれる lv 図が観測と一致することに 重点を置いている。ここでは、渦状構造のマップを作る度に、ラインプロファ イルを計算する。そこには全体の幾何学効果と速度場の効果が含まれる。他の 方法でこの効果を含めることは非常に困難であろう。 その方法で解くと図13 図13にはその手法を l = [40, 90] 区間に対して図示した。図13a は 観測 lv 図、図13b は観測にベストフィットするモデル等高線、 図13c は空間分布である。図13に示すモデルは多くの点でモデル I と似る。 モデル I は一次密度波理論から予想される限り、論文 I の観測 l = [43, 56] とは良く合っているが、l がそこより大きな領域では非常に良いわけでない。 モデル V, VI は l = [65, 85] で高い放射強度を得るために、別の構造を追加 する必要はないことを示している。というのは、尤もらしい密度分布と速度場 ならどんなものでもこの区間には強い放射強度を生み出すからである。 |
太陽腕の必要性 しかしそれらのモデルでは、高強度帯が低速度で生じる。観測される速度は モデル I に含まれるような円周運動からのズレを指し示している。強調すべき なのは、問題は増強される速度であって、増強そのものではないという点である。 もし太陽付近に密度波理論型のストリーミングが存在するなら、正しい速度で 増強が起きるモデルを作ることは可能である。そのような腕が、サジタリウスと スキュータム腕を持つグランドデザインモデルにフィットしないことは真実で ある。太陽を含む腕は二次的な腕かも知れない。要求されることは、数キロパ ーセクに亘る密度波型のストリーミングである。結果として、図13では l = 90° 方向に系統的ストリーミングを持つモデルを作るために太陽付近に 腕を一本置いた。 lv図の特徴 太陽付近に腕を置くことは第2象限の v = [-15, 0] km/s 帯観測結果 のフィットを大きく改善する。こうして、図13b のモデルは、サジタリウス 腕外側の腕がピッチ角 5° を持ち、太陽銀河中心線を ω = 9.8 kpc で横切るという2点以外は、モデル I と同じである。l = [65, 85] の強度 極大は観測される速度で生じる。また密度波理論で予想されるように、l = 90 では正速度で強度極大となる。サジタリウス腕外側の腕が太陽の内側を通過 するので図13b の等高線には、遠近腕双方の効果が現れている。しかし、腕の 位置はモデルにあまり影響しないのでサジタリウス腕ほど良くは決まらない。 図13bの特長 図13b の lv 図等高線では、 Burton (1970b) の図4に示される特徴が以下のように再現されている。 (i) サジタリウス腕 A - B のループ (ii) このループの延長 AB (iii) l = 47 付近での B 最高点=接点より内側 (iv) B での dv/dl = 0 (v) l < 45 で B と D への分裂 (vi) 擬高速稜線 H (vii) E = サジタリウス外側の遠方腕 (viii) l = 50, v = 30 km/s 付近の空白域 (ix) サジタリウス腕に伴うコブ 図13b の等高線は図13c の空間密度分布から作られた。しかし、密度分布 は密度波理論を通じてストリーミング強度を定める点以外はあまり重要でない。 それでもこのモデルは lv 図の細かい点の特徴を抑えている。 |