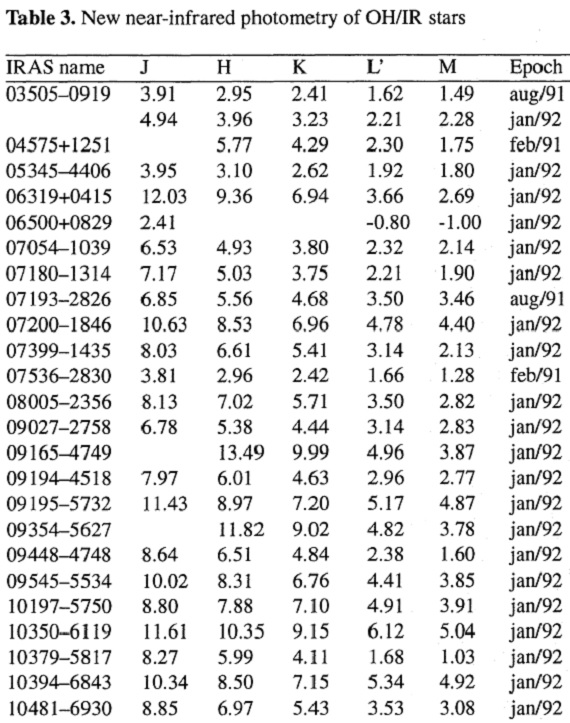
表3.新しい観測データ
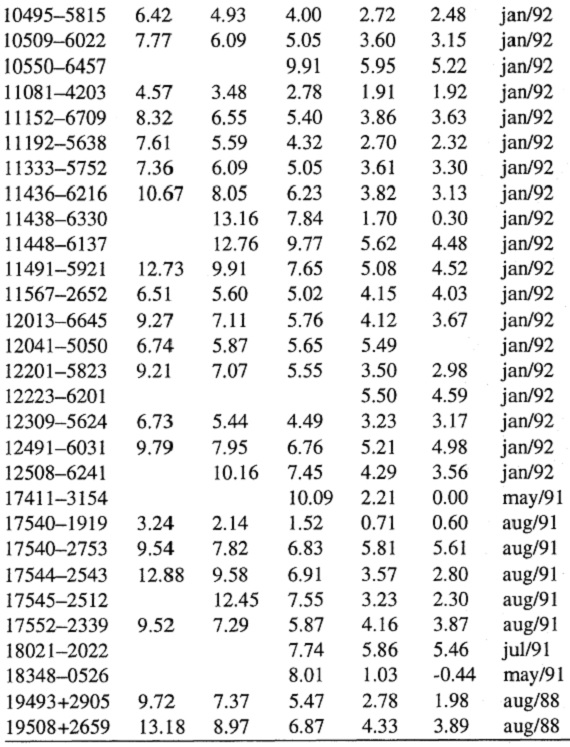
| 新しい OH/IR 星の JHKL'M 測光の結果を報告する。文献データと合わせ 約 400 の OH/IR 星に対する近赤外測光データベースを作った。AGB 星 と見做されない天体を除去した後のサンプルは、K-L' カラーの系列を得た。 星+星周シェルの簡単なモデルを作り、光度、半径、星温度、光学的深さ、 マスロス率のような基本パラメターを得た。 |
これらのパラメターは OH/IR 星の系列に沿ってスムーズに変化する。
そして、K-L' カラーがほぼ完全に OH/IR 星の物理パラメターを与えることが
分かった。メタル量は OH ピーク間隔を与える。しかし、他のパラメターには
あまり影響しない。
(OH/IR 星は一次元系列に並ぶという例の一つ?なぜ、個々の SED フィットをしてから パラメターと K-L の関係を調べないのか?) |
|
C/M 分離 C/M 分離は IRAS 二色図でも見られるが、 Epchtein, Le Bertre, Lepine (1990) が示した ように K-L 対 [12-25] 図ではもっとはっきり平行な二本のベルトとして見える。 OH/IR 星系列は進化系列か? de Jong 1983, Olnon et al 1984 は[12-25] 系列に沿って、変光周期、 光度、マスロス率、膨張速度が変化するとした。 (確かか? ) Herman (1986) はカラーだけでSED が決まると述べた。多くの研究者がこの系列は進化系列で あると考えた。しかし、それらのスケール高はカラーにより異なることが 分かった。 Ortiz, Maciel 1994 を見よ 質量系列か? Epchtein, Le Bertre, Lepine (1990) は炭素星のサンプルに対して別の説を出した。この 考えは OH/IR 星にも当てはまる。この説ではマスロス率は質量に応じて一定の 値に決まる。始まりと終了ははっきりしている。 |
どちら? 二つのどちらが正しいのだろうか?それとも進化段階と質量は共に重要なの だろうか? PN との関係 Ortiz, Maciel 1994 は、 彼らのクラスI OH/IR 星は Peimbert のタイプ I PN と空間密度、 運動、質量の点で類似していると指摘した。親子関係なのかも知れない。 K-L との関係 このように、OH/IR 星の正確な性質を知ることは重要である。ここでは 400 OH/IR 星について、 NIR, IRAS データを解析する。特にそれらを K-L カラーとの関係で調べる。 |
|
第1段=OH/IR 星統合カタログの作成 研究のスタートは、既存カタログを合わせて、約 1500 OH/IR 星の最新カタ ログを用意することである。使用したカタログの出所は Ortiz, Maciel 1994 の表1にある。その主要部は te Lintel Hekkert 1989 であるが、それ自身が 過去のカタログを集めたものである。入力天体は IRAS 名で名付けられた。HIIR, または非恒星天体などを省いた。 |
第2段=NIR天体の同定 主に 1992 年 ESO 1 m 望遠鏡による撮像を利用して、近赤外天体との同定 を増やした。表1にその参考文献も載せた。それらは、既知 OH/IR 星の約 30 % に上る。 (VizieR によると表1は 405 天体の IRAS 名と参考文献、表2の方に それらの OH 情報と J,H,K が載っている。) |
 表3.新しい観測データ |
 |
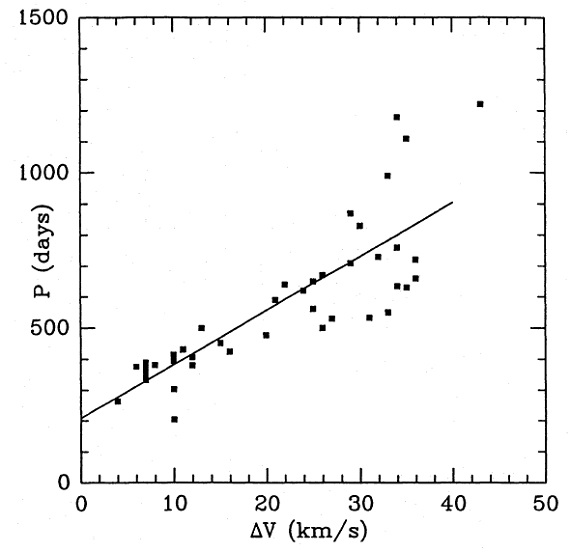 図1.OH/IR 星の周期-ΔV 関係 104Lo 法 通常用いられる簡便法では L = 104Lo を仮定する。しかし、 周期光度関係からの見積もりでは OH/IR 星の光度幅は大きい。 方法1=光度法 Ortiz, Maciel 1994 は Feast 1989 の周期光度関係を使用して、周期から輻射等級を推定した。不幸なことに、周期 が知られている OH/IR 星の数は少ない。 その場合には Dickinson et al 1975 の周期-ΔV 関係を用いた。ただし、 Engels et al 1981, Whitelock et al 1991 のデータを追加して、図1では 47 星をプロットした。この標準偏差は 123 日で輻射等級では 0.4 等に相当 する。 見かけ輻射等級 見かけ等級は星間減光の補正を行い、 Koornneef 83 のゼロ点フラックスで フラックスに変換した。 (減光補正の内容の記述はない。) 総フラックスは IRAS と NIR データで行った。 λ > 60 μm 部分の 補正は Ortiz, Maciel 1994 に倣った。 |
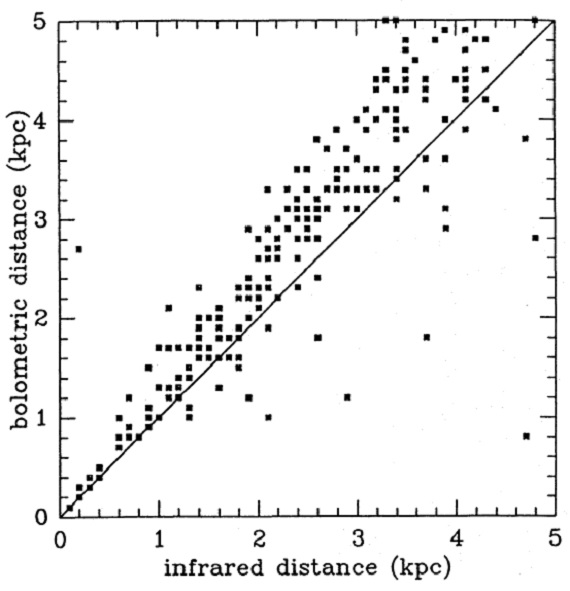 図2.方法1=輻射等級法と方法2=F25, L 法から決めた距離の比較。 方法2= K-L 法 第2法は K-L と絶対等級 M25, ML との間の緊密な 関係に準拠している。これは、Whitelock et al 1991 が K-L > 1 のバルジ LPV に見出した M25 - (K-L) 関係と Whitelock 1990 による ML - (K-L) 関係を使う。変光、SED の勾配を考えると、K-L > 1 では M25, K-L ≤ 1 では ML が適当である。 (Ita, Matsunaga 2008 の P-M(L) 図は3等の L 巾を示す。タイトな (K-L)-logP 関係が存在しないとこの話は 怪しいが。 ) 減光補正 減光補正には Ortiz, Lepine 1993 の減光モデルを使用した。このモデルは ダスト分布がガス分布(HI + H2)に比例するという仮定に基づい ている。この方法は Bloemen et al 1990 が 100 μm 輝度分布を再現する際に 用いた方法と類似している。単位距離当たりの減光は銀河中心方向に進むにつれ 増加していき、r = 3 kpc 付近で極大に達し、1.2 kpc で極小を持つ。これはまた、 de Jong 1983 のモデルともあまり変わらない。個々星に対する減光補正値と距 離は逐次近似して定める。 図2=二つの方法の比較 図2に示すように二つの方法で決めた距離はよく一致する。 |
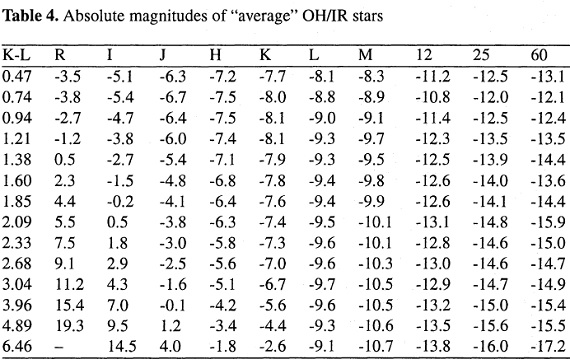 表4.「平均」OH/IR 星の絶対等級 「平均」OH/IR 星 K-L' の狭い範囲に属する OH/IR 星は共通の SED を有すると考える。 平均をとることで、赤化補正の誤差や、変光の影響を減らせる。そこで、 K-L' を14区分に分けた。各区分には 10 星以上が入る。それには 次の星が含まれない。 (1)全バンドでの等級が決まっていない。 (2)輝線間隔が 40 km/s 以上(超巨星) (3)|z| < 50 pc (減光大) (4)二つの方法で決めた距離がファクター2以上の違い。 表4にこうして決めた「平均」OH/IR 星の絶対等級を示す。 |
 図3.「平均」OH/IR 星の絶対等級 図3=(K-L)-M 関係 図3には表4の結果を図示した。等級の標準偏差は 0.3 mag である。ただし、 K-L 小のサンプルに対する M(60), K-L 大のサンプルに対する M(J)の ような場合には誤差は 2 mag に達する。表5に近似式係数を示す。 |
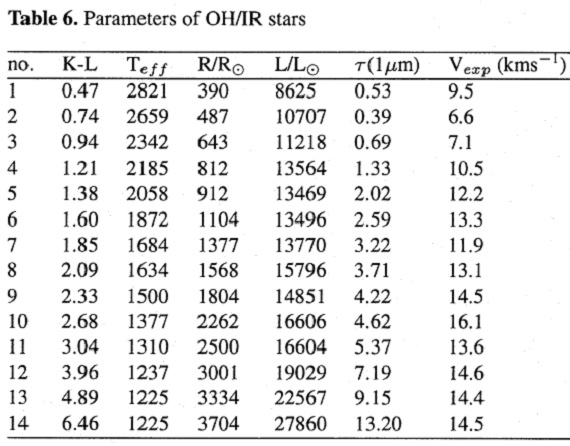 表6.表4の平均 OH/IR 星のパラメター 密度、温度構造 中心星は半径 rs, 温度 Ts の黒体。ダストシェルは r = [rint, rext] で ρ ∝ r-2 を仮定する。さらに、log (rext/rint) = 2.5 とする。 r = rint でダスト温度 Te とする。 温度分布は Rowan-Robinson, Harris 1983 や Le Bertre 1987 の輻射輸達モデルに倣い、 T ∝ r-0.4 を仮定する。 τ ダストシェルの光学的深さは、Mathis 1990 の星間減光曲線に倣い、 メイン部を τ(main,λ) = τ(1μm)λ-p と仮定する。 ここに、p=1.7 (λ<9μm), p=1.1 (λ>9μm) である。 シリケイト帯は、τ(silicate,peak) = 2.5 τ(main,peak) を peak = 9.8, 19 μm で τ(main,peak) に加える。9.8 μm 帯は 半巾 2 μ, 19 μm 帯は 半巾 4 μ のガウシャンとする。 ダストシェル内端温度 Te 輻射平衡を仮定すると、ダストシェル内端の温度 Te と半径 rint には次の関係がある。 |
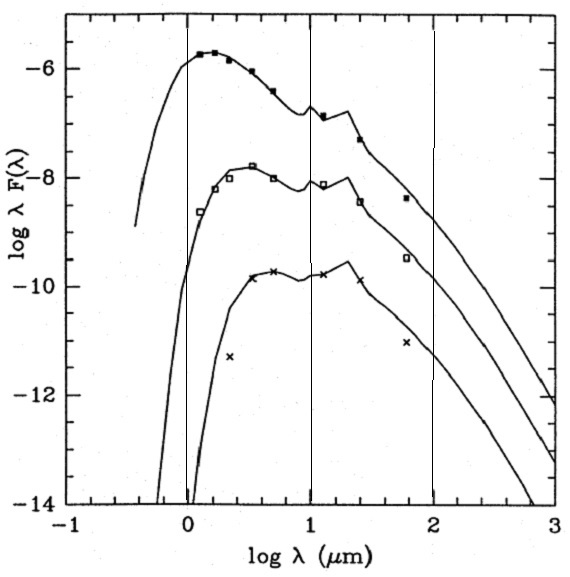 図4.表6の平均 H/IR 星 no. 1, 7, 13 の SED とモデルフィット. rint = (rs/2)(Ts/Te)(p+4)/2 p = 1.1 の方を採用する。ベストフィットは単一温度 Te = 250 K で得られた。 フィッティングパラメター rext/rint は結果にあまり影響しない。上に述べた通り、 Te は固定された。そこで、残るフィッティングパラメターは Ts, Rs, τ(1μm) となる。 ダストシェルのSED 密度、温度分布、オパシティ分布が決まったので、光路に沿って放射と吸収 が積分していける。全光路を集めてシェル SED が求められる。 |
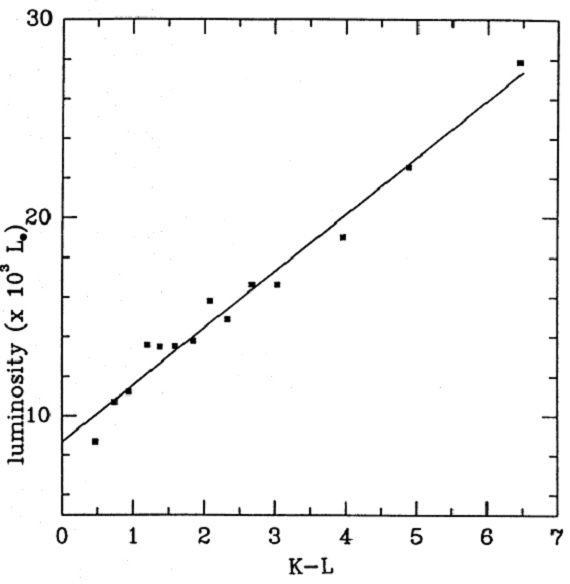 図5.L(平均OH/IR星) - (K-L) 関係。フィットは, L/103Lo = 8.67 + 2.87 (K-L) |
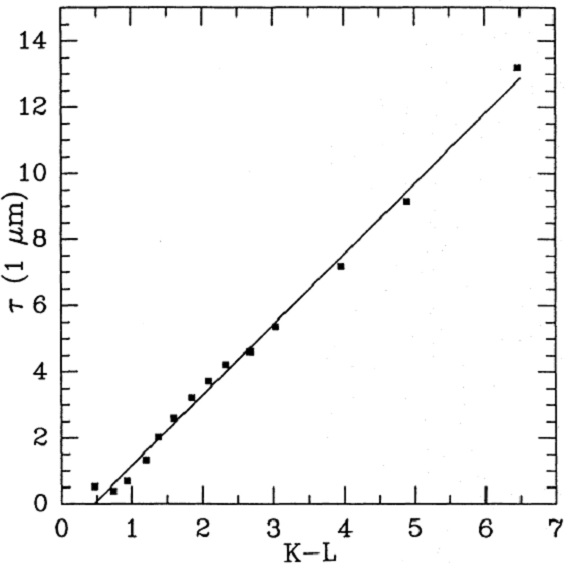 図6.平均 OH/IR 星の τ(1μm) - (K-L) 関係。フィットは τ(1μm) = -0.97 + 2.13 (K-L) |
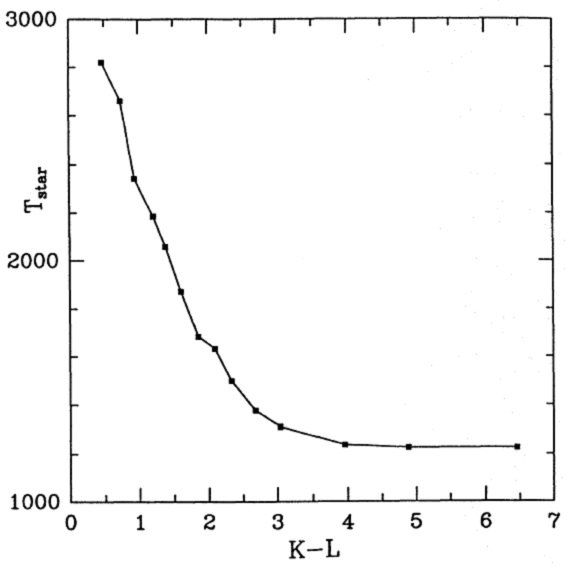 図7.平均 OH/IR 星の Ts - (K-L) 関係 表6=平均 OH/IR 星の性質 表6に平均 OH/IR 星の性質を示す。Ts(Teffと書かれている), Rs/Ro, L/Lo, τ(1μm), がフィッティングで決めた値である。Vexp はスペクトル線間隔/2 の平均値である。 図4=平均 OH/IR 星の SED 図4には平均 OH/IR 星の SED を示す。表4には SED 外挿で決めた M(R), M(I) を 載せた。この二つは銀河系の星計数モデルでは重要である。 シリケイト帯は直接には扱わなかった。というのは、我々のデータがバンドを 直接扱っておらず、また吸収帯の中には星間吸収起源のものが多く含まれている からである。 (なるほど、しかしそれなら連続光の SED も星間減光の影響を強く受けた ものが多いことにならないか?) まあ、しかしとにかくグループ14には吸収帯が現れている。 フィットで得た主な結果 フィットから得た主な結果をまとめると、 (1)L(OH/IR) = [8, 30] 103 Lo の範囲を占め、図5に見るように、 星間赤化補正した K-L と線形な関係にある。 (log L でなく、L なのに注意。しかし、Mbol でも同様の結果が 得られそう。) (2)τ(1μm) も (K-L) と線形関係にあることが図6から分かる。 (3)図7は星温度 Ts が 1200 K まで下がることを示す。それに伴い、星 半径 Rs は図8に示すように 4000 Ro まで広がる。 |
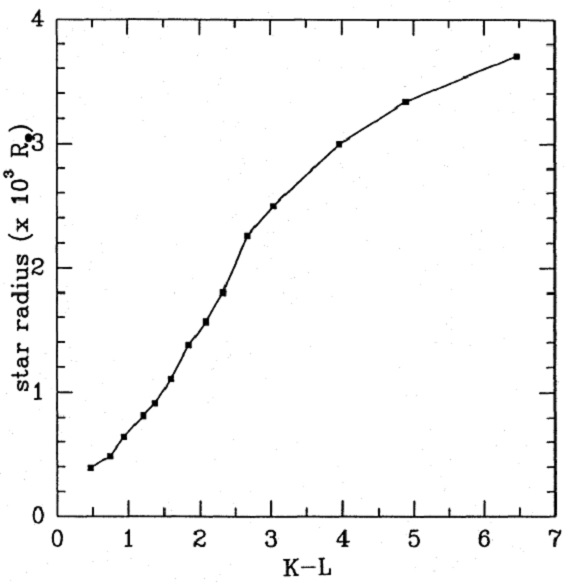 図8.平均 OH/IR 星の Rs - (K-L) 関係 ここで求まったパラメターは CSE の細かい点には影響されない。 オパシティを λ-2 としても、密度を厳密に r-2 としても結果はそう変わらない。Ts, Rs で 10 %, L, τ で 20 % 程度の変化である。 星質量の範囲 平均 OH/IR 星 no.1 と 2 は、光度、温度、半径に関して、 Bessell et al. 1989 1 Mo 星モデルグリッドの最晩期星に対応している。別のメタル量モデル も同様の結果である。観測された周期はファクター 10 の範囲、表6から、 半径もファクター10、周期 P ∝ ρs-1/2 から、質量範囲は [8,10] Mo のファクター10程度になる。しかし、この議論 は初期質量に基づいている。マスロスの結果、周期は時間と共に増加する だろうから、周期巾のいくらかはこの効果でも説明できる。 星温度とダストシェル内端温度 OH/IR 系列最晩期の Ts = 1200 K は驚きの値に見えるかも知れない。この 温度範囲のモデルは存在せず、強い分子バンドが効き、黒体近似は不正確と なり、 Ts の不定性は大きい。 もう一つの驚きは、ダストシェル内端温度 Te = 250 K である。多分、800 K 付近で形成されるシリケイトでは 9.7 μm 以外では力不足で、氷が大きな 役割を受け持っているのではないか?興味深いことに、Te の違いが OH/IR 星 と炭素星との大きな違いの原因となっている。炭素星系列からの SED は Te 1000 K でうまく説明 (Epchtein, le Bertre, Lepine 1990) できる。 (しかし、それって、OH/IR 星全てで H2O 3 μm 帯が見えることになるけど。 ) この Te の差が (Epchtein, le Bertre, Lepine 1990) が述べている [12-25] - [K-L] 図上で O-リッチと C-リッチとの差を説明する のだろう。光度と光学的深さが K-L で決まることは大変有用である。 (赤化補正が正確にできるという条件 付きだが。) |
|
マスロス1 Netzer, litzer 1993, Gail, Sedlmayr 1987 は τ, dM/dt, Vexp の関係 を導いた。ここでは簡単に復習する。r = rint で V(rint) = 0 と仮定し、加速はもっぱら放射吸収によると仮定する。ラグランジュで考えて、 ( dV/dt = κFo exp(-τ) (κ=単位マス当たりの吸収係数) τ=∫κρdr ウーン、この先へ行かない ) 速度則は、 v(r) = U[1-exp(-τ(r))] ここに、τ(r) は rint と r の間の光学的深さである。 τ(r) の近似表現は、 τ(r) = τ(r)max(1-rint/r)1/2 (これは逆二乗則の場合の式 じゃないな。なんだろ?) 密度 ρ(r) は dτ = ρ(r)χdr なので、上式を微分して得られる。 この近似で得られるマスロス率はより単純な r-2 則からのマスロス率 に比べ、ファクタ2異なる。 (Epchtein, le Bertre, Lepine 1990) を見よ。 dM/dt = 2πrintτ(1μm)vterm/χ(1μm) (5) マスロス2 次のマスロス式は、最終運動量を吸収光の運動量に等値したもので、 dM/dt = Lτ/cvterm ここで、輻射から移る運動量が L(1-e-τ)/c でなく Lτ/c で あることに注意。二つは τ 小では一致し、τ 大では多重散乱の効果で シェルが得る運動量は光の運動量より大きくなる。τ は有効波長における 光学的深さだが、その評価は難しい。我々は補正項 β = τ/τ(1μm) = λeff1.1 とした。λeff は 星を黒体近似したときのピーク波長(ウィーンぼ法則)である。これから、 vterm = (Lχ(1μm)β/2πcrint) 1/2 (7) を得る。星間減光を dAv/dx = 1.1 mag/kpc とし、ρ = 0.5 H cm-3 とすると、χ(1μm) = 160 g-1cm2 である。 |
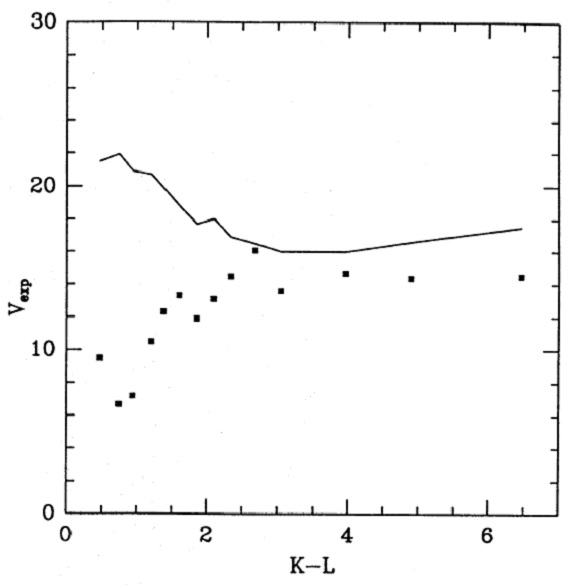 図9.OH/IR 星の vexp - (K-L) 関係。実線=式7で計算した vterm. vterm の正しさ 図9に示す vterm は観測速度と上の表式の驚くべき一致を示し ている。τ が小さい時に OH ピーク間隔が表式より小さいのは、そのような ミラ型星では OH 励起が星表面近くに移るためである。実際、ミラ型星で星風の 加速が観測されている(Lepine 1987) ( CO と OH で差? ) |
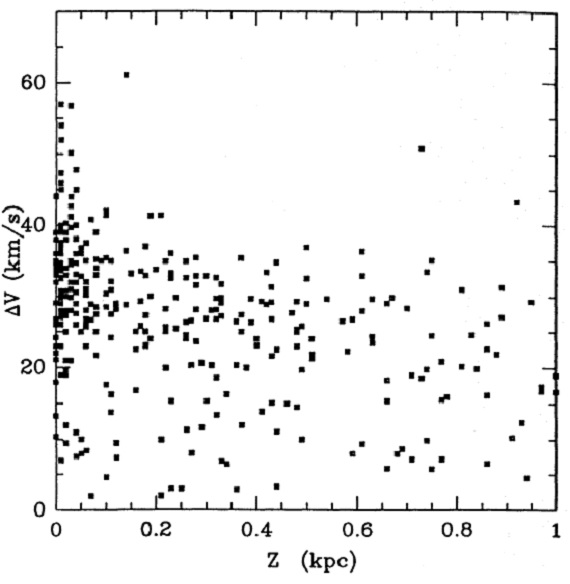 図10.OH ピーク速度と銀河面高度 z との関係 図10: OH 線間隔 ΔV と銀河面高度 z の関係 図10には OH 線間隔 ΔV と銀河面高度 z の関係を示す。 z が上が ると ΔV が減少する傾向が見られる。これは式 (7) に見られる通り、 χ がメタル量に比例する効果と考えられる。 図11=マスロス率と (K-L) の関係 式(5) に式(7) を代入して、マスロス率を計算した。図11には我々の平均 OH/IR 星に対して計算したマスロス率をプロットした。 マスロス率は 5 10-6 Mo/yr - 7 10-4 Mo/yr の範囲 に広がる。最終質量を白色矮星に合わせるためには、ミラ型期の長さは 1 Mo で 2 104 年、 8 Mo で 104 年と見積もられる。 図12=マスロス率の分布 図12には Ortiz, Maciel 1994 のクラス I, II, III OH/IR 星のそれぞれに対するマスロス率のヒストグラムを 示した。このクラスは Peimbert の PN タイプ I, II, III の前駆天体と見做 される。 ( 平均 OH/IR モデルでなく、個々星 のマスロスをどう出したのか? ) この図は PN 分類がぼ天体質量に対応するという考えを支持する。 ( ここの理屈は? ) |
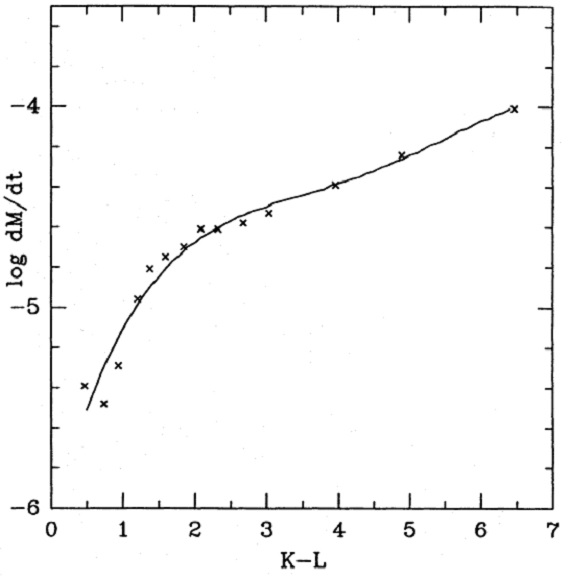 図11.マスロス率と (K-L) との関係。4次式でフィットした。 (K-L) は平均 OH/IR 星の指定に用いているだけ。 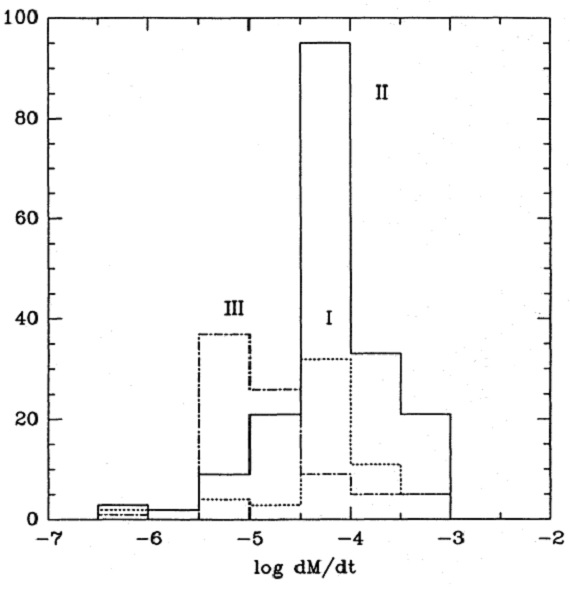 図12.マスロス率ヒストグラム。OH/IR 星のクラス分けは Ortiz, Maciel 1994 のもの。 |
|
ミラ-OH/IR 系列 NIR と IRAS データの解析から、可視ミラ型星から赤外 OH/IR 星への1次元 系列を見出した。この系列を K-L カラーで指定した。注意すべきはこの系列 から外れる、 VY CMa, PZ Cas のような超巨星、OH231.8+4.2 のような PPN が 存在することである。 進化モデルとの比較 我々の結論は大体は Vassiliadis, Wood 1993 の結論と、特に高質量星の側で、合っている。マスロス率は主に光度で規定さ れ、それはマスロス期間中あまり変わらないコアマスで定まる。 ただし我々の得たマスロス率は大きめで、期間は短く、星温度は低い。 |
小質量星のマスロス停止現象 小質量星に対し、 Vassiliadis, Wood 1993 はマスロスはその停止期間を挟んだいくつかの活動期に分かれることを示唆し ている。このマスロス停止に関しては観測的な証拠 Zilstra et al. 1992 も存在する。そのような現象に関し、我々のモデルは十分な近似になっていない。 それが青い K-L 星に対する散らばりの大きさを説明するのかも知れない。 マスロス加速はない SED はマスロス一定でフィットできた。我々は、ミラ-OH/IR 系列は 主に初期質量の系列である。 Ortiz, Maciel 1994 が述べたように、OH/IR 星は Peimbert 1978 が提案した PN の性質がぼ天体質量で決まるという話の OH/IR 版である。 |