The Milky Way Tomograohy with SDSS I. Stellar Number Density Distribution

　アブストラクト

　１．イントロダクション　

　２．データとその処理方法　

　２．１．ＳＤＳＳ　の特性　

　２．２．測光視差法　

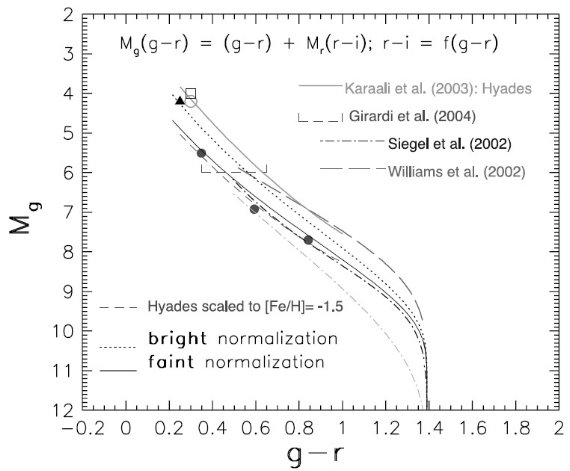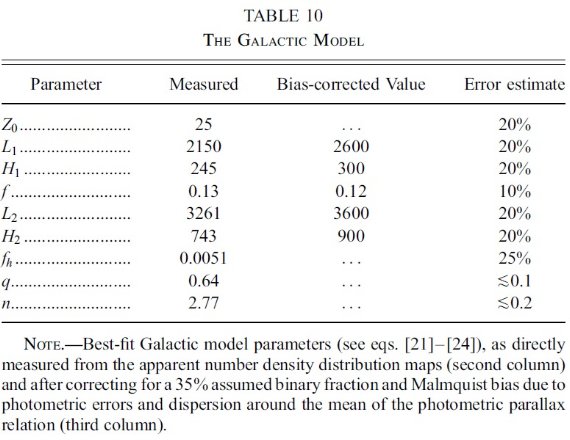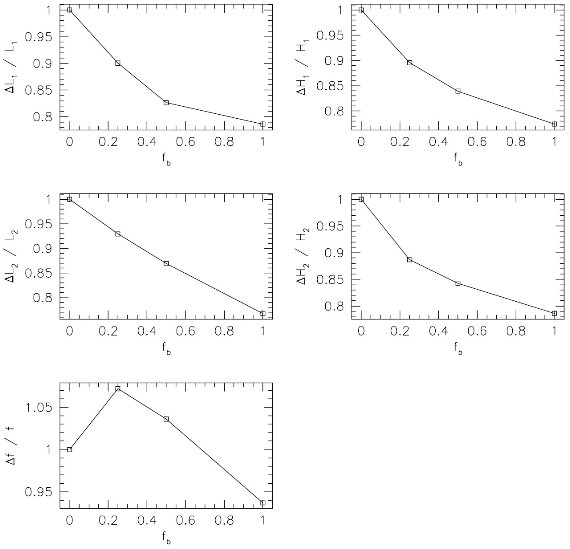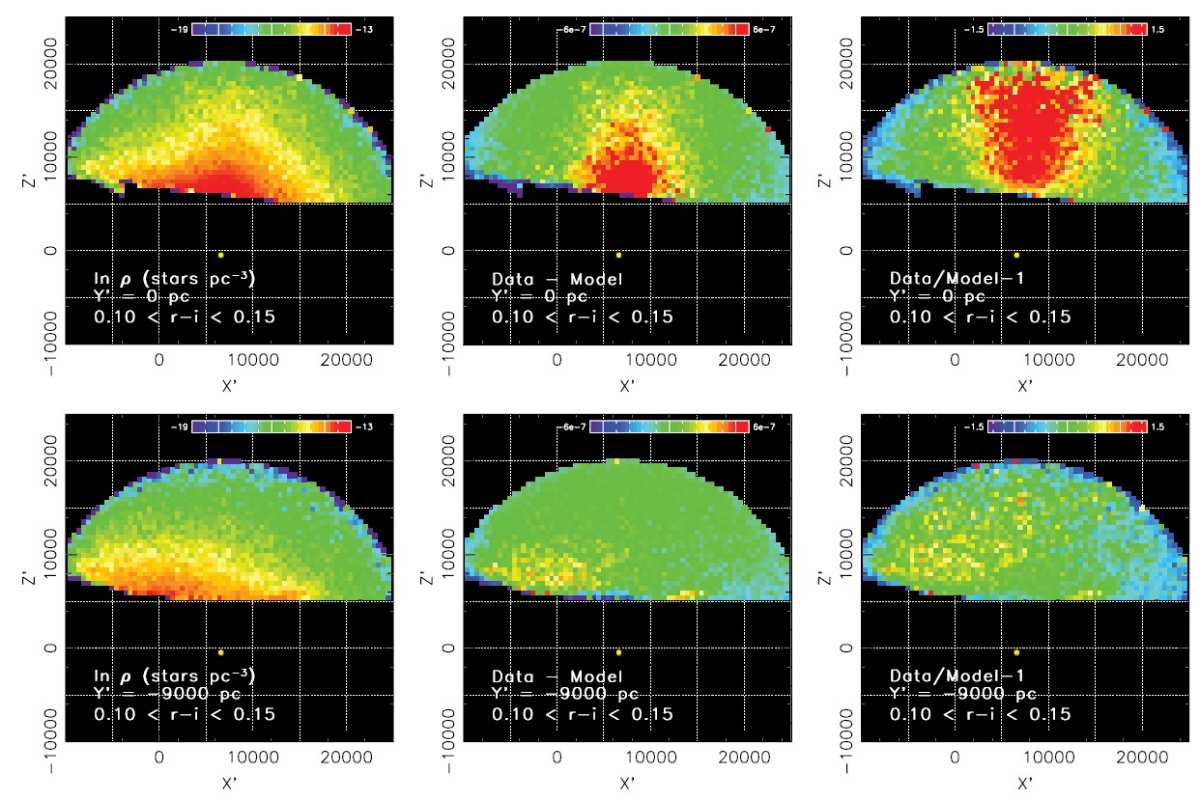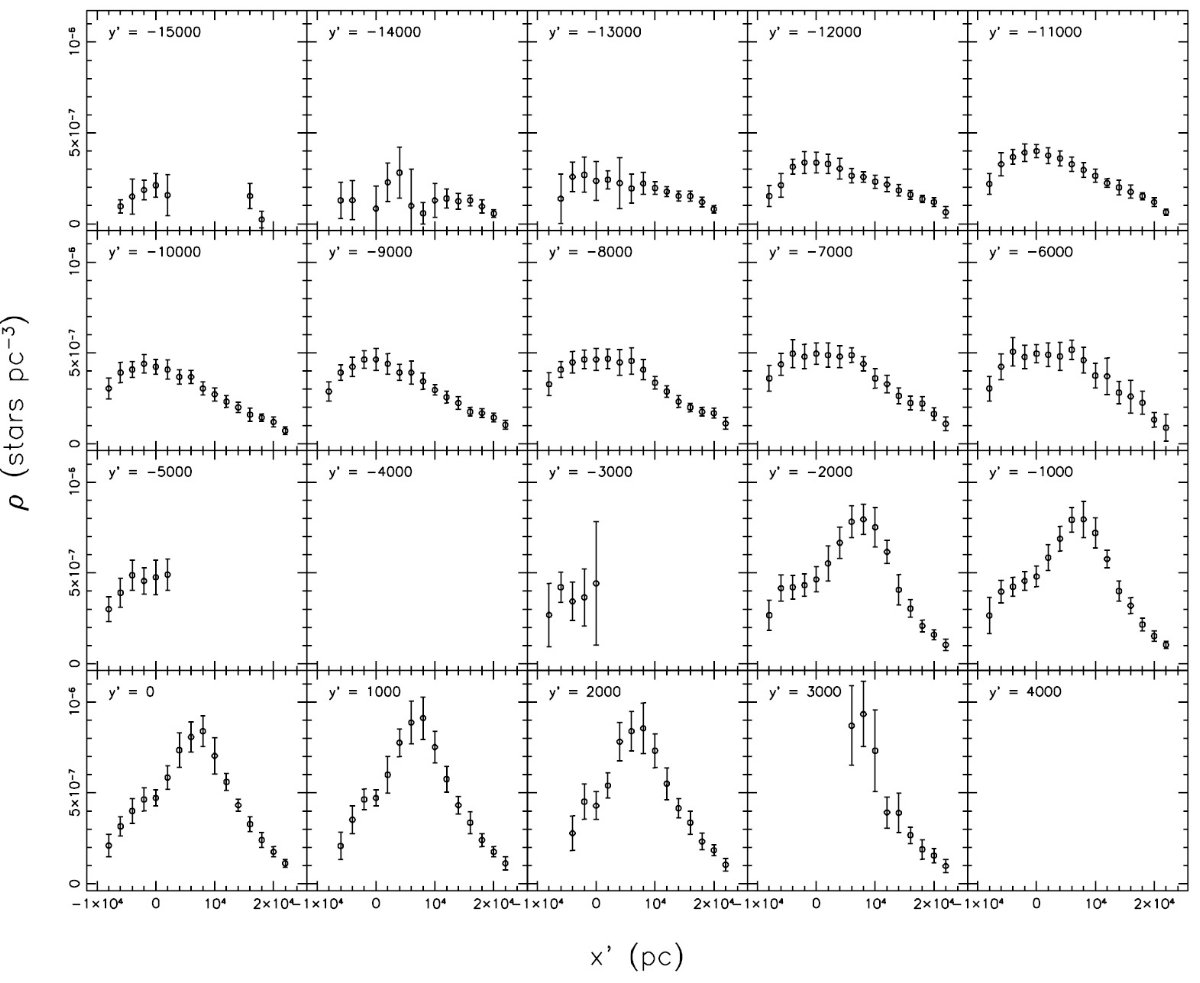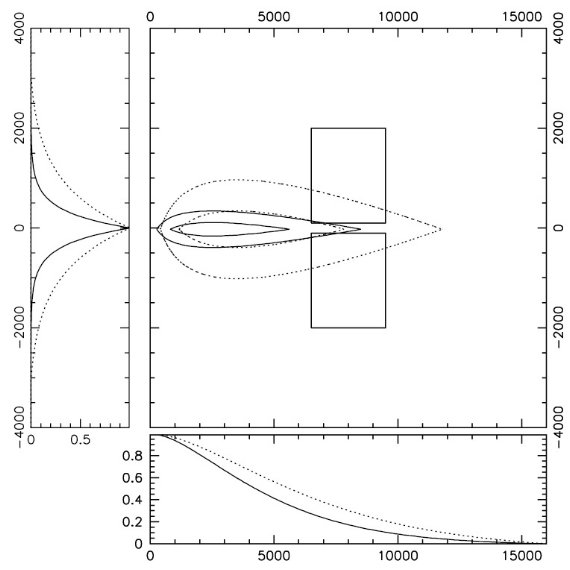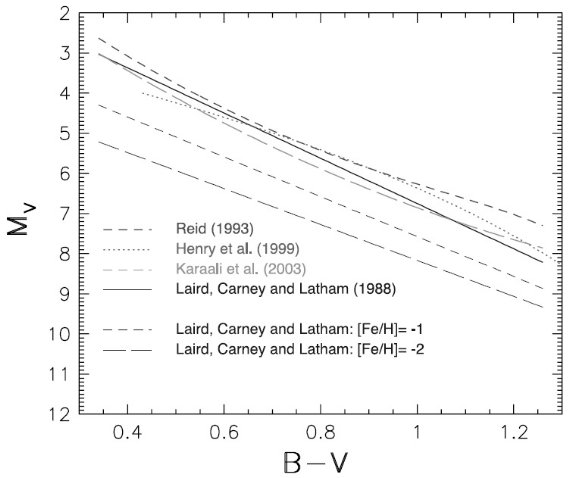
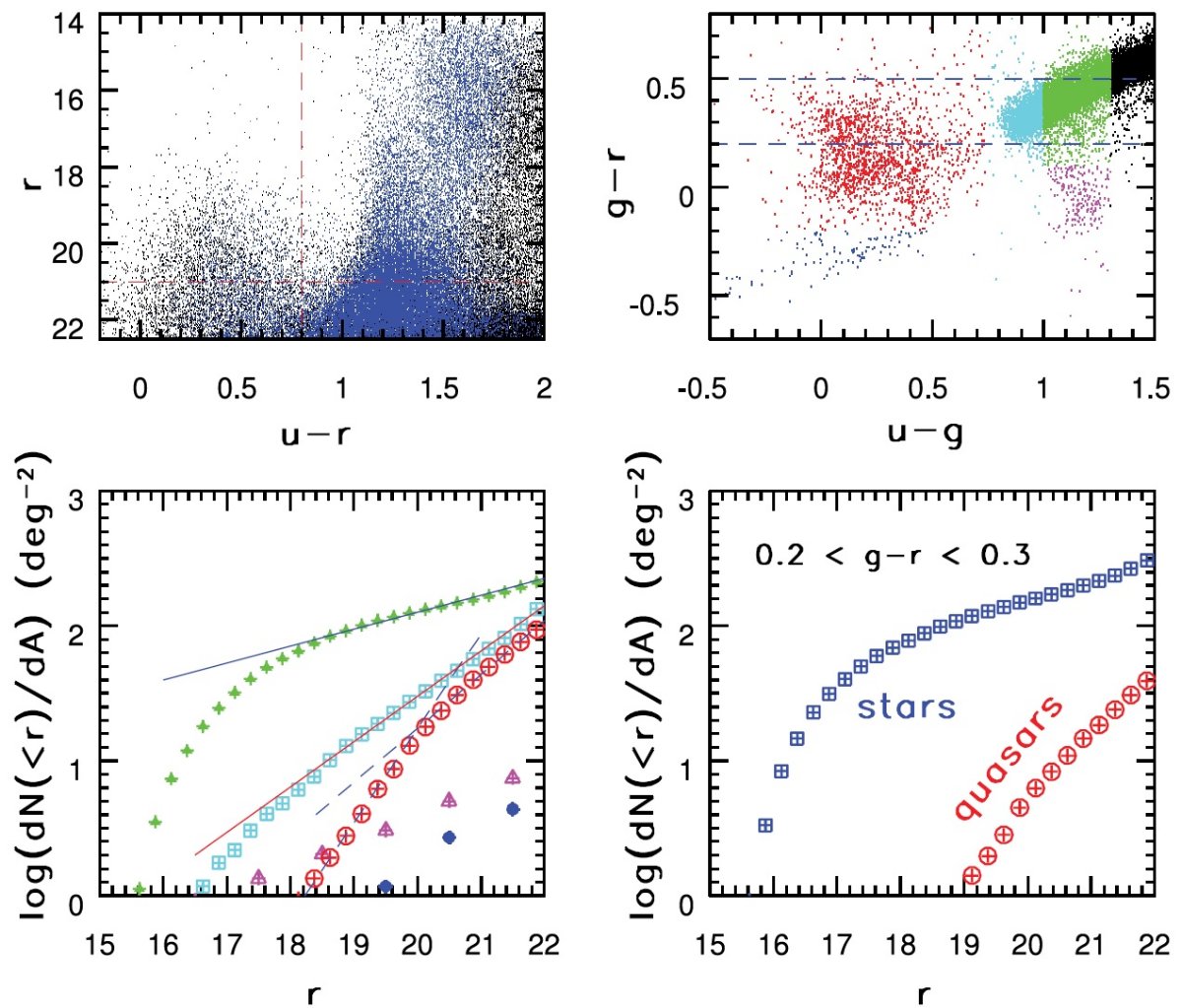
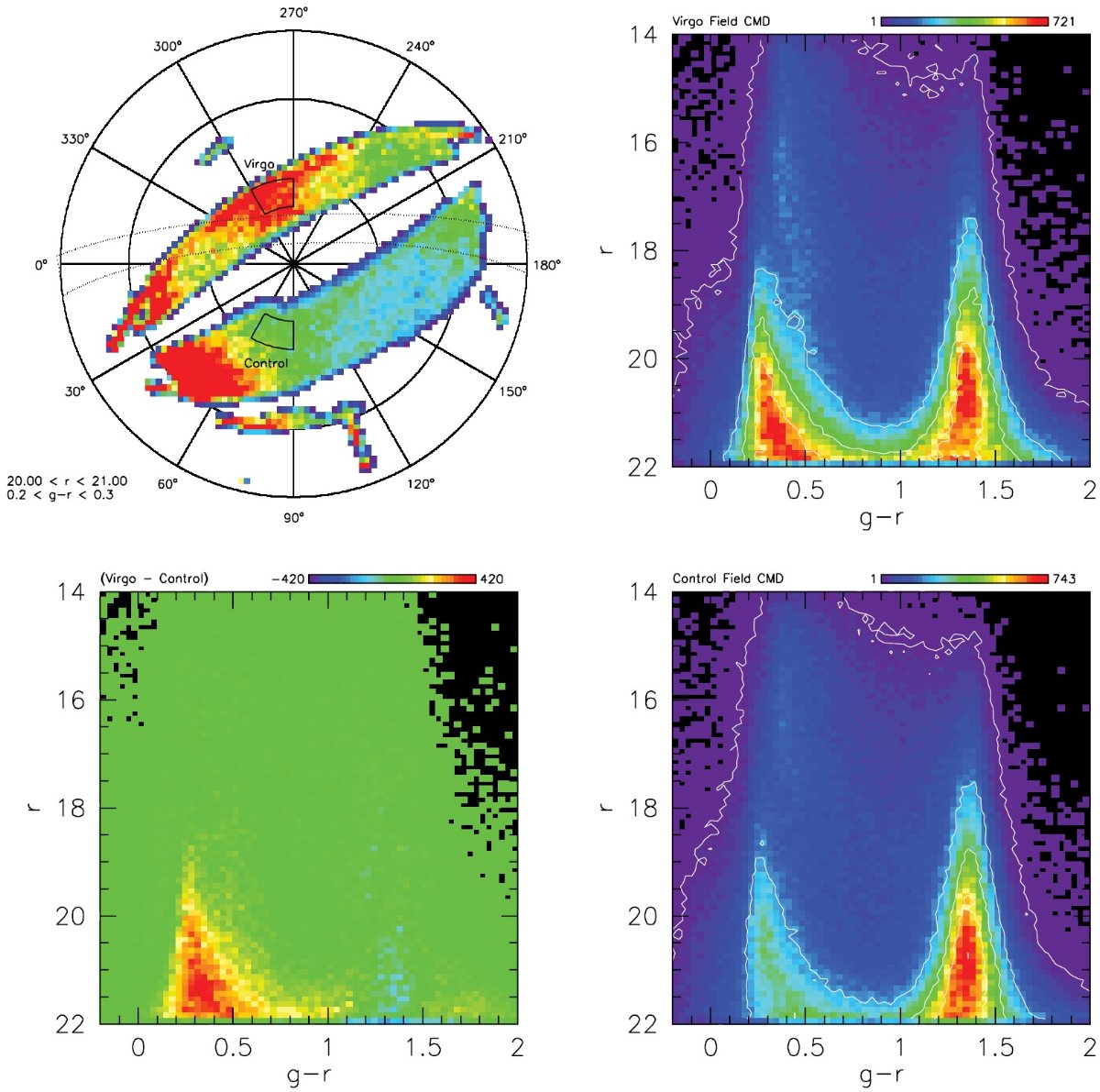
図１．測光視差関係の比較。 Henry et al 1999 は D < 10 pc の星から。 他の関係はヒアデス MS を用いている。後者は十分の数等違っていることに注意。 Laird et al 1988 は二つのメタル量に対して示した。dMv/d[Fe/H] = 1 mag dex -1 である。 SDSS の 98 % は主系列星　 　SDSS が検出した星の 98 % は主系列星である。そのカラー等級関係はかなり よく決まっている。多くの関係が、視差の分かっている星、星団の星などを使って 求められてきたが、図１から分かるように十分の数等の誤差がある。

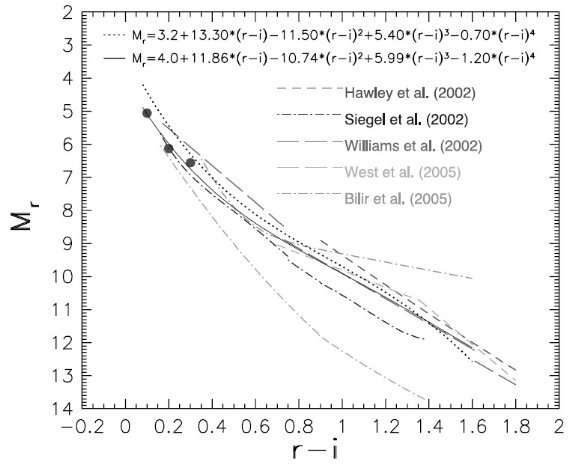
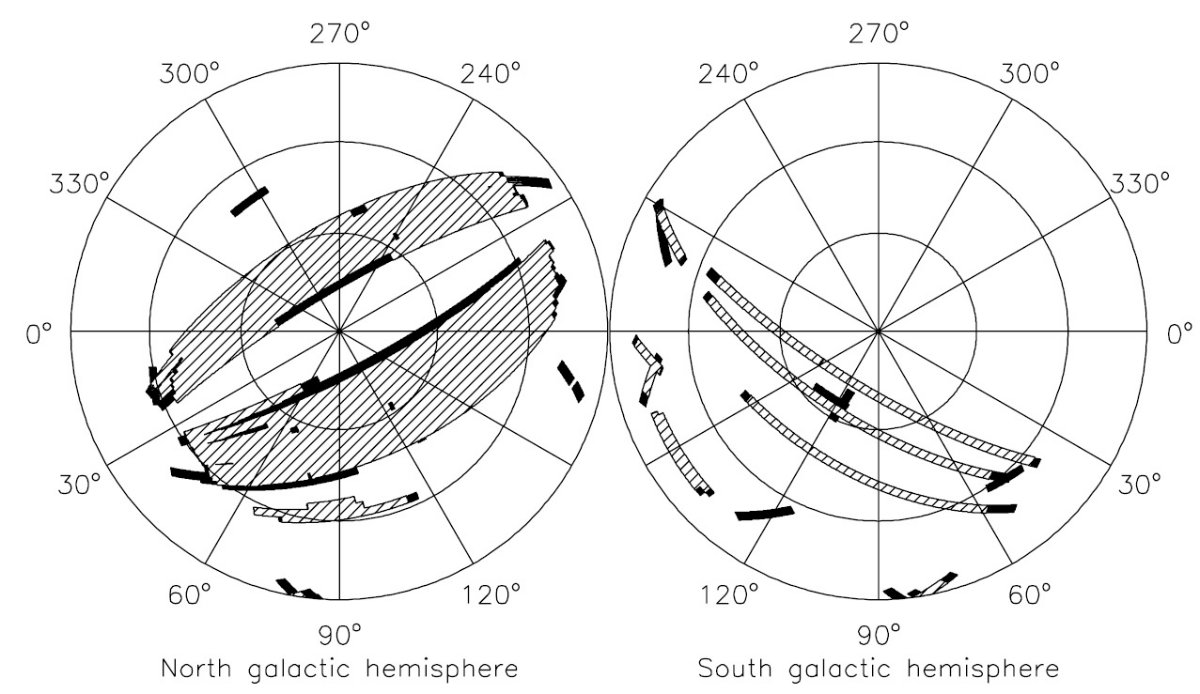
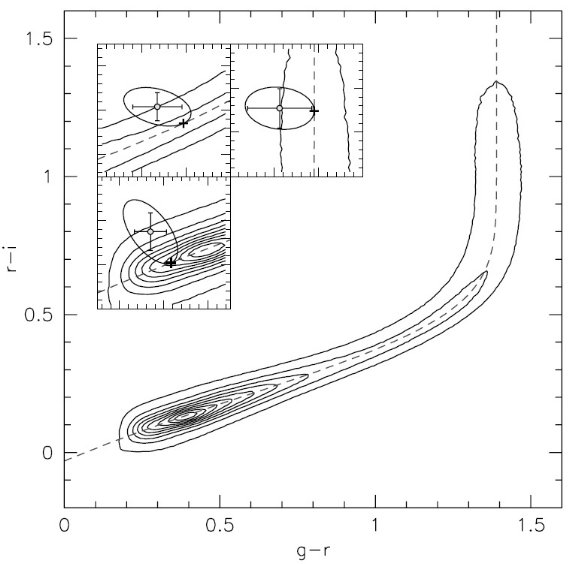
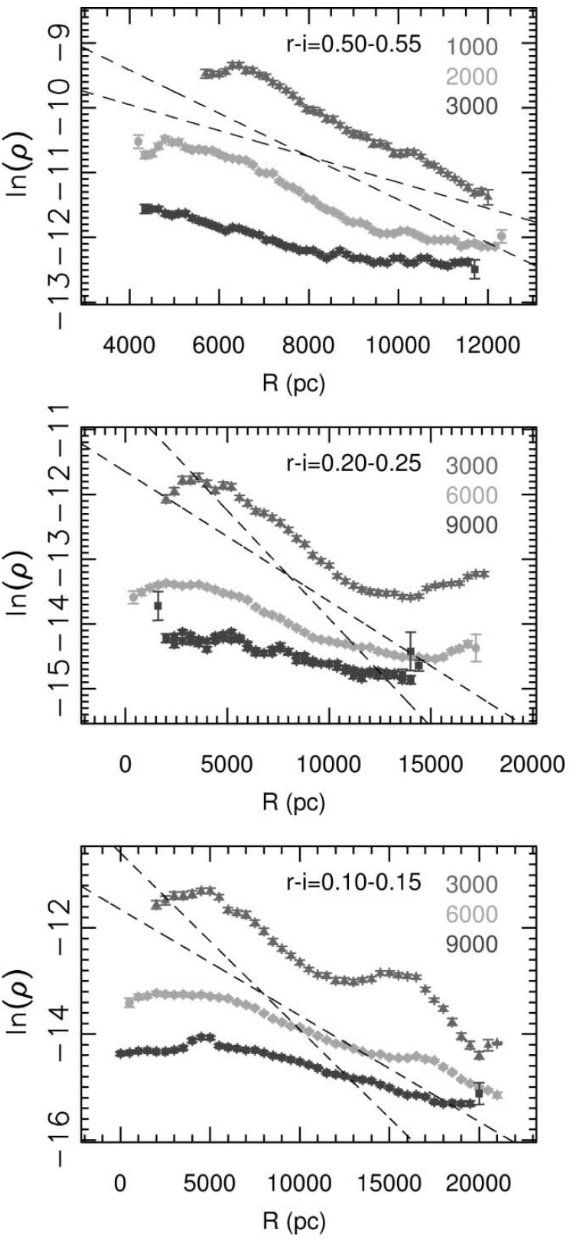
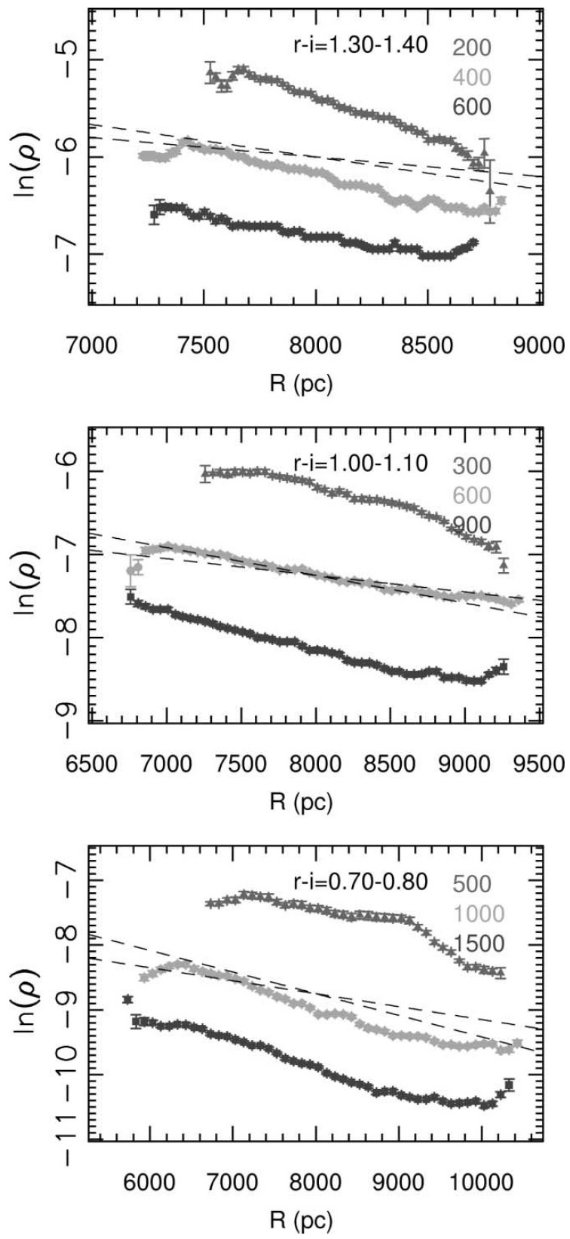
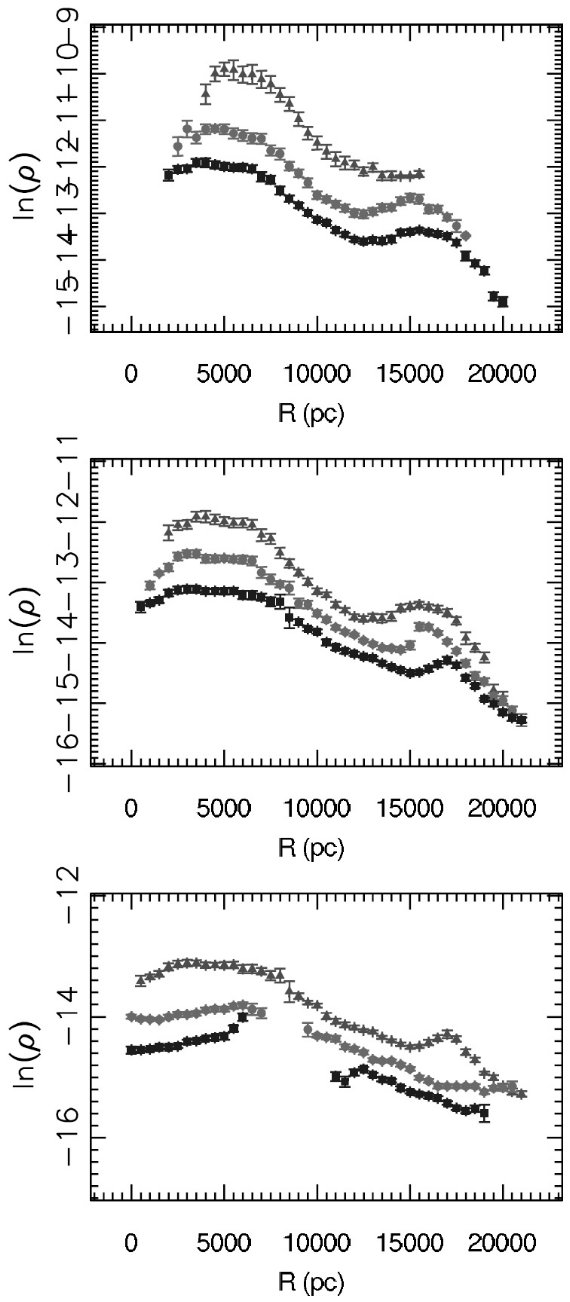
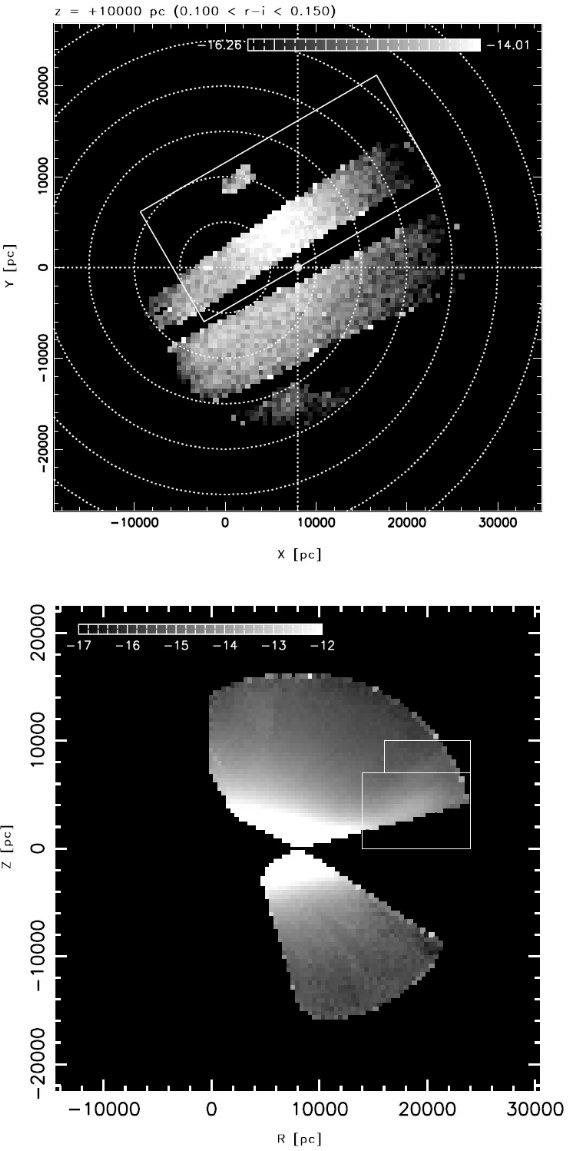
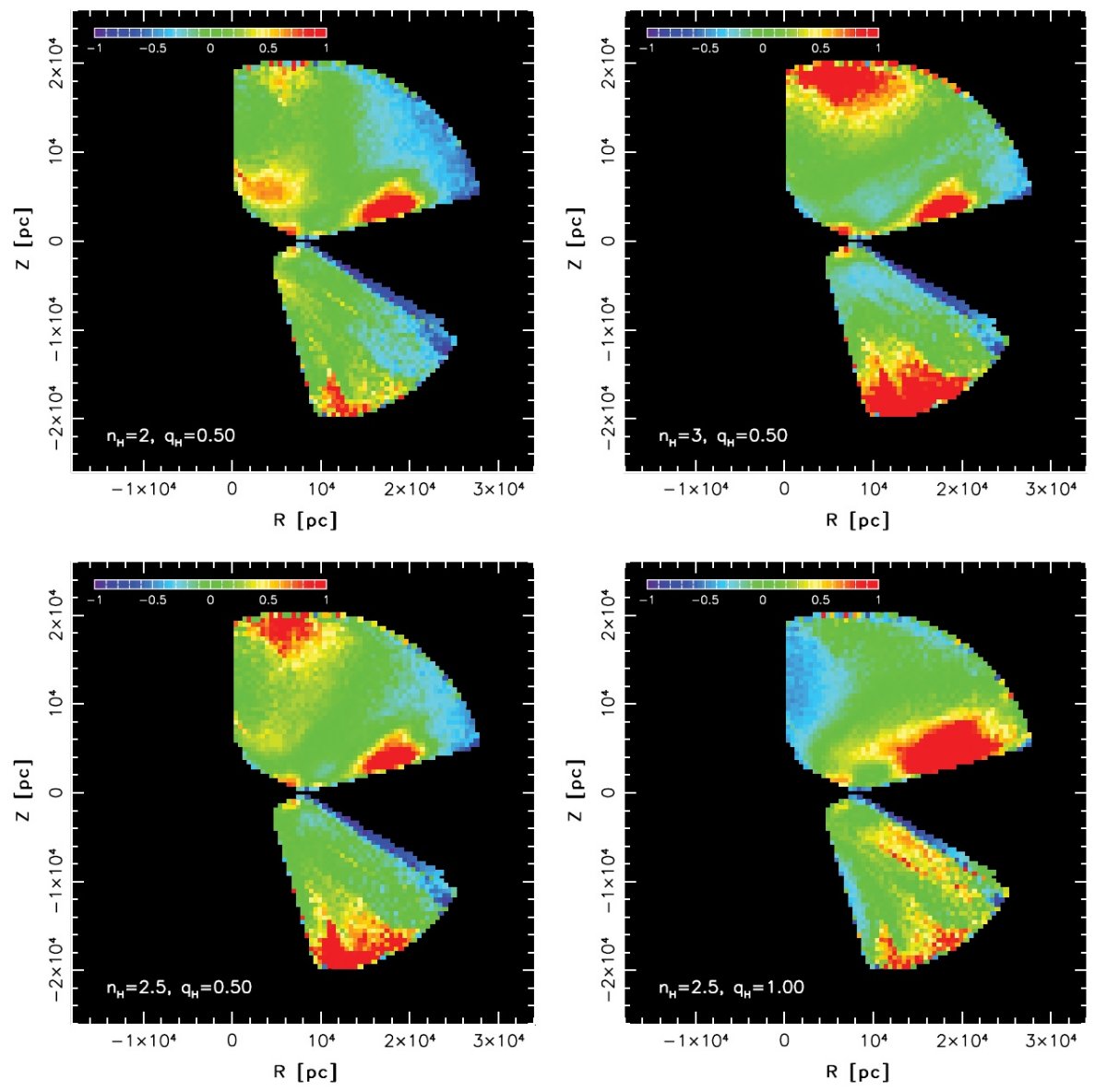
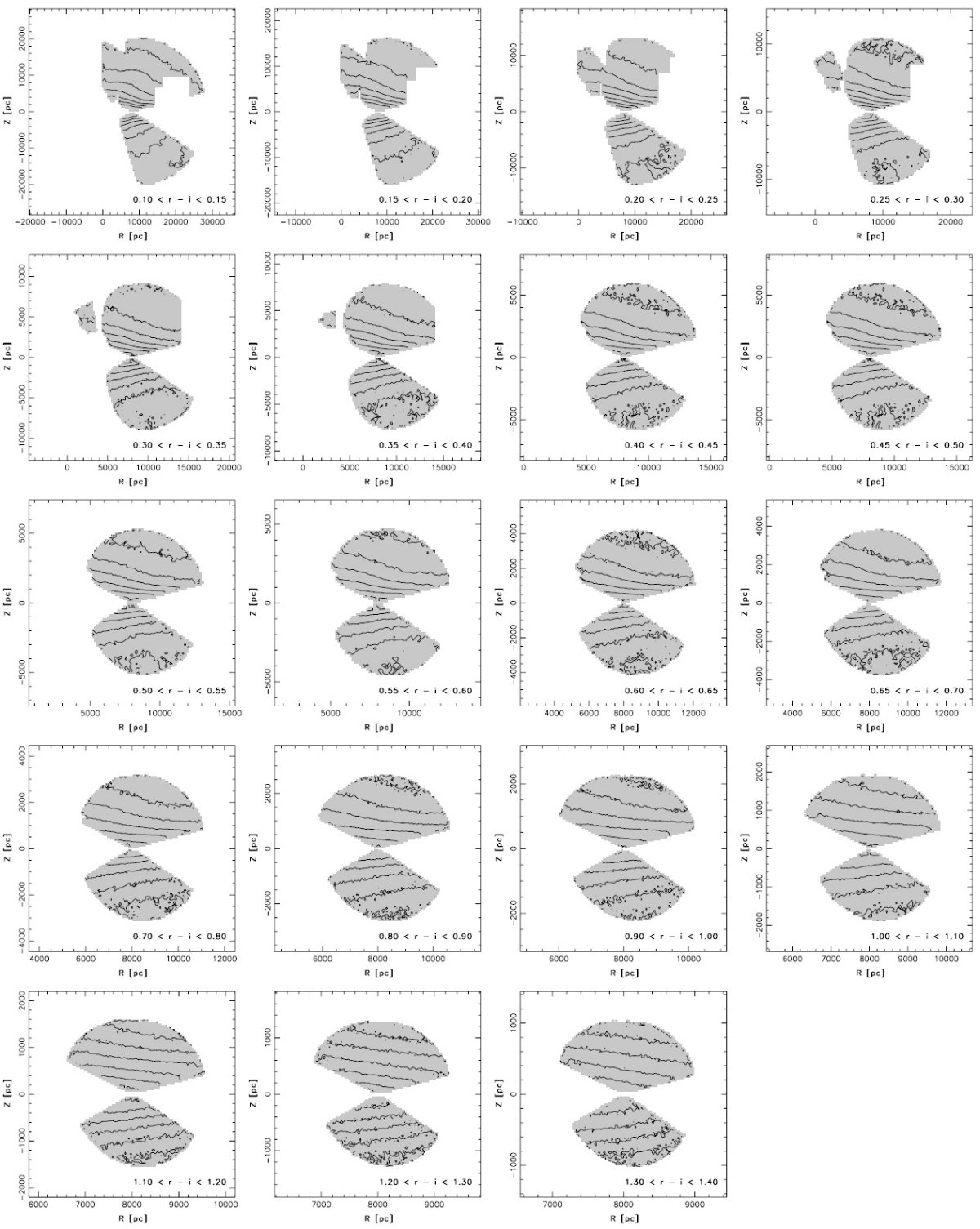
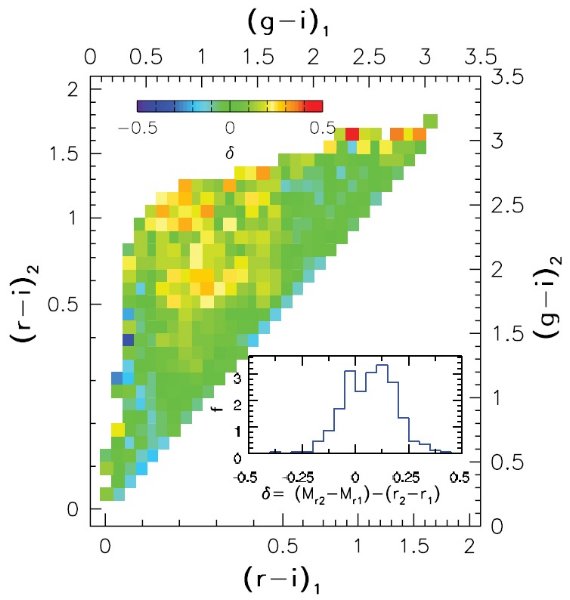
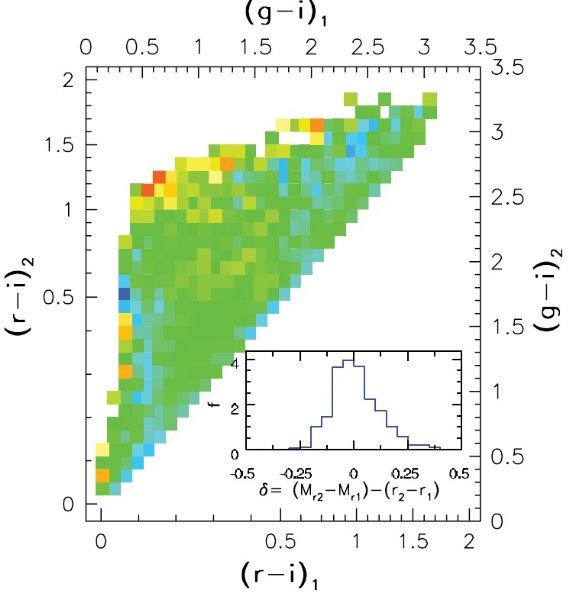
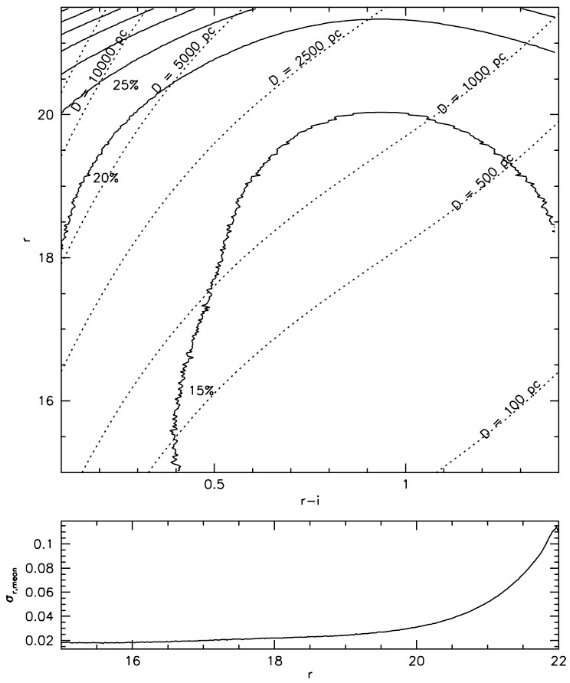
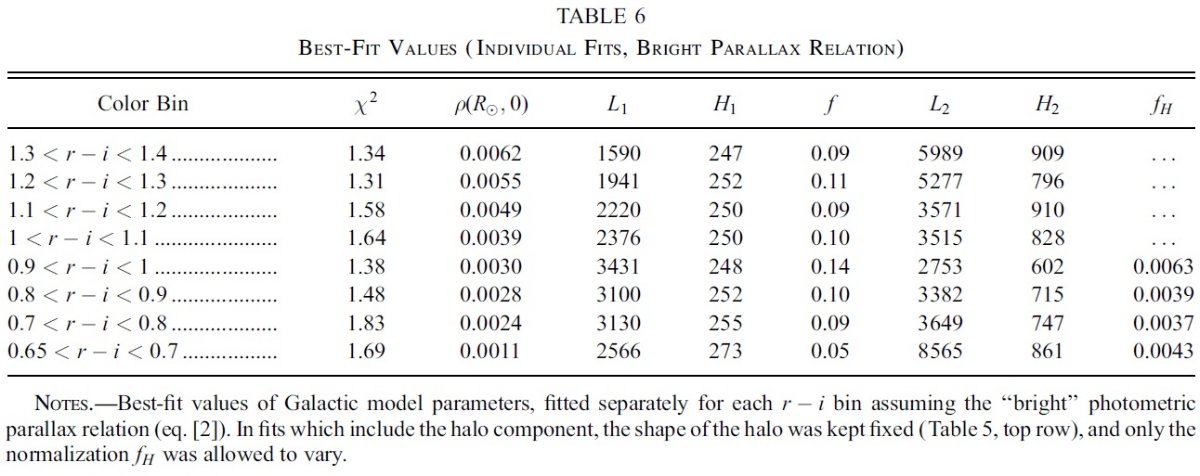
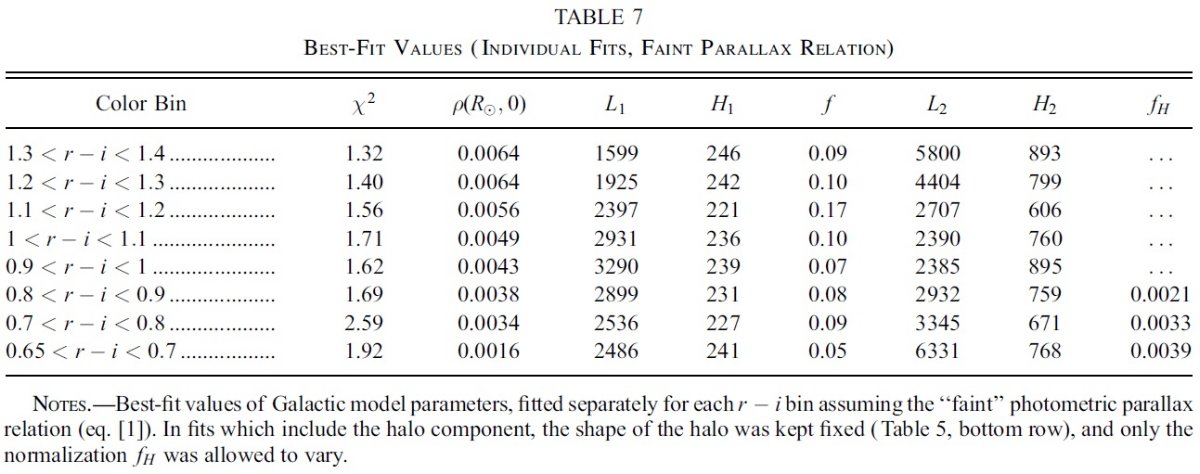
図２． SDSS ugriz システムでの測光視差関係。二つの近似式は、 点線＝明るい規格化、実線＝暗い規格化である。下側の Siegel et al 2002 のラインは低メタル星。黒丸＝ M 13 の SDSS 観測。 　SDSS の測光視差　 　図２にはいくつかの異なるフィルターシステムの観測を SDSS システムで較べた。 それらを次の４次式で近似した。 　　Mr = 4.0 + 11.86(r-i) - 10.7 (r-i)2 + 5.99(r-i)3 - 1.20(r-i)4 　（１） 独立な測光視差として、視線速度と固有運動データに基づいた新しい式を論文３ で提案するが、それは 　　Mr = 4.0 + 11.86(r-i) - 10.7 (r-i)2 + 5.99(r-i)3 - 1.20(r-i)4 　（１） 式（１）を明るい規格化、（２）を暗い規格化と呼ぶ。これらの関係式は勾配 が急で、 青い (r-i) = 0.1 付近で ΔMr/Δ(r-i) = 10 である。 このため、測光には 0.001 - 0.02 という高い精度が要求される。

　２．２．１．メタル量と測光視差　

δ 法　 　メタル量は測光視差の主なる系統誤差の原因である。Carney 1979 は δ 法を提案した。これは UV 超過を用いて測光視差をカラーとメタル量の二つから 決める方法である。この方法を図３のヒアデス星団に適用した結果は満足のいく ものであった。 　δ 法を SDSS 測光システムに応用する可能性が Karaali et al 2005 に より研究されたが、 SDSS の u バンドは完全な AB システムではないため、また メタル量の決定は測光系の差に敏感なため上手く行かなかった。 　Ivezic et al 2006 のメタル量　 　Ivezic et al 2006 は SDSS (u-g) - (g-r) 関係のメタル量効果を調べた。 彼らは SDSS スペクトル (Allende Prieto et al 2006) から導いたメタル量を 用い、(g-r) - (u-g) 面上の星位置がメタル量に強く依存することを示した。 例えば、エクセスが決めやすい青い星 u-g < 1、大部分が F-型星、では 　　　　　[Fe/H] = 5.11(u-g) - 6.33 が分光観測から決めたメタル量を rms = 0.3 dex で再現する。この関係式はこの 最も好適なカラー域でも (u-g) カラーのエラー 0.1 mag が [Fe/H] のエラー　 0.5 dex となり、絶対等級 0.5 mag のエラーを生み出すことを示す。 　ハローの深い探査　 　ハローを遠方まで探査したい。明るい青い星のメタル量を上の方法で決める 際に、 u-等級の精度が問題になる。例えば、u = 20.5 での u-g ランダムエラー は 0.1 mag になる。これは g = 19.5 より明るい星に相当する。従って u-g カラーによるメタル量の決定にはサンプルの限界等級を 2 等以上浅くする という代償を払わなけれなならない。したがって、この論文では、測光視差関係 にメタル量補正を加えずに用い、第５章での大規模ハロー密度超過の扱い でのみ u-g カラーとメタル量の関係の補正を行う。 　測光視差関係式の適用度　 　メタル量は銀河面からの光度の方が動径方向よりも強い勾配を示す。今回は 高銀緯を扱うので、距離と光度がほぼ対応する。用いる関係式の赤い方 は近傍の幾何学的に視差が決まった星のデータを用いている。 SDSS サンプル は M 矮星では 1 kpc までしか届かない。青い方は 10 kpc まで伸びるが、 こちらの測光視差関係は球状星団とハロー星の運動から決められている。従って 結果として使用する測光視差関係式は近傍の赤い高メタル矮星と遠方の低メタル 星に対し実質的に適用可能な形になっている。

図３．測光視差の比較。図２を主系列星の (r-i) = f(g-r) 関係式を使い、 描きなおした。 点線＝明るい規格化。実線＝暗い規格化。破線=Girardi et al. は Mg = 6 に対するモデルカラーの範囲を示す。一点鎖線＝Siegel et al 2002 は低金属 量星。三角＝ 球状星団 Pal 5 ([Fe/H]=-1.4). 白丸＝ ヒアデス([Fe/H]=0.1). 四角＝散開星団 M 48 ([fe/H]=-0.2)。 ３つの黒丸＝球状星団 M 13 ([Fe/H] =-1.5). ヒアデス系列を Laird et al 1988 の処方により M 13 のメタル量に 直した時の一致に注目。参考だが B-V = 0.95(g-r) + 0.2 式の精度は 0.05.

　２．２．２．実視連星を用いた測光視差のテスト　

図４a．間隔が広い連星 17,000 組の δ 中間値の分布。ここで、 (r-i)1 = 主星のカラー、(r-i)2 = 伴星のカラー。 δ = (Mr, 1 - Mr, 2) - (r1 - r1) = (絶対等級の差) - (見かけ等級の差)。 絶対等級の導出に明るい規格化式（２）を使用。

図４b．絶対等級の導出に暗い規格化式（１）を使用。 枠内は δ の分布。

２．２．３．巨星の混入　 　深い探査では巨星混入率は下がる　 　SDSS にも他のサーベイと同様、巨星混入の問題はある。しかし、探査が深い ので、混入率は低い。それくらい低フラックスになると、巨星距離は 100 kpc を越えてしまう。そのような遠方での星密度は低くなり、巨星の寄与率も 下がって行く。 　混入の実際の効果　 　それを定量的に示すのが図５である。混入が最も厳しいのは G-巨星で最大で　 5 % に達する。図５下を見ると、 混入の影響は Z > 500 pc で密度を 一様に　４% ほど上げることである。この距離領域は明るい青い矮星により探査 されている。一方、低高度域は赤い矮星 M-矮星 により探られ、そこでは M 巨星 の混入は無視できる。 　高銀緯では　 　実際、我々が扱っているサンプルには M-矮星が数千万個あるが、M-巨星は 数千個しかない。 　２．２．４．分解できない連星　 　多重星を単一星と看做すと、距離を実際より近く見積もってしまう。その結果、 スケール長やスケール高を最大 35 % 小さく決めることになる。このバイアスは 多重星を構成する星の種類にはあまり依らないが、多重星の割合には依存する。 解析は全ての星を単一星と考えて行った。従って、距離スケールは下限値と 看做すのが妥当である。 　２．２．５．SDSS 主系列星の距離範囲　 　主系列星の測光視差の問題は RR Lyr 20 kpc, M 巨星 100 kpc に較べ、 近距離 までしか到達できないことである。しかし、その良さは圧倒的な数にある。 例えば、 SDSS で MS/RRLyr > 10,000 で MS/Mgiants はさらに大きい。この 結果、密度分布を高い空間分解能と高い精度で決められる。

図５．巨星を主系列星と考えたための影響。上：スケール高 200 pc と 1200 pc の２円盤モデルにおける R = 8 kpc での密度の高度 Z による変化。短破線＝ 円盤。長破線＝べき乗指数 3 のハロー。中：巨星の割合を 5 % とし、誤同定 により距離を 1/3 に見積もった場合の巨星の寄与。下：混入を受けた星密度の 真の密度に対する比率。

　２．３．SDSS 恒星サンプル　

２．３．１．観測　 　２．３．２．星間減光補正のエラーの影響　 　 Schlegel et al. 1998 の減光マップは精度 10 % である。我々はこの減光をサンプル星全てに適用した。 近傍の星にこの減光を当てはめるのは不適当である。どのあたりから全減光適用が 妥当になるのだろう？そのため、赤色矮星の r-i > 0.9 の星を選んだ。これら の星は r-i に関係なく g-r = 1.4 一定値を持つ。調べると、r > 15 の星の g-r 中間値は一定であった。ところが r < 15 の星では g-r が青くなった。 これは、 r > 15 の星は減光層の向こう側にいることを示す。これは距離に 直すと約 80 pc である。そこで、測光距離が 100 pc 以内にある星は銀河モデル から外すことにした。 　２．３．３．反復観測の扱い　 図７．上：距離の相対エラーの (r, r-i) による変化。測光視差関係の固有エラー を σMr = 0.3 mag と仮定。実線＝距離相対エラーの等高線。 σD/D = 15 % から始まり、5 % おきに引いた。

表１．反復観測の統計

　２．３．４．最尤法による星カラーの決定　

カラーと等級　 　測光視差法は絶対等級を求めるために r-i カラーを必要とする。この方法は 青い方では勾配が急で、r-i の小さな誤差でも Mr には大きな誤差となって はね返る。青い星では g-r または u-g を用いる方が良いだろう。一方、 M0 より晩期の星では g-r = 1.4 = 一定となるので、g-r を分類に使うのは無理 である。 　カラーと見かけ等級の最尤値 　図８には (r-i, g-r) 二色図を示す。星の系列は次の式で表される。 　g-r = 1.39{1 - exp[-4.9(r-i)3 -2.45(r-i) -1.68(r-i) -0.050]}　(4) この系列の固有巾は青い方で 0.02 mag, 赤い方で 0.06 mag で、測定エラーより 小さい。そこで、観測カラーのこの系列からのずれは観測エラーと看做す。そして エラー楕円を用いて、最大確率となる (g-r)e, (r-i)e を得る。次に χ2 = (r - re)2 + (g - ge)2 + (i - ie)2 σr σg σi を最小にして最尤値 (ge, re, ie) を求める。その結果は、 re = wrr + wg[g - (g - r)e] + wi[i +(r - i)e] wr + wg + wi 　　　　　ge = (g - r)e + re 　　　　　ie = (r - i)e + re (符号逆？ ) ここに、wj = 1/σj2, j = g, r, i 　系列投影法　 　(r - i)e から式１、２を用いて Mr が得られる。この方法を 系列投影法と名付ける。

図８．48 M 星の (r-i, g-r) 分布。大部分の星は狭い経路沿いに 並ぶ。その幅は明るい g-r < 1 端で 0.02, 暗く赤い g-r - 1.4 で 0.06 mag である。内枠はカラー評価の向上に用いた最尤法を 示す。楕円＝測光エラー。

　２．３．５．クエーサーの混入　

　２．３．６．距離の評価　

　２．４．密度マップを作る　

　３．星数密度マップ　

３．１．円柱座標 R-Z 面での数密度マップ　 　サンプル星の距離範囲　 　我々のサンプル r-i = [0.10, 1.40] は広い距離巾を持つ。カラーを 19 の 区間に分けてそれぞれのカラー区間毎にマップを作った。マップは r-i = 1.3 M 矮星で 100 pc から始まり、 r-i = 0.1 主系列ターンオフでは 20 kpc まで 届く。 赤い矮星　R < 2 kpc　 　図１０下段は赤い星による R < 2kpc の分布が示されている。それは二重 指数関数に極めて良くフィットする。 ρ(R,Z) = ρ(Ro,0) exp ( - R-Ro - Z + Zo ) ここに L = 円盤スケール長、H = 円盤スケール高である。このモデルは等密度 線が次の式で表されることを予想する。 |Z + Zo| = C - H R L ここに C = 定数である。この表式は観測データとよく合う。 　青い矮星　 　青い矮星は図１０の上中段にしめすように上の単純なモデルからの乖離が 目立ってくる。 （１）R > 14 kpc では円盤のフレアが見えてくる。 （２）高度 Z 依存性が単純な指数関数から外れる。付加成分または別関数形 が必要である。 　軸対称性のテスト　 　図１１には R = Ro の円筒壁面上の密度分布を二つのカラー区間の星に対して 示す。完全な軸対称性が成立している場合、等高線は水平になるはずである。 図１１上は r-i = [1.0, 1.1] 区間で、 r-i ≥ 0.35 の星を代表している。 等高線は平行で、軸対称性を示す。しかし、 r-i < 0.35 区間の星は 軸対称性からのずれが存在する。図１１下の図を見ると、銀河面から数 kpc 上で Z = 10 kpc, φ = 40 付近に等高線が上向きになる。これは密度超過の 存在を示唆する

図１１．R = Ro の円筒壁面上での密度分布。上：r-i = [1.0, 1.1]. 下： r-i = [0.10, 0.15]. 等密度線がほぼ水平なのは分布が軸対称 に近いことを示す。それでも、下図で Z = 10 kpc, φ = 40 付近 にずれが見える。 ( φ のゼロ点がどの方向なのか？)

　３．２．３次元マップの X-Y 断面図　

　３．３．全体の密度分布　

上に述べたように密度超過や複雑な構造が見つかったが、銀河系全体での 密度変化は何桁に及ぶのに対し、それらの構造はファクターの違いである。 従って、全体構造に関しては解析モデルによる記述が有効である。そこで 多パラメタ―によるモデル化の前に、R-方向、Z-方向の単純な記述がどの程度 有効かを確認したい。 　３．３．１．数密度分布の Z-依存性　 　Z < 2 kpc は単一指数関数則　 　図１５には R = Ro = 8 kpc での数密度の Z-変化をいくつかの r-i カラー 区間別に示した。上図は赤いカラーの星で Z = 50 pc - 2 kpc 範囲の密度 を示す。それらは明らかに、スケール高 270 pc 指数関数によくフィットする。 スケール高の値自体の精度は 10 -20 % だが、上図で全てのカラー区間データ が全て同一のスケール高でフィットできるのは心強い。 　太陽の銀河面高度　 　Z > 0 と Z < 0 の指数関数フィットを伸ばすと Z = -25 pc で交差 する。これは太陽が銀河面から北銀極方向にずれている効果である。 　厚い円盤　 　より青い星の分布は 1 kpc を越える。１５図中断を見ると、分布が単一指数 関数則から外れていくことが判る。 1 kpc より上方での密度のずれは通常もう 一つの円盤＝厚い円盤の証拠と看做されている。実際中段データは二つの指数 関数の和でフィットされた。 　ハロー　 　 3 - 4 kpc を越すと厚い円盤でさえもフィットしなくなる。図１５下段の データはべき乗則成分の導入によりフィットが可能になることを示す。 図１５．R = 8 kpc での垂直密度分布の r-i カラー区間による変化。フィット した線は指数関数モデル。上図の破線＝スケール高 270pc の単一指数関数。 垂直な一点破線＝密度極大で、太陽位置が銀河面から 20 pc ずれていることを 示唆する。 中図の破線＝スケール高 270 pc と 1200 pc、相対規格化 0.04 (薄い円盤と 厚い円盤)の指数関数モデルの和。一点鎖線＝ 1200 pc 円盤の寄与。この寄与 が効くのは |Z| > 1000 pc であることに注意。 下図データに沿った破線＝スケール高 260 pc と 1000 pc、相対規格化 0.06 (薄い円盤と厚い円盤)の指数関数モデル、べき乗指数 2、薄い円盤に対する 相対規格化 4.5 10-4の楕円体成分の和。破線＝ 260 pc 円盤の 寄与。一点鎖線＝ 1000 pc 円盤の寄与。点線＝ハロー。 ここで示した円盤、ハローモデルは出発点に過ぎず、実際 4.3.9 節の表１０ に示す値はここでの値と全く違う。

　３．３．２． 数密度の R-変化　　

図１６＝赤い矮星　 　図１６には赤い星 ．r-i = 0.70 - 0.80 (K7-M0) 星の Z = 500, 1000, 1500 pc での数密度動径変化を示す。データ点は太陽近傍 2 kpc 以内に限られる。 ln(ρ) - R プロットが直線状に並んでいるのは指数関数型の分布が成立し ていることを示す。スケール高は銀河面高度と共に増大している。データ巾 が短いので L ∼ 3.5 kpc という値を大きく変える証拠にはならない。 　図１７、図１８＝もっと上　 　銀河面高度が 1 - 2 kpc より高くなると、指数関数の近似はデータにフィット しなくなる。その大きな原因は Z = 2 - 8 kpc の一角獣座星流で、データを |Y| < 1 kpc に絞る（図１８）とその影響は著しい。 図１７．r-i = 0.50 - 0.55 (K6), 0.20 - 0.25 (G6 - G9), 0.10 - 0.15 (∼ F9) 星の一定 Z 高度での数密度動径変化。 Z = 3, 6, 9 kpc の３本を示す。破線＝スケール長 3 kpc と 5 kpc (?) でのフィット。

図１６．r-i = 0.70 - 0.80 (K7-M0) 星の一定 Z 高度での数密度動径変化。 Z = 500, 1000, 1500 pc の３本を示す。破線＝スケール長 3 kpc と 5 kpc でのフィット。 図１８．r-i = 0.10 - 0.15 (∼ F9), |Y| < 1 kpc 星の一定 Z 高度 での数密度動径変化。 上段： Z = 2, 3, 4 kpc. 中段： Z = 4, 5, 6 kpc. 下段： Z = 6, 8, 10 kpc. 一角獣座星流は R = 16 - 17 kpc の盛り上がりとして見える。 R = 6 kpc の 幅広の盛り上がり＝おとめ座密度超過である。

　４．銀河系モデル　

前章の定性的な観察から、大規模な構造は解析モデル 　　　ρ(R,Z) = ρD(R,Z; L1,H1) + f ρD(R,Z; L2,H2) + ρH(R,Z) でフィットできそうである。ここに、 ρD(R,Z; L,H) = ρD(Ro,0) exp ( - R - Ro - Z + Zo ) L H ρH(R,Z) = fHρD(Ro,0) [ Ro ] nH SQRT[R2 + (Z/qH)2] 　４．１．データセットのパラメタ―　 　おとめ座密度超過域の排除　 　以下の領域をおとめ座密度超過域として排除する。 ( X′ ) = ( cos 30 - sin 30 ) ( X ) Y′ sin 30 cos 30 Y として、 　　　　　- 5 kpc < X′ < 25 kpc 　　　　　Y′ > -4 kpc 　　　　　(X-8kpc)2 + Y2 + Z2 > 2.5 kpc2 これは図１９上段の白枠部分である。 　一角獣座星流の排除　 　一角獣座星流は銀河中心からほぼ等距離にある。排除域は以下の式で定める。 　　　　　14 kpc > R > 24 kpc, 0 > Z > 7 kpc または、 　　　　　16 kpc > R > 24 kpc, 7 kpc > Z > 24 kpc この領域は図１９下段の二つの白枠である。　 　あと二つ密度超過があった　 　上の二領域を除いた後の r-i > 1.0 データに第１フィットを行った結果、 H1 = 280 pc, H2 = 1200 pc を得た。残差を見ると、 40 % の密度超過が (R, Z) = (6.5, 1.5) kpc, (9, 1) kpc 付近に見られる。 そこで、 -90 < arctan ( Z - 0.75 kpc ) < 18, 　Z > 0 R - 8.6 kpc 　　　　R < 7.5 kpc, 　Z > 0 も追加排除した。 　追加排除規定　 　こうした後に残ったピクセルを銀河中心極角 φ で ("polar angle" は少し変じゃ ないか？) 平均して図１０のような (R, Z) マップを作った。さらに追加で、b < 20 の銀河円盤に近く減光の強い可能性のある星も排除する。その他、例えば |Z| > 2.5 kpc 星もハロー星混入を防ぐため排除するなどいくつかの排除規定 を設けた。 　図２０＝掃除済みマップ　 　図２０には 19 のカラー区分毎に「掃除済みマップ」を示す。図１０と較べ ると、等密度線がより規則的である。特に赤い r-i > 0.7 (K7 より晩期) では驚くほどきれいである。0.10 < r-i < 0.15 (∼ F9) では ずれが大きくなる。これが軸対称からのズレなのか、距離決定のエラーに 起因するかまだ不明である。

図１９．銀河系解析モデルフィットに使用しない密度超過領域。上段： Z = 10 kpc X - Y 図。白枠部はおとめ座密度超過を避けるため排除。下段: R - Z 図の二つの白枠は R = 18 kpc の一角獣座星流。

　４．２．モデルフィット　

４．２．１．フィットのアルゴリズム　 　outlier = 外れ値の排除　 　モデルフィットはニューメリカルレシピ―にある Levenberg-Marquardt 非 線形 χ,sup>2 極小化アルゴリズムによって行う。フィットと残差 が σN 以上の outlier = 外れ値の排除を繰り返す。 σi = {50, 40, 30, 20, 10} で次第に小さな外れ値を 除く。 　４．２．２．太陽位置　 　使用データ　 　最初のモデルは薄い円盤のみを扱うので、|Z| < 300 pc の星のみを扱う。 また、減光補正の誤差による過ちを避けるために |Z| < 100 pc の星は はじく。また 7.6 kpc < R < 8.4 kpc 領域の外側の星も、デコボコ 構造による混入を避ける意味ではじく。 　太陽位置　 　こうして、太陽の銀河面高度として、以下の値が得られた。 　　 　　Zo, bright = (25±5) pc 　　　　　Zo, faint = (24±5) pc この値は、 Chen et al 1999 の Zo = (27.5±6) pc などと一致する。 表３．明るい測光距離較正による円盤のベストフィットパラメタ―

４．２．３．円盤のフィット　 使用カラー区間　 　r-i > 1.0 の４つのカラー区間からの R-Z 密度分布マップを用い、二重 指数関数モデルをフィットした。カラー区間のデータは薄い円盤と厚い円盤 の星で、ハロー星の混入は 1 % 以下である。その上、このカラー範囲のカラー 等級関係は円盤矮星で較正されているので円盤パラメタ―の決定には好適である。 　一括解析のパラメタ―　 　４つのカラー区分データを一括に解析した結果と、それぞれのカラー区分 毎に解析した結果とを比べた。一括フィットでは ρ(Ro, 0) のみが各 区分で自由パラメタ―となり、スケール高、スケール長、f = 厚い円盤と薄い 円盤の相対比、は共通の値を強制される。ここでのカラー区分に対応する 星の質量、年齢、メタル量はほぼ同じと考えられるので、分布プロファイル が同じと言う仮定には十分合理性がある。一括モデルのベストフィット値は 表３、４の第１行にある。図２１には reduced χ2 等高線 を示す。 表４．暗い測光距離較正による円盤のベストフィットパラメタ―

４．２．４．ハローモデルのフィット　 　ハローは青い星で調べる。 　r-i < 1.0 (M1 より早期)の星はより遠方の領域に到達する。ハロー星が 到達域の端に現れてくる。図１５の中断と下段から分かるように、円盤だけの モデルでは Z ≥ 4 kpc ではフィットが悪くなる。 　フィットの前に考えるべきこと　 （１）ハロー内の塊りやマージャー残存物を事前に除くことが必要である。 そうしないと、モデルパラメタ―が適切に決まらない。　 （２）　測光視差関係には Z 依存性が明示的には含まれていない。 しかし、暗く赤い高メタル円盤矮星は近距離の較正に使われ、 低メタルハロー星は青い側に位置しているので、メタル効果が暗黙の裡 に含まれている。その結果、r-i = 0.15 付近は低メタル [Fe/H] ≤ -1.5, r-i ≥ 0.7 では高メタル [Fe/H] ≥ -0.5 となっている。したがって、 ハロー星の形やスケールを調べるには青い端の星、円盤の形やパラメタ― には赤い端の星が要る。同じ理由で、中間カラーの星を使って、ハローと 円盤を同時にフィットするのは困難である。 　使用データ範囲　 　したがって、ハローの形状を調べるには r-i = [0.1, 0.25] 星を用い、 取り敢えずの qH = 0.5, fH = 0.001 ハローモデル で、(R, Z) 面上円盤星の割合が 5 % 以下の領域のみを扱う。このデータ から、べき乗指数 nH, と軸比 qH が決まる。 円盤をデータから排除しているから、fH は決まらない。 　ハローパラメタ―の決定は緩い　 　ハローのベストフィットパラメタ―を表５に示した。図２２には カイ二乗の等高線を示した。円盤に比べるとフィットは悪く、reduced χ 2 = 2 - 3 である。形式的には nH = 2.8, qH = 0.64 が極小点であるが、reduced カイ二乗の大きさと 浅い極小点を考えると　nH = 2.5 - 3, qH = 0.5 - 0.8 と緩く考えるべきである。 　密度超過　 　図２３には、最も赤いカラー区分で決めた厚い円盤と薄い円盤のベスト フィットモデルに４種類のハローモデルを足した結果とデータとの残差を 最も青いカラー区分サンプルについて求めたものである。一角獣座 R = 6.5 kpc とおとめ座 Z = 1.5 kpc の密度超過は明らかであるが、その細かい形 はハローモデルパラメタ―の選択で変わる。また、うんと外側ではフィット が常に過剰か不足になるのは二重ハローの必要性を示している。しかし、 オブレートな形状が必要なことは確かである。

表５．ハローの形のフィット。 図２２．データベストフィット点周りの (nH, qH) 面上での還元（？）χ2 等高線。表５第１行。 最内側の等高線は 1.1 χmin2 。残りは log χ2 で 0.5 から 0.5 区切り。

　４．２．５．円盤とハローの同時フィット　

　４．３．解析　

　４．３．８．ベストフィットからの残差の統計　

図２８．(R, Z) 面上での残差強度分布。黒線ヒストグラム＝データ。 実線＝ガウシャンフィット。 図３０．r-i = [0.10, 0.15] 星の Z = 10 kpc X - Y 面分布。円盤成分の寄与 が 5 % 以下のピクセルのみを示す。図の色はノイズで規格化されており、 -3σ = 紫と3σ = 赤で飽和させた。上図の大きな赤部分はおとめ座 密度超過が原因である。この密度超過域はフィットでは排除されている。

図２９．左列：３つのカラー区間に対し、(X, Y, Z) ピクセルでのポアソン ノイズ規格化残差の分布。 右列：モデルで規格化した残差の分布。 黒線ヒストグラム＝データ。赤点線＝残差からポアソンノイズだけ考えた際の 分布。 最下行：モンテカルロで作った擬カタログから作った分布。 省略

４．３．９．広域探査領域とパラメタ―縮退　 　一意性の問題　 　１０ものフリーパラメタ―があるモデルではパラメタ―間の相互作用や解の 一意性を理解することは難しい。そこで２つの例を示す。 　図３１の例　 　図３１は２つのモデル、一つは薄い円盤＋厚い円盤、もう一つは円盤＋ハロー、 を比べた。大きく異なるモデルだが、 R = 8 kpc での Z 分布は殆ど同じに パラメタ―を調整できた。 　図３２の例　 　図３２の左には図１５の上２図を示す。密度分布は２つの指数関数円盤の 重ね合わせで良く再現されている。図３２の右にはデータに表３のベスト フィットモデルを重ねた。左は H1 = 260 pc, H2 規格化＝ 4 %, = 1000 pc, 右は H1 = 245 pc, H2 = 750 pc, 規格化 = 13 % である。パラメタ―は大きく異なるが結果は良く似ている。 　縮退の実験　 　上の例は一般にペンシルビームサーベイに付きまとう問題で、領域が 狭い場合にも生じる。我々は似たような χ2 を生じるモデルの 体系的な探索は行っていないが、ランダムに選んだ 100 組の初期値からベスト フィットを求める実験を行った。個々の "individual bins" (カラー区間のこ とと解す）でフィットした場合には局所的な χ2 極小 に捕まる。それらは全体の最小 χ2 の 20 - 30 % 大きい。 そしてそのパラメタ―値はベストフィットと大きく異なる。一方、一括解析 した場合には、（１）収束に失敗、（２）最小値の数倍大きな局所極小に 収束、（３）同じベストフィット極小に収束、のどれかだった。SDSS データ はこうして、領域の狭さから来る縮退からは免れているようである。

図３１．フィッティング主体の例。上：薄い円盤＋厚い円盤でハローなしの モデル。中：一枚円盤＋平たいハローモデル。どちらも R = 8 kpc, |Z| < 8 kpc でほとんど同じカウントを示すようにパラメタ―調整した。 下：二つのモデルの差。対数表示。ゼロレベルは緑。両モデルは |Z| > 3 kpc と R が 8 kpc から離れた所でのみ差が生じる。

４．３．１０．円盤とハローを別個成分とする物理学的理由　 　u-g とメタル量　 　観測範囲が遠方まで及ぶにつれ、銀河系構成要素の数が増していく。これらは 本当に物理的に異なる系なのか、それとも物理的な裏付けのない現象論的な 記述上の区別に過ぎないのだろうか？数密度のみではこの問いに答えることは 出来ない。円盤星＝種族Ｉ＋中間種族ＩＩはハロー星に較べメタル量が　1 - 2 dex 高い。この差により、ターンオフ星の u-g カラーは大きく変わる。Kurucz モデルによると、ターンオフで u-g = [0.7, 1.0] にある星はメタル量が -1 dex 低い。 　u-g の差が空間分布に反映　 　r-i = [0.1, 0.15] サンプルを u-g = [0.60, 0,95] と [0.95, 1.15] に分ける。これで円盤星とハロー星を近似的に分けられる。 図３３を見ると、２つのグループははっきり異なる空間分布を示す。 この現象は図１５に採用されたような複数成分モデルはデータの過剰解釈では ないことを示す。しかし、ここで示されたデータのみでは円盤とハローの 必要性は確認できても、厚い円盤と薄い円盤の分離に物理的な差は付け加え られない。

図３３．r-i = [0.10, 0.15] 星の R = 8 kpc における Z 分布。 星は u-g （メタル指標）でグループ分けして表示した。丸は　 u-g = [0.60, 0.95] 低メタルハローサンプル。三角 は　u-g = [0.95, 1.15] 高メタル円盤サンプル。上図のラインは２つのサブ サンプルの和。２つのサブサンプルは中図と下図に示す。 単純な区分けのため、円盤星は |Z| > 5 kpc でハロー星の、 ハロー星は |Z| < 2 kpc で円盤星の汚染を受けている。

　４．３．１１．補正されたベストフィットパラメタ―　

円盤サンプル　 　４．２．節では円盤をフィットするのに、 r-i = [1.0, 1.4] の M 型矮星 と r-i < 1.0 の　K-型、早期 M-型矮星の２つのサンプルを使った。 ベストフィットのパラメタ―は両サンプルで一致し、２つの指数関数型円盤 に分布することを示した。 　r-i = [1.0. 1.4] カラー区間が円盤向き　 　r-i = [0.65, 1.0] サンプルへのフィットは第３成分＝ハローの必要性を 示唆した。しかし、これはこのカラー区間の等級視差関係を低メタルハロー 星に適用してよいか、密度超過の差引残差によるバイアスが残っていないか などの問題がある。そこで、r-i = [1.0. 1.4] カラー区間の星を円盤パラメ タ―決定には採用する。このカラー区間はハロー星の影響がなく、 密度超過の影響もあまり受けない。 　ベスト解の不定性　 　限られたサンプルと知識の下ではベスト解を求め、それらの不定性が及ぼす 影響を考える以外の途はない。明るい測光視差関係を採用する理由は、それが 運動学データと整合する結果を与える（論文３）からである。 表１０．銀河系モデルの最終パラメタ―

連星率の問題　 　様々な連星率の シュミレーションの結果ではその形は r-i > 0.5 では 0.1 mag よりよい。 図３４には連星率によりベストフィットパラメタ―がどう影響されるかを示し ている。 (前にも述べたが、測光視差関係 の方は fm の効果を入れるのか？) 正しい連星率の決定は難問である。その値はまた、スペクトル型で変化する 可能性がある。この論文では、パラメタ―の決定に r-i > 1 の M-矮星を 使用していることを考慮して、 Reid, Gizis 1997 が晩期型矮星に与えた 35 % を採用する。 　パラメタ―の補正　 　こうして、 L1, H1, H2 に対して 15 % 増加、 L2 は 10 % 増加という連星率による補正を与えた。そこに さらに 5 % のマルムキストバイアス補正を加える。それと同じ理由で密度規 格化の方は -10 % となる。こうして決まった最終パラメタ―値を表１０に 示す。 図３４．未認識連星率がフィットに及ぼす効果。計算は表８で行ったもの。各枠には 連星率が変化した時にモデルパラメタ―がどう変わるかを示す。

　５．おとめ座密度超過　

　５．１．おとめ座密度超過の広がりと形状　

　５．２．おとめ座密度超過の直接検証　

天球上の分布図　 　図３７には北銀河系における g-r = [0.2, 0.3], r = [20, 21] 星の分布を ランベルト法で示す。カラーと等級の範囲は D = 18 kpc 付近の星を選択して いる。おとめ座密度超過が (l, b) = (300, 65) 付近で顕著である。 　ヘス図　 　図３７の右側には (l, b) = (300, 60), (60, 60) 方向のヘス図を示す。 左下はその２つの差分である。差分図には g-r = 0.3, r ≥ 20 での強い 超過が認められる。図３８はこの差分を定量的に解析したものである。 赤い星では、両領域のカウントに差は見られない。一方、青い星ではカウント の差は統計的に有意である。青い星のカウントに反転は見られないので、 おとめ座密度超過は SDSS 限界等級の先に伸びていることが窺える。 このように、ヘス図からは、(300, 65) 方向の超過が r = 18 から 21.5 へと 広がることを確認した。 　表面輝度　 　図３７左下の差分ヘス図を使って、密度超過の表面輝度を見積もって みよう。g-r = [0.2, 0.8], r = [18, 21.5] の星を対象とする。この 範囲の星の総計は、 　　　　　Σr = 32.5 mag arcsec-2 ] となる。この値はサジタリウス矮小銀河北側星流の ΣV = 31 mag arcsec-2 より 1.5 等暗い。 　密度超過の総光度　 　密度超過が 1000 deg2、距離 10 kpc, として、全体の r 絶対 等級は Mr = -7.7 mag, 総光度 Lr = 0.09 106 Lo である。 　３．５．おとめ座密度超過のメタル量　 　u-g でメタル量を分離する方法は (g-r, u-g) 面での分離により精度を増す。 　　　　　P1s = 0.415(g-r) + 0.910(u-g) - 1.28 　　　　　P2s = 0.545(g-r) - 0.249(u-g) + 0.234 を使うと、 　　MS:　　-0.06 < P2s < 0.06 　　低メタルターンオフ: -0.6 < P1s < -0.3 で、P1s = -0.3 はほぼ、[Fe/H] = -1.0 に対応する。 　図３９には P1s - r ヘス図を、おとめ座密度超過域、比較域、 差分の３つに対して示した。P1s < -0.3 で大きな超過がある が、P1s > -0.3 には統計的に有意な差は存在しない。この 図は密度超過を形成する星のメタル量は厚い円盤星のそれより低く、ハロー 星に近いことを示している。

図３８．図３７左下の差分ヘス図の定量解析。左列はおとめ座密度超過を 代表する g-r = [0.2, 0.3] カラー区分サンプル、右列は g-r = [1.2, 1.3] カラー区分の比較サンプルである。上＝差分そのまま。中＝相対比で表した 差分。 右中図の差込枠は r < 21.5 mag 星のカウント比。 下＝ポアソン散布で規格化した差分。赤い星ではカウントが区別できないくらい 小さく、青い星では差分が有意に大きい。

　６．議論　

　６．１．パラダイムシフト　

　６．２．ベストフィットモデル　

以前の研究との比較に入る前に　 　表１０には指数関数型円盤モデルを採用した場合のパラメタ―を載せた。 以前の研究との比較に入る前に、様々な効果、特に連星率がモデル作成の際に 考慮されているかどうかが不明な場合、それらの影響が大きいので比較自体が 無意味になる可能性があることを注意しておく。以降では各研究ではそれらの 効果は考慮されていると仮定して比較を進める。 　円盤のスケール高　 　我々が得た薄い円盤のスケール高 300 pc は連星率 35 % を仮定して得た。 この値は標準的な値 325 pc より約１割小さいが、最近の研究、Robin et al 1996, Larsen,Humphreys 1996, Buser et al 1999, Chen et al 2001, Siegel et al 2002 が採用した値 240 - 350 pc の中ほどに位置する。 　厚い円盤のスケール高 900 pc も Siegel et al 2002, Buser et al 1999, Larsen, Humphreys 1996 などの値とほぼ一致するが、 Robin et al 1996, Ojha et al 1999, Chen et al 2001 の 580 - 790 pc より 20 % 大きい。 　厚い円盤の規格化　 　厚い円盤の規格化は 12 % で以前の研究の結果より大きいが、最近の Chen et al 2001, Siegel et al 2002 の 10 % 以上という結論とは整合する。 規格化が　10 % 以下になると χ2 の値が大きくなる。 特に、初期モデルに特徴的な "低い規格化＋高いスケール高" の組み合わせ、 Gilmore, Reid 1983, Robin, Creze 1986 Yoshii et al 1987, Yamagata, Yoshii 1992, Reid,Majewski 1993 は SDSS データからは全く 推奨されない。これ等の研究の基本的な共通点はシングルビームサーベイ、 通常は北銀極、に準拠していることである。しかし、１本または数本の 視線方向では４．３．９．節で述べた多パラメタ―モデルに固有な縮退を 解くには不足である。それらのパラメタ―は局所極小に陥っていて、 銀河系全体の記述には不足なのである。 スケール長　 　薄い円盤のスケール長 2.6 kpc は最近の Ojha et al 1999, Chen et aal 2001, Siegel et al 2002 と合致し、伝統的な 3 - 4 kpc より短い。厚い円盤の スケール長 3.6 kpc は薄い円盤のそれより大きい。全体としては厚い円盤に 含まれる K-, M-矮星の質量、光度は全体（厚い、薄い円盤、ハロー）の 23 % であり、横向き銀河での値 Yoachim, Dalcanton 2006　と大体一致する。

図４１．右上枠：実線＝薄い円盤の等密度線。点線＝厚い円盤の等密度線。 (銀河中心周りが低密度になって いる！ ) モデルパラメタ―は表１０より。R = 8 kpc 付近の２つの四角枠＝銀河系 モデルの円盤パラメタ―を決める観測データが得られた領域。 下図：与えられた R の外側の円盤累積質量比。 左図：|Z| > Zgiven の円盤質量の相対比。 Z 方向のデータは十分に深いが、 R 方向には円盤質量の 20 % 程度しか 含まれていない領域のデータからの外挿であることに注意。

　６．３．円盤内副構造の検出　

　６．４．ハロー　

　６．５．おとめ座密度超過　

　６．６．将来のマップ