Optical Properties of Some Terrestrial Rocks and Glasses


Pollack, Toon, Khare
1973 Icarus 19, 372 - 389



　アブストラクト　

　5 種類の自然石の光学定数を 0.2 - 50 μm で決めた。 ビアーの法則とフレネルの屈折の式を用いて、反射率と透過率の測定の 組み合わせから、0.2 - 5 μm では屈折率の実部と虚部を決めた。 　5 μm より長波長側では反射率の測定しかできなかった。従って 光学定数の決定は分散式を用いて行った。これらの光学定数は岩石表面、 大気中のちり、惑星間及び星間空間ダストと光との相互作用の研究 に役立つ。

　サンプル　

　試料　

　リトルグラス・マウンテン、カリフォルニアとレイクカウンティ、オレゴン の黒曜石と、玄武質ガラス、玄武岩、安山岩の計５サンプルを厚さ１ｃｍの 板に切り取り、次に厚さ 30, 100, 300, 1000 μm の薄片にした。

　測定　

　キャリー１４双光束型分光光度計を用い、 0.2 - 2.5 μm の, パーキン エルマー光度計で 2.5 - 50 μm での反射スペクトルと透過スペクトルを測 った。 		　反射計　

　赤外反射計はバーンズエンジニアリング製でパーキンエルマーに 組み込んで、垂直方向から 11 度傾けた反射光を、標準ミラーとの相対比で測 定した。標準ミラーは 2.5 - 50 μm で 96 % 反射率を仮定した。キャリー １４用反射計は ハルトマン、ロゴセティス 1964 作製のものを用いた。これは 垂直から 13 度の反射を測る。

　測定エラー　

　パーキンエルマーは 30 - 50 μm で波長が圧縮される。このため、この 波長域のスペクトル検出が困難となる。キャリー１４は 0.7 - 2.5 μm で 測定が乱れる。これはサンプルの散乱光のためと思われる。この波長域のデータ は外挿値を用いた。



表１．サンプルの化学組成

　光学定数　0.2 - 5 μm　

　ビアーの法則　

　R = 表面反射率、k = 吸収係数、ks = 散乱係数、 t = 試料厚み と する。入射強度 Io と出射強度 I との関係はビアーの法則で以下の通り。

　　　I = Io(1-R)2exp[-4π(k+ks)t/λ]

対数を取って、
log10 Io = a = 4π(k+ks) t - 2 ln(1-R)
I ln10


厚み t に対して対数透過率をプロットする。その勾配から (k+ks) が決まる。 ks=0 と仮定して、求めた k を表２に示す。

　吸収強度の差　

　吸収係数 k は石とガラスとで大きく異なる。安山岩と黒曜石の間では k が 二桁異なるし、黒曜石同士でも一桁差がある。黒曜石に見られる 2.8 μm の吸収帯はおそらく鉱物中の水であろう。

　フレネルの式　

　吸収係数 k と垂直反射率 R が分かると、屈折率 n は下のフレネルの式を 用いて導かれる。
R = (n-1)2 + k2
(n+1)2 + k2


n の値は表２と図１に示されている。二つの黒曜石の屈折率、玄武岩と安山岩 の屈折率は似ているので、図にはレイクカウンティの黒曜石、玄武岩、玄武ガ ラスのみを示した。

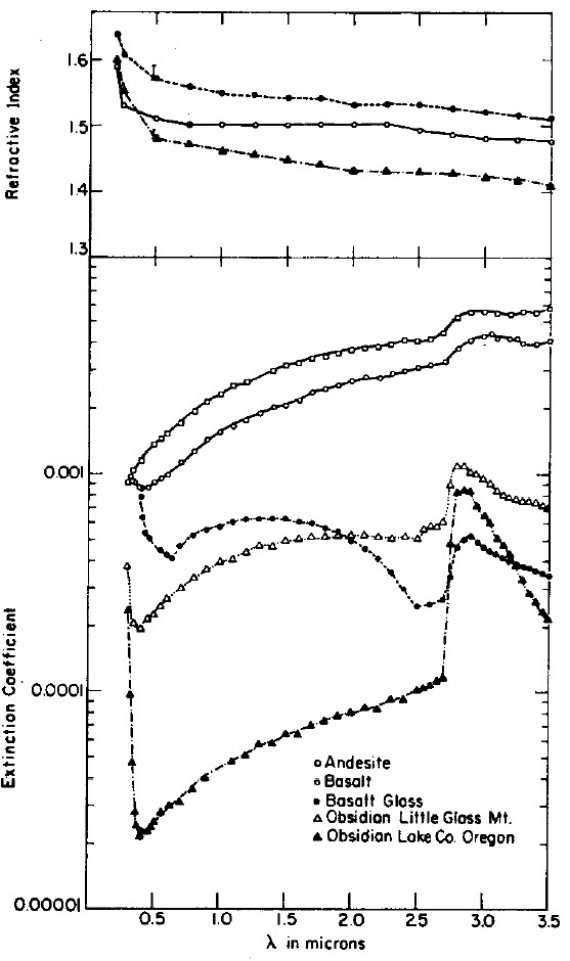図１．λ = 0.2 - 3.5 μm での光学定数。安山岩と黒曜石の屈折率は クラリティのため省いた。0.5 μm 付近での黒曜石と玄武岩の屈折率に着けた 縦棒は Becke Line の測定。 　

表２．サンプル光学定数








　光学定数　5 - 50 μm　


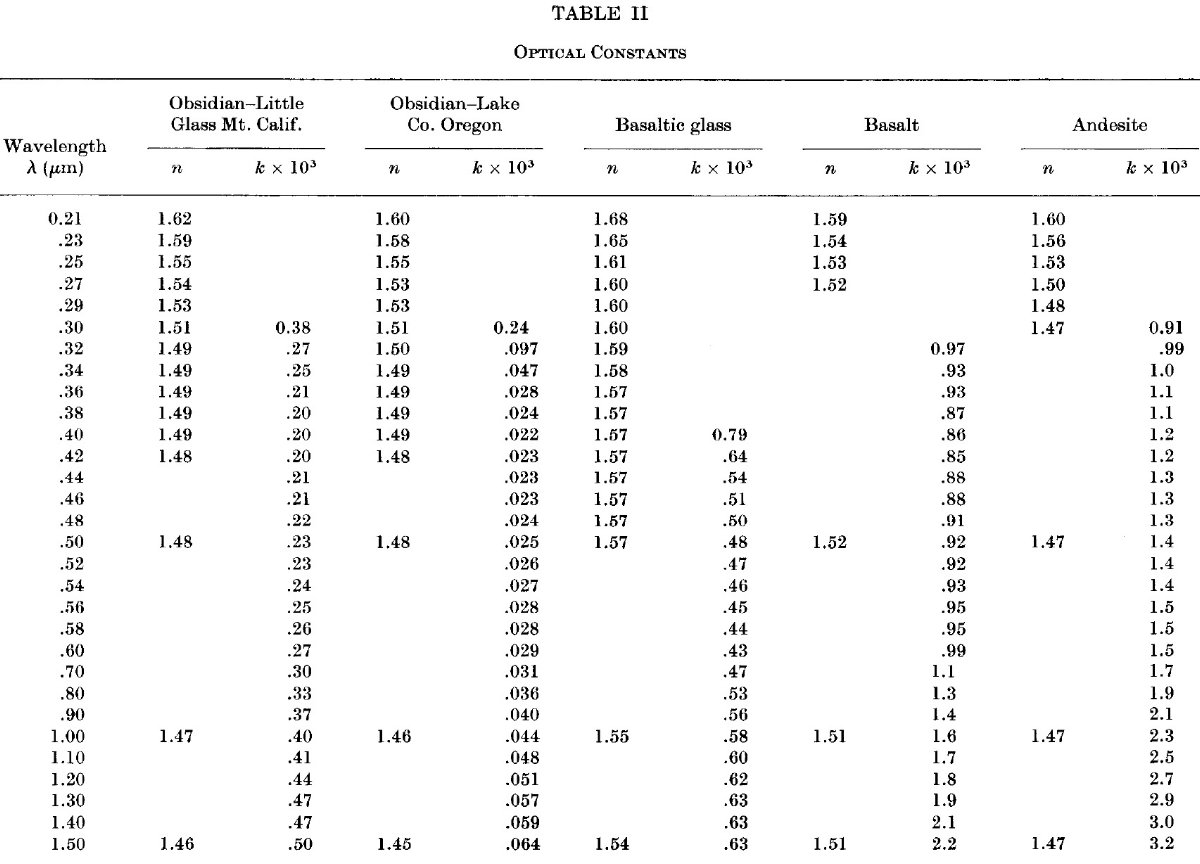
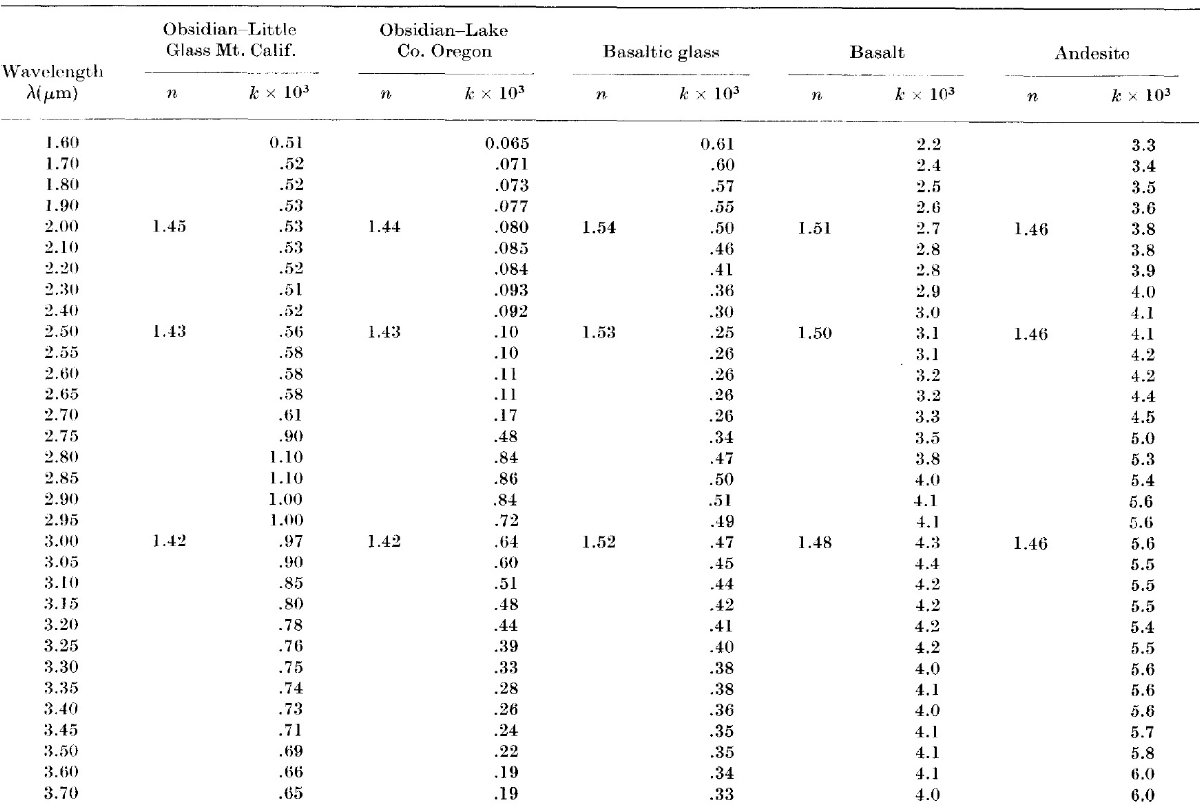
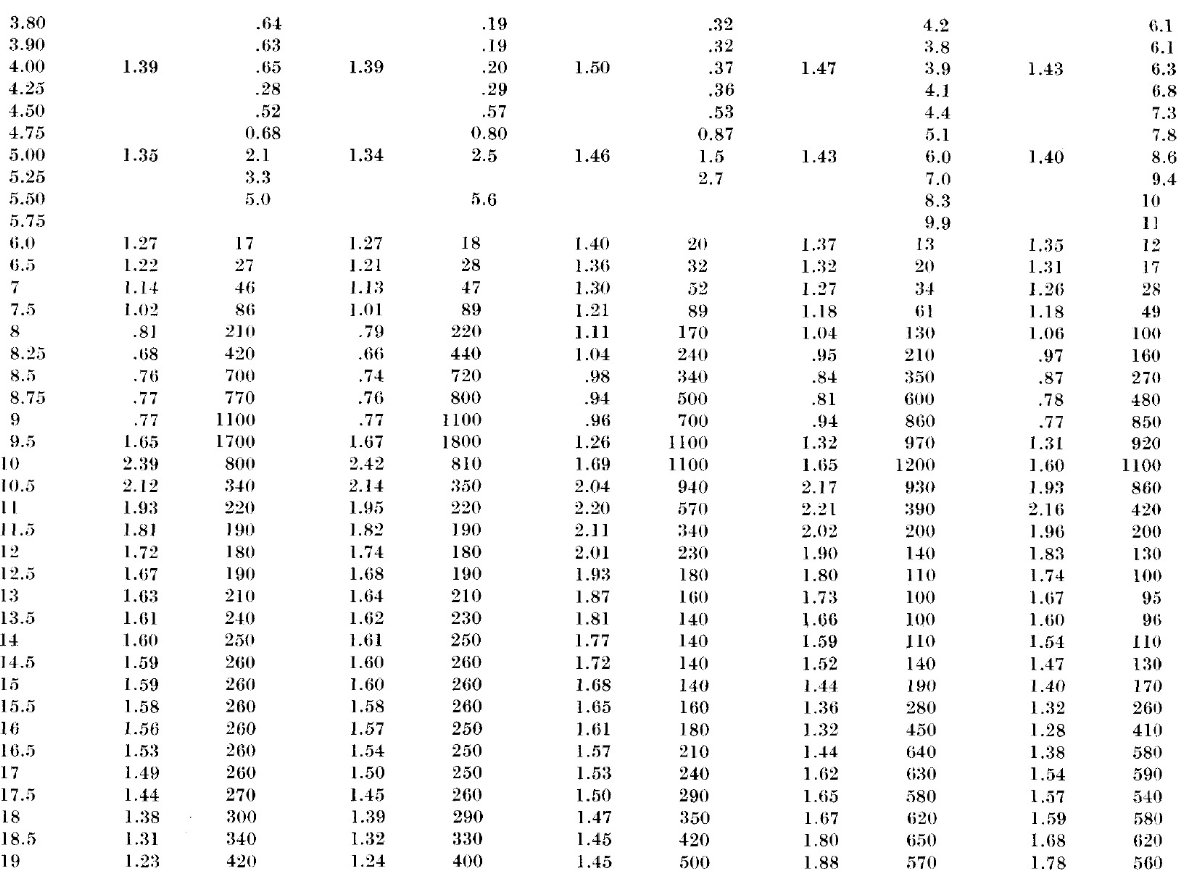
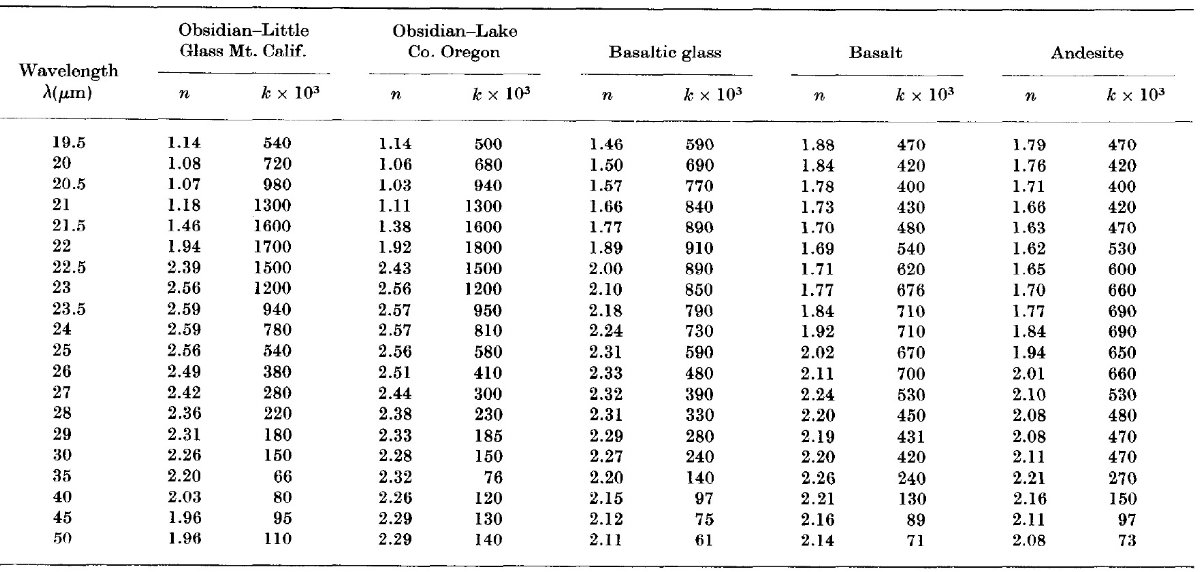
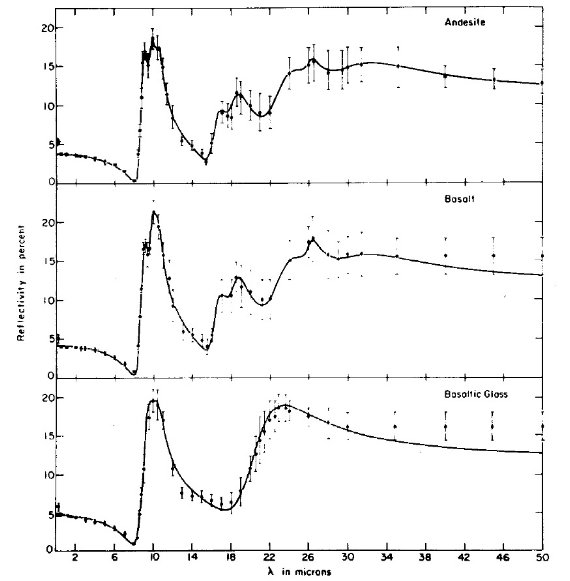図２．安山岩、玄武岩、玄武ガラスの分散式解析結果。黒点＝測定反射率。 実線＝分散関係から計算した反射率。

　反射測定だけで光学定数　

　λ > 5 μm では透過率測定精度が低いために、反射率のみから 光学定数を定めなければいけない。そのための方法は幾つかあるが、ここでは 分散式解析を用いる。

　一振動子モデル　

　Hansen, Pollack 1970 は簡単化した一振動子分散式モデルを提案した。 これにより、誘電率短波長定数 A と振動子の３パラメタ― λ0, Γ, 強度 P の１次近似値を決めることが出来る。
nk = P(Γ/2)2
(Δλ)2 + (Γ/2) 2


n2 - k2 = A2 + PΓΔλ
(Δλ)2 + (Γ/2) 2
　

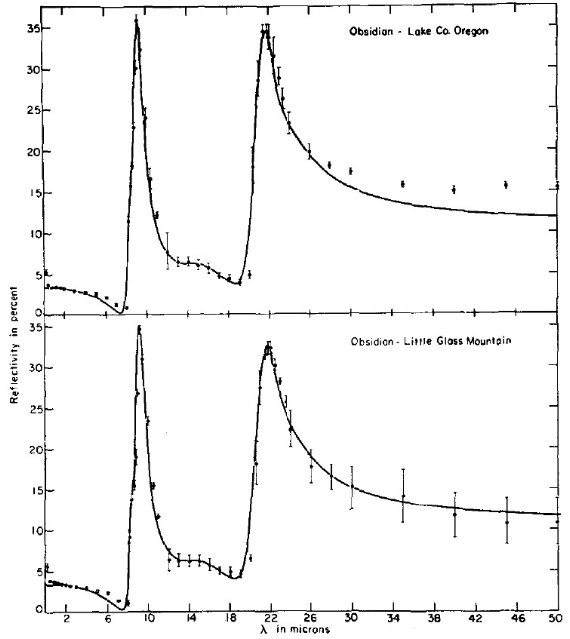図３．黒曜石の分散解析。黒点＝測定反射率。 実線＝分散関係から計算した反射率。

　多振動子モデル　

Spitzer, Kleinman (1961) の多振動子モデルは次のようである。
nk = Σ PjΓj2 λ3 1
j λj (λ2-λj2 )2 + Γj2λj 2


n2 - k2 = A2 + Σ 2PjΓj λ2(λ2 -λj2)
j λj (λ2-λj2) 2 + Γj2λ2


　フィット結果と測定との反射率の比較　

　この式でから予想される反射率と測定された反射率の比較を図２と図３に示す。 分散式のパラメタ―は表３に載っている。



表３．岩石サンプルの分散解析パラメタ―。


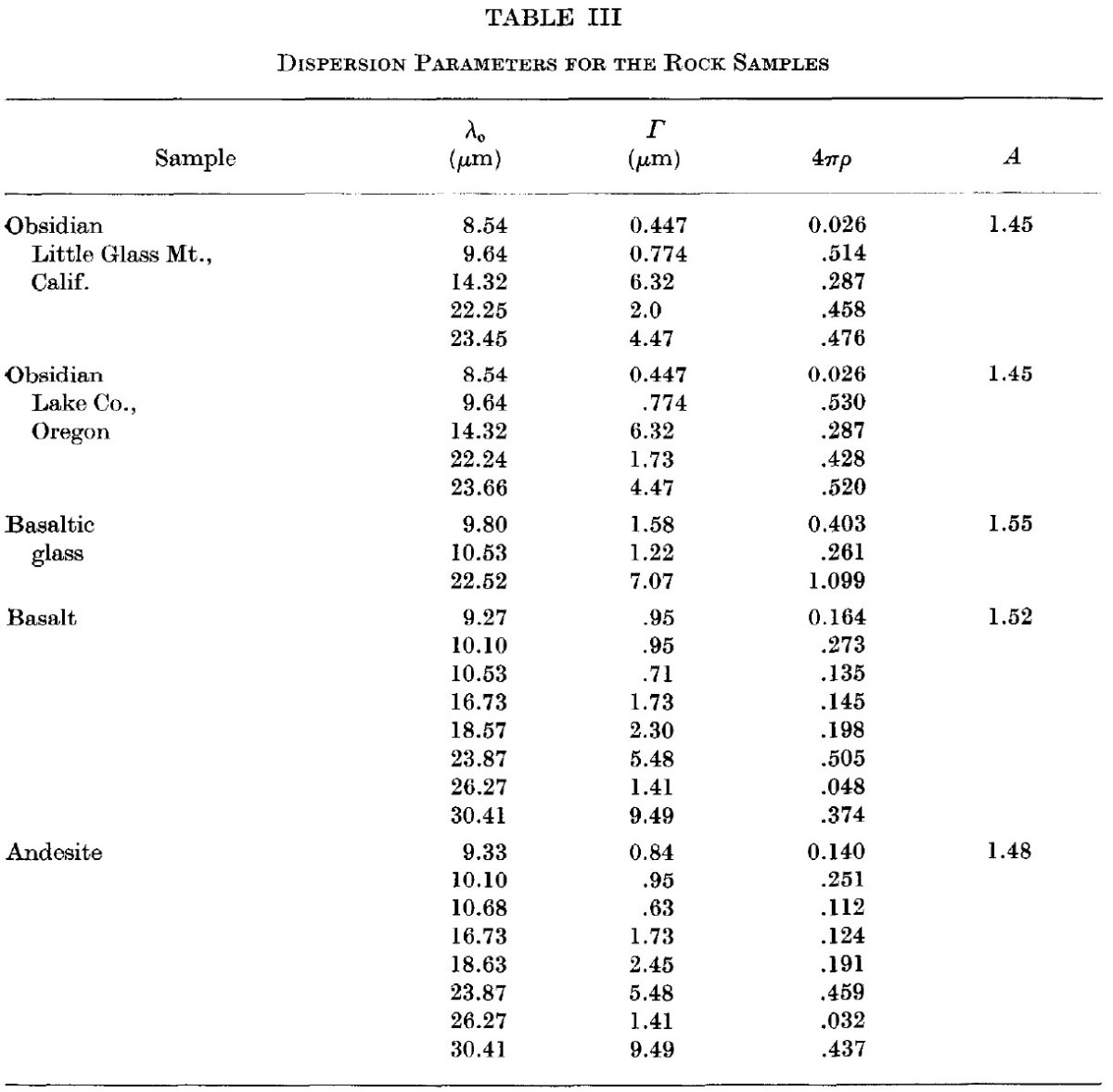
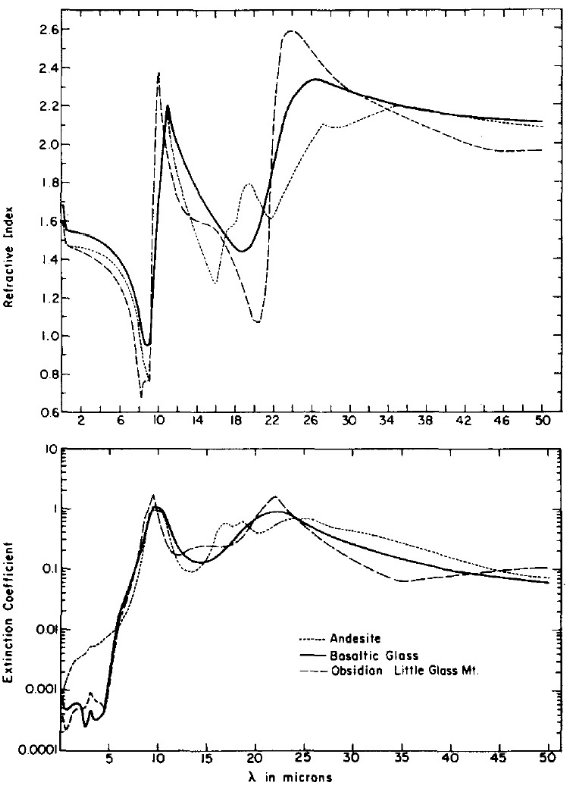図４．黒曜石、玄武ガラス、安山岩の光学定数。 　

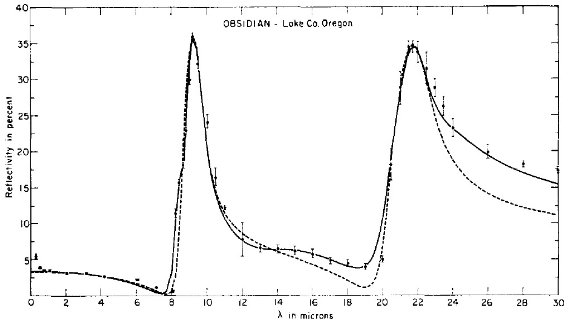図５．黒曜石の破線＝２振動子と実線＝５振動子モデルの比較。黒点＝ 測定反射率。 　

　　


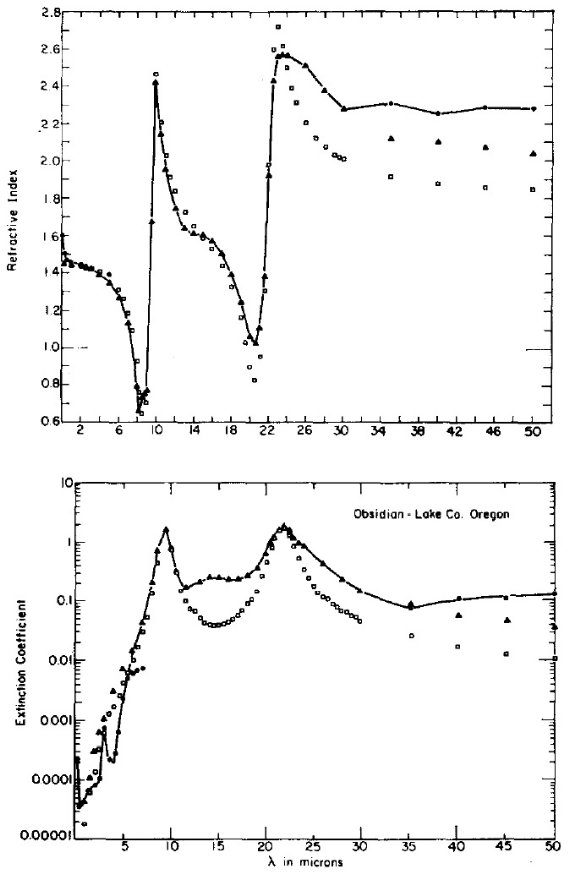図６．黒曜石の光学定数。実線＝最終的な平滑化後の光学定数。黒点＝ 透過曲線と反射曲線からビアーの法則とフレネルの規則を用いて求めた 光学定数。四角＝二振動子分散式によるフィット。三角＝五振動子分散 式によるフィット。5 μm 付近での黒点と三角のズレは図５に示す 6 - 8 μm での分散式のフィット不足が原因である。 　

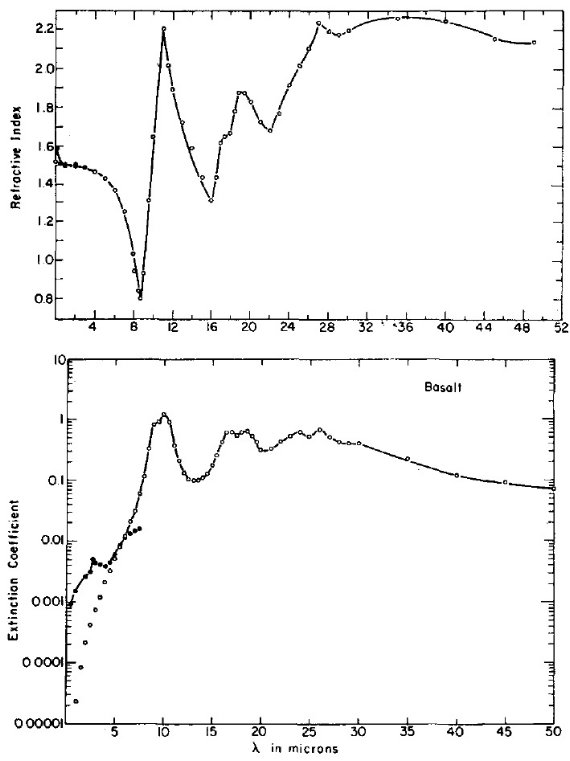図７．玄武岩の光学定数。実線＝最終的な平滑化後の光学定数。黒点＝ 透過曲線と反射曲線からビアーの法則とフレネルの規則を用いて求めた 光学定数。白丸＝振動子分散式によるフィット。三角＝五振動子分散 式によるフィット。 　

　結論　

　 λ < 4 μm 吸収率に差　

　岩石とガラスの光学定数は測定全領域で似通っていた。大きな差が生じるの は λ < 4 μm での吸収係数である。この差は極端な場合２桁に まで達する。吸収率が一桁違う二種類の黒曜石では、反射曲線は殆ど同じで、 屈折率もほんの少ししか違わない。
(非晶質＝ガラスは却って可視・近赤外 の吸収率が下がるというのはまずいな。 )

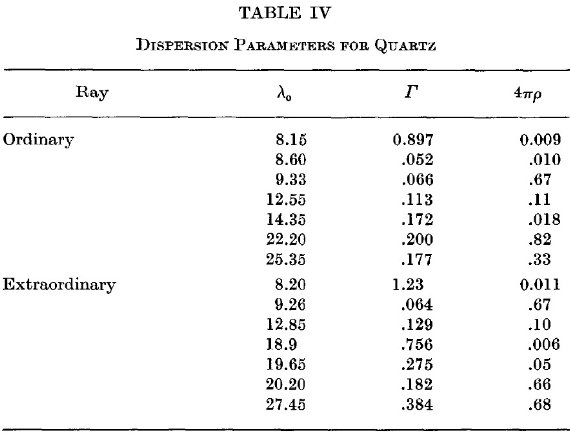表４．コルツの分散パラメタ―