| 全スペクトル型に亘る超巨星の分布と運動を、特にガスとの相関を重点的に、 調べた。この研究に用いた星は表にまとめた。これら超巨星の 60 % はグループ で存在している。オールト定数 A = 14 km/s/kpc が得られた。また二次係数が -0.6 km/s/kpc2 と求まった。 | 星とガスの速度を比較した結果の一致は良かった。これらの超巨星は比較的 ガスの濃い箇所に多い。星の運動残差はグループの運動が非円周回転であること を示唆する。カリーナ・ケンタウルス領域では腕の両側で系統運動 10 km/s が 検出された。これは Lin の密度波理論の予想に合う。ペルセウスの運動残差は 部分的にはこのずれ運動のためかも知れない。 |
1.イントロダクションBidelman 1958, Sharpless 1965 は中間、晩期型の超巨星の分布を調べた。 その後データが増えたので、今回総まとめ。 |
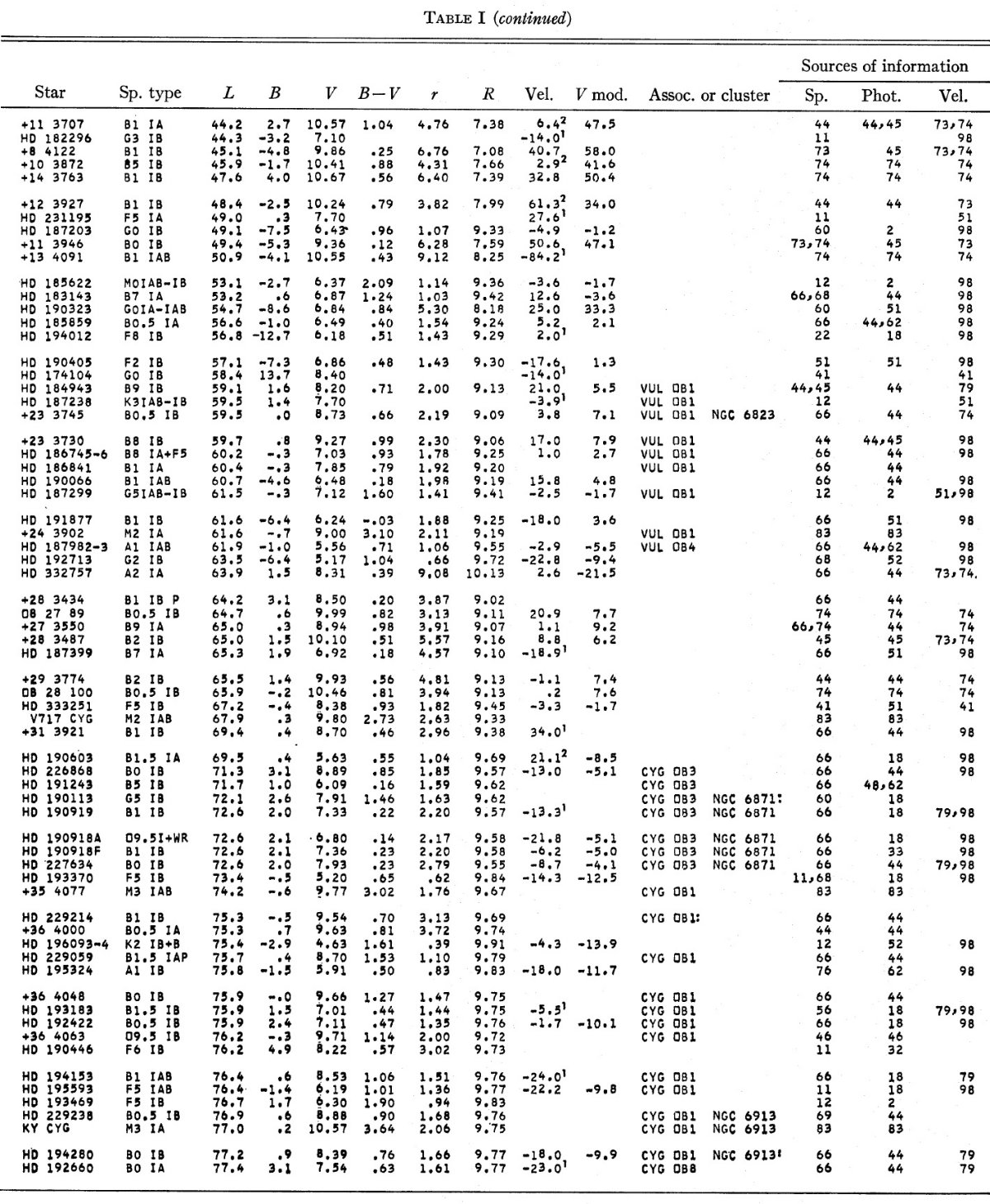
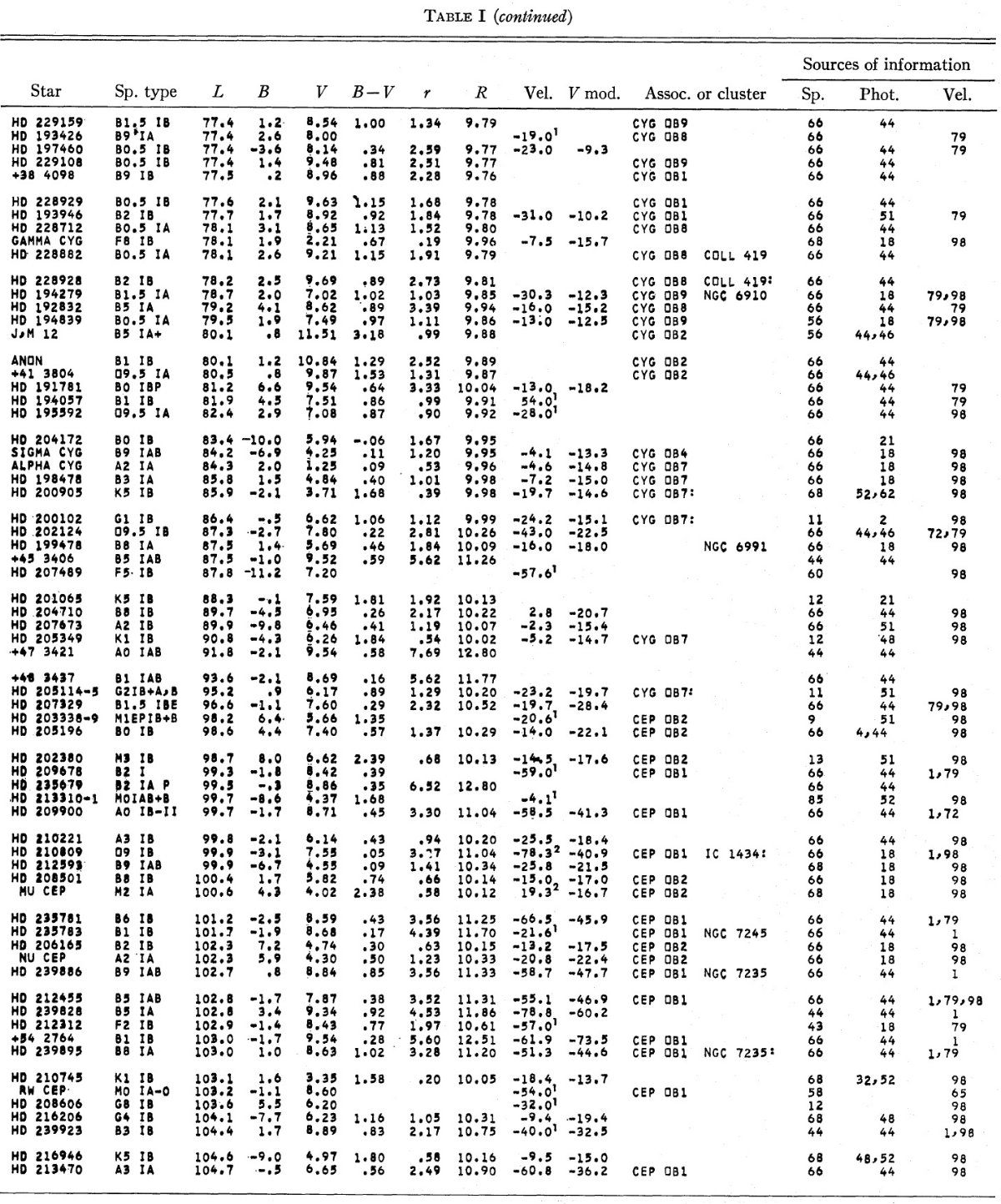
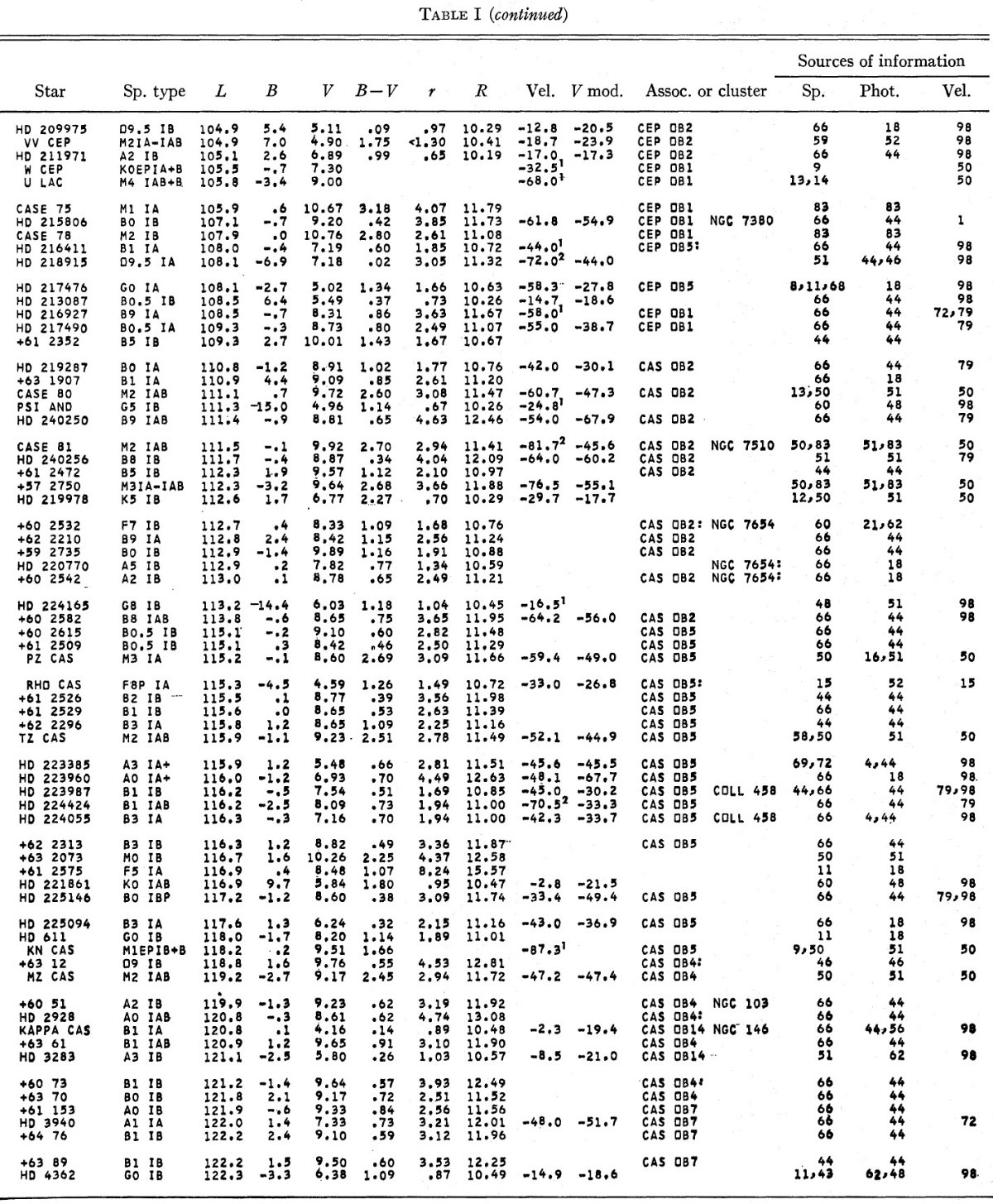
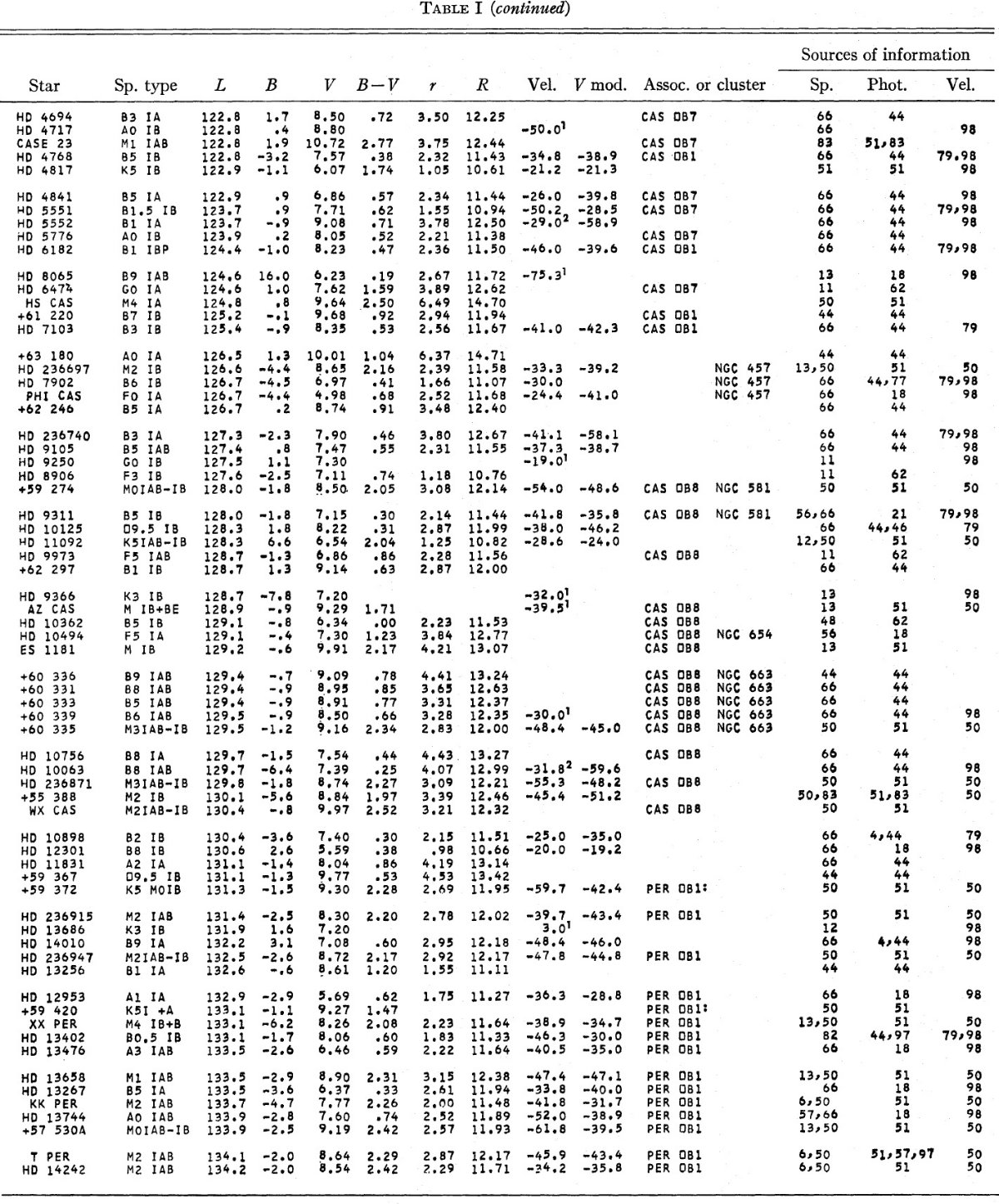
2.カタログBidelman の集めたカードデータに著者のデータを足した。光度クラス Ib か それ以上の巨星 669 星がリスト表1に載った。Blaauw 1963 の光度較正を用い た。Johnson 1966 の固有カラーを用いカラーエクセスから R = 3.0 で星間吸収 を定めた。銀河中心からの距離は Ro = 10 kpc を仮定して求めた。 表1のモデル視線速度はもし星が銀河回転に乗っていたら期待される速度である。 |
|
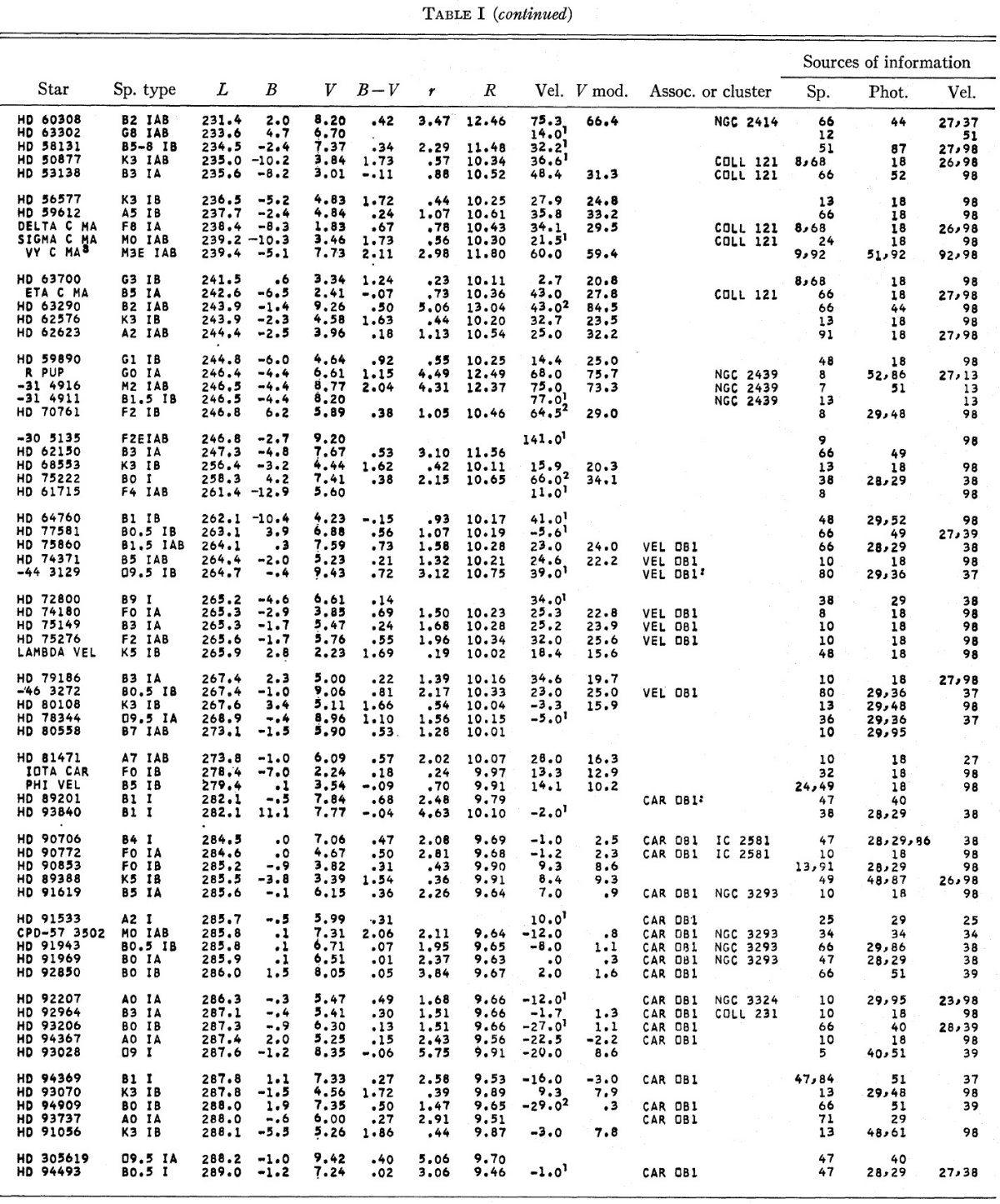
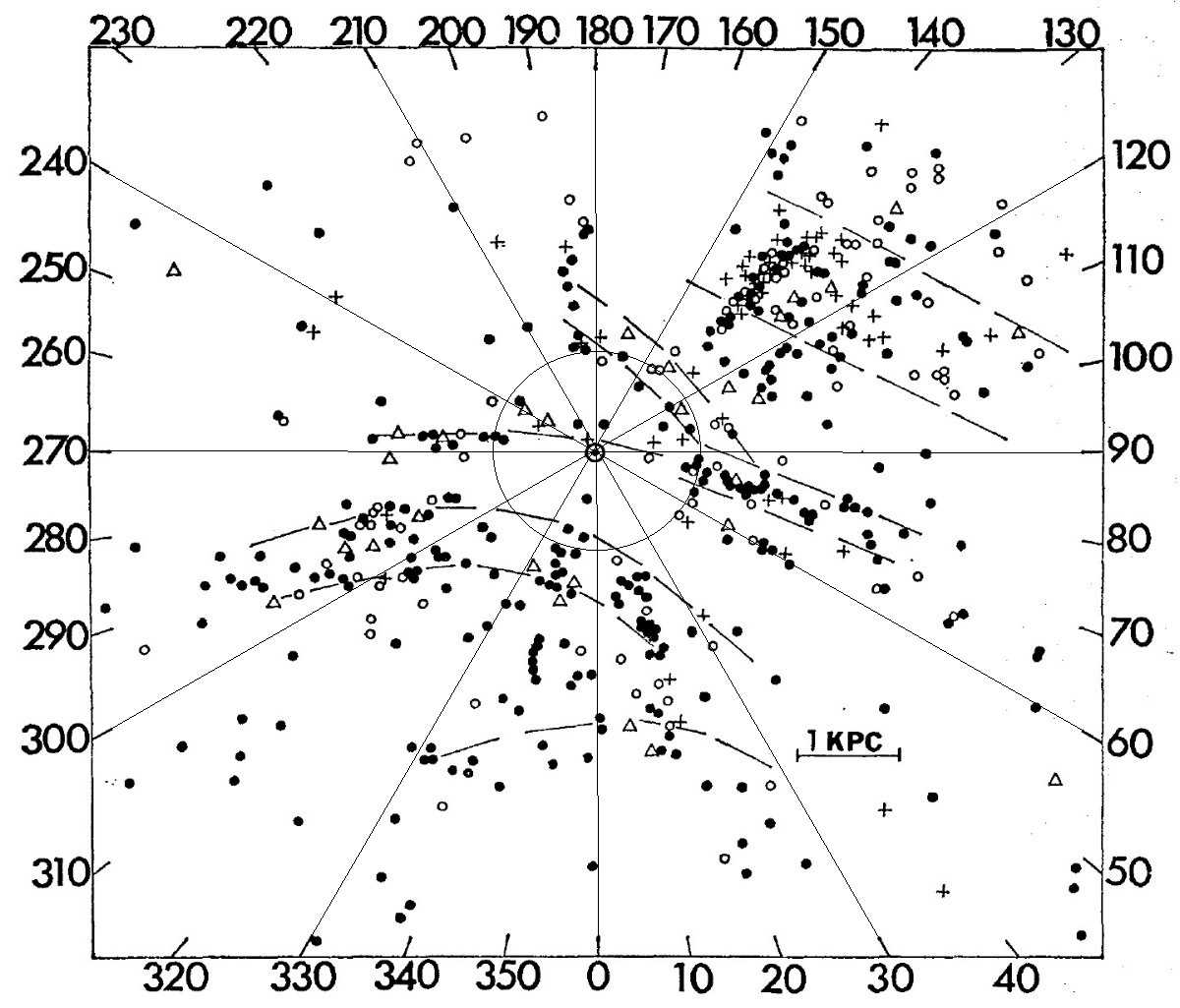
サンプル 図1には、B5 より早期の超巨星全てと、B5 より晩期だが Ib より明るい ものをプロットした。Ib で晩期型を除いたのは年齢が近い星を集めたかった からである。図1の散らばりは個々星の距離指数の不定性約 0.5 等が原因で ある。 渦状腕 それでも、図1を見ると、超巨星が幅広の渦状腕を成していることが判る。 超巨星から期待される腕の形を図に描きこんだ。それらは、 (1)サジタリウス腕。l = 30 - 200 で D = 2 kpc に位置する。 (2)オリオン腕。l = 70 - 270 で太陽近傍を通る。 (3)ペルセウス腕。l = 100 - 140. D = 2 - 3 kpc. サジタリウス腕の向こう側には多数の超巨星が存在する。おそらく、遠方の 腕に付随するものだろう。 図2=星団 散らばりを抑える目的で、星団、アソシエイションに属する超巨星をまとめ、 その平均距離を用いたプロットを図2に示す。超巨星の 60 % は何らかの集団 に属している。これは Morgan (1953) が採用した OB-アソシエイションの分布と同じ手法である。 |
腕の巾 散らばりが減少したため、図2では腕がよりはっきり見える。 腕は依然として幅広だが、これは位置のエラーによるものではない。個々の エラーは 200 pc 程度だが、ペルセウス腕は約 800 pc 巾で、 l = 125 - 135 に天体の集中が見られる。サジタリウス腕の幅は 500 pc で、オリオン腕 は狭くて 300 pc である。 カリーナ腕とオリオン腕はつながらない Bok 1959 はカリーナ腕 l = 285 - 300 がオリオン腕の延長ではないかと 提案した。しかし、l = 20 - 70 と 265 - 285 にある空白域はこの二つが 分離した構造であることを明らかにする。オリオン腕のスパーが反中心方向に 延び、ついにはペルセウス腕に接続する可能性がある。半中心方向は超巨星 に欠ける領域である。 サジタリウス腕の内側腕 図1、図2のどちらにも l = [330, 30] 方向、太陽から 3 kpc に内側腕が ある兆候が見られる。 |

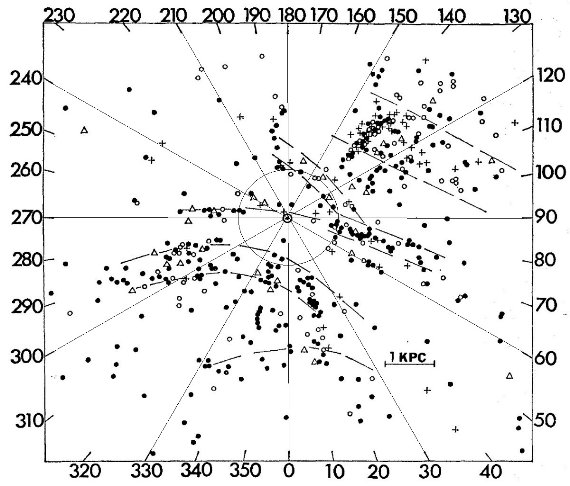 図1.黒丸=O9 - B5. 白丸=B5 - A5. 三角=A5 - K5. 十字= K5 - M. |
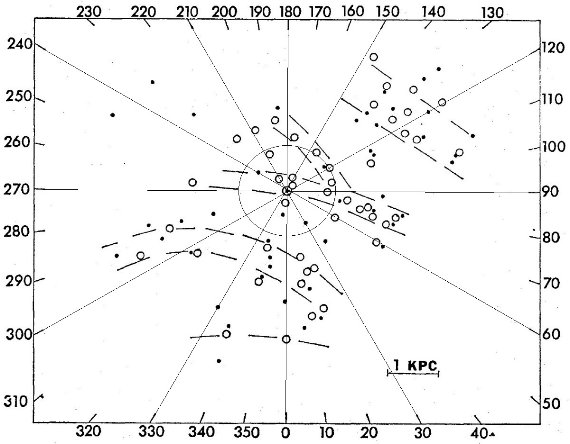 図2.白丸=アソシエイション。黒丸=銀河星団。で超巨星を含むもの。 |
|
微分回転 超巨星の距離は大きいので、微分回転の表現に一次近似は不十分である。
とする。A1 はオールト定数 A である。微分回転 VG は以下のようになる。 VG = -2[A1(R-Ro) + A2(R-Ro) 2]sin(l)cos(b) サンプル星 当初は次の基準で 401 超巨星が選ばれた。 (i)|b| < 10 (ii)距離精度が良い (iii)視線速度が良い(General Catalog of Stellar Radial Velocities) |
最小二乗解 太陽運動と K-項を足した視線速度 V=VG+uocos(l)cos(b)-vosin(l)cos(b) -wosin(b)+K 最小二乗解の結果は表2に示す。 この式の解を求める際に、 Feast, Shuttleworth 1965, Kraft, Schmidt 1963 を参考にして 24 星を除いた。また、太陽を含む集団運動の影響を考慮して、 距離別にグループ分けして解を求めた。 興味深い点 (i) A1 距離の大きなサンプルで決めた A1 は収束する傾向にある。 (ii) A2 幾つかの解から A2 = -0.7 km/s/kpc2 らしい。 これまで、この値についてははっきり決まってこなかった。 (iii) 太陽運動 太陽運動の値は回転定数にはあまり影響しない。 |
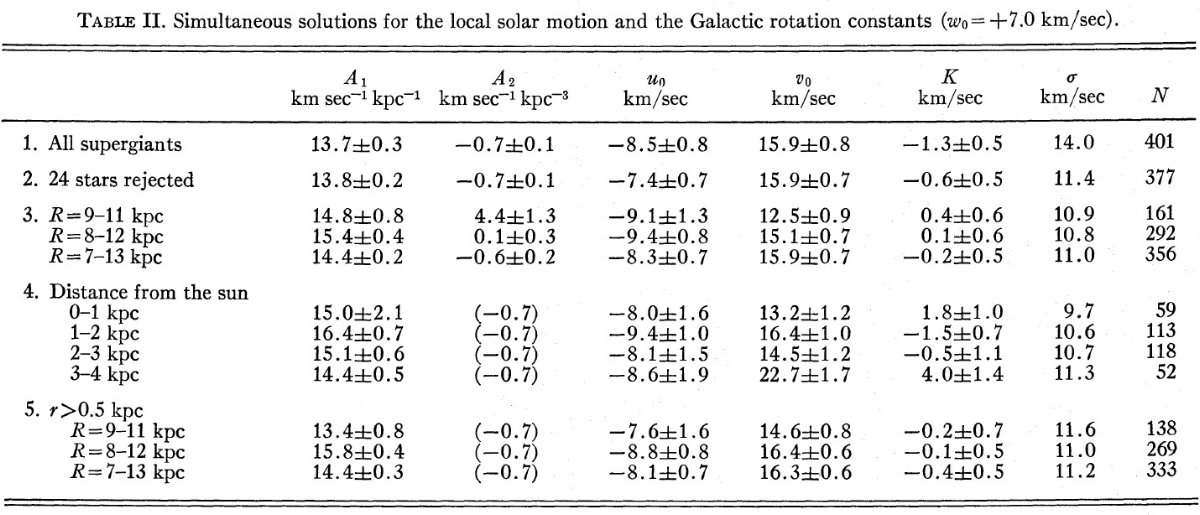
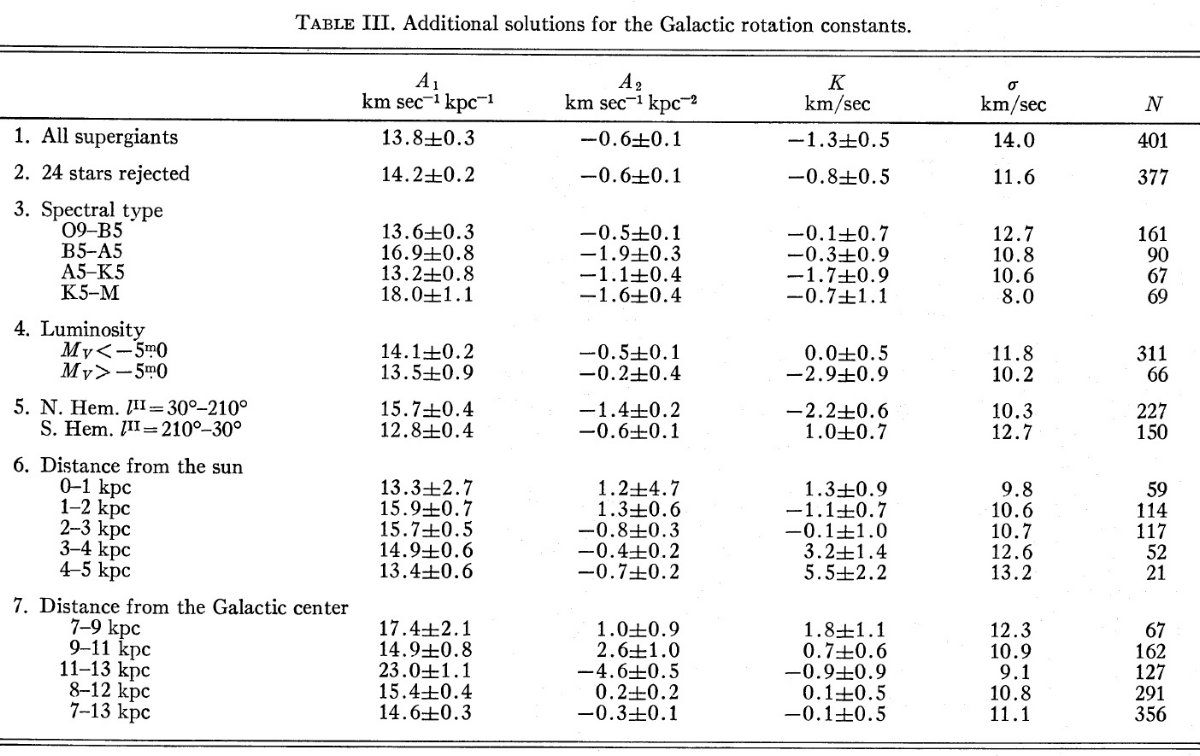

|
シュミットモデルからのズレ 図3に超巨星の角回転速度を示す。点線は 1965 シュミットモデルである。 太陽近く、 R = 8.5 - 11 kpc では、観測点はシュミットモデルと良く合う。 しかし、 R = 11 - 12 kpc では星の観測値はシュミットモデルより下に来る。 これらの星はペルセウス腕に属する。この系統的なずれは星かガス、または双 方が非円周運動を行っているためであろう。 セファイドも同じズレを示す Miller 1968 はペルセウス腕の HIIRs がシュミット回転より下に来ると 述べた。彼は Kraft, Schmidt 1963 のセファイド回転曲線が R = 11 - 12 kpc で同じ現象を示すことを指摘した。超巨星とセファイドの回転曲線は両者が 同じ運動学に従うことを示す。 R > 12 kpc ではセファイドは再びシュミット モデルに載る。このように、超巨星、セファイド、HIIRs の回転曲線はシュミット 回転曲線からの系統的なズレがペルセウス腕で起きることを示す。 |
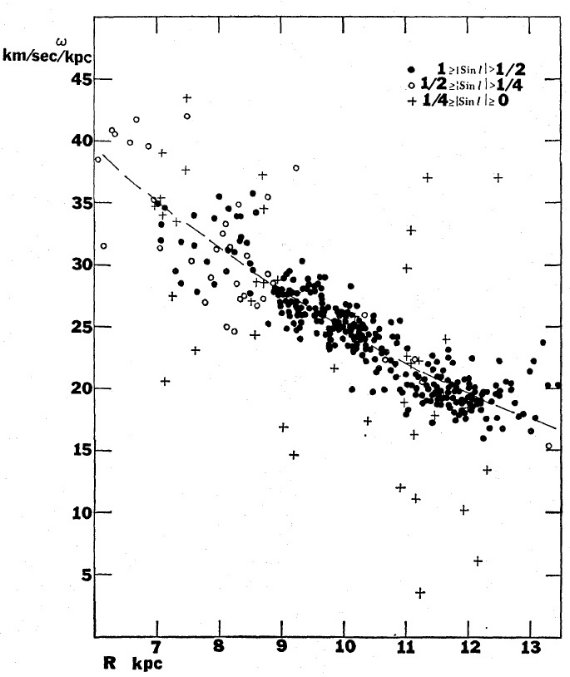 図3.超巨星の角回転速度。点線= 1965 シュミットモデル。 |
|
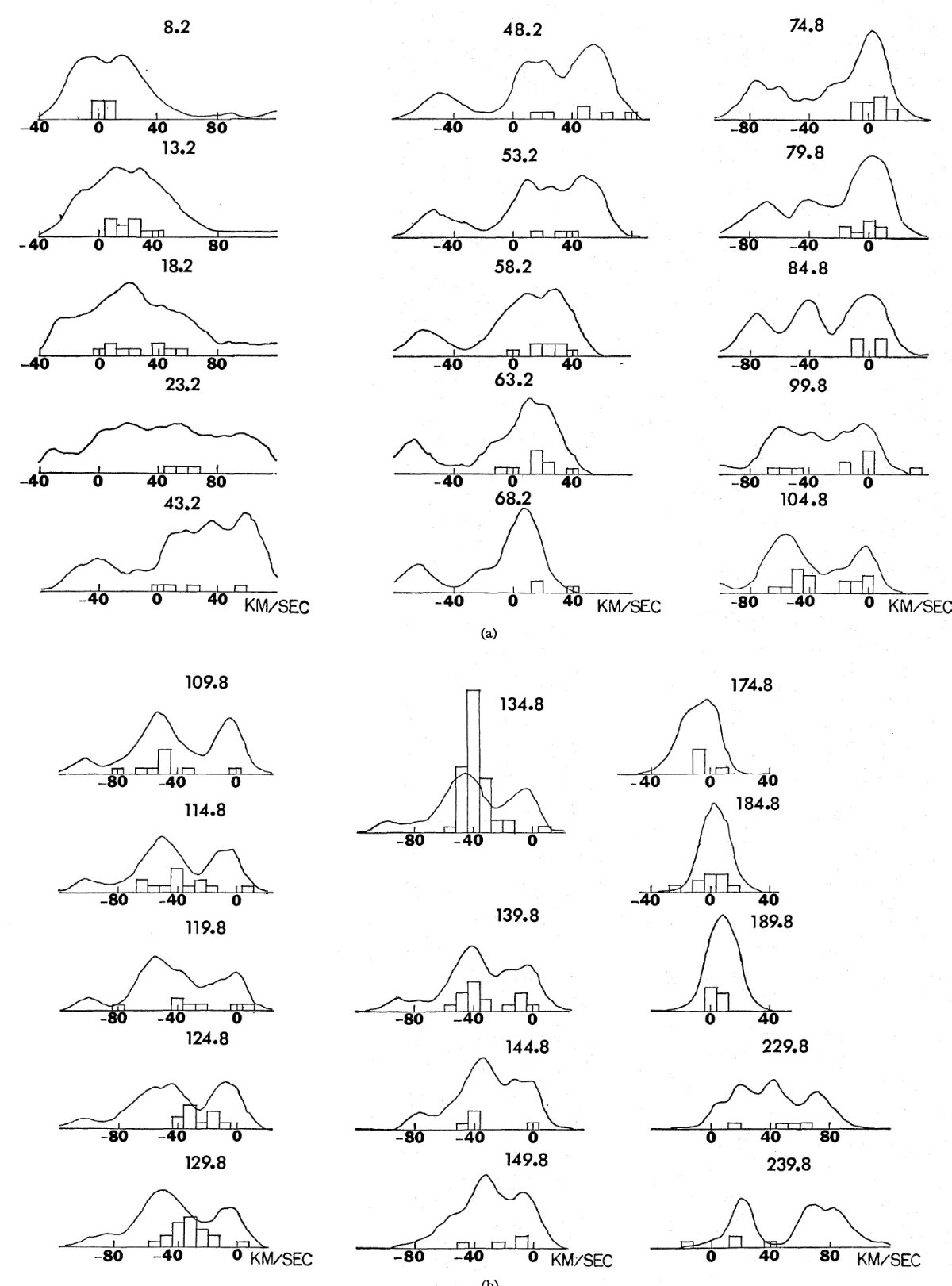
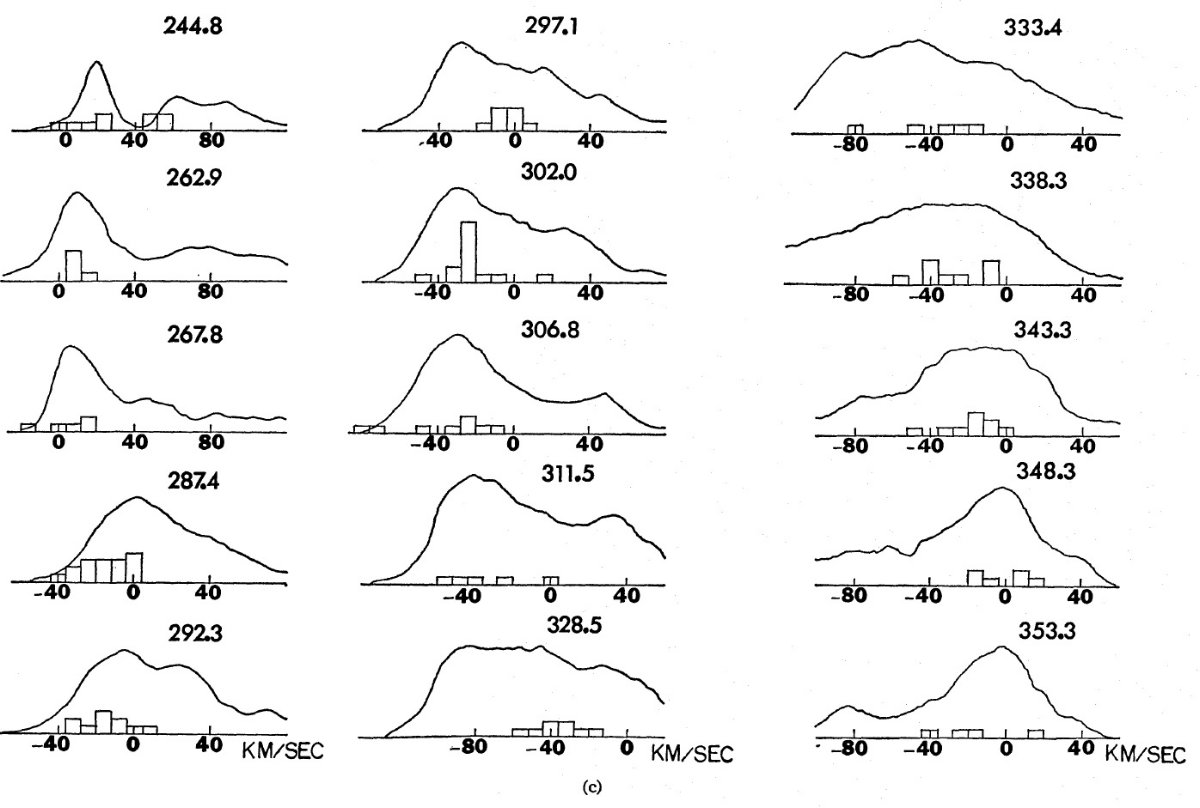
円運動からのズレ HI 21 cm マップはガスの分布を示す。 Fletcher 1963 は運動距離を用いて 種族 I 星の位置をガスのそれに重ね、良い対応を得た。この対応自体は 銀経と視線速度で較べるので、モデルに依らないことが大事である。 Becker 1961 と Sharpless (1965) は若い星の測光距離を用いて、 HI 分布と 比較した。両者には明らかな差があり、それは距離エラーによるかも知れな いし、銀河系モデルのためかも知れない。しかし、 Sharpless (1965) によると、 興味深いことに一致が良かったのは速度が距離に最も鋭敏な4方向であった。 電波の結果との相関には銀経依存性がある。従って、光学距離を全体的に 修正しても不一致は改善されない。銀河系モデルが不一致の原因らしい。 運動学モデルは円運動を仮定している。このため、方向毎に若い星とガスの 両方が円運動からの系統的なズレを示すのであろう。重要なことは、lv-図 では星とガスは一般に一致が良い。 星の速度頻度と HI プロファイルピーク 図4には銀経の小区間毎に超巨星の速度分布を HI ラインプロファイル (Kerr, Westerhout 1965)に重ねて示す。 全体として、星速度の頻度分布は HI ラインプロファイルのピークに対応する。 この対応は銀河系モデルに無関係である。反中心方向では星もガスも小さな 速度巾を有す。 l = 60 - 90 では、星の速度は HI ピークと良く合う。 l > 90 の第2ピークは可視ペルセウス腕に同定され、星速度も同じように 二つに分割されている。 ガス密度と超巨星の対応 表5には、ピーク速度から 16 km/s 以内に5個以上の超巨星を含む、21 cm ピークの平均速度と対応する星平均速度を示す。差は小さく速度分散の範囲で ある。星の速度データは完全でなく、特に遠方ではそうである。更なるデータ 取得が必要である。このデータバイアスを考慮して、図5では個々の星の 速度を水素密度等高線(l-v 図)の上にプロットした。l = 85 - 240 では HI 等高線は Westerhout 1957 に依っている。 l = 240 - 40 は Kerr et al 1959 を使用した。 l = 40 - 85 区間は等高線が与えられていないので、 Schmidt 1957 のラインプリファイルから再建する必要があった。 HI 密度分布を調べると、超巨星は濃いガスに存在するが、最も濃い箇所とは 一致しない。最も濃い領域のサイズは小さく、星の速度分散を考えると、一致 しなくて不思議はない。注意すべきは、若い星を多数含むアソシエイションの 方向を見ると、速度は通常ガスコアの外側に位置する。 |
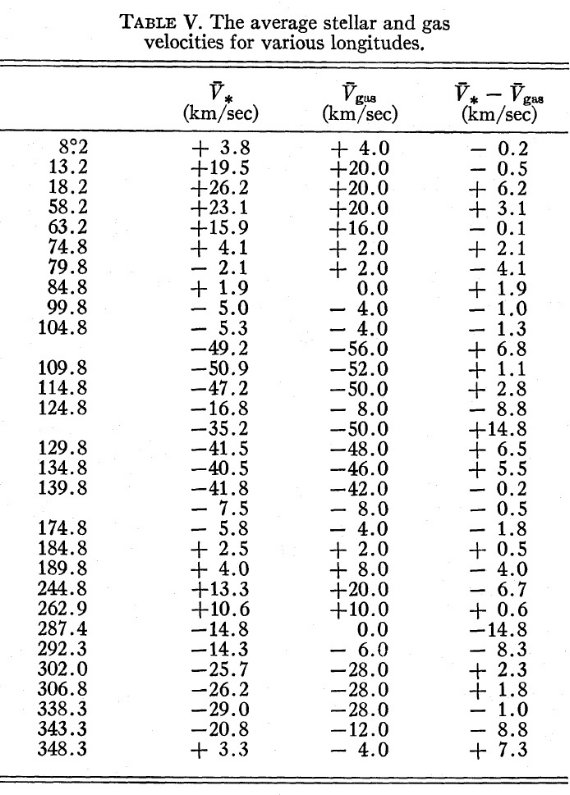 表5.星とガスの平均速度の銀経による変化 |
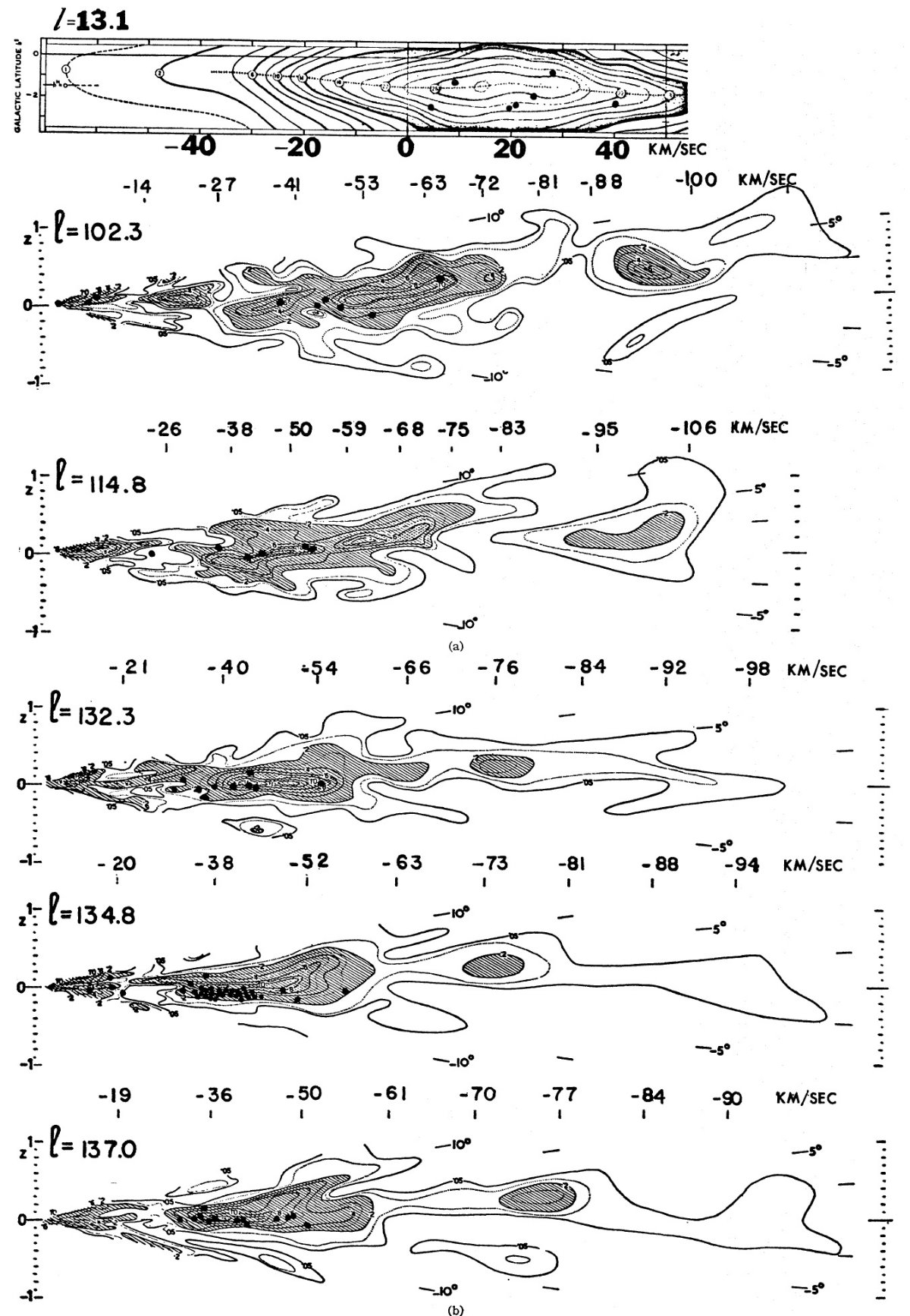
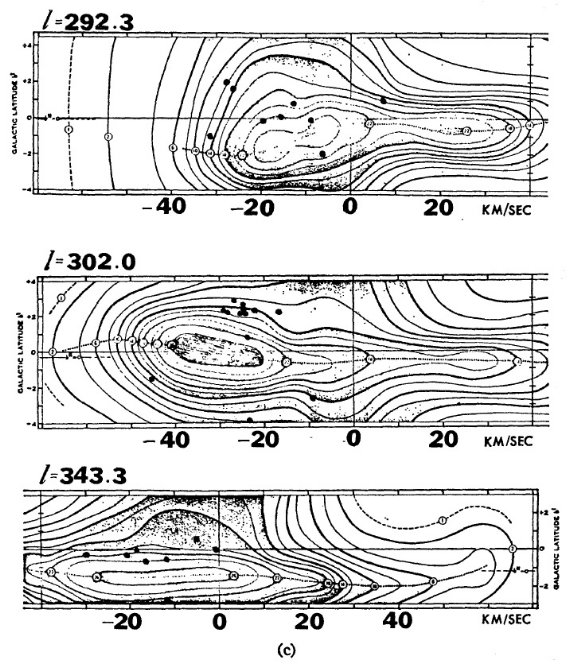
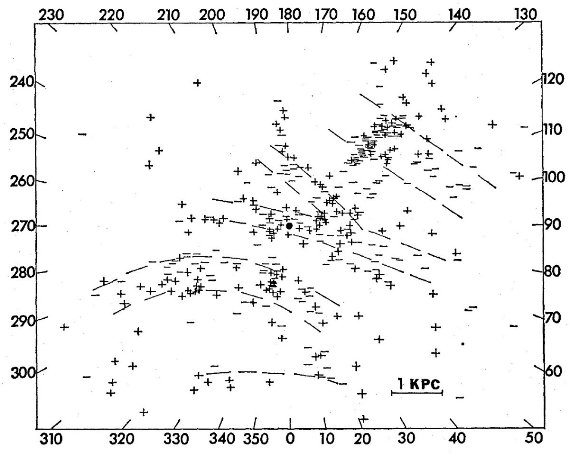 図6.速度残差の符号の分布。 ペルセウス腕は速度残差が負 速度残差 ΔV = Vobs - Vmdl である。 図6には残差の符号の分布を示す。正符号優勢と負符号優勢の領域が分かれて いるのは明らかである。ペルセウス腕では腕全体にわたって速度残差が負で あるという強い特徴がある。興味深いのは l = 125 付近に正の小さな領域が あり、そこは 21 cm が薄い所である。 腕の外側縁で残差が正、内側縁では負 興味深いのは、腕の外側縁では残差が正に、内側縁では負になる傾向である。 腕が角度を持って伸びているため、腕の外側内側の境目の距離は銀経と共に 変わる。図7には双方での残差量の頻度分布を示す。内側縁で負が優勢なことは 明らかである。同じ効果がセファイド (Kraft, Schmidt 1963) でも認められる。 彼らのデータは超巨星と合算されている。その平均値は以下の通り:
内側縁の ΔV は有意であるが、外側縁はデータ数が足りず距離エラーの 影響が大きい。 星団・アソシエイションの残差 距離エラー効果を抑えるには星団・アソシエイションの残差が適している。 表6にはそのデータが示されている。平均残差の結果は、以下の通り:
より多くのデータが必要である。 |
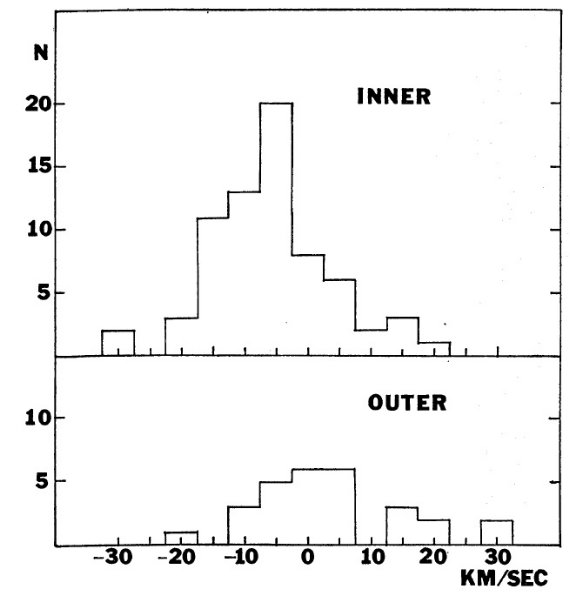 図7.ペルセウス腕の内側と外側における、速度残差頻度の分布。 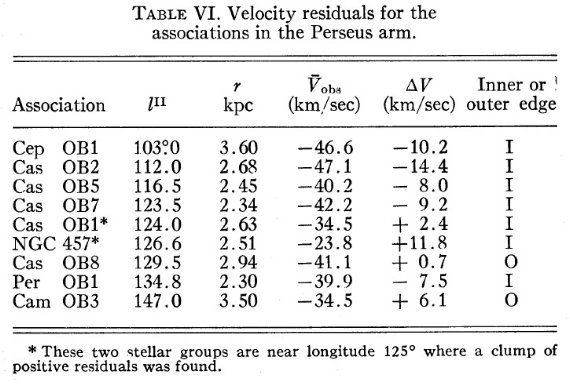 表6.ペルセウス腕アソシエイションの速度残差。 |
|
距離誤差 誤差はあるが、それでパターンは生み出しにくい。それに残差の大きさは 距離エラーに帰するには大き過ぎる。 非円運動(1)=腕の膨張 ペルセウス腕では我々は渦構造を横切る方向に見ているので、腕の膨張運動 をズレ運動と分離するのが難しい。 非円運動(2)=ズレ運動 Miller 1968 はペルセウス腕内の星団、アソシエイション、 HIIRs のプロ ットとそれらの速度残差の考察から、l が大きくなると負の残差が小さくなる (正方向に変わる)ことを見出した。これは、残差が腕に沿ったズレ運動によ ることを示唆する。 |
カリーナ・ケンタウルス領域のズレ運動 l = 285 - 300 のカリーナ・ケンタウルス領域では、腕に沿って見ることに なる。そこでは残差が外側縁で大きく負となり、内側縁で正になる。 この差は明らかに腕の両側でのズレ運動を示す。内側の 18 星平均残差 = 10.0±5.5 km/s, 外側 19 星では -8.2±6.5 km/s である。 この残差はおそらくズレ運動の大きさなのであろう。 密度波モデル Lin et al 1969 の密度波モデルでは銀河回転に対して腕の内側縁で 10 km/s のオーダーの系統運動を予測しているのは興味深い。 |
|
回転定数 超巨星の分布と運動の解析から、オールト定数 A = 14 km/s/kpc という値 が得られた。これは以前の研究と合う。また二次係数として -0.60 km/s/kpc2 を得た。 アソシエイションまたは星団のメンバー 超巨星の 60 % がアソシエイションまたは星団のメンバーであることが判った。 明るく、速度分散が小さいので銀河系の遠方構造の追跡子として好適である。 |
ガスとの相関 少なくとも速度空間では HI と超巨星の相関が良い。超巨星はガスの濃い ところに多いが、 HI 密度のピークと一致するわけではない。 非円運動 速度残差は非円運動を示唆し、それはおそらく HI も共有している。 ペルセウス腕ではそれが K-項、回転曲線、速度残差として現れる。 残差は腕全体で負であり、部分的にはずれ運動のためかも知れない。 カリーナ・ケンタウルス領域では、残差は腕の両側で符号が逆になる。 その大きさは 10 km/s で Lin et al 1969 の密度波モデルと合う。 |