| SMC, LMC, Fornax, Carina, Sculptor dSphs 内の AGBs サンプルからの マスロスを調べた。スピッツアー搭載赤外分光器で測った 225 炭素星と 171 O-リッチ星のスペクトルに可視、赤外測光観測を加え、を輻射輸達モデルで フィットした。そこから光度とマスロス率を出した。現存データの解析から 変光周期を求めた。 | VMC の K-等級、IRAC 4.5 μm 多期観測、ALLWISE+NEOWISE から非常に 深い赤外天体の 1000 日を超す周期を決めることができた。サンプル星全ての マスロス率と光度を決めた。文献に載っているマスロス率は今回の値とかなり 異なることがあるが、それは適用する光学定数の違い(場合によっては数倍の差) とモデル化の手法が主な原因である。 |

2.1.スペクトル表1にここで使用された Spitzer データをまとめた。最後のプロ グラム以外は LMC, SMC に集中してる。スペクトルは主に IRS = Infrared Spectrograph の low resolution module :SL = Short-Low 5.1 - 14.2 μm と LL = Long-Low 14.0 - 37.0 μm で撮られた。分解能は 60 - 100 である。 非常に赤い星の幾つかが high resolution module :SH = Short-high と LH = Long-High でも撮られた。 |
2.2.サンプルを考える研究間でサンプルの分類に食い違いがある天体が幾つかある。 |
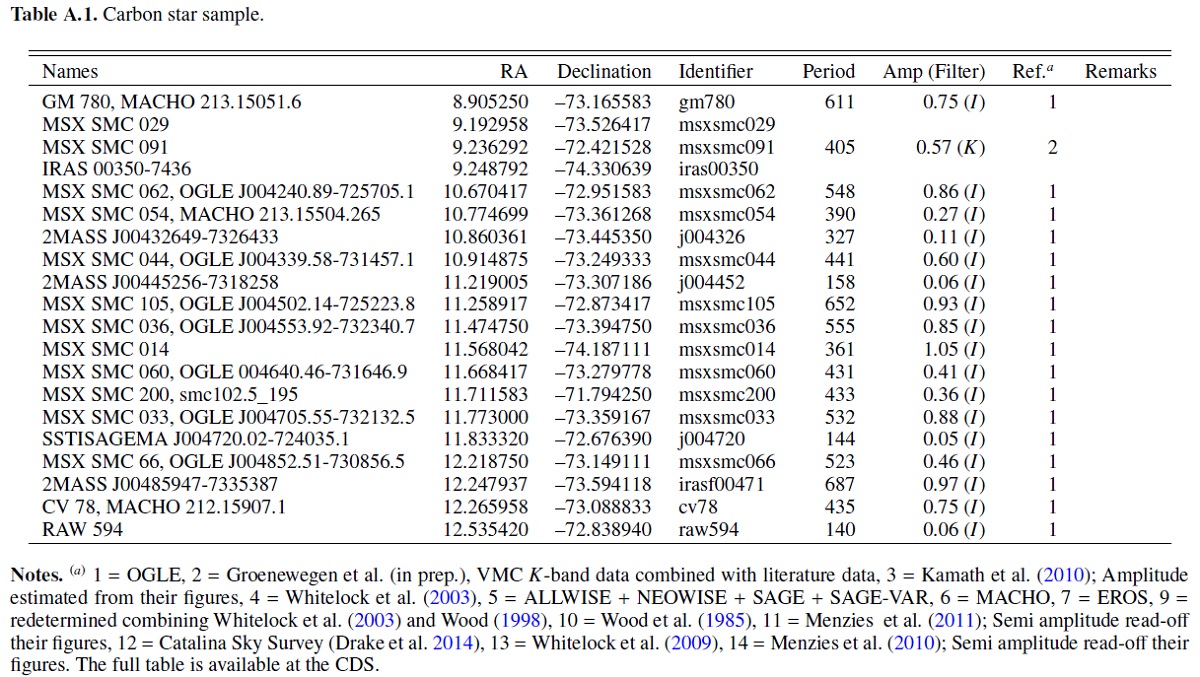
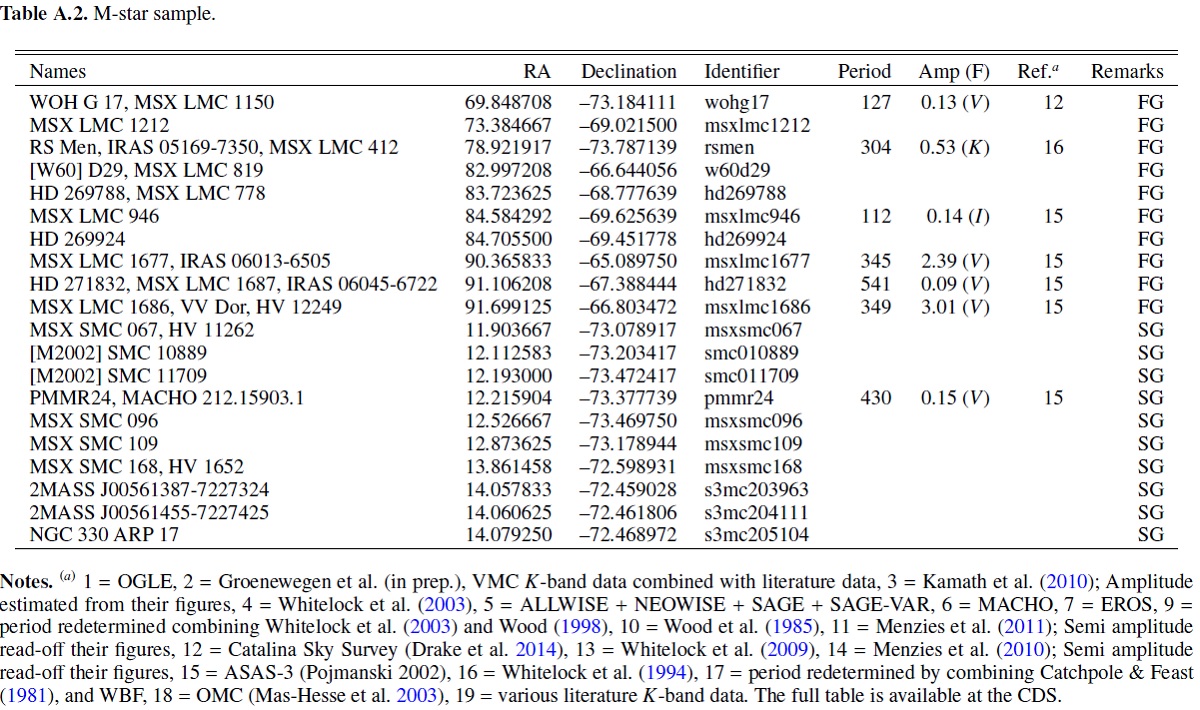
表A1とA2にはサンプル星の一部に対する基本情報を載せた。
完全な表は CDS から得られる。
多くの可視、赤外測光データが文献から得られた。
3.2.周期OGLE, EROS, MACHO は変光の有力な情報源である。可視では CSS = Catalina Sky Survey, INTEGRA 上の OMC = Optical Monitor Camera, ASAS-3 も使った。 赤い星の変光データは赤外で得られる。VMC データは短期間(6-12 ヶ月)精々 15 点くらいしかないが、他にデータがない時は頼った。 |
もっと赤い星には ALLWISE Multiepoch Photometry Table と NEOWISE-R
Single Exposure (L1b) Source Table を用いた。ただし、Sloan et al 2016 に
倣い、数日データの平均をとることは止めた。 SADGE-VAR カタログには、あるなら W2 データも加えた。 サンプルには OGLE に周期が載っている星が 180 星あった。その 85 % (88 %) では我々が OGLE から導いた周期は 5 % (10 %)以内で一致した。6 % の星では 我々が採用した周期は OGLE に第2周期として記載されていた。 Sloan16 は ALLWISE + NEOWISE データを用いて、それまで周期が未定だった 5 つの炭素星の周期を見出した。 |
4.1.輻射輸達コードを走らせる外径DUSTY を一部改良した MoD = "More of Dusty" Groenewegen12 コードを 走らせた。モデルの外径は Td = 20 K で決めた。それは (4-20) x 1000 Rin に対応し、実際に放射光が出る領域よりずっと大きい。 マスク IRS スペクトルで S/N が悪い波長帯や背景放射の 差し引きが上手くいかなかった箇所にはマスクを掛けて最小化操作に加えなかった。 単純なモデル大気には含まれない強い分子吸収帯、例えば CO+c3 による 5.0 - 6.2 μm 帯、C2H2 による 6.6 - 8.5, 13.5 - 14.9 μm 帯 (Matsuura06)、も外した。 大気モデル 炭素星の大気モデルは Aringer09 から、M-星は MARCS モデル (Gustafsson08) を使用した。 4.2.ダスト炭素星ダスト炭素星ダストは AMC = 非晶質炭素、SiC, MgS の混合とした。 グレインサイズは a = 0.15 μm を仮定した。MgS は 30 μm 帯の説明に 導入されたが、必要量が存在比を上回るという問題があった。層状ダストとい う解決案が提示されている。 |
AMC と SiC は distribution of hollow shpere モデルで計算される。中空
比率 f = 0 - fmax の間に分布させるモデルで fmax = 0.70 が良くフィットする。
M-星ダスト 非晶質シリケイト MgFeSiO4, 非晶質アルミナ AlOx, 金属鉄 Fe, 結晶フォーステライト Mg1.9Fe0.1SiO4 のダストを考えた。 4.3.ベストフィットMoD コードは、光度、ダスト層の光学的深さ、内径温度、密度分布の指数、 を、χ2 最小条件で合わせる。光度は全ての星で合わせられる。 他のパラメターが合わせられたのか、固定値とされたかは表 B 1, 2 に記載さ れている。過剰フィットを避けるため、BIC = ベイズ情報基準を計算した。 ベストフィットモデルは BIC 最小の条件で決めた。パラメターのいくつかは外来で、離散値しか取れない。例えば モデル大気 は 100 K 間隔でしか提供されていない。さらにグレイン吸収と散乱は離散値の 半径と組成で事前に計算された値を使う必要がある。例えば炭素星では、 AMC, SiC, MgS の比率 100 : x : y において x と y は 5 の倍数である。 MoD は離散値の有効温度を持つ大気で動かされ、最良の大気が決まり、次に グレイン半径と組成を変えて最良のダストモデルを探す。こうして ベストフィットモデルへ辿り着くのである。 |
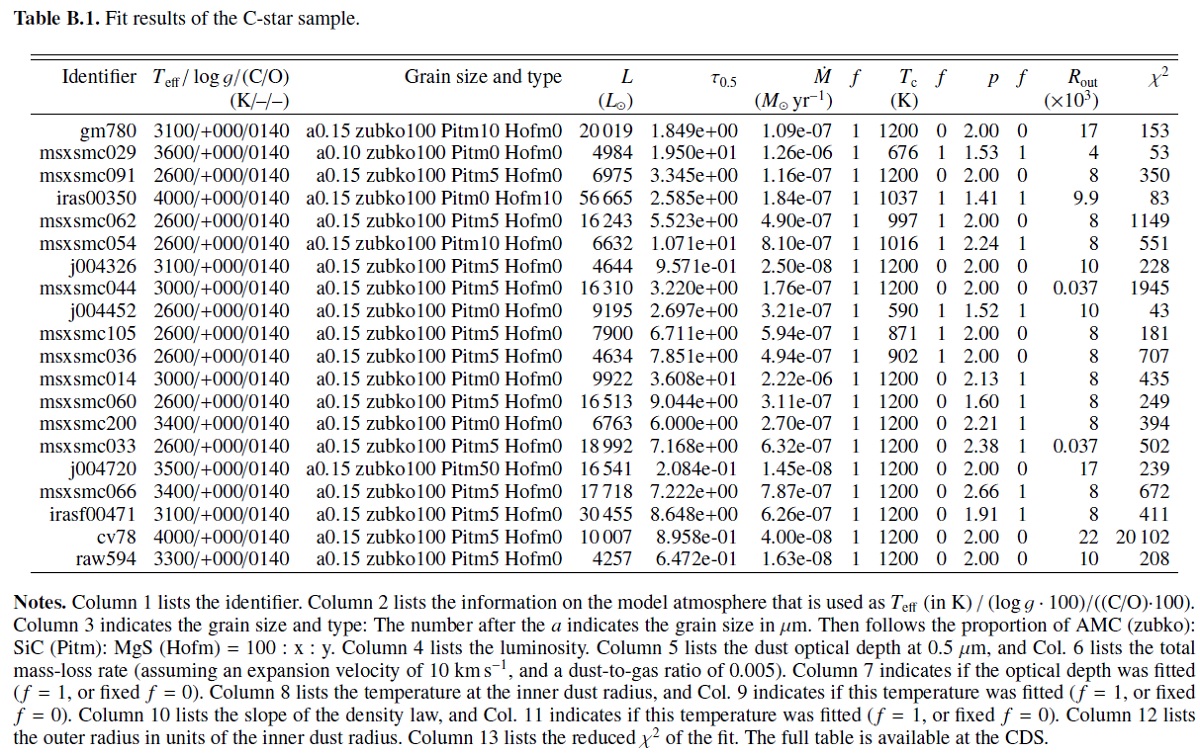
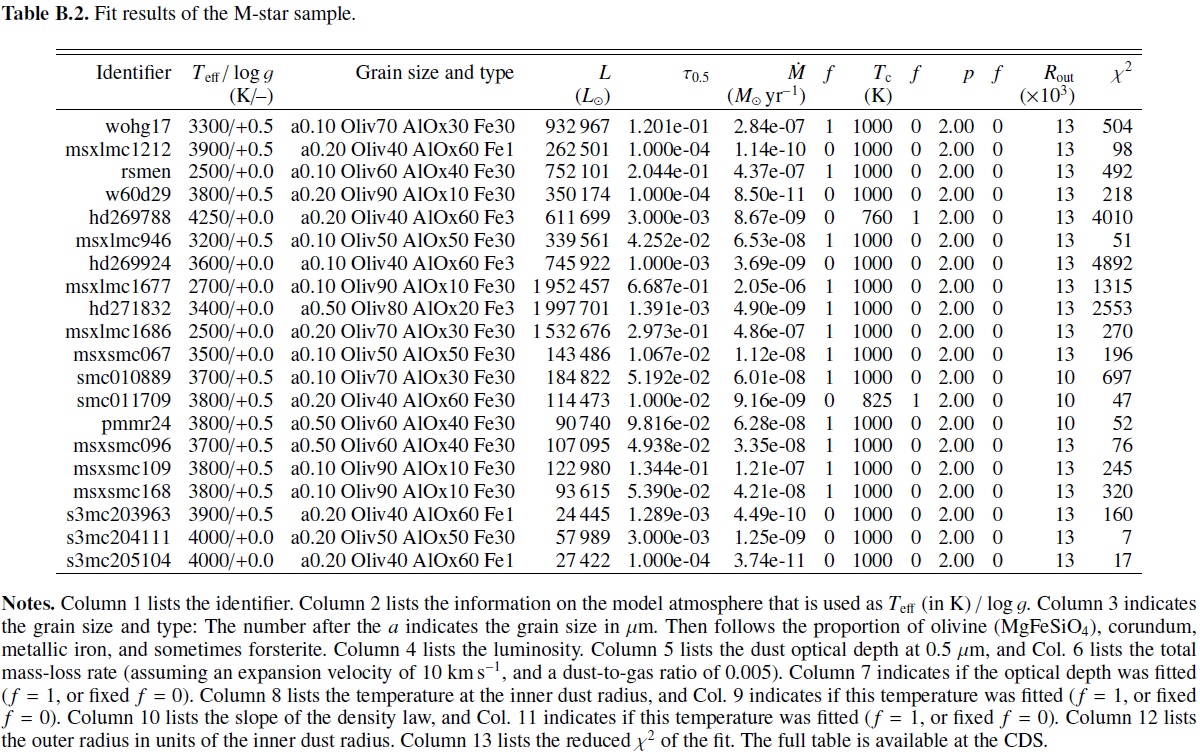
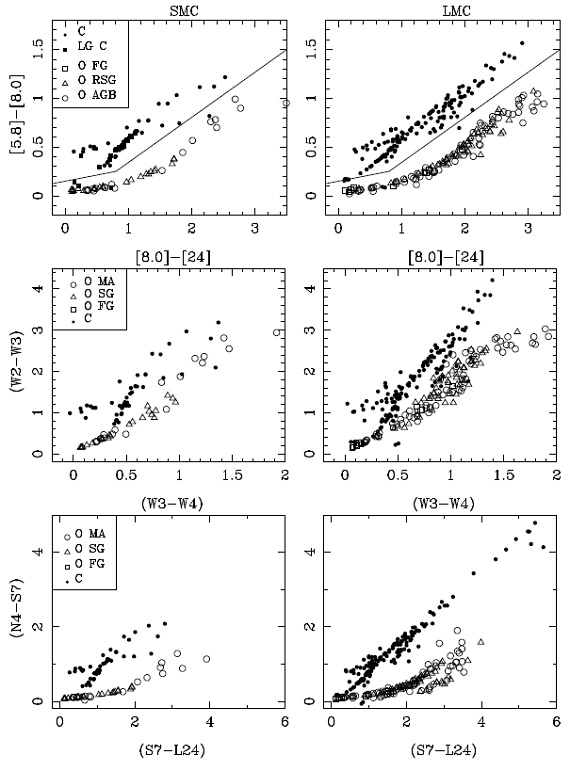 図1.左:SMC, 右: LMC の二色図。上段=スピッツアーカラー。 実線は C-, O-リッチの境界。 中段=WISE カラー。下段=AKARI カラー。 |
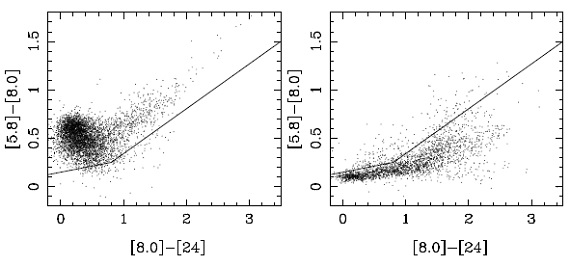 図2.LMC の 左=C-リッチ、右=O-リッチ星のスピッツアー二色図。 Riebel12 による。 表B1 とB2 にフィットの結果を示す。星風速度 10 km/s, ガス/ダスト=200 を仮定したマスロス率も付けた。 5.1.カラー関係C/M 分離図1はベストフィットモデルに対する人工二色図である。Kastner08, Groenewegen09 が示すようにスピッツアー二色図は M-星と C-星の分離が良い。 類似のカラーを使った WISE, AKARI の二色図も示す。分離能は少し劣る。 C-星の 95 % がスピッツアー二色図分離線の上にある。しかし、 10 C-星が M-星域にある。 (なぜ観測カラーを使わない? ) 越境 C-リッチ星 迷い星の2星は特に赤く、 LMC 星は [8.0-24] = 1.9, SMC 星の方は 2.3 である。赤い SMC 星 IRAS 00350 は Sloan14 により C-リッチp−AGB星 とされた。赤い LMC 星は MSX LMC 663 であり、奇妙な SED を示し、 C-リッチサンプル中最も Teff が高い。他の C-リッチ越境星は比較的青く、 ダストなしである。 図2=越境テスト 境界線がどのくらい確かかテストするため、Riebel12 が分類した星を 図2で境界線と比べた。4867 C−星中 161 = 3.3 % が越境した。また 2496 O−リッチ星中 163 = 11 % が越境した。 |
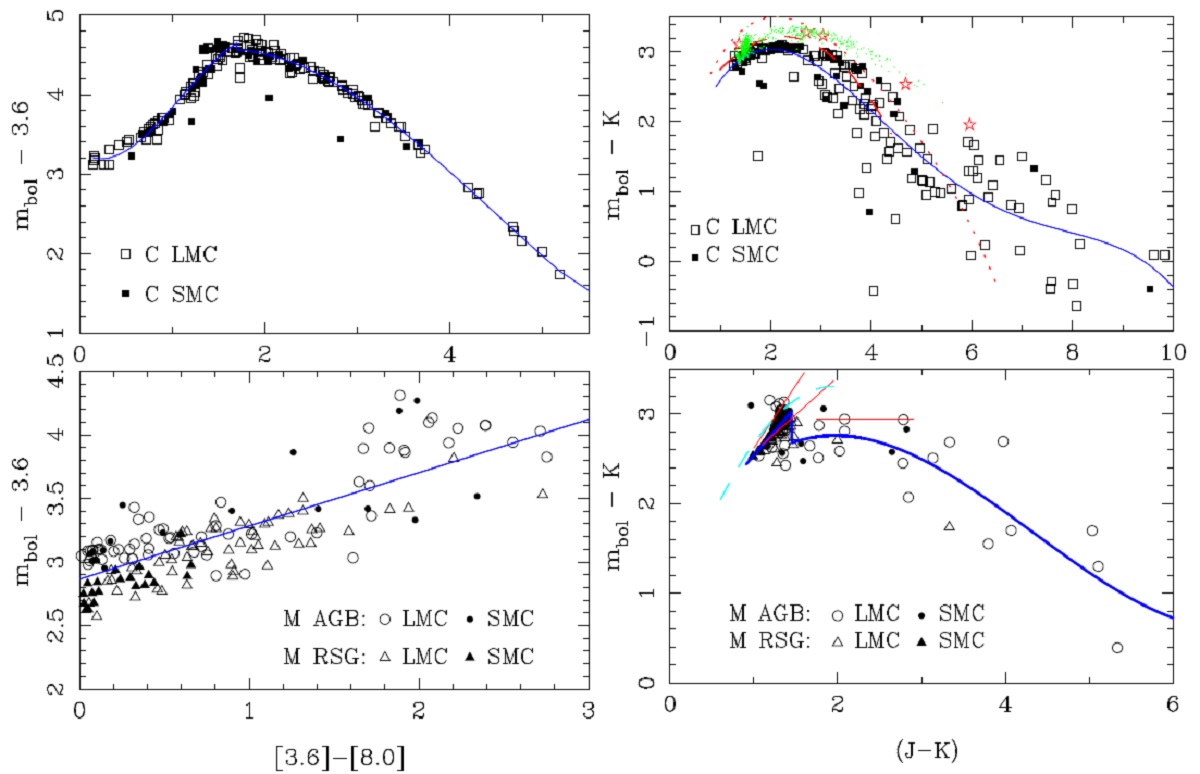
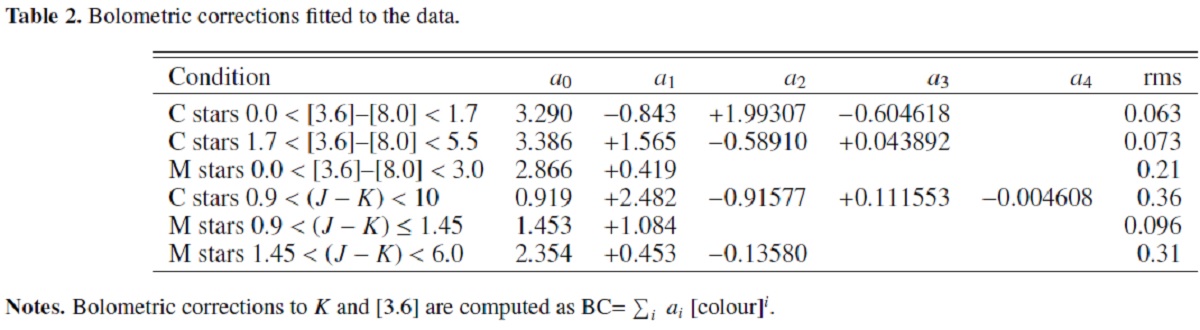
5.2.輻射補正炭素星図3には BC M-星 データが二分されるので J-K = 1.45 でフィットが折れる。 5.3.マスロス率図4=マスロス率図4に、フィットしたモデルに対する、マスロス率とモデルカラーの関係 を示す。関係はタイトで、メタル量効果は認められない。ただし、マスロス率 の導出には星風速度=一定= 10 km/s, ガス/ダスト=一定=200を仮定して いる。 近似式 炭素星は log MLR = -4.080 - 6.531/([3.6-8.0] + 0.941) M-星は log MLR = -4.708 - 2.488/([3.6-8.0] + 0.545) で近似される。 |
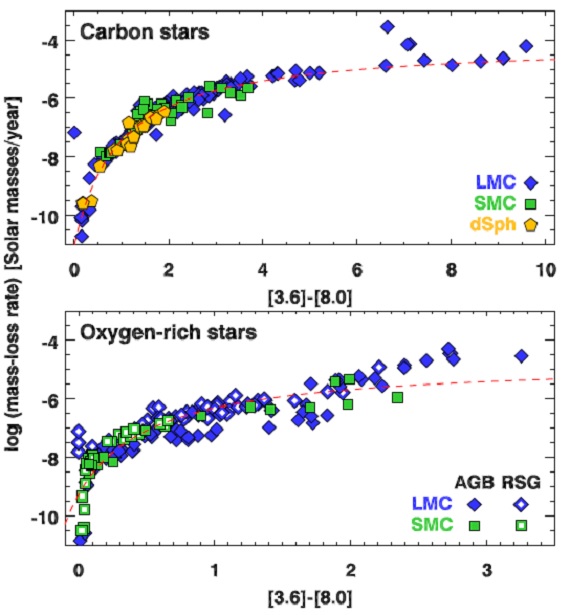 図4.マスロス率とカラーの関係。上:炭素星。下:M-星。 |
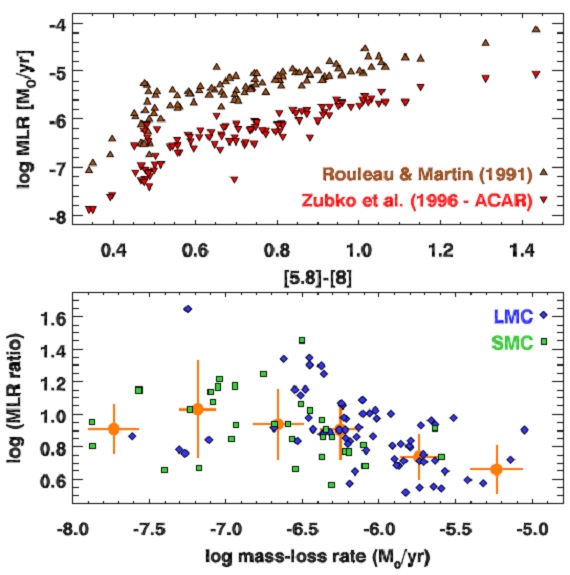 図5.炭素星マスロス率を今回と Groenewegen09 とで比較。今回の光学定数は Zubko et al. (1996) 使用。 G09 は Rouleau,Martin (1991) 使用。 上:両者直接比較。今回のマスロス率はずっと低い。 下:マスロス率の比は大体9。黄金点はメディアン。 6.1.1.Groenewegen09解析面での主な違いまず G09 と今回を較べる。勿論測光データ数、モデル大気、計算コードに 違いがある。非晶質炭素の光学定数が変わり、天文シリケイトの光学定数から 実験室光学定数に変更された。 マスロス率の比 マスロス率の比は、共通する 76 M-星に対し, メディアンで G09/G18 = 1.17 で殆どフィットエラーの範囲であった。 炭素星の変化は劇的である。 101 星での メディアンは G09/G18 = 7.58 である。 その原因は主に Zubko et al. (1996) の ACAR 光学定数の採用にある。 他の例として、Boyer12 と Matsuura13 の LMC/SMC でのAGB 総ダスト形成量が 挙げられる。彼らの推定値は LMC で Matsuura13/Boyer12 = 8、SMC で 11 で あった。Matsuura13 は G09 と同じ Rouleau, Martin (1991) の光学定数をつかい、 同じモデルコードを用いた。Boyer12 は Srinivasan11 の GRAMS モデルを使用 したが、これは Zubko et al. (1996) の ACAR 光学定数を用いている。 どの光学定数を使うべきかにまだ定説はない。 |
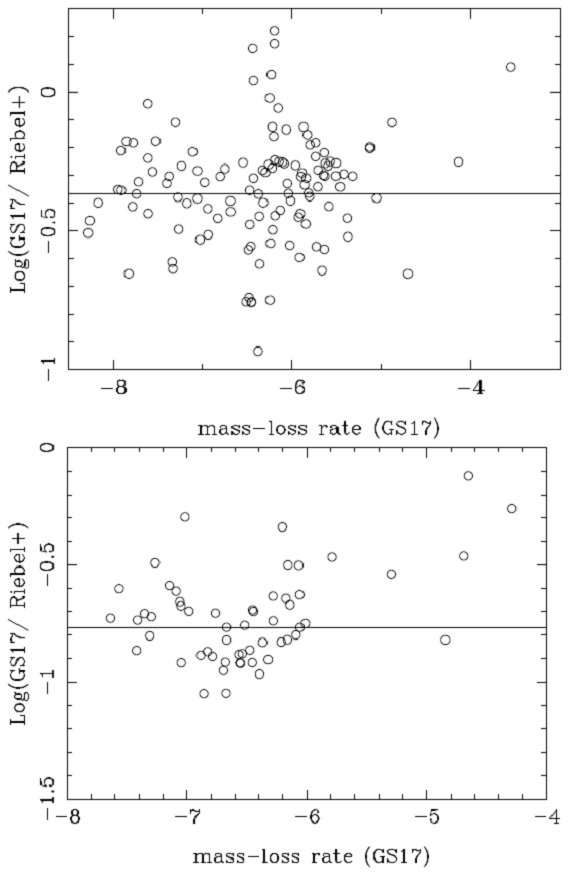 図6.ダストマスロス率を今回と Riebel12 とで比較。 上:炭素星。メディアン=0.46. 下:M-星。メディアン=0.17 6.1.2.Riebel12マスロス率の比Riebel12 は LMC 30,000 AGBs と RSGs を 12 測光バンドでの等級で GRAMS モデルによりフィットして、マスロス率を求めた。図6に彼らと我々の共通星に 対して、マスロス率の比をプロットした。炭素星でのメディアンは R12/G18 = 0.46 であった。 違いの原因 この差は炭素星の場合、主に内側半径の違いによる。M-星の場合、彼らが 天文シリケイトを使い、我々が実験値を使ったことが主因である。 |
6.1.3.Srinivasan11違いの原因Srinivasan11 は彼らの結果を G09 と較べ、かれらのマスロス率は 1.7 倍 低いことを見出した。かれらは Zubko et al. (1996) 光学定数を用いており、それが違い の原因と考えた。しかし、6.1.1.で述べた通り我々の場合その比は 5 - 10 倍となるから、他の原因、例えば使用モデル、も寄与しているに違いない。 表3には GRAMS モデルを較正するための二つの炭素星と二つの M-星を示す。 そこには様々な方法で導かれたマスロス率が比較されている。 注意しておくと、Srinivasan11, 16, Sargent11, Riebel12 は同じ GRAMS モデルグリッドを使用している。したがって、彼らの光度、マスロス率は似て いる。 Jones12 だけはなぜかちょっと違うが。 光学定数以外の要因 光学定数のみではマスロス率の違いを説明するには不十分である。GRAMS モデルは、より高い内側半径温度を許容する。このモデルでは、内側半径を 一定値、炭素星では Rin = 1.5, 3, 4.5, 7, 12 Rs, M-星では Rin = 3, 7, 11, 15 Rs, に固定し, その中で Td が 1800 K (炭素星)、1400 K(M-星) 以下 のモデルのみを採用している。一方、我々のモデルでは 1200 K を超すモデル は排除される。 表3の検討 表3の炭素星 TRM 88 の場合、我々は Rin = 15.6 Rs とした。しかし、 Srinivasan11 はグリッドから 12 Rs を採った。この半径の違いは我々と彼ら のマスロス率比 0.42 に良く合う。もう一つの炭素星 OGLE051306 の場合、 我々は Rin = 14.1 Rs, Srinivasan10 は Rin = 4.4 Rs である。これは 我々の Tin = 970 K, 彼らが 1300 K という違いに繋がる。 |
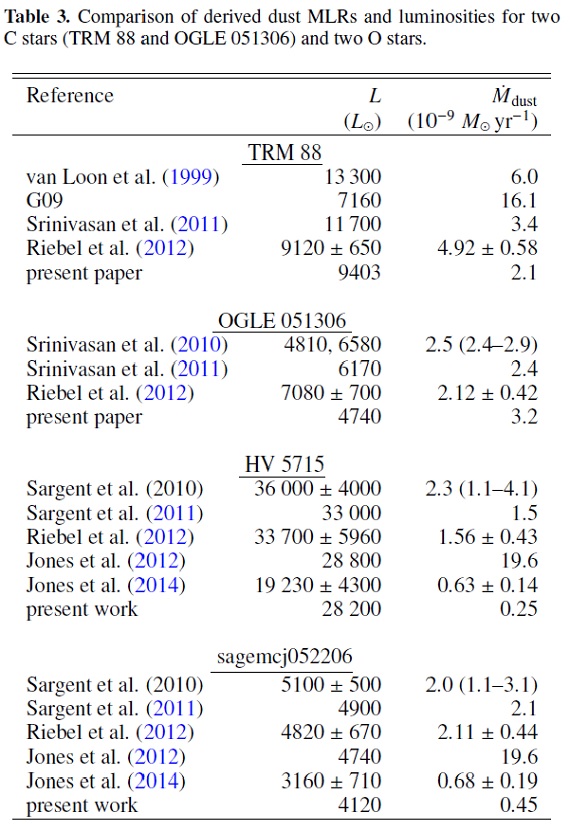 表3.二つの C-星と二つの O-星のマスロス率の比較 |
6.1.4.Jones12Jones12 も GRAMS モデルを使用しているが Riebel12 とは結果が異なる。 共通 69 M 星でマスロス率の比を較べると、メディアンは 1.6 で大きな差が ない。しかし、そのファクター 3 以内に収まるのは僅か 35 % である。 19/69 星はファクター 10以上だし、5/69 ではファクター 75 の違いがある。 |
6.1.5.Jones14Jones et al. (2014) では MODUST コード (Bouwman00) を使用して LMC の星を扱った。 彼らは Jones12 より更に低いマスロス率を得た。その差の違いは主に 使用したオパシティによる。Jones12 では天文シリケイトを Jones et al. (2014) では実験室データが用いられた。我々の得たマスロス率と Jones et al. (2014) の値との違いは小さく一様である。 |
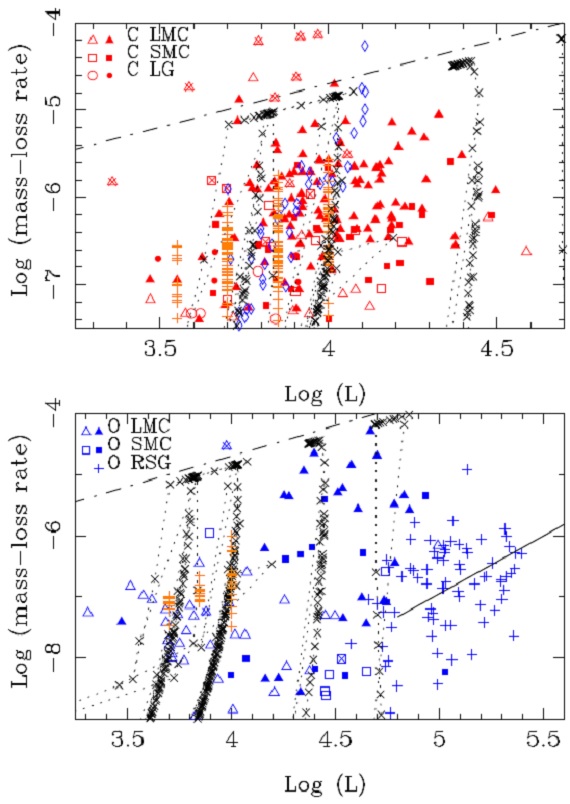 図7.光度とマスロス率の関係。上:炭素星。下:M-星。濃印=ミラ。 白印=低振幅。x=変光情報なし。上図の橙十字=Eriksson14の モデル。上手の青菱形=銀河系炭素星ミラ。下図十字=RSGs。 下図橙十字=BLadh15 モデル。点線=Vassiliadi, Wood モデル 一点鎖線=sngle scattering limit. 実線=MW RSGs の関係(Verhoelst09). |
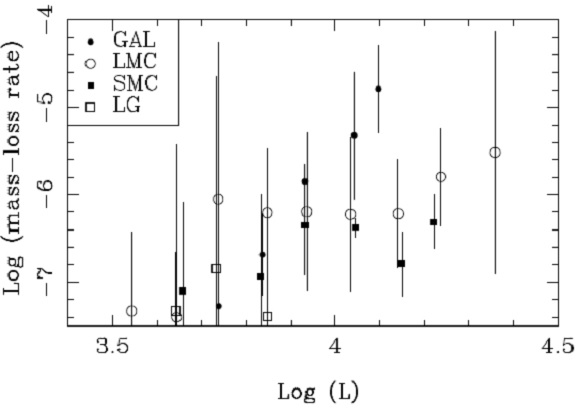 図8.図7の結果を分分けして表現。 進化モデルとの比較 G9 は Vassiliadis, Wood (1993) の恒星進化モデルから予想されるマスロス率-光度関係を Wagenhuber, Groenewegen98 の η=5 AGB 進化モデルと比べた。比較は 大体の所 Vassiliadis, Wood (1993) の方が良さそうであった。このモデルでは、マスロスは single scattering limit の最小値 dM/dt = 2.02 10-8 L/Vesc で与えられる。 炭素星質量帯 図7には、マスロス率と光度の関係をプロットした。モデルは 5000 年おきに プロットしてある。モデルは Mi = 1.5, 2.0, 5.0, 7.9 Mo である。下図 M-星 の分布は G09 で述べられたものと似る。M-星の光度分布は低質量星に対応する 低光度で高い。中間光度では炭素星となるために分布が低下する。それより 高い光度では HHB 効果のため再び M-星が現れる。 |
6.3.スーパー AGB 星MSX SMC 055 = IRAS 00483-7374G09 は MSX SMC 055 = IRAS 00483-7374 がスーパー AGB の良い候補である と述べた。Mbol = -8.0 と高光度であるが P = 1749 days、I で peak to peak 1.6 mag の大きな振幅の変光を示すからである。この脈動はこの星が RSG で ないことを示す。 P−M Groenewegen, Jurkovic 2017 は Bono00 の Mi = 5 - 11 Mo セファイドモデル に基づき、P-L-M-Te=Z 関係を求めた。P=1810, L=85350, T=2500, Z=0.004 というパラメターに対してこの関係式は M = 8.5 Mo を与える。 もっと簡単な Wood90 の P-M-R 関係は基本振動に対し 9.2 Moを与える。 6.4.JWST のポテンシャルKraemer17 は 5.6, 7.7, 21 μm フィルターが C/M 分離に適しており、 5.6, 10, 21 μm フィルターは YSOs と PNe の分離に向いていると述べた。 Jones17a も同様の研究を行った。App. C では 75 フィルターによる合成 等級を示した。そこには NIRCAM, MIRI 装置の 29 バンドが含まれる。 |
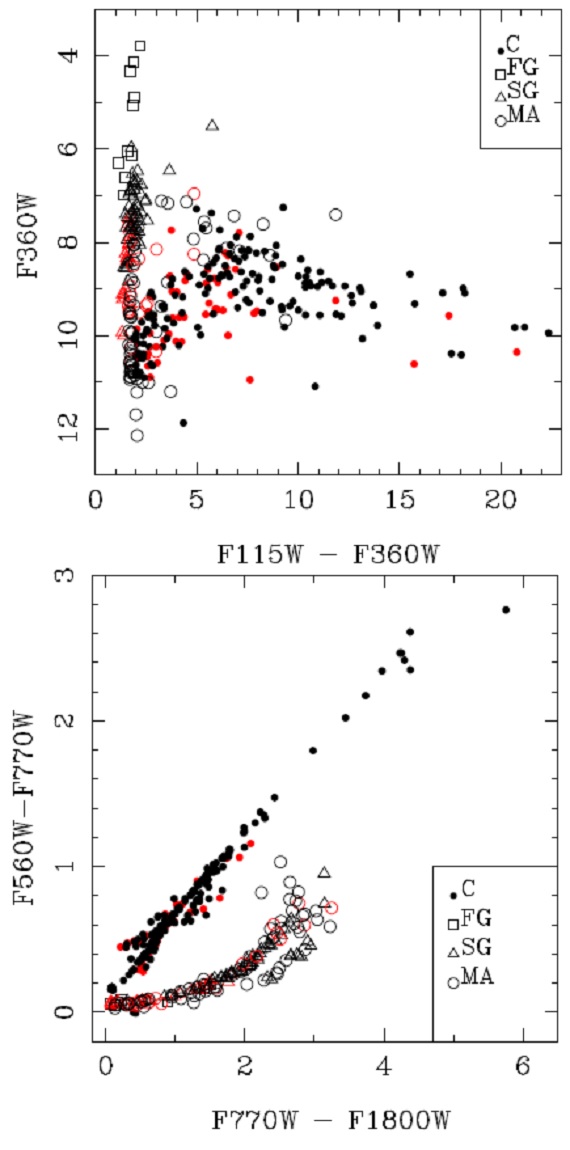 図9.JWST モデル等級による LMC/SMC の CMD と TCD |
|
光学定数と内側半径 LMC/SMC の進化した400 星に SED フィットを行い、光度とマスロス率を 決定した。マスロス率はダストオパシティに強く依存する。 シリケイトの場合、実験室光学定数は低いマスロス率を与える。広く使われる GRAMS モデルでは天体シリケイト光学定数が採用されている。炭素星では 二つの候補のどちらを採用するかで、マスロス率はファクター 5 かそれ以上 変わる。内側半径の許容巾もやはり大きな影響を持つ。 |
非常に厚いシェルの星 光学的深さが非常に大きな星が数個ある。それらは最も明るい星ではない。 Groenewegen16 と Sloan16 はそれらの進化段階を研究した。Marigo13 の進化 コード COLIBRI のモデル結果は Ventura16 と一致し、これらの星が Mi = 2 - 3 Mo で、現在の外層質量は 1 Mo 以下である。彼らの長い 1000 日以上 の周期を説明する為には外層質量が低い必要がある。非常に赤い星の全てが 変光観測が完全に行われているわけではない。 |
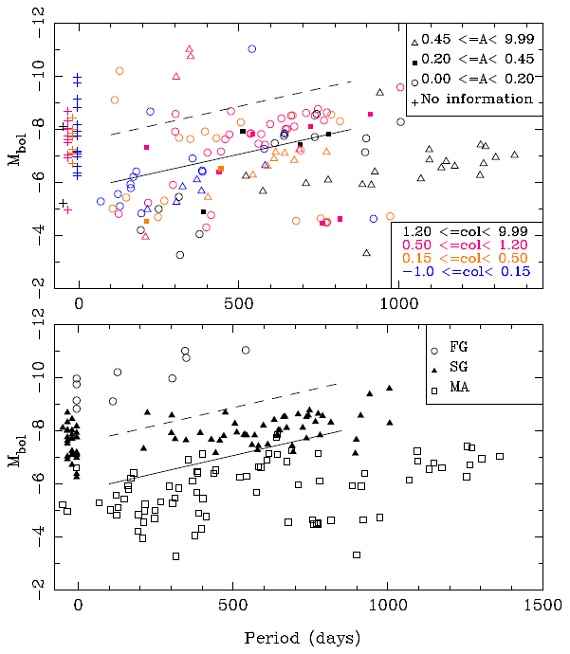
図A1.Mbol - L 関係。上:半振幅で分類してある。 下:前景星や RSGs |
|
|
|

|
|
|

|
|
|
