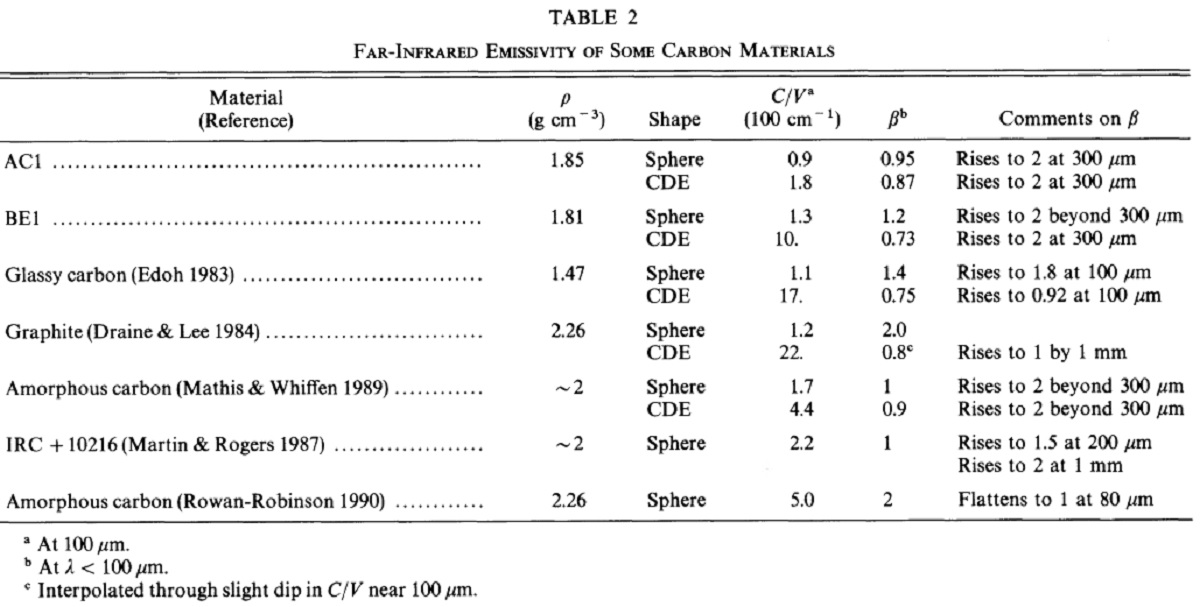
2.1. Kramers-Kronig 法
K-K 関係一般に複素関数 A=Ar - i Ai が E→∞ で A=0 の時、 K-K 関係が成立する。
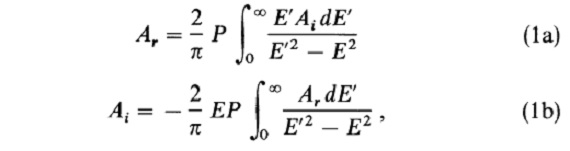
ここに P はコーシーの主値である。A の例としては ε -1 や m-1 が あげられる。ε = εr-iεi は複素誘電関数、m = n -ik は複素屈折率である。
有用な関数は分極率で以下に定義される。
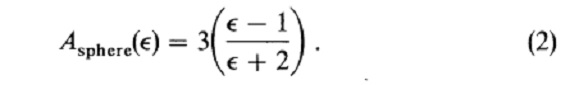
CDE = continuous distribution of randamly oriented ellipsoid
| 非晶質炭素の光学定数を E = 4.1 10-3 - 3.5 103 eV の範囲で求めた。計算に用いたデータは FIR の減光と高エネルギー帯での 他の光学定数測定結果である。光学定数はクラマース・クロニッヒ関係を満たす。 | グレイン形状と集合体効果が光学定数に及ぼす効果を調べ、それが大きいこ とが分かった。CDE 形状分布は定性的に粒子集団効果を表現する。水素化や 非晶質炭素の結合状態が光学定数にどう影響するかを調べた。 |
|
ピュアな非晶質炭素 ピュアな非晶質炭素は sp2 と sp3 結合の網目として 表現される。結合の比率、それに秩序構造の特性長が光学特性に影響する。 Beeman84. ガラス質炭素とグラファイトやダイアモンドと較べれば、特徴依存 性が大きいことが分かる。非晶質炭素の特性は形成条件で変化する。ススの 場合、サイズや形状の分布、集合体効果が測定される吸収、散乱の性質に大きく 影響する。 |
不純物効果 水素が含まれると、少量でも吸収率は、特に可視、赤外域で、大きく低下す る。その際、減光曲線はあまり変わらない。一方、僅かな酸化は赤外域に大きな 変化を及ぼす。それは CH 測定法 赤外ではサブミクロン粒子の減光測定が行われる。可視ー紫外では巨視題サ ンプルの反射率、透過率、電子エネルギーロス分光法が用いられる。 |
興味深いのは波長より小さな粒子による減光データと巨視的物質の光学定数
との比較である。我々は Mathis, Whiffen 1989, Ku, Felske 1986 に刺激され
てこの研究を行った。
2.1. Kramers-Kronig 法K-K 関係一般に複素関数 A=Ar - i Ai が E→∞ で A=0 の時、 K-K 関係が成立する。 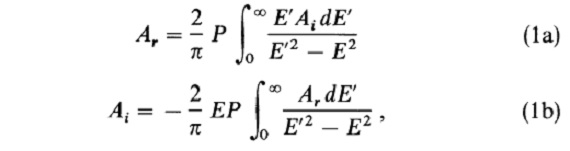 ここに P はコーシーの主値である。A の例としては ε -1 や m-1 が あげられる。ε = εr-iεi は複素誘電関数、m = n -ik は複素屈折率である。 |
分極率 有用な関数は分極率で以下に定義される。 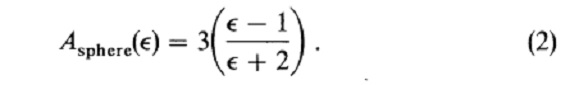 CDE = continuous distribution of randamly oriented ellipsoid |
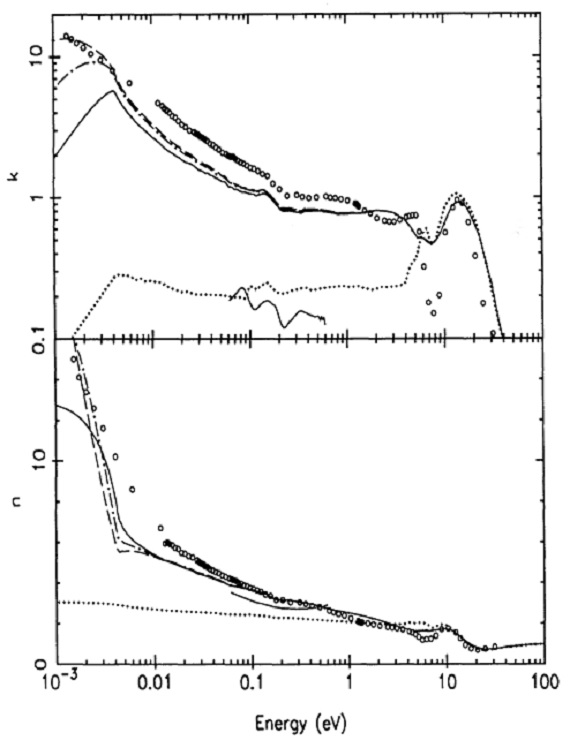 図1.光学定数 上:k、下:n。点線=AC1. 実線=BE1. 点破線=HAPS (df=3, fa=0.35). 破線=FC21PS (df=2.1, fa=1, R/fa=4.782). 様々な集団を仮定して導いた BE 光学定数は 0.01 eV 以上ではよく似ている。 データの無い低エネルギー側では値が散らばる。 白丸=ガラスカーボン(Edoh83)下側の実線=放電形成非晶質炭素 |
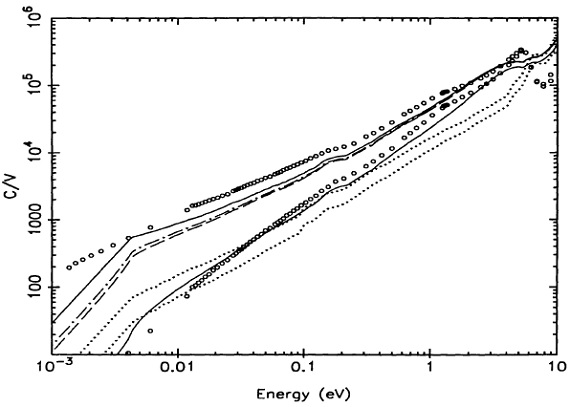 図2.C/V = 単位体積当たりの吸収断面積。 C/V に単位面積当たりのダスト体積を掛けると光学的深さになる。 上実線=BE1 光学定数の孤立 CDE 粒子モデル。下実線=孤立球モデル。 点破線= HAVS (df=3, fa=0.366).破線=FC21PS (df=2.1, fa=1, R/fa=4.727). 上下点線=AC1 孤立 CDE と球。 上下白丸=グラスカーボン 孤立 CDE と球。 AC サンプル Bussoletti87 の AC サンプルはアルゴン雰囲気中で炭素電極間放電を行い ススを形成した。彼らはそれをポリエチレン錠剤に封じ込めて FIR 測定を、 KBr錠剤で 赤外、可視測定を行った。 高エネルギー E=4-30 eV では Fink84 サンプル1を使用した。 E > 60 eV では Henke82 を使った。 BE サンプル BE サンプルは空気中でベンゼンを燃やして得たススである。BE の吸光は AC よりずっと強い。 n, k 図1には 得られた n, k を示す。 |
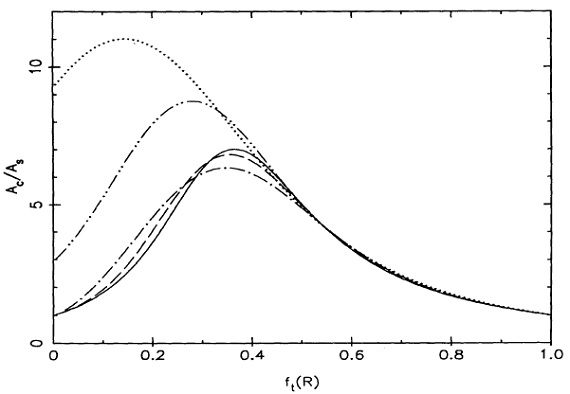 図3.Ac/As の増加。 |
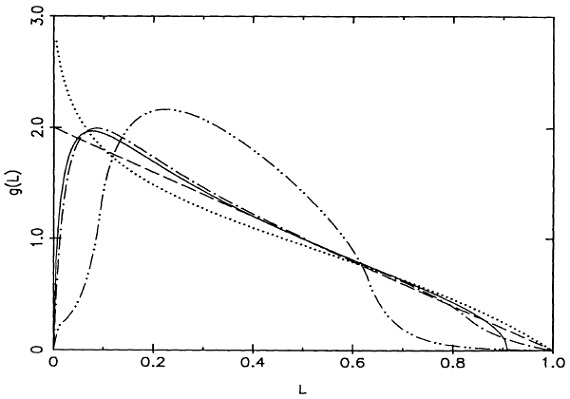 図4.幾何学パラメタ L の分布 |
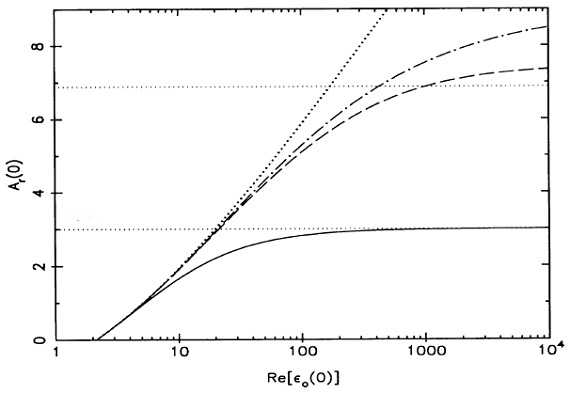 図5.分極率の実数部。 |
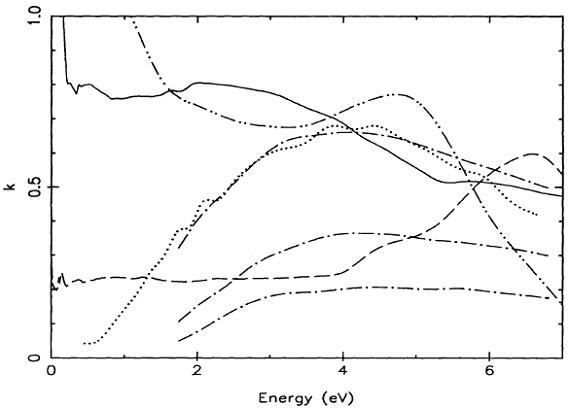 図6.様々な材料の k |