アブストラクト[Fe/H] 勾配-2.8° ≤ l ≤ +0.1° 銀河系短軸沿いの7箇所で K, J-K 色等級図を調べた。上部 RGB の傾きから -2.8° ≤ b ≤ -0.8° で ⟨[Fe/H]⟩ の銀緯による変化は -0.085±0.033 dex/deg と分かった。Tiede et al のデータを合わせると、 -10.3° ≤ b ≤ -0.8° では、傾きは -0.064±0.012 dex/deg である。この関係を 銀河中心まで外挿すると、[Fe/H] = +0.034±0.053 dex となる。 |
吸収強度とその分散 調査した内側バルジでは AK = 0.27 - 2.15 であった。これは E(B-V) = 0.44 - 3.46 に相当する。平均減光強度とそこでの星ごとの減光の 分散との間には線形の関係があり、 σK = 0.056(±0.005) ⟨AK⟩ + 0.043(±0.005) であった。これはフィールドの大きさ(約90") よりも吸収雲のサイズが小さいためと解釈される。 若い種族 最後に、明るい巨星の光度関数から、銀河中心から離れると若い種族 は他よりも急激に数を減らし、1° 以上離れると実際上検知されなく なることが分かった。 |
|
メタル量分布 これまで赤外観測は主に |b| > 3° の可視観測も可能な領域で 行われてきた。その利点は赤外観測に可視観測データで較正が可能で あることである。その結果、例えば Tiede et al 1995 は球状星団の [Fe/H] と巨星枝の勾配を適用して、短軸沿い、 -12° ≤ b ≤ -3° で [Fe/H] 勾配を -0.060±0.033 dex/deg と定めた。 もっと内側へ そのためには近赤外観測が必要。解析方法は球状星団と外側バルジで 確立した。近赤外データから光度関数、赤化、分光に適当な明るい候補星 が選べる。 この論文の目的 この論文の目的は b = -4° より内側の 11 個所での近赤外色等級図 を予備調査することである。うち7つは短軸上、5つは l = -1.3° 上 にある。 |
減光の決定 まず、減光を決定する。その方法は Narayanan, Gould, DePoy 1996 と同じである。 メタル量を決める 次に、各フィールドのメタル量を決める。それには巨星枝 勾配法を用いる。これから、以前に得たバルジ勾配の値を改良することが できる。と言うのは、以前は内側バルジからは一点しかデータがなかった からである。この方法は分光ほど精密ではないが、様々な方向からメタル 量を決めることは大事である。 メタル量の表記について ここでメタル量として [Fe/H] を用いた。ここでのメタル量決定の基礎となる 球状星団では実際に Fe の存在量が決められている。しかし、非太陽型の組成 パターンが巨星枝の傾きに影響するかもしれない。 光度関数 光度関数の先端部分を見ると、バルジでの星形成が継続してきたのか どうかを素早く調べられる。 |

|
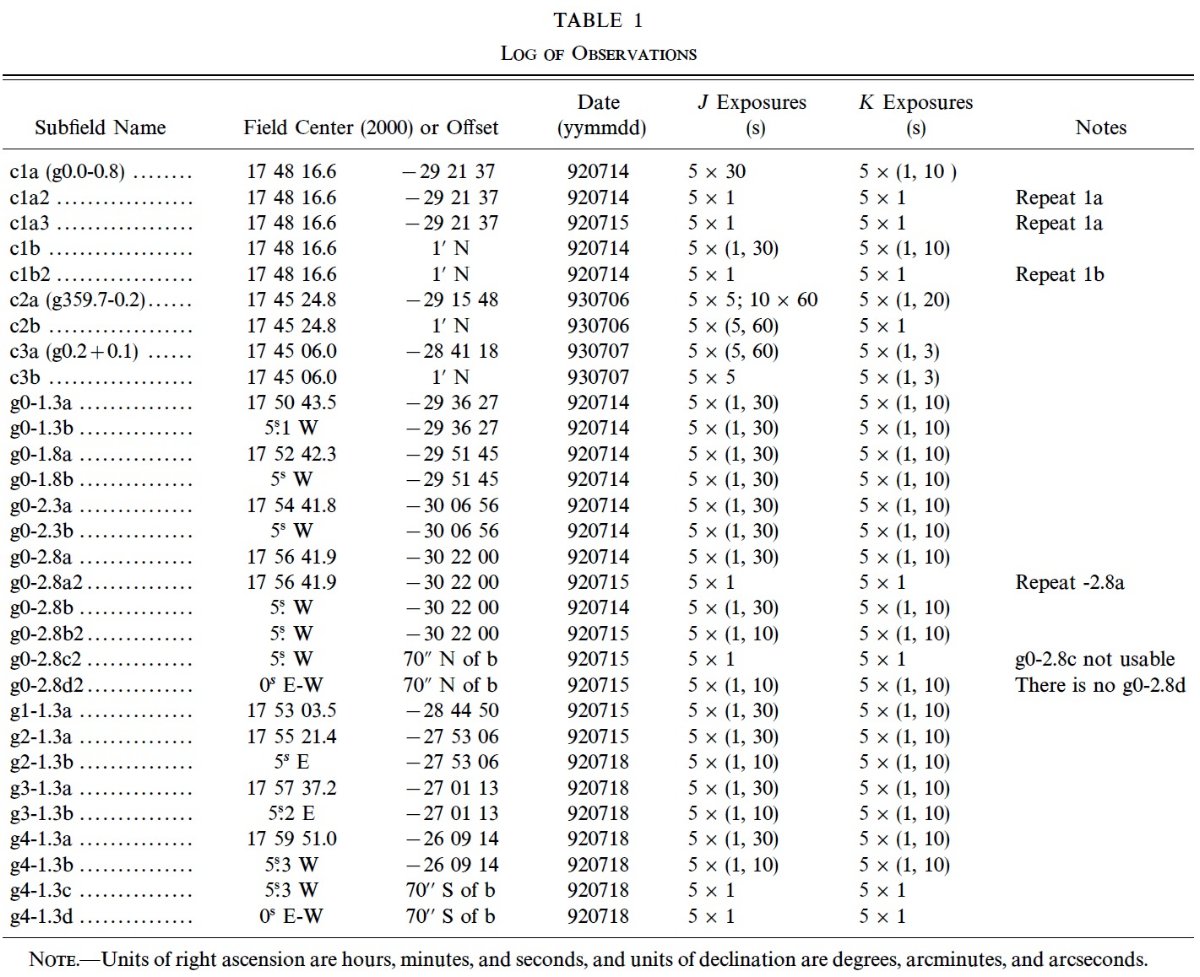
観測 観測は 1992-1993 デュポン望遠鏡 IRCAM/256×256 NICMOS3 を使って 行われた。表1に観測ログ、図1に観測位置を示す。 銀河中心付近の3か所(cが付いている)の選択は Glass et al 1987 (初めは Catchpole 1985)の画像 から眼視で減光の一様そうな箇所を選んだ。ただし、それでも高銀緯に 較べると減光が入り混じっている。これらはキャッチポールフィールドと 名付けた。 観測戦略 視野が狭いので、最初(表1で"a" とついている)は長い露出だが、 b, c は 短時間露出で行った。これは我々が必要とするのが上部 RGB で明るいからである。 等級較正には単素子測光が行われたバーデ窓の2か所を使った。 |
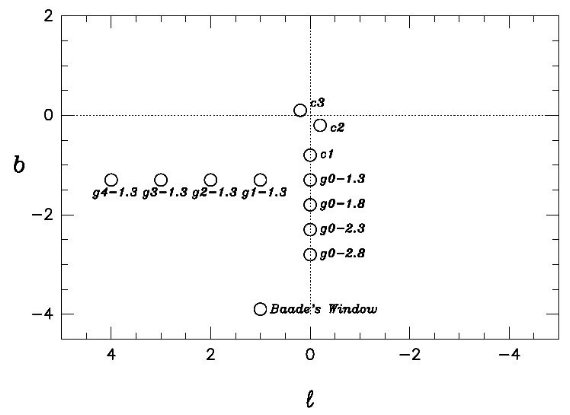 図1.11観測位置。点線は主軸と副軸。バーデ窓の位置も示した。 |
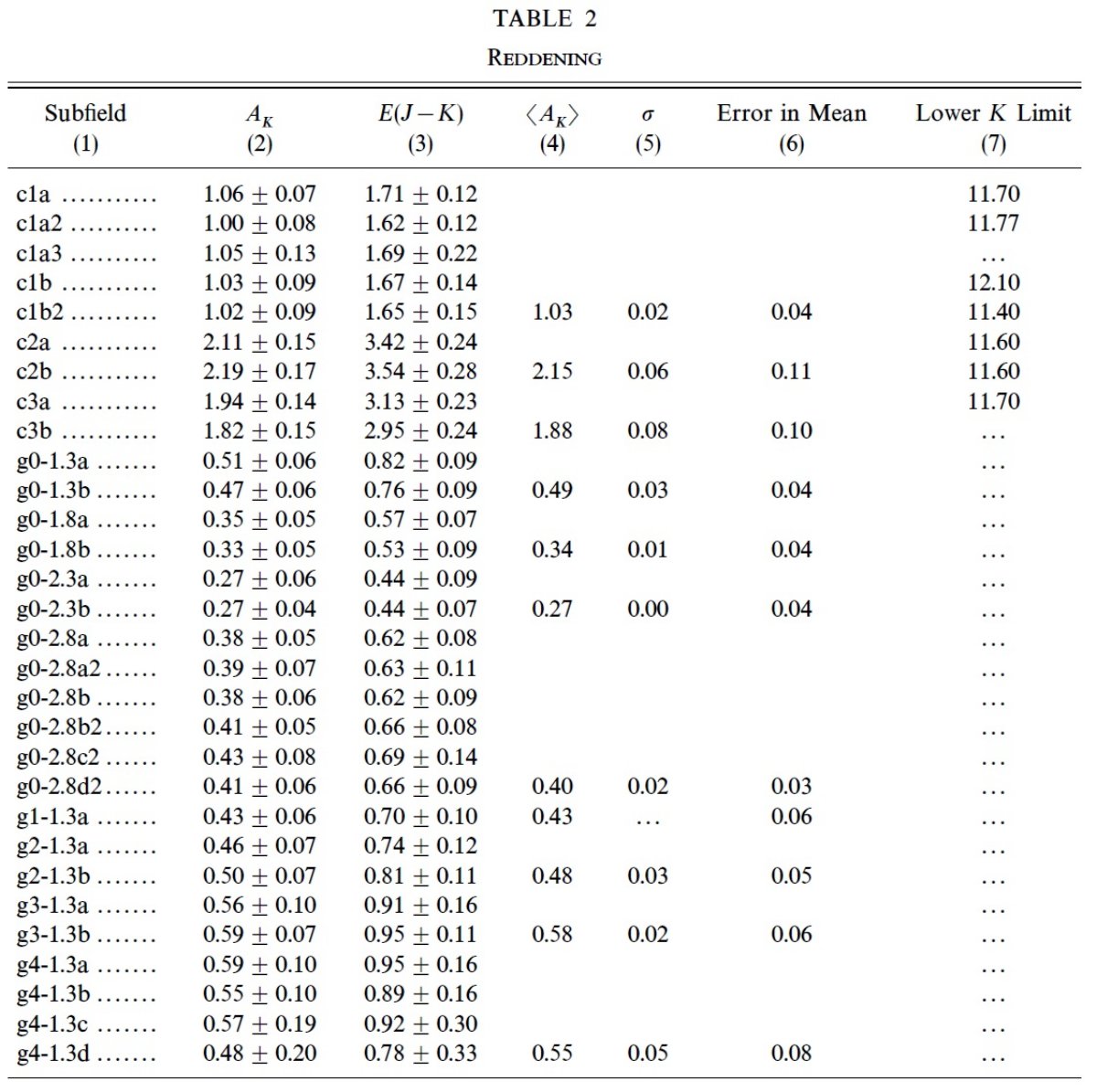
3.1.赤化巨星枝と減光ベクトルを仮定 仮定: 観測領域の上部巨星枝(8<Ko<12)は直線でバーデ窓と同じ。 明るい方のカットは AGB を除くため。暗い方のカットはクランプ星を除くため。 この領域では巨星枝は以下のように表される。 (J-K)o = -0.113(±0.005)Ko + 2.001(±0.052) 係数は Tiede et al のバーデ窓データから決めた。Mathis 1990 の AK = 0.618 E(B-V) も採用した。 減光の決定 観測領域内の星一つずつから減光ベクトルを(逆に)伸ばし、バーデ窓 の巨星枝にぶつかるまでの長さから減光量を決める。2σクリップで前景星 を除去する逐次近似を繰り返して収束値を求める。各サブフィールドの 赤化を表2の第2,3列に載せた。不定性は副領域内の星同士の減光の 分散である。 減光の大きい箇所の問題 減光が大きいと赤い星の J 等級が測れなくなる。そのようなところでは 見かけ上より浅い減光が得られてしまう。そこで、減光の大きなサブフィールド では暗い方の限界を上げて、上部巨星枝に選択効果が効かないようにした。 表2の最後の列はそのような場合に採用した限界等級である。 c1 フィールド 図2は c1 フィールドを示す。 ここは低銀緯で穏やかな減光を示す。実線は脱赤化したバーデ窓巨星枝 で、 c1 星は表2にある値で脱赤化されている。点線より下と実線の上端 より上の星は赤化決定から省かれている。右パネルでは J バンドが浅かっ たので Ko > 11.07 は省かれた。黒丸は減光評価に用いられた。この ように穏やかな減光だと、脱赤化した色等級図上これらの星はバーデ窓 巨星の上部巨星枝に沿って分布する。上部巨星枝がうまく再現できたという 形態学上の成功もこの方法での減光評価が有効であることを裏付ける。 c2 フィールド 図3は c2 フィールドを示す。ここでの減光が最も強かった。J バンド の不完全性のため、c2a では Ko > 9.49, c2b では Ko > 9.41 の星が減光評価に使えなかった。このように最悪の条件でも 二つのサブフィールド間での減光の差は AK で 0.08 しか 違わなかった。この差はエラーの半分にしか当たらない。 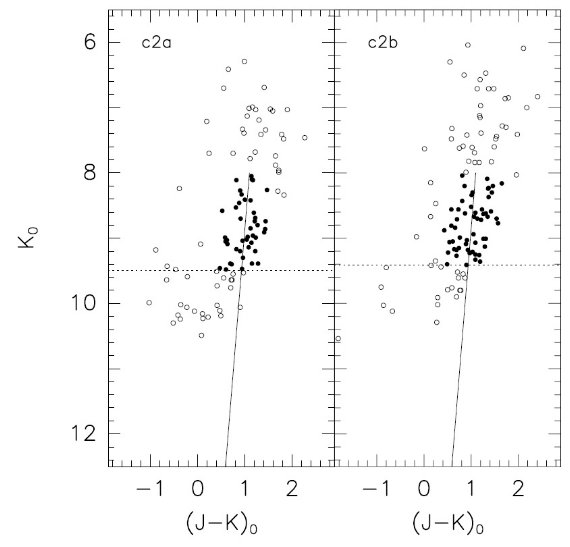 図3.c2 フィールド中の2サブフィールドでの (K, J-K)o 図。 ここは本研究では最も減光が大きかった。また、TRGB より明るい星を 多数含む。 図3では図2,4に比べずっと明るいところまで星が分布する。 これは、減光の結果サチュレーションが抑えられたためである。 |
g0-2.8 フィールド 図4は g0-2.8 フィールドからの例を示す。ここは測光が最も深い等級 に達した g-フィールドの代表例である。恒星密度が低下しているため 色等級図上の上部巨星枝はあまり星が多くない。その代り J バンドの星が 暗い方まで検出できたので明るい方の星数低下を補っている。その上、 サブフィールド内での微分減光が減ったので平均赤化の測定精度は向上した。 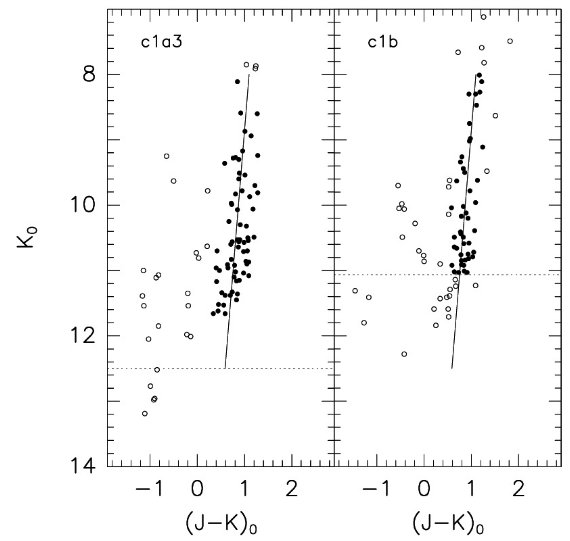 図2.c1 フィールド中の2サブフィールドでの (K, J-K)o 図。 ここは副軸上最も低い箇所。減光は E(J-K) = 1.67±0.15 実線=バーデ窓の脱赤化巨星枝ライン。 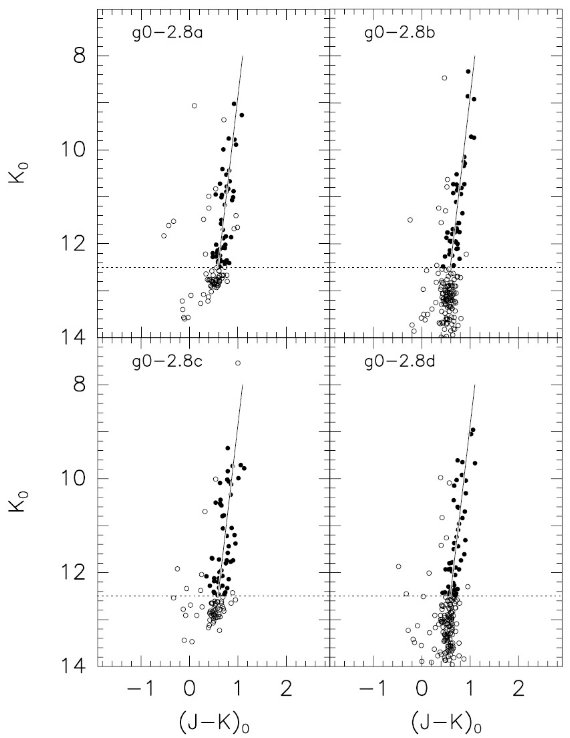 図4.普通のフィールド例として g0-2.8 を選び、そこの 4 サブフィールド での (K, J-K)o 図。b-, d- サブフィールドは a-, c- サブフィールドより 深い。図2,3に比べ数が少ないのは銀緯が高くなったからである。 |
3.2.微分赤化K 平均減光と 1σ 分散の関係銀河中心付近では減光ダストの非一様な分布による微分赤化は恒星種族 の研究を赤外でさえも難しくする。図5はサブフィールドの K 平均減光と そこでの 1σ 分散の関係を示す。このプロットから以下の関係が 得られる。 σ(AK) = 0.056(±0.005)⟨AK ⟩ + 0.043(±0.005) 切片 0.043 は測光エラー 0.05 に大体同じである。 赤化の差と星間距離の相関 星同士の赤化の差と星間距離の相関も調べたが見出せなかった。これは 減光が有意に変動するスケールが数 arcsec 程度またはそれより小さいこと を意味する。 ( この関係の係数と 測定に採用したサブフィールドの大きさから変動スケールが出るか?) |
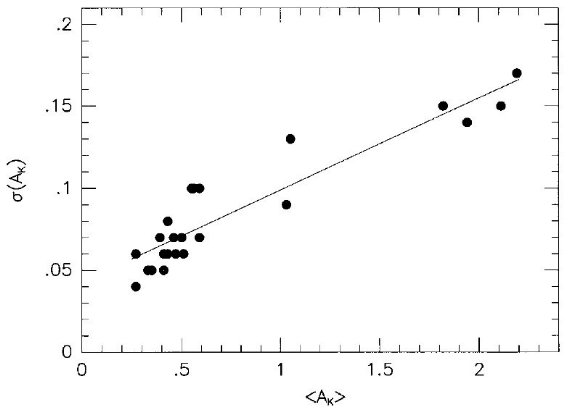 図5.サブフィールドの K 平均減光とそこでの 1σ 分散の関係。 AK の分散が AK に比例する。 ( この関係は測定に採用した サブフィールドの大きさに依存するのだろうな。) |
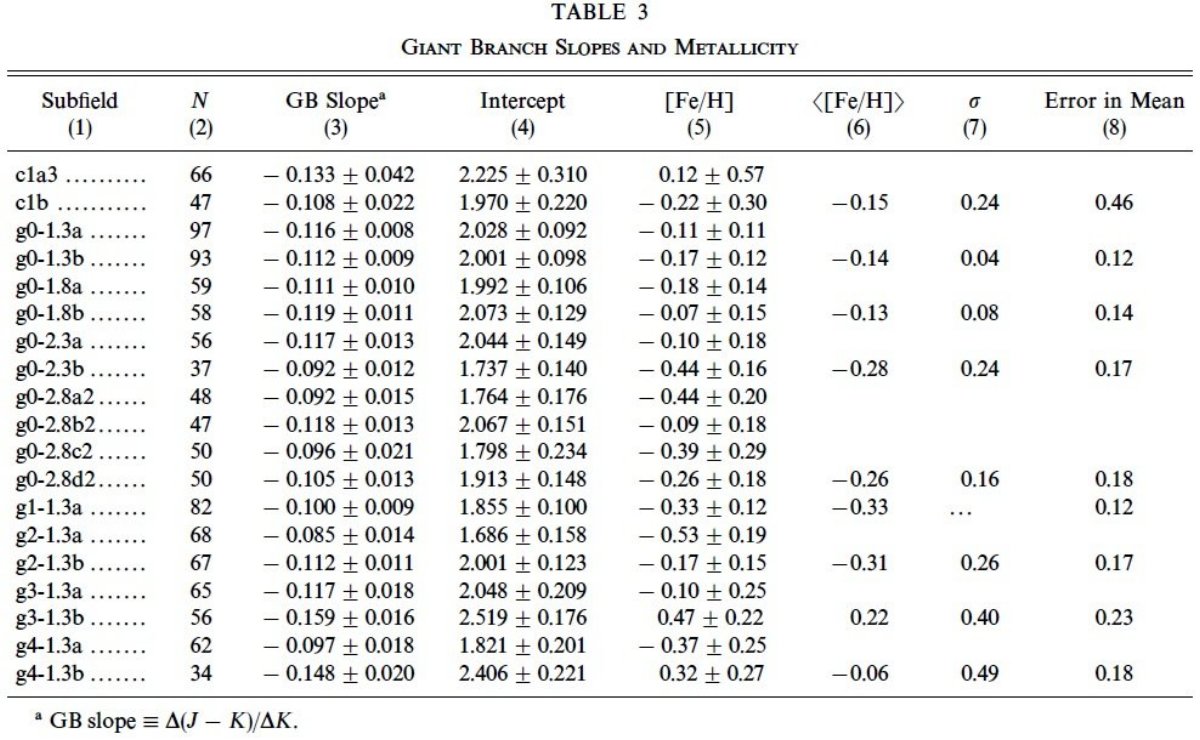
3.3.メタル量上部巨星枝の傾きKuchinski, Frogel, Terndrup 1995 は項メタル球状星団では上部巨星枝の傾きがメタル量とよく相関することを 見出した。しかし、今回のように赤化が大きな領域では、異なる測光システム 間のカラー変換に伴う不定性が勾配の比較に影響を及ぼす可能性がある。これ は巨星枝に沿っての J-K カラー変化が約 0.5 等あるからである。 ( 勾配の比較にどうして 赤化の大きさが関係するのか分からない) メタル量 色等級図上の巨星枝に直線フィットして得た勾配から得られたメタル量 を表3に示す。 ここではメタル量を [Fe/H] と名付けているが、鉄に対する他の元素の 組成が球状星団とバルジで変わっている可能性は考慮していない。従って 得られた値がその影響を受けている可能性はある。 |
サブフィールド サブフィールド c2, c3 は除外された。減光も微分赤化も強く、巨星枝 が激しく丸められてしまい、勾配の決定も前景星の排除も困難になっている からである。サブフィールド g4-1.3c, は星数が少なく前景星の混入を 確実に評価できないため除去した。 バルジ星の勾配 - メタル量関係 バルジ星の勾配メタル量関係には Tiede et al 1997 の次の式を用いた。 [Fe/H] = -1.692(±0.500) - 13.613(±5.118)勾配 Kuchinski, Frogel, Terndrup, Persson 1995 の関係式を再較正したこの式はバルジ短軸沿いの5点での観測に基づいている。 しかし、 Tiede, Martini, Frogel 1997 Tiede et al 1997 の表2を見ると分かるがバルジ星に対し、特に [Fe/H] ≤ -0.4 では再較正が必要である。 ( 上の式はおそらく年齢効果による 巨星枝勾配 - メタル量関係のラインシフトを表す再較正。しかし、 Tiede et al 1997 論文にはバルジの5点、特にそのメタル量がどこから来たのか、の出所 が書いていない。) |
|
内側バルジのメタル分布 図6は短軸に沿った ⟨[Fe/H]⟩ - b プロットである。実線は エラー重み付きのフィットで勾配は -0.085(plusmn;0.033) dex/deg、 b = 0 での値は -0.019(plusmn;0.066) である。この値は Tiede et al 1995 が主に外側バルジ b = -12° から -0.2° までの勾配をもとに得た -0.066(plusmn;0.033) と合致する。 結合メタル分布 この一致に鑑みて、Tiede et al 1995 データと今回のデータを結合する ことにした。ただし、Tiede et al 1995 データは 3.3 節の再較正した 式で出したメタル量を適用する。エラー重み付きフィットの勾配は -0.064±0.012 dex/deg で b = 0° の値は +0.034&plumn;0.053 dex である。 ( 前にも書いたように 再較正式のデータの出所が 1997 論文では不明。) 銀緯とそこでの ⟨[Fe/H]⟩ を表4に示した。b = -12°.5 フィールドは除外した。Tiede et al 1997 に書いてあるが ハロー/薄い円盤 の混入が激しいからである。 ( どこか不明だった。) 図7に新しい結合データによるメタル分布を示す。 メタル量分布の巾 この結果、銀河中心付近のメタル量は太陽に近いことになる。これは、大質量 楕円銀河よりは低質量楕円銀河に近く、それから推測すると、 Ti や O が 選択的に増大しているかも知れない。最近の Ramirez et al 1997 の 銀河系中心の星の高分解能分光によると [Fe/H] = -0.07 ±0.11 で上の結論にマッチする。どうやら、バルジは円盤や ハローより速くメタル量を増加させたが、最も最近の星形成でさえも 超太陽組成には辿りつかなかったようだ。 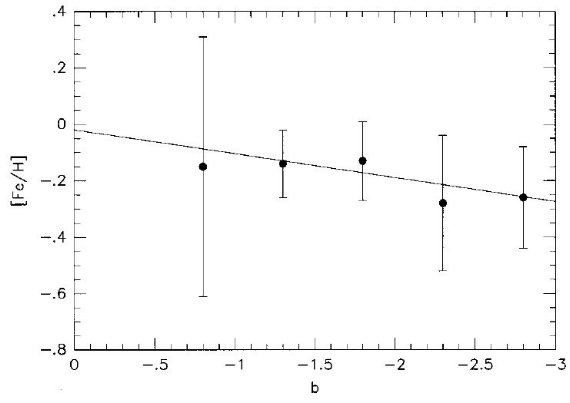 図6.短軸に沿ったフィールド平均メタル量と銀緯の関係。データは表4から。 曲線=エラー重み付きフィット。勾配は -0.085(plusmn;0.033) dex/deg |
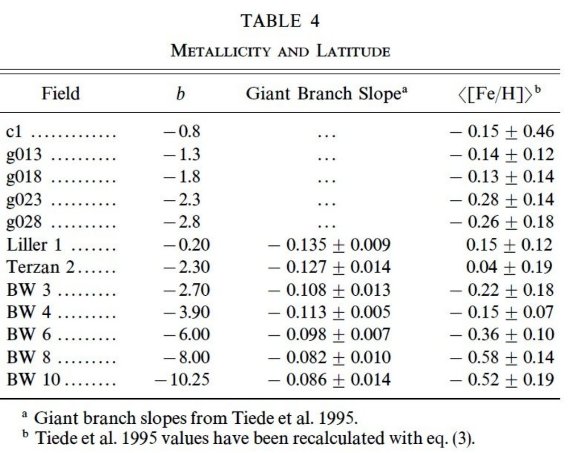 表4.メタル量と銀緯の関係。 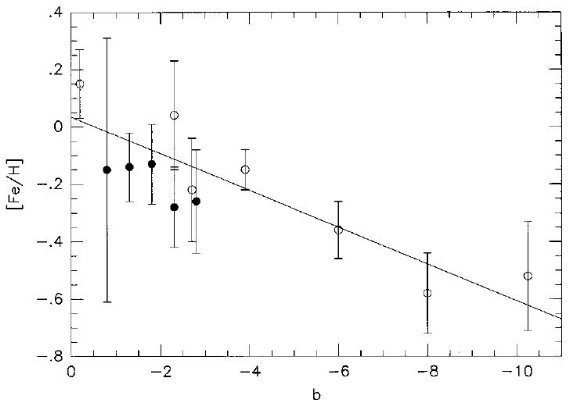 図7.白丸=短軸に沿ったフィールド平均メタル量。黒丸= Tiede et al 1997 のフィールド。 曲線=エラー重み付きフィット。勾配は -0.064(plusmn;0.012) dex/deg で 銀緯=0での切片は [Fe/H] = +0.034(plusmn;0.053) dex である。 |