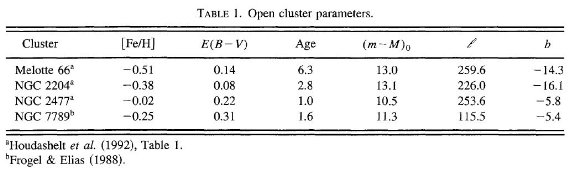
表1.NIR 観測のある散開星団
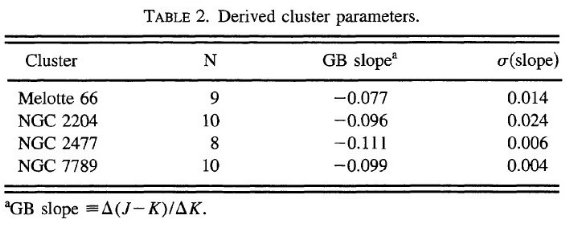
表2.散開星団巨星枝の結果
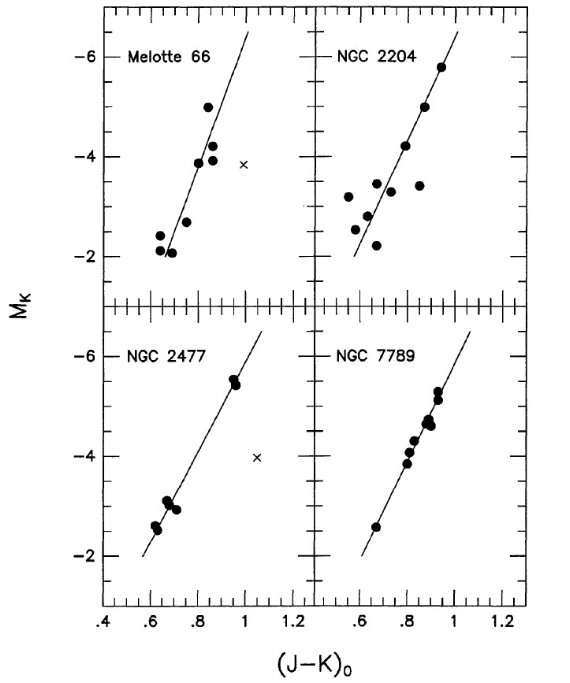
図1.星団巨星の色等級図。X 印は 2σ ではねられた。
アブストラクトKuchinski et al 1995 の導いた 巨星枝勾配 (Δ(J-K)/ΔK) - [Fe/H] 関係を散開星団に 適用した。散開星団でも高メタル球状星団と同様に、K-(J-K) 色等級図での 巨星枝勾配 が [Fe/H] と相関することがわかった。ただし、同じ [Fe/H] で 見ると、散開星団の勾配は系統的により負ではない方向にシフトする ことが分かった。( 立つの?寝るの?どっち?) モデル等時線を用いてこの関係の基礎を調べた。ある [Fe/H] に対して、 関係の傾きは年齢が若くなっても一定であるが、関係は年齢が若くなると より負でない巨星枝の勾配にうつることが分かった。 ( 全くわかんない。) モデルが予言するこの二つはデータにも合致する。最後に、3つの星種族、 高メタル球状星団、バルジ星、散開星団に対して、巨星枝勾配 - [Fe/H] 関係 の新しい係数を決めた。 ( バルジデータの出所が不明。) |
1.イントロKuchinski,Frogel,Terndrup, Persson 1995 は高メタル球状星団で巨星枝勾配とメタル量の関係を導き、Kuchinski, Frogel 1995 はそれを以下の式に改定した。[Fe/H] = -2.98(±0.70) - 23.84(±6.83)勾配 (1) この式のエラーは ±0.25 dex である。Tiede et al 1995 はこの関係を バルジ短軸沿いの 8 点に応用して、他の方法で決めたメタル量と ±0.29 dex で一致することを見出した。 この論文では散開星団に拡張する。 |
散開星団の観測例は少ない。表1にそれらを示す。解析の方法は
Kuchinski et al 1995 に倣う。それぞれの論文から距離と赤化を得て、
補正を施し、 -6.5 ≤ MK ≤ -2 の上部巨星枝の
星を選ぶ。これはレッドクランプ星と AGB 星を除くためである。
また、メンバーでないとされた星も除く、こうして残った巨星が
8つ以上の星団4つを扱う。図1にそれらの色等級図を示す。 表1.NIR 観測のある散開星団  表2.散開星団巨星枝の結果 |
 図1.星団巨星の色等級図。X 印は 2σ ではねられた。 |
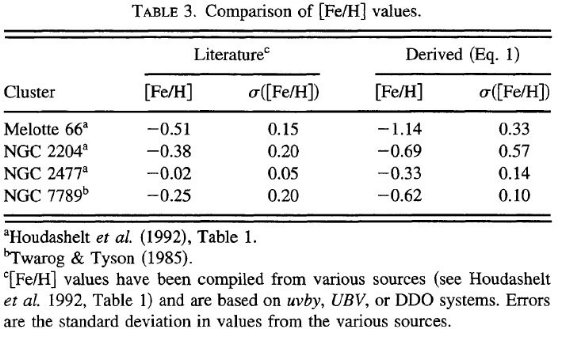 表3.文献からと巨星枝の傾きから決めたメタル量 種族による関係式の違い 表3には文献から採ったメタル量を巨星枝の傾きと式1から決めた メタル量を示す。 図2(a) には文献から採ったメタル量を巨星枝の傾きと比べた。 実線は上に記した式から求めた球状星団のメタル量である。図を見ると 関係の勾配は三つの種族で似ているが、同じ [Fe/H] で比べると 散開星団の巨星枝は色等級図でより立っていることがわかる。それよりは 弱いがバルジ星も同様の傾向を示す。 ( バルジデータの出所が不明。) 第2パラメタ― 種族により関係式に違いが出るのは第2パラメタ―の存在を示唆する。 Kuchinski et al 1995 はそれが年齢ではないかと考えたが、 10 ≤ t(Gyr) ≤ 16 では年齢による勾配変化はメタル量による 変化に比べると無視できるほど小さいことが分かった。しかし、 散開星団の年齢は 10 Gyr よりずっと若い。従って、1 ≤ t(Gyr) ≤ 16 の範囲でモデルと比較する作業が必要となる。 この上限値 16 Gyr は Kuchinski et al 1995 の範囲に、下限値 1 Gyr は巨星枝勾配と [Fe/H] との相関が保持されると想定される限界である。 等時線モデル(1)J-K カラーの計算 勾配と年齢の関係をもっと知るため、イエール等時線 (Y96) を用いて t = 1, 2, 3, 5, 19, 16 Gyr, [Fe/H] = 0.0, -0.3, -0.7, -1.3 の組み合わせで等時線を得た。Y96 には J, K 等級がないので Te から、 モデル大気(Cohen et al 1978)の結果を用い、 (J-K) = 259.44 - 137.72logTe + 18.31(logTe)2 からカラーを決めた。問題はこの式が 3.58 ≤ logTe ≤ 3.72 で しか使えないことで、冷たい logTe ∼ 3.52 の星には外挿する必要が ある。ただ、これは [Fe/H] ≥ -0.3、t > 5 gyr の星にのみ 必要である。 また、それらの場合でも外挿が必要となるのは TRGB から 1 mag 以内の星のみである。 |
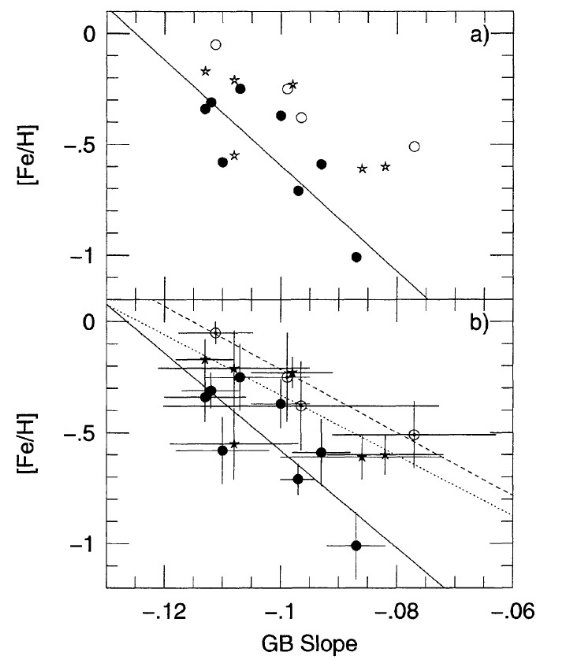 図2.[Fe/H] と勾配の関係。黒丸=球状星団。星印=バルジフィールド。 白丸=散開星団。 (a): 実線=Kuchinski et al 1995 の球状星団関係。 (b): 同じデータだが、エラーバーを付けた。エラーで重みを付けてフィットした。 実線=球状星団。点線=バルジ星。破線=散開星団。 ( バルジデータの出所が不明。) 等時線モデル(2) BCK 高メタル球状星団に関する Frogel et al 1983 から輻射補正を次 のように決めた。 MK = -21.89 - 2.5log(L/Lo) + 6.70log(Te) |
|
等時線モデルと球状星団 図3には等時線モデルから決めた [Fe/H] と 巨星枝勾配の関係を 示す。図の各線は特定の年齢に対応する。J, K の決定が上に 述べたように不完全なため、図2との完全な一致は期待できない。 我々が関心を持つのは、ある [Fe/H] に対して年齢によって巨星枝 勾配の相対的変化である。最も左の2本は 16, 10 Gyr である。 球状星団はこの狭い幅の中にいる。年齢変化に対して勾配が殆ど 変化しないことが明らかである。 等時線モデルと散開星団 散開星団では事情が異なる。古い散開星団の年齢は 10 Gyr と 1 Gyr の間にある。この範囲では、年齢変化とメタル量変化は巨星枝勾配に 対して同じくらいの影響を持つ。この年齢効果は図2で見た傾向を 説明するのに役立つかも知れない。 年齢グループ t(散開星団) < t(バルジ) < t(球状星団) と考えると、 図2の系統的なシフトは定性的には自然に理解できる。この 系統的シフトはまた、なぜ球状星団で決めた勾配 - メタル量関係 を散開星団に適用した時 [Fe/H] を少なめに決めたかの説明を 与える。しかし、我々はこの三つ、年齢、[Fe/H]、勾配、の間の 関係に観測的な表現を与えることはできなかった。データが少なすぎる からである。その上、モデルにも問題がある。例えば、図2の球状星団 を図3と照合すると、球状星団の年齢は 1-3 gyr にあることになる。 巨星枝勾配 - メタル量関係の勾配 表4には、巨星枝勾配 - メタル量関係の勾配を散開星団、バルジ、 球状星団でエラー重み付き直線フィットした係数を示した。等時線から 求めた係数も載せた。 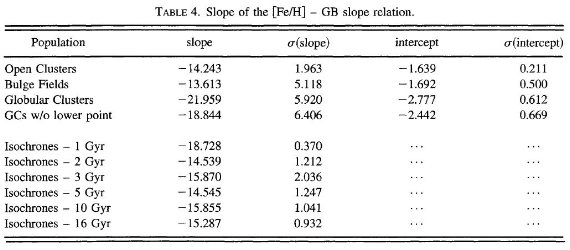 表4.巨星枝勾配 - メタル量関係の勾配 |
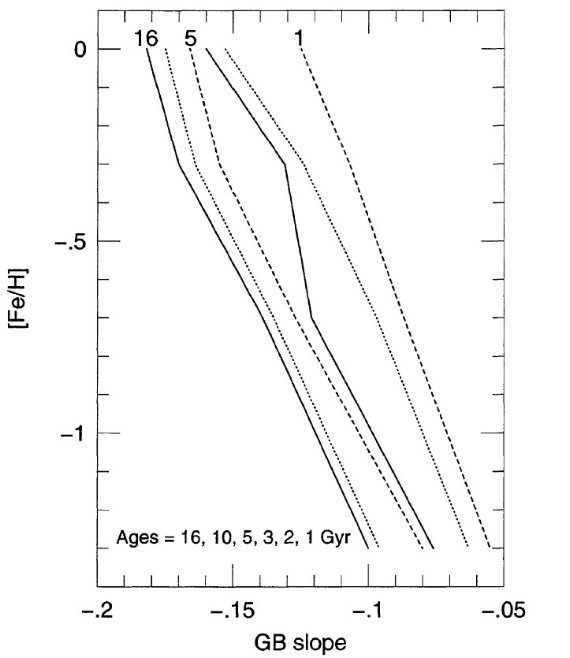 図3.等時線モデルから決めた [Fe/H] と 巨星枝勾配の関係。 |
| 散開星団の巨星枝勾配 - メタル量関係は球状星団に対する それと似ているが横にシフトしている。このシフトの原因を 探るため、等時線モデルのグリッドを調べた。 その結果、年齢効果がシフトの原因らしいことが分かった。 | しかし、定量的な説明のためには、データが少なすぎ、またモデルが まだ不十分である。 |