Low Extinction Windows in the Inner Galactic Bulge

　２．低減光の窓の選択　

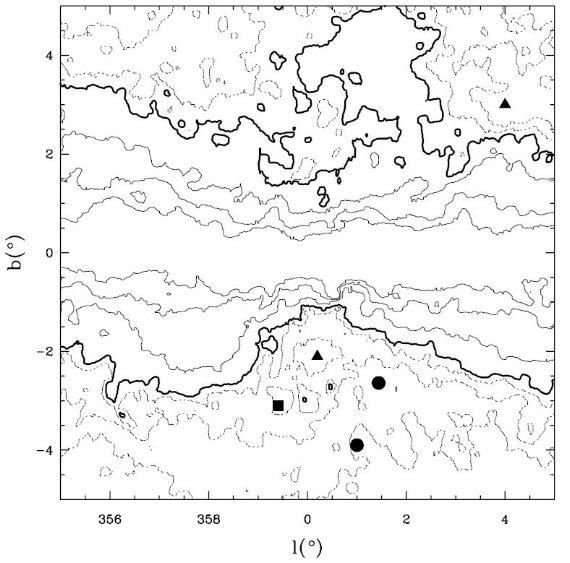
FIR 放射から決めた K 減光　 Schlegel et al. 1998 のサイト、http://astro.berkeley.edu/dust から FIR 放射で 決めた減光データを取り込んだ。ここから得た K バンド減光を AK,FIR と呼ぶ。 　FIR 減光による低減光窓候補　 　 Stanek et al. 1998 は FIR 減光マップから (l, b) = (0°, -2°), (4°, -3°) を中心とする二つの 低減光の窓を見つけた。FIR 減光は視線方向銀河の果てまでのダスト全体から の寄与を含むが、それでも遠赤外減光の角度変化は潜在的に有望な低減光 領域を選択する際の助けとなる。 　我々は Stanek et al. 1998 からオリジナルの FIR マップを取りだし、E(B-V)FIR を計算し、 銀河中心周り 10°×10° のマップを作った。図１にそのマップ を窓の位置と共に示す。 　減光の変換には、AK = 0.112 AV, RV = AV/E(B-V) = 3.1 (Cardelli et al 1989) を用いた。 　表１には上述のバルジ窓のパラメタ―を示す。 図１．銀河中心周り 10°×10° のマップ。AK,FIR の値は、点線 = 0.7, 1.05, 1.4. 太い実線 = 1.75. 細い実線 = 3, 6, 10. 黒丸 = Baade 1963 による低減光窓。 三角＝Stanek 1998 の低減光窓。四角＝今回の窓。 ( 横軸の向きが普通と逆に注意。)

　３．候補の窓内部における減光　

３．１．FIR 減光マップ　 　 W0.2-2.1 窓　 　図２には (l, b) = (0°, -2°) 周囲 2° 以内の AK,FIR マップを示す。この図には表１にある W0.2-2.1 窓が含まれる。この窓の存在は Stanek 1998 が最初に指摘した。実際我々はこの窓の位置を (l, b) = (0.25°, -2.15°) でサイズ 60'×40' とより細かく決めた。 窓では ⟨AK,FIR⟩ = 0.41 で マップ内全体の AK,FIR 平均値より低い。 W0.2-2.1 窓内の最低値は AK,FIR = 0.28 である。 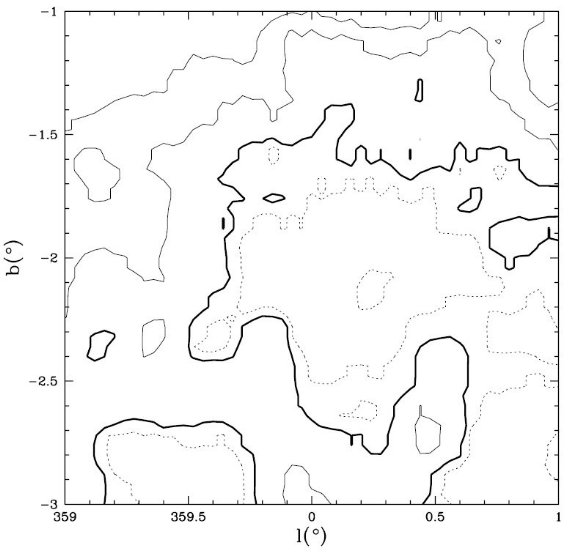図２． W0.2-2.1 窓の FIR 減光マップ。 AK,FIR 値は、 点線 = 0.29, 0.37, 太い実線 = 0.41, 細い実線 = 0.57, 0.83.

W359.4-3.1 窓　 　図３には (l, b) = (-359°, -3°) 周囲、今回新しく提案する W359.4-3.1 窓近傍のマップを示す。はっきりした極小が、 (l, b) = (-359.40°, -3.10°) に認められる。穴のサイズは 40'×30' である。ここの極小値は AK,FIR = 0.24 である。 マップ領域の平均は、 ⟨AK,FIR⟩ = 0.42 で、その 2.5 std. にあたる。図１を見ると、図の領域全体が銀緯の割に低減光で あることが分かる。 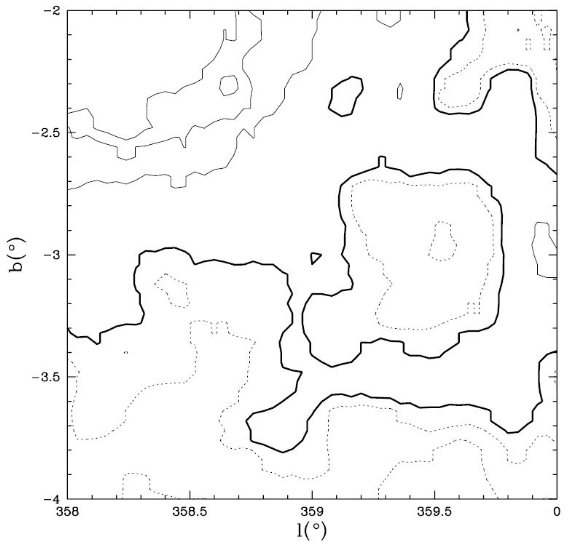図３． W359.4-3.1 窓の FIR 減光マップ。 AK,FIR 値は、 点線 = 0.31, 0.38, 太い実線 = 0.42, 細い実線 = 0.59, 0.76, 0.87.

３．２．2MASS から AK を導く　 　2MASS データ　 　(l, b) = (0°, -2°) と (-359.40°, -3.10°) の 周囲 1° 以内の 8.0 ≤ Ks ≤ 11.5 2MASS 天体を選んだ。この等級帯 は上部 RGB がバーデの窓と同じくらいによく定義され、かつ直線性もよい 部分として選択された。星の数は W0.2-2.1 で 90,407, W359.4-3.1 で 69,280 個である。比較のために選んだ Sgr I (l, b) = (1°, -3°) と バーデの窓(1°, -4°) 領域では、48,040, 20,358 個であった。 　セル　 　領域を 4'×4' のセルに分割した。各セル毎に Frogel et al 1999 の赤色巨星枝フィッティングの方法を適用して減光を定めた。 ただし、彼らは Tiede et al 1995 の赤色巨星枝を参照用にして バーデの窓の減光分布を定めたが、我々は Frogel et al 1999 の 得たバーデの窓の赤色巨星枝を参照源にした。 　減光の決定法　 　我々の方法は次のとおりである。 （１）．Frogel et al 1999 から７つのフィールド、g0-1.8a, g0-2.3a, g0-2.8a, g1-1.3a, g2-1.3a, g3-1.3a, g4-1.3a, を選ぶ。 （２）．K から Ks への変換は Persson et al 1998、減光則は Cardelli et al 1989 に従う。つまり AKs/AV=0.118, AK/AV=0.112, AK/AKs=0.95 とした。 （３）．赤外赤化と減光の比は Mathis 1990 の AK = 0.618 E(J-K) を使って、 AKs = 0.670 E(J-Ks) とした。 ( AKs = (1/0.95)AK =(0.618/0.95){AJ- AKs + AKs - AK} =(0.618/0.95)[1+E(Ks-K)/E(J-Ks)]E(J-Ks)=? AJ/AV が分かれば計算できるけど。 ) （４）．Frogel et al 1999 の７領域のそれぞれで脱赤化を施し、 その後一つの合成色等級図を作った。図４がそれである。 （５）．図にはっきりと上部赤色巨星枝が浮かび出た。それを直線で フィットした。結果は 　　　　　(Ks)0 = -7.81(J-Ks)0 + 17.83 　　　　(2) 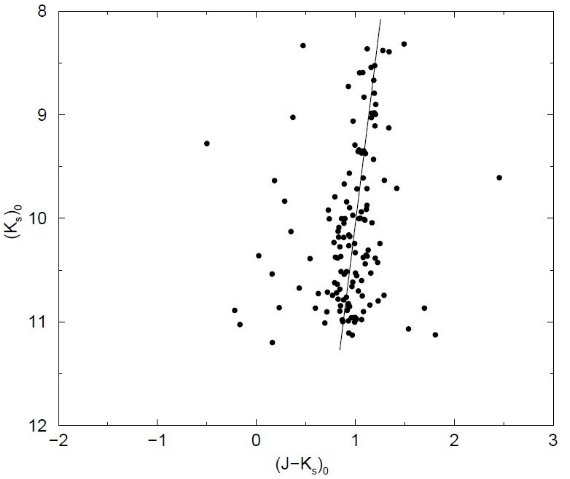図４． Frogel et al 1999 フィールドに おける合成色等級図の上部 RGB.

（６）．セル毎に作った色等級図上、一つ一つの星を（５）の参照 赤色巨星枝から減光ベクトルに沿って移ってきたと看做して、減光 量を計算する。セル内の星の減光量のメディアンをそのセルの 減光量とする。2-σ クリッピングの逐次近似で前景星の混入 を防ぐ。こうして決めた減光を AK,2MASS と呼ぶ。 　W0.2-2.1 と W359.4-3.1 での赤化補正　 　図５(a), (c) には W0.2-2.1 と W359.4-3.1 マップからの典型的なセル における赤化補正後の色等級図を、(b), (d) には AK 分布を示す。 図を見ると AK 分布に第２のピークが AK = 0.14 と 0.02 に存在することがわかる。これは色等級図上、主赤色巨星枝の左側に第２巨星枝 が存在することに対応する。これは第２ダスト層があるためなのか、または 4' より 小さなスケールでのダスト雲の構造のためである。 　Sgr I と バーデの窓での比較　 　Sgr I と バーデの窓を含む低減光参照域に対しても同じ方法を適用して、 AK = 0.23±0.05 と 0.18±0.04 を得た。Glass et al 1995 は Sgr I の変光星を研究し、 AK = 0.21 を適用した。 Stanek 1996 が得た減光マップと Gould et al 1998, Alcock et al 1998 によるゼロ点の較正を考慮すると、バーデ の窓に対しては ⟨AK⟩ = 0.17±0.03 である。 適用した減光決定法と 2MASS 測光のために得られた結果は文献の値と近い。 ( 何のこと？) こうして、内側バルジで減光マップを作ることは有用である。 　銀河中心にもっと近づくと　 しかし、銀河中心にもっと近づくと、星が込み合い、減光の変動が激しくなる。 その結果測光精度が下がり、方法の有用性に問題が生じる。もう一つの 問題はメタル量勾配がどう影響するかである。これが減光量の推定に系統的な 効果をもたらす可能性がある (Schultheis et al 1999) しかし、M 型巨星 の分光観測を用いた最近の Ramirez et al 2000 の研究によると大きな メタル量変化はないらしい。 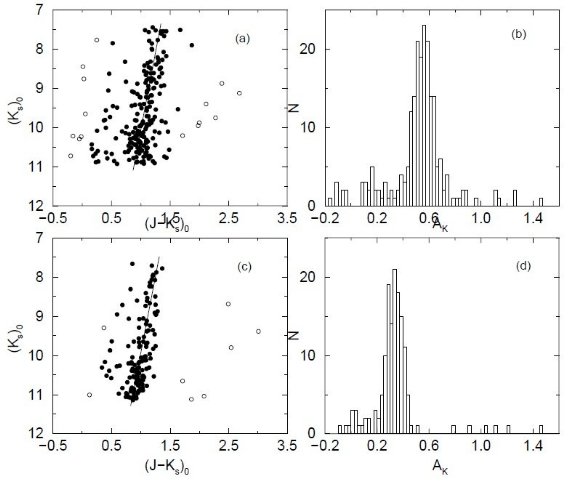図５．(a). W0.2-2.1 (l,b)=(0.07°,-1.2°) セルの (Ks0, (J-Ks)0) 色等級図。白丸＝ ヒストグラム作成の際 2σ クリッピングではじかれた。 実線＝式２の参照用赤色巨星枝。 (b). (a) から導いた Ks ヒストグラム。 (c). W359.4-3.1 (l,b)=(359.2°,-2.2°) セルの (Ks0, (J-Ks)0) 色等級図 (d). (c) から導いた Ks ヒストグラム。

３．３．2MASS 減光マップ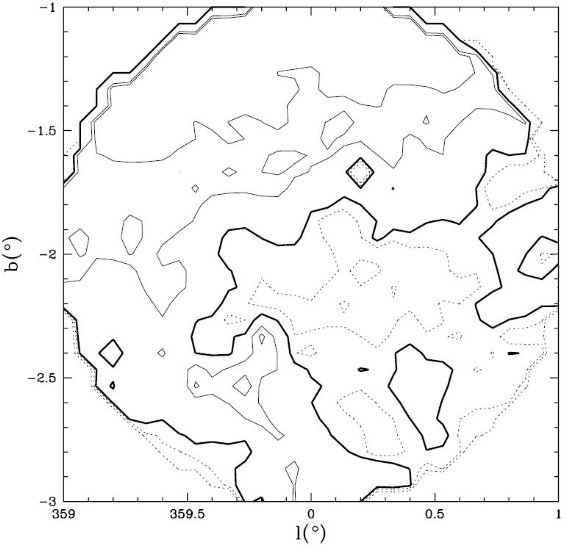　 図６． W0.2-2.1 窓の 2MASS 減光マップ。AK,2MASS 値は、 点線 = 0.2, 0.25, 太い実線 = 0.29, 細い実線 = 0.4, 0.5. 　 AK,2MASS マップ　 　図６は W0.2-2.1 窓の、図７は W359.4-3.1 窓の AK,2MASS マップである。図２、３とよく似ている。どちらも 0.2 < AK,2MASS < 0.25 の窪みを示す。平均減光強度は W0.2-2.1 窓で ⟨AK,2MASS⟩ = 0.29±0.05、 W359.4-3.1 窓で ⟨AK,2MASS⟩ = 0.28±0.04 である。図の隅で等高線が欠けているのは単にサンプルセルが欠けている ためである。 　 AK,2MASS ヒストグラム　 　図８(a), (c) には AK,2MASS ヒストグラムを示す。 W0.2-2.1 窓の方が W359.4-3.1 窓より AK,2MASS の高い星 が多いのは銀河中心に近いためである。 ( 減光は手前のアームが原因では？) 　 AK,2MASS エラー分布　 　図８(b), (d) には AK,2MASS 決定の内部エラーを示す。 W0.2-2.1 窓の方が W359.4-3.1 窓より内部エラーが大きい。これは Frogel et al 1999 でも注意されていた現象で、その領域ではダスト分布の変動スケール が小さいためであろう。エラーの分散は W0.2-2.1 窓で ⟨σ⟩ = 0.09±0.03、 W359.4-3.1 窓で ⟨σ⟩ = 0.08±0.03 である。この平均エラーは Frogel et al 1999 より少し 大きいが、セルの大きさが 1.5'×1.5' から 4'×4' に増加した ためであろう。 　暗黒雲　 　 W0.2-2.1 窓と W359.4-3.1 窓は Sgr I, Sgr II, バーデの窓より銀河中心 に近く、暗黒雲に囲まれたホールに位置する。それらの暗黒雲は LDN48, LDN43, LDN1801, LDN1769, LDN1783, LDN3, LDN1795, LDN1788, (Lynd 1962), FSDN435, FSDN431, FSDN430, FSDN444 (Feitzinger,Stuwe 1984) である。

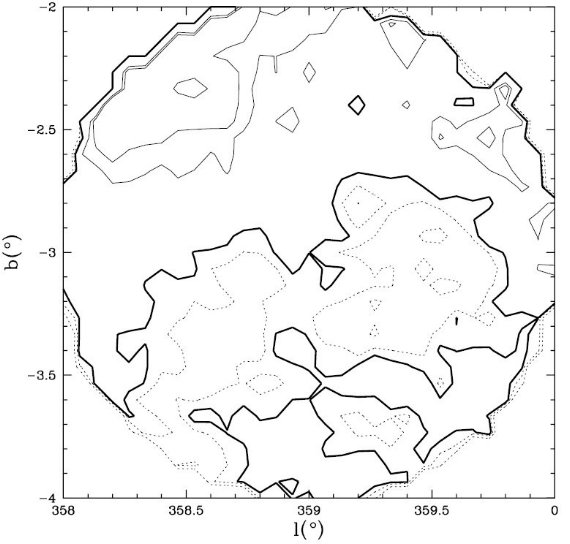図７．W359.4-3.1 窓の 2MASS 減光マップ。AK,2MASS 値は、 点線 = 0.2, 0.25, 太い実線 = 0.28, 細い実線 = 0.4, 0.5 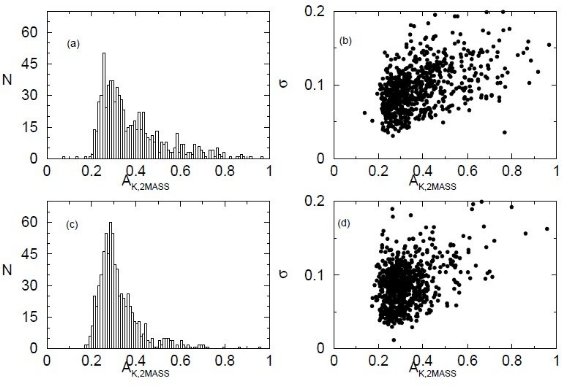図８．(a), (c) には W0.2-2.1 と W359.4-3.1 での AK,2MASS 分布を示す。(b), (d) には 減光値の内部エラー σ と減光値 AK,2MASS の関係を示す。

３．４．2MASS と FIR 減光の比較　 　W0.2-2.1 ではいくつかの枝　 　 Schlegel et al. 1998 マップは分解能 6.1' なので比較のため、 AK,2MASS マップ を σ=4.5' のガウシアンで畳み込んで分解能 6’のマップを作った。 図９にはセル毎の比較を示す。W0.2-2.1 ではいくつかの枝が認められる。 これらの枝はそれぞれがマップ上の特定の個所に対応していた。つまり、 視線上のダスト雲の性質、多分温度や密度、の違いを反映していると考え られる。 　 W359.4-3.1 は線形関係だが、等値でない。　 　W359.4-3.1 は線形関係が認められる。だが、等値でなく、 　　　　　AK,FIR = 1.45 AK,2MASS である。　 Arce, Goodman 1999 は、おうし座暗黒雲で類似の関係を見出した。かれらは、Schlegel らは 減光量を 1.3 - 1.5 倍多く見積もっていると考えている。彼らはまた、 その原因が Rv がおうし座方向で高いためではないとした。なぜなら、 Whittet et al 2001 らによりおうし座暗黒雲ぼ Av < 3.0 領域では Rv = 3.1 が確認されているからである。 　おそらく、　 Schlegel et al. 1998 では、ダストの柱密度 - 赤化関係の較正に E(B-V) ∼ 0.15 程度の 低減光のサンプルを使ったことが違いの原因なのであろう。高減光領域では その関係を適用できないのでないか。 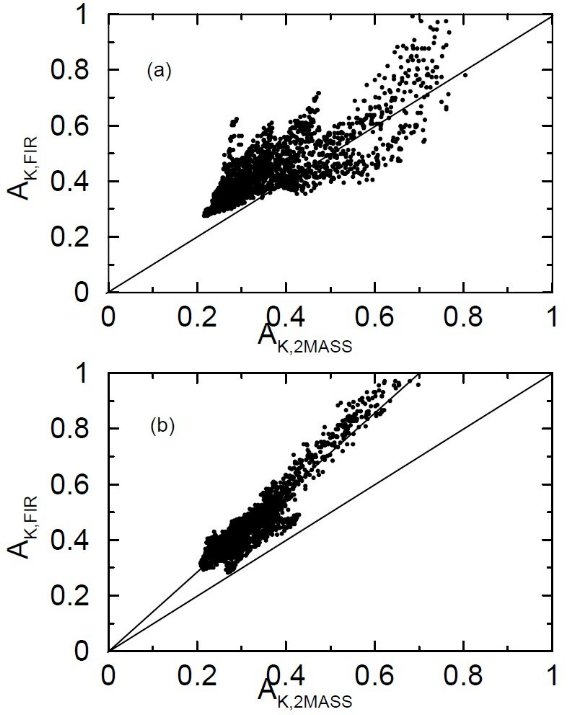図９．AK,2MASS と AK,FIR の比較。 (a) W0.2-2.1 実線：等値。(b) W359.4-3.1 上実線：AK,FIR = 1.45 AK,2MASS、下実線：等値。

向こう側のダスト　 　バルジ星の背後、向こう側の銀河面に存在するダストの効果はどうだろう？ 単純なダスト分布モデルとして、 　　　　　σ ∼ e-R/Rde-Z/Zd ここに Rd, Zd は分布のスケールである。 Rd ∼ 2.5 kpc, Zd ∼ 100 pc とし、二つの窓方向に沿って積分すると、　AK,FIR への寄与が わかる。 計算の結果、 W0.2-2.1 方向 FIR 減光の < 20 % は向こう側銀河面の 寄与であることが分かった。 W359.4-3.1 では 5 % である。従って、 違いの一部は向こう側ダストに起因するかも知れない。しかし、これで W0.2-2.1 窓の複数の枝を説明するのは難しい。 　温度効果　 　図１０には Schlegel et al 1989 のダスト温度マップを示した。 この温度マップの分解能は 1° であり、 AK,FIR の 決定には不十分である。図１０を見ると、W0.2-2.1 方向はダスト温度ピーク の近くにある。これからも、温度効果が図１０(a) の多重枝を生み出した という仮説がもっともらしく見える。 　他天体の混入効果　 　低銀緯では Schlegel et al 1989 の解析に際し銀河や星雲が除去されて いない。また、我々の解析では前景星の影響を考えていない。 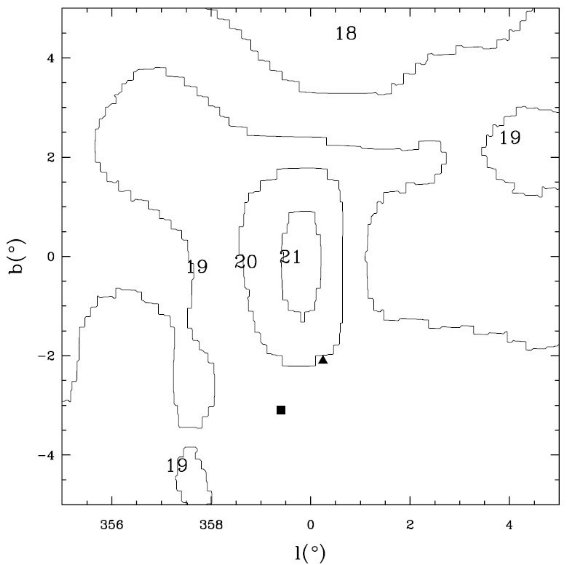図１０．Schlegel et al 1998 の銀河中心 10°×10° 温度マップ。 三角＝W0.2-2.1、 四角＝ W359.4-3.1

　４．結論