| HIIRｓ の視線速度と分光測光距離を、HI 21 cm から決まる速度と OB 星が なぞる腕の幾何構造との間を繋ぐことに用いた。星間電離水素と OB-星、 セファイドから得られる運動データは同じで、重力効果が支配的であることを 示す。 | l = [305, 333] 区間には二つの速度極大が見出される。そして、有名なペ ルセウス腕と局所腕がはっきりと分離された。HI, HIIRs, O-型星の星団が ４本の腕上に位置した。これらは ２kpc づつ離れ、ピッチ角＝ 20° で あった。 |
 図１a．Georgelin 1968 による HIIRs 励起星の分光測光距離を使った HIIRs の分布。丸の大きさは小さい方から直径 10 pc 以下、 10 - 35 pc, 35 pc 以上。 銀河系渦状腕の存在は、最初に Morgan, Sharpless, Osterbrock (1952) が HIIRs 励起星の分光測光距離を使って示した。HIIRs を選んだのは、 Baade, Mayall 1951 がアンドロメダ星雲に HIIRs のチェーンを発見したことに倣った のである。 |
 図１b．運動距離を使った時の HIIRs の分布。 彼らの研究と Sharpless (1965), の HIIRs による腕と Becker 1963, Schmidt-Kaler 1963 が O-型星、Be 星、若い星団を用いて決めた 渦状腕はよく一致し、ピッチ角 20° を与えた。図１a に同じ結果を示す。 |
 図２．ペルセウス腕における HI(電波)と HII(可視）領域の視線速度。 HI は Westerhout, Rickard 1968 より。 「21 cm 腕の可視同定」 21 cm 腕と星の腕の間の矛盾は様々に議論されてきたが未だに解決されて いない。われわれはこの問題を HIIRs 視線速度から、 「21 cm 腕の可視同定」 と言う手法で解決したい。視線に沿って見える複数の 21 cm 強度ピークの間で、 HIIR 輝線視線速度は、それらが形態上連続したチェインを指し示す時には、 連続渦状腕を選ぶ最善の方法である。 |
 図３．サジタリウス腕における HI(電波)と HII(可視）領域の視線速度。 HI は Kerr, Hindman 1967, Kerr et al. 1968 より。 l-v 図上での比較 HIIRｓ の視線速度は Courtes 1952, 1960a により最初に測られた。その後、 Courtes et al. 1968 は 150 HIIRs から 4000 本の可視視線速度を集めた。 Georgelin 1969 はその数を 6000 本まで上げた。 図２に、それらを Westerhout, Rickard 1968 と比較、図３には Kerr, Hindman 1967, Kerr 1968 と比較した。図４では Lindblad 1967 の HI データと較べた。Hα 輝線速度と HI 21 cm のピークの間には 非常に良い一致が見られる。こうして 21 cm 腕の位置を HIIRs 距離から 定めていける。 |
|
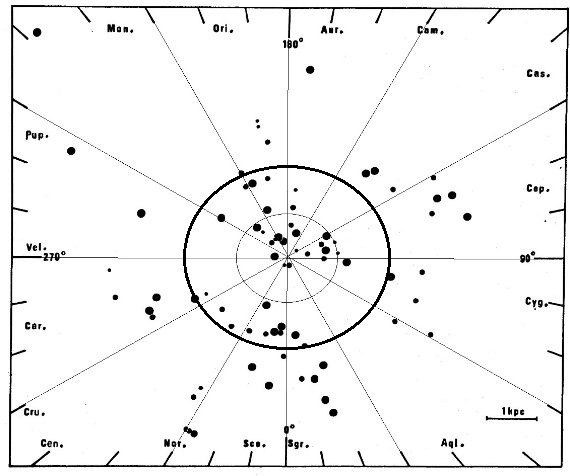
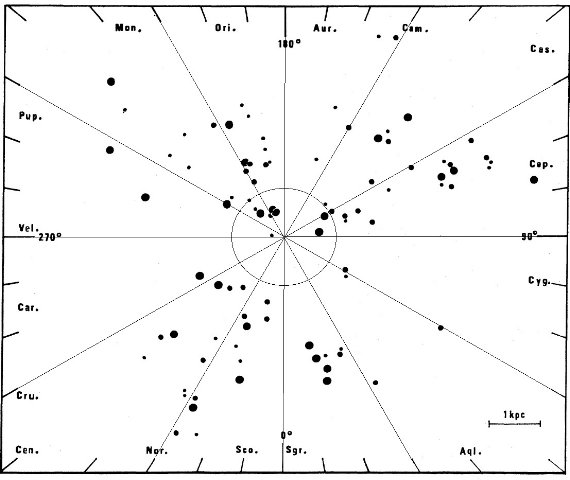
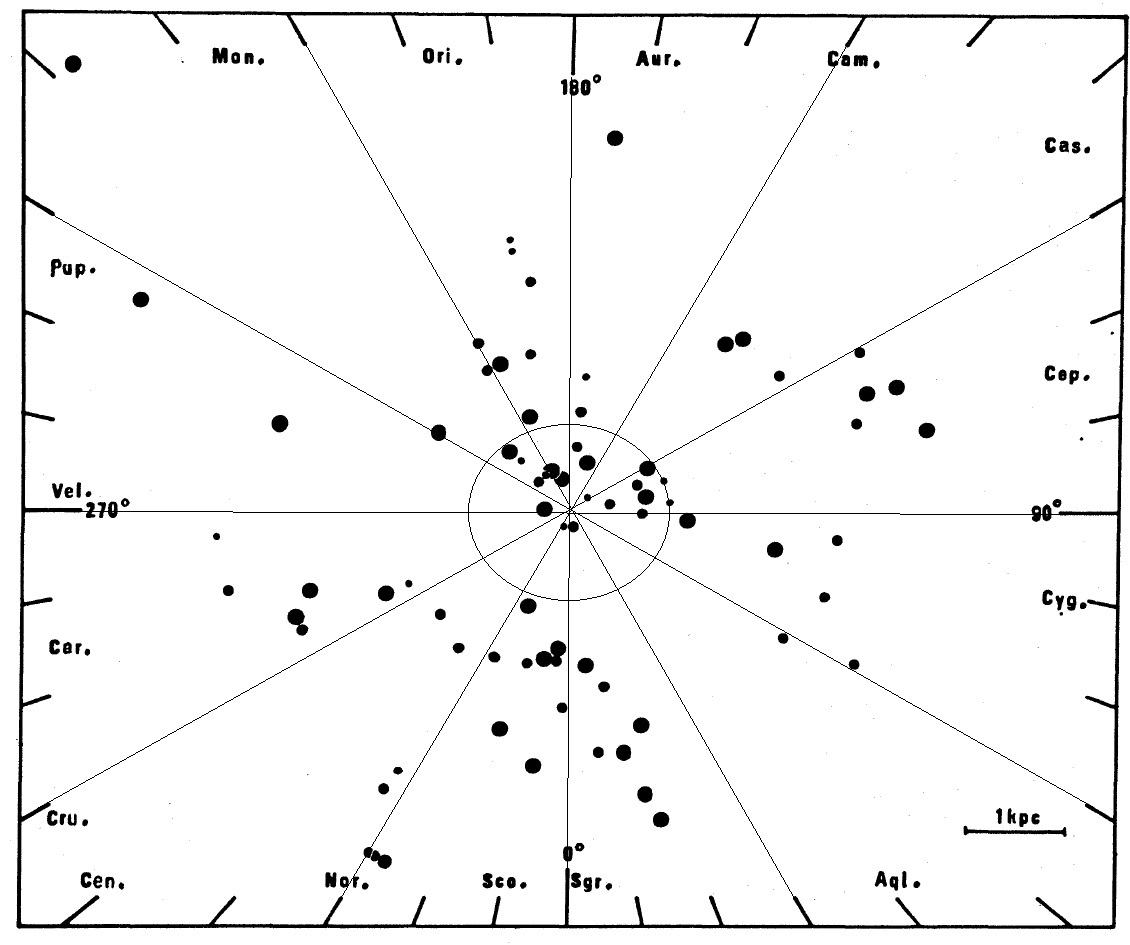
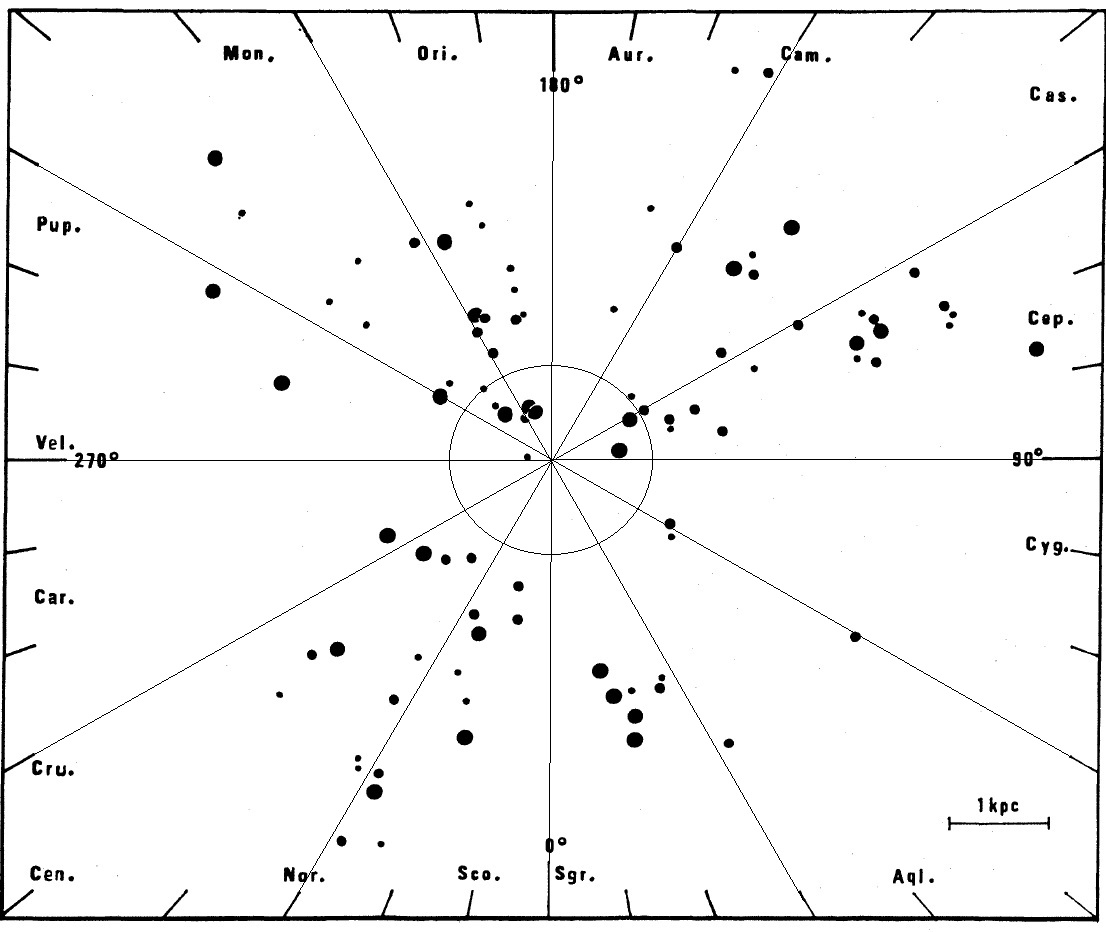
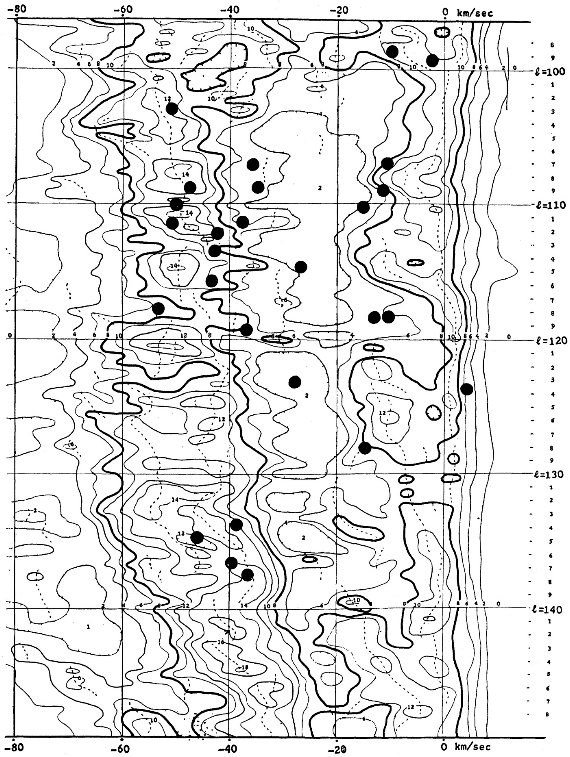
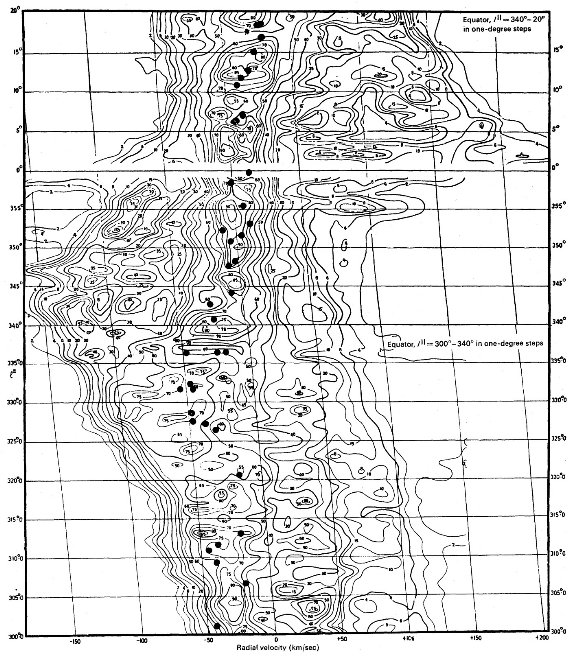
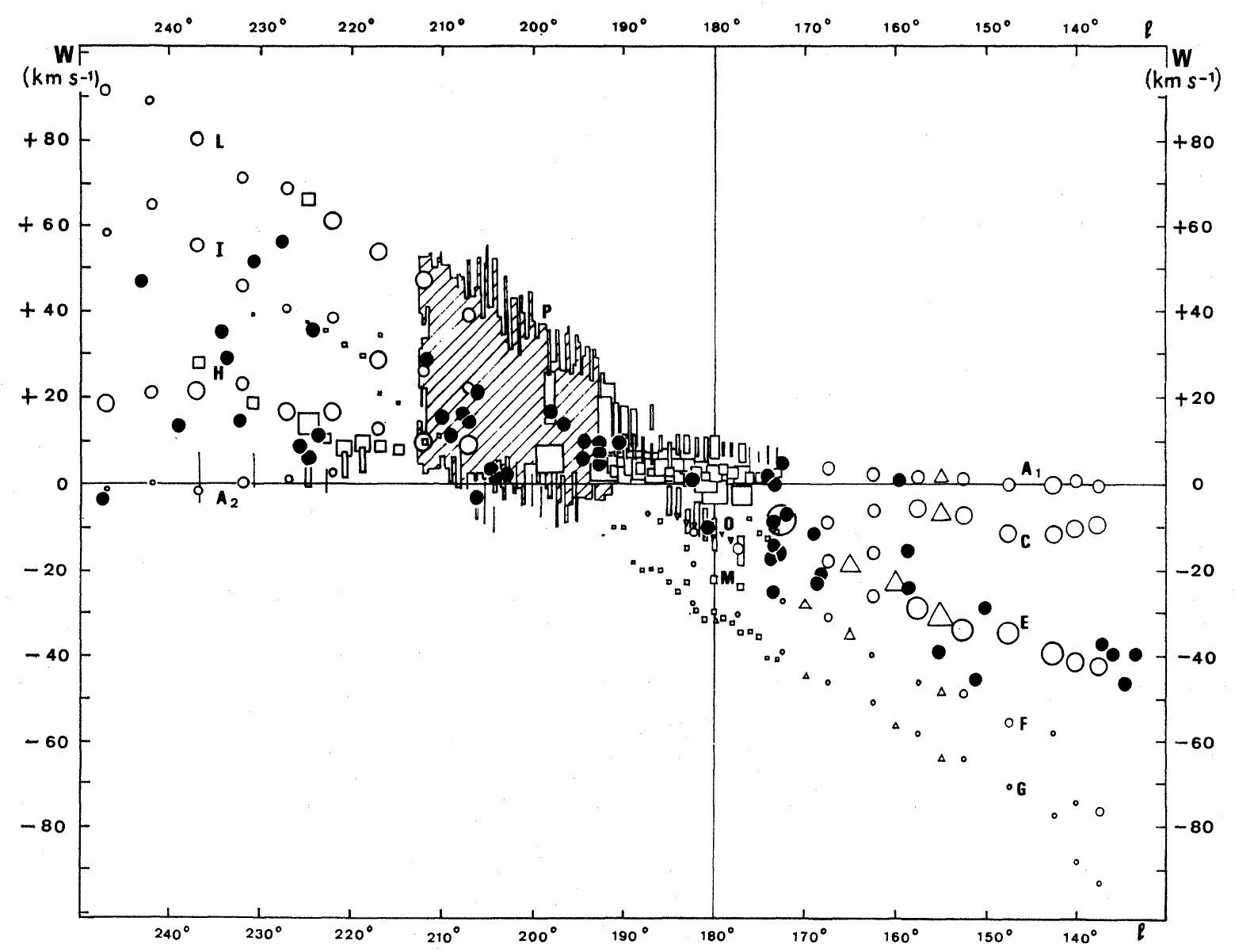
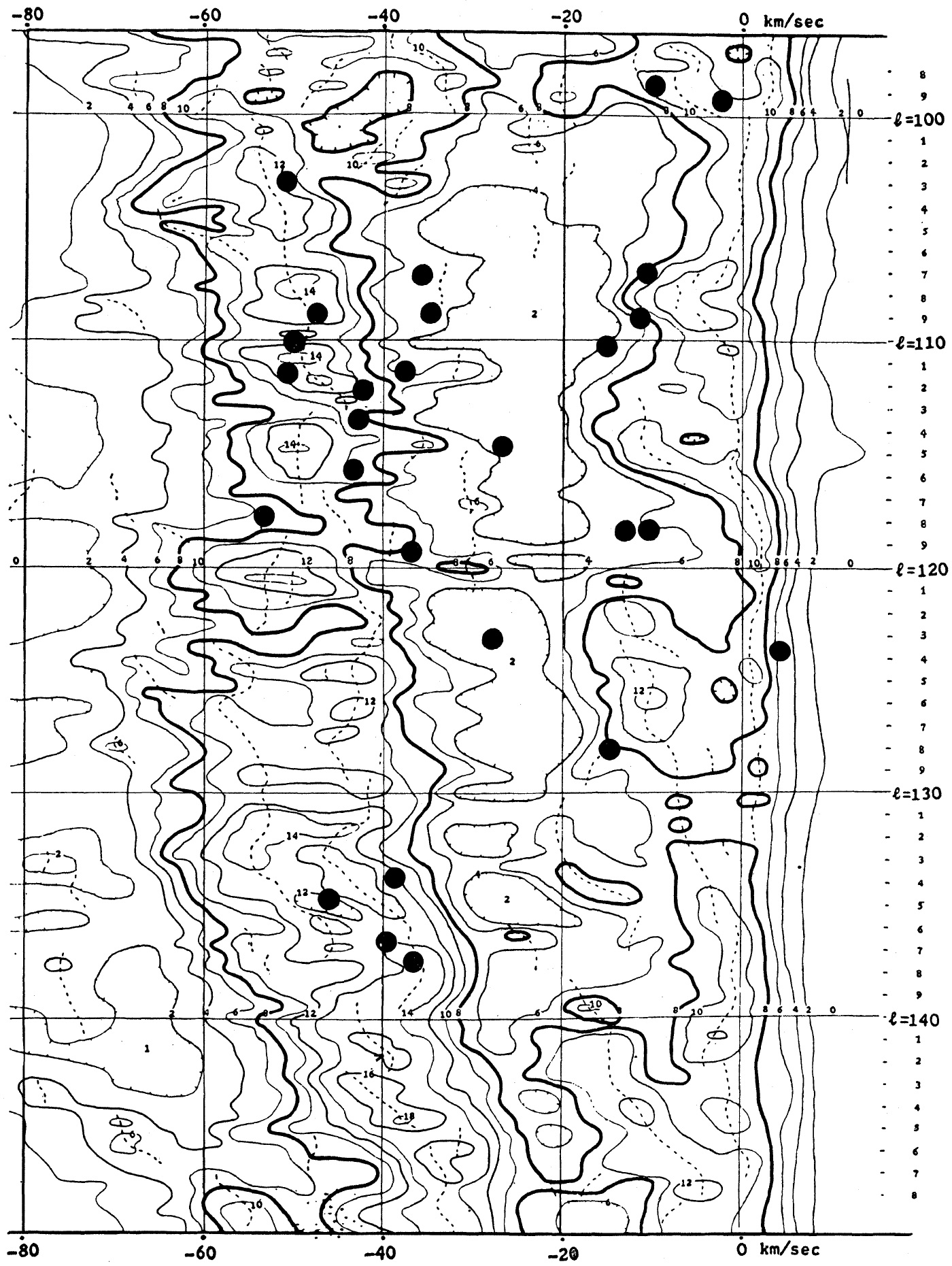
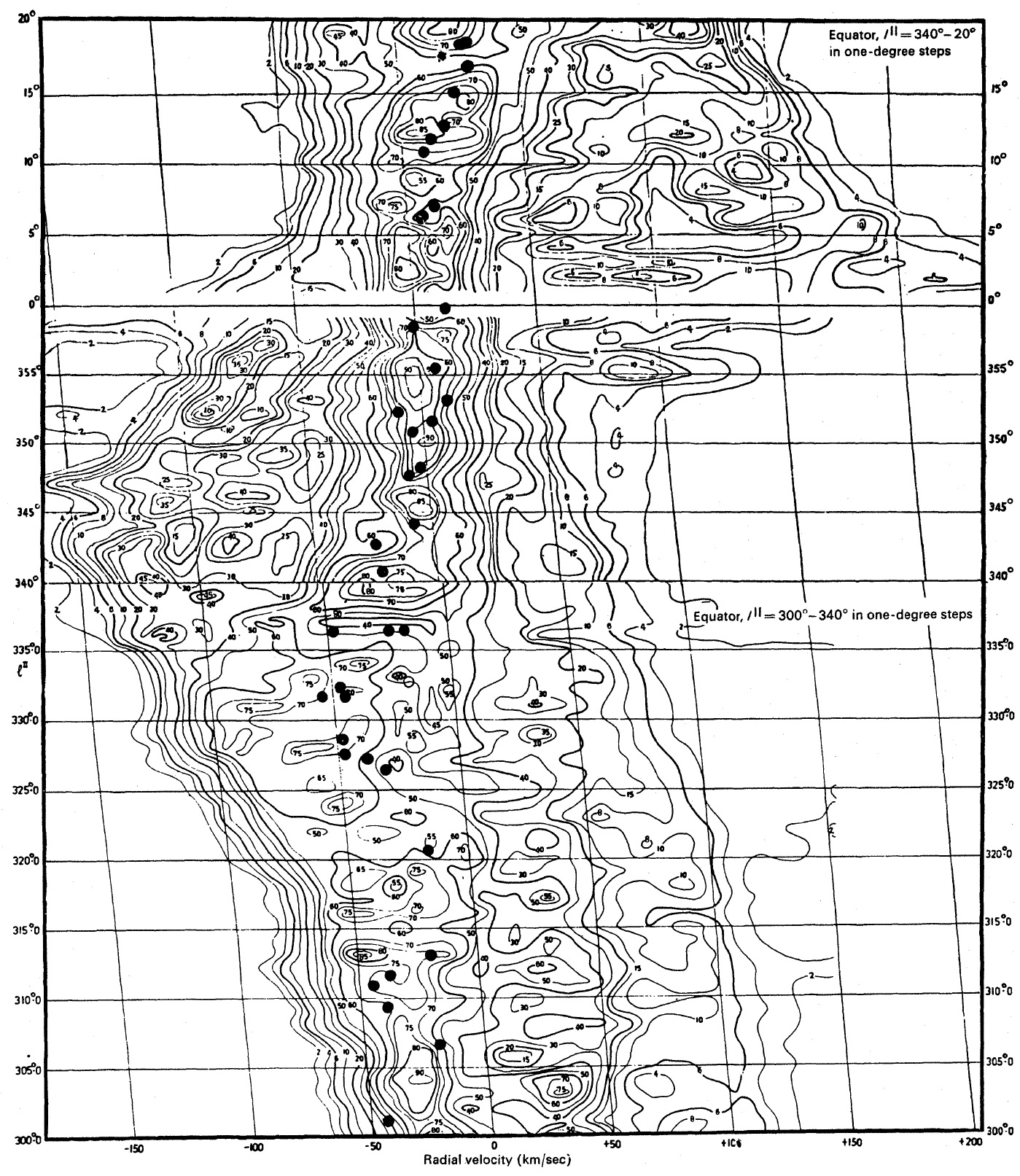
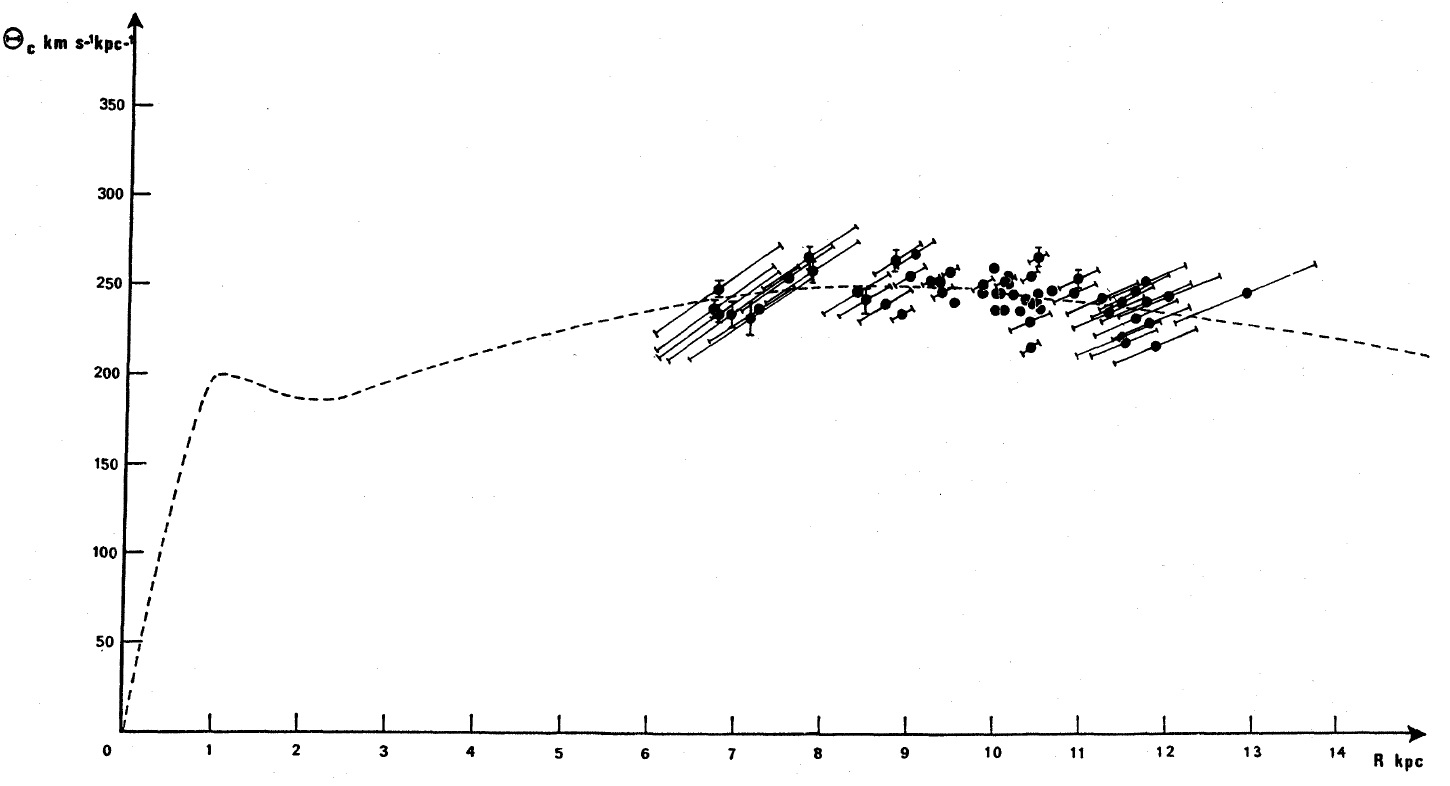
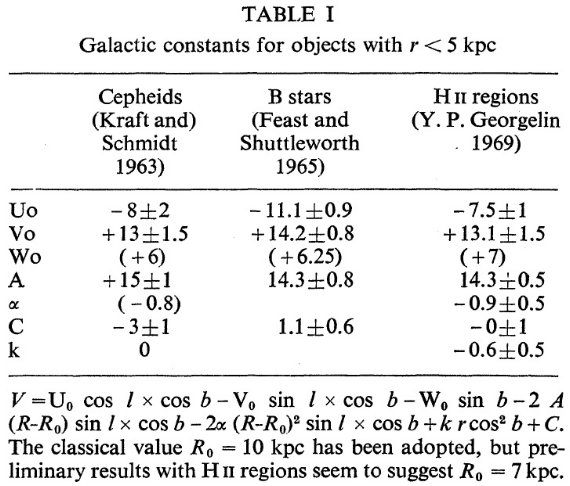
HIIRs からの回転曲線 シュミット回転曲線モデルはセファイドの視線速度と距離、及び HI 接点速度を用いて導かれた。図５に HIIRs から導いた回転曲線を示す。 シュミットモデルとの一致は明らかである。これは HIIRｓが他の種族 I 天体、セファイドや HI ガスと同じ回転速度を有することを示す。 太陽運動 (Uo, Vo, Wo), 銀河回転定数 A, 膨張定数 α, C は Kraft, Schmidt 1963 と同じ方法で計算された。表１にはその結果を Kraft, Schmidt 1963 のセファイド、 Feast, Shuttleworth 1965 の B 型星からの 結果と較べた。 ピッチ角 我々が得たピッチ角 20° は Oort et al 1958 が与えた殆ど円形の 21 cm 古典腕モデルと大きく異なる。我々は初期の 21 cm 腕モデルは データ解釈の誤りと考える。 欠損区分 21 cm 視線速度から運動距離が正しく決まるのは中心ー反中心線から 20° 以上離れる必要がある。このため、離れた腕の二つの区画を繋げるという問題 が生じる。例えば、カリーナ腕をピッチ角 0° でシグナス腕に繋げるし、 ピッチ角 25° でサジタリウス腕に繋ぐこともできる。 分光測光距離 一方、 HIIRs の分光測光距離は全銀経区間に適用可能である。特に、形態上 の連続性がカリーナ腕とサジタリウス腕の間に確立した。この連続性のお蔭で l = [0, 33] 区間の腕距離も微分回転曲線の勾配から決まる。この距離は 分光測光距離と良く合う。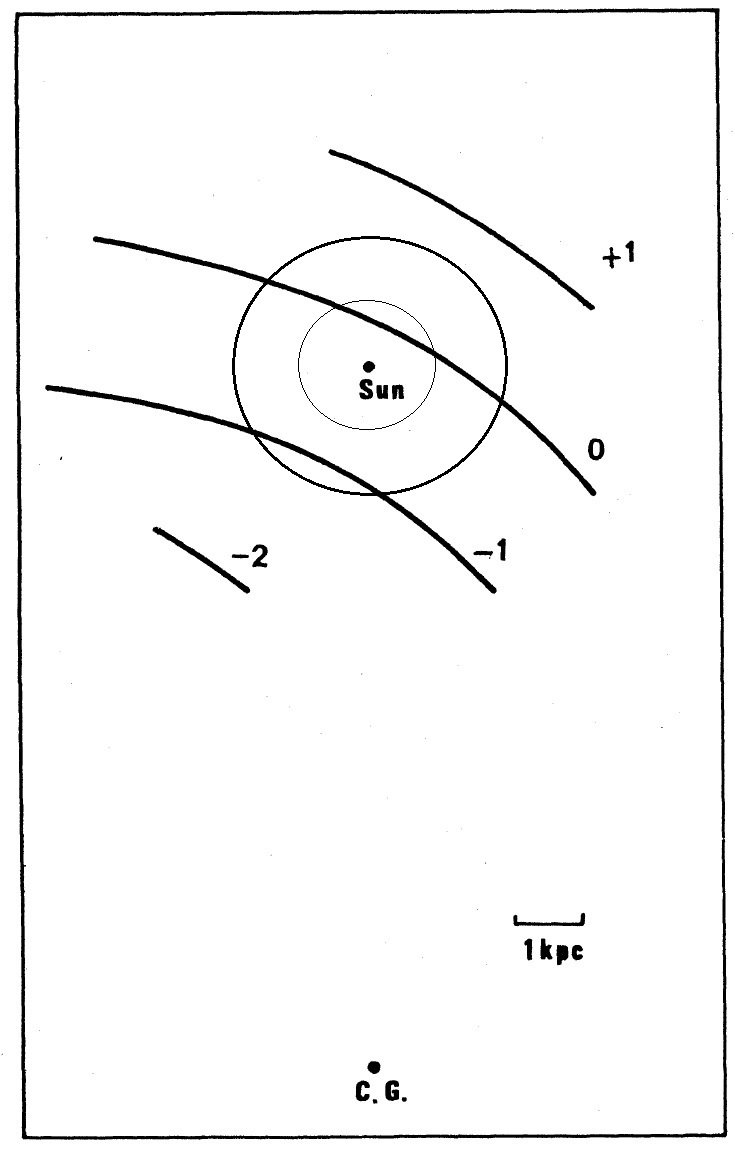 21 cm データをこのように解釈すると大きな 矛盾は解消する。 l = [305, 333] 区間では HI は r = 1 - 4 kpc に 渡る広い分布を示す。 |
 表１．r < 5 kpc 天体からの銀河系定数。 Ro = 10 kpc. しかし、HIIRs の予備結果は Ro = 7 kpc の方を支持した。 これは Oort et al. 1958 とも Kerr, Westerhout 1965 とも異なる。一方で、HIIRｓ は二つの腕の間 r = 1.5 - 3.5 kpc に明白な 分離区間を示している。 |
|
多重腕 表２と図６には４本の渦状腕を示す。HI 観測に複数の接点が現れること、 積分輝度分布、連続電波分布から銀河系が多重腕を持つことは推定されていた。 20° というピッチ角と 2 kpc という腕間距離の小ささは銀河が多重腕 構造を持つことを確かにする。 銀河系のタイプ 図７は HIIR 直径の分布が我々の銀河と M 33 （Sersic 1960）とで類似し ていることを示す。その他の色々な話から結論として 我々の銀河は SAB(rs)cd 型である。 |
 図６．渦状腕のスケッチ |
