Classification of Stellar Populations and Luminosity Classes from Accurate Proper Motions

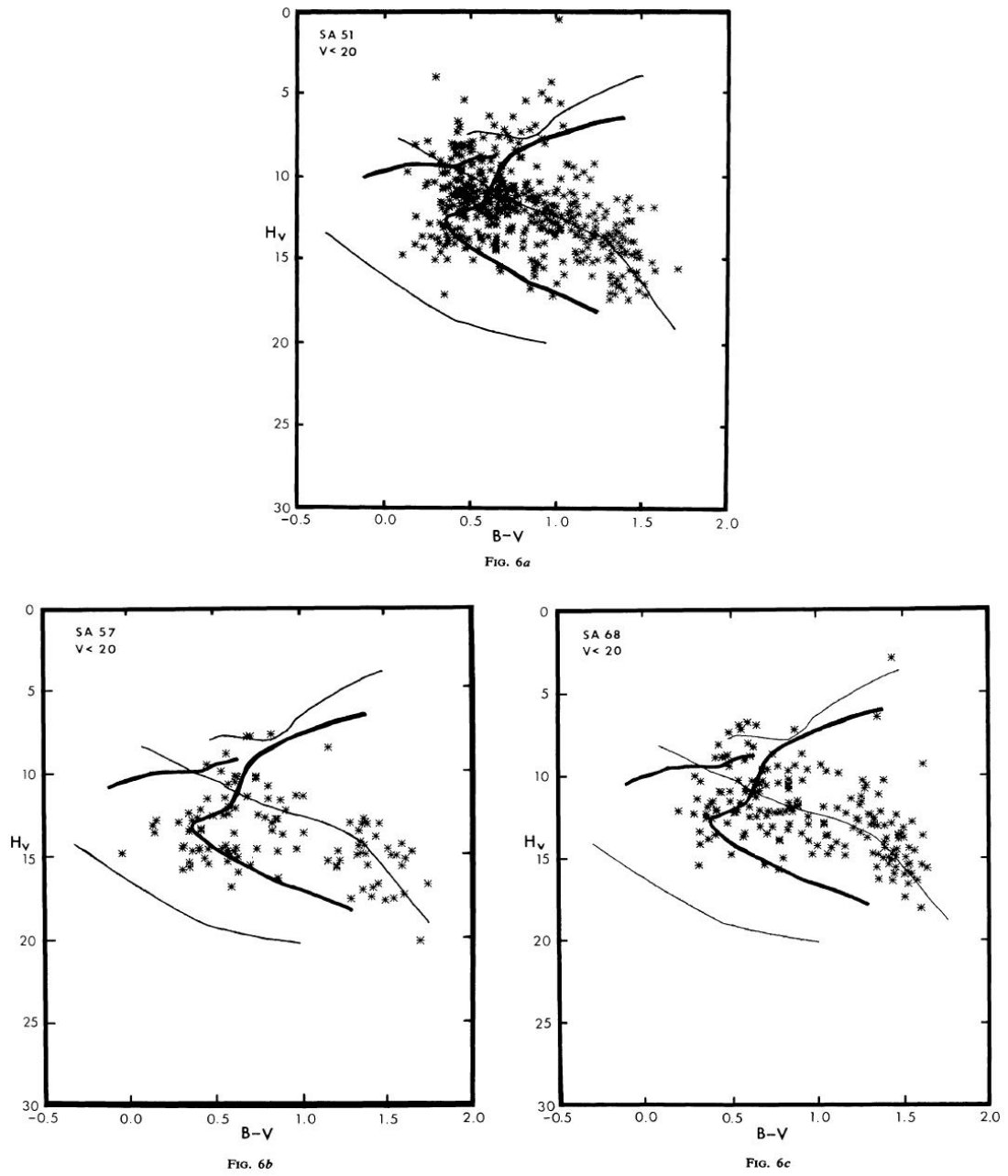
整約固有運動による分類　 　 Jones,E.M. 1972 は整約固有運動ダイアグラムを使って ブライトスターカタログの 星を分類した。さらに簡単な二成分モデルを使って、Jones はダイアグラム上に グループ毎に尾根線を引いた。この論文では Jones の仕事を次のように拡大する。 （１）直交速度 T をより正確に表現するため、速度楕円体を用いる。RA, Dec 依存性 も考慮する。 （２）Jones は種族を表現するのに単純な曲線を引いただけだった。ここでは、異なる 種族と高度クラス毎に Hv 分布を与える。こうして個々の星にそれがどの種族に 属するかのベイジアン確率を与える。 （３）固有運動の方向を示す位置角も考慮する。 　分類の結果　 こうして、Hv の分布を各種族毎に計算した。図３は B - V = 1.5 における 例を示した。HR 図では種族 I 主系列は種族 I 巨星と 10 等離れているが、 この分離は整約固有運動図でも保存される。この事実が晩期型星での光度クラス 分類の基礎となる。(Mv, B-V) 図上では種族 II 巨星は種族 I 巨星より 2 等 明るい。整約固有運動図ではその差は 2.3 等となる。図３を見ても分離はやや 弱いことが判る。 　５.e. 整約固有運動分布のモデルと観測の比較　 　図４には、図３に現れるピークをつないで作った各種族の尾根線を観測と重ねた。

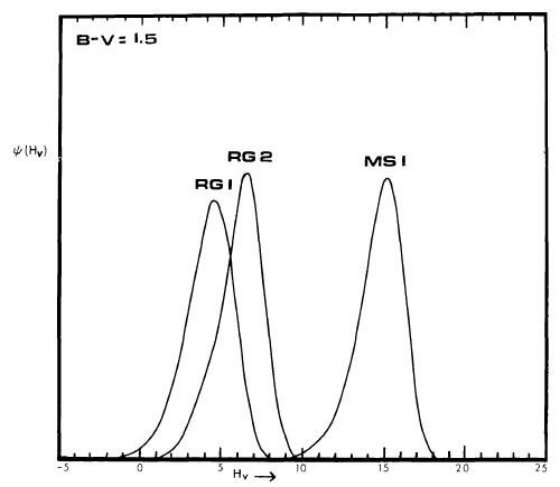
領域は SA 51 である。種族 II 系列はかなり良く観測と一致している。これは RR Lyr 星の速度分散と M92 の色等級図が実際にマッチしていることを示す。 モデルと観測が最もずれるのは種族 I 主系列線が観測の 1.2 等上に引かれた ことである。同じ傾向は SA 57, SA 68 でも見られる。 その解決のため、 速度分散の変化とか、色等級関係の変化とかいろいろ考えて合わせている。 しかし、ちょっと発散。 　図３．B - V = 1.5 における　Hv 分布。