The Determination of Ultraviolet Extinction from the Optical and Near-Infrared


Cardelli, Clayton, Mathis
2008 ApJ 329, L33 - L36



　アブストラクト

　可視／近赤外減光と紫外減光との相関　
　Fitzpatrick, Massa 1986, 1988 の UV 減光が得られた星のうち、UBVRIJHKL 測光データを調べた。A(λ)/Av で考えたとき、可視／近赤外減光と紫外 減光との間によい相関が存在することが分かった。特に、 R = Av/E(B-V) は Fitzpatrick,Massa の紫外減光曲線の線形紫外背景減光部と相関が強い。

R から紫外減光を推定する　
　R から紫外減光強度を推定できることを意味する。R から紫外減光則を導く 解析表式を求めた。この式で、R = 3.2 の場合の曲線は Seaton 1979, Savage, Mathis 1979 の平均減光曲線と極めてよく一致する。この減光則は希薄星間空間に 対応する。

　解析表式の方がより正確　
　これまで平均減光則を全ての方向に適用したり、バンプに「アイロンかけ」 したりしてきたが、3.1 < R < 3.5 では解析表式の方がより正確な 減光則を与える。

　1.イントロ　

減光則のパラメタ―表示　
　Fitzpatrick, Massa 1986, Fitzpatrick, Massa 1988 は観測された紫外減光曲線のある成分、 例えばバンプの中央波長 λo や 幅 γ が星間空間の環境 条件、温度、密度、輻射場などと関係することを見出した。 λo はわずか、±17 A、の変動しか示さないが、 γ は濃くて 暗い雲では大きくなるようだ。特に HD 62542 と HD 29647 方向では λo や 幅 γ が Fitzpatrick, Massa 1986 サンプルの範囲外 にはみ出し、極端な環境変性の例を与えている。

　R 変化は長波長側の 減光には影響しない　
　可視、近赤外減光で標準減光則からの偏差が見られることは以前から知ら れていた。特に高密度空間方向では、R = Av/E(B-V) が大きくなり、ダスト 粒径が大きくなることがその原因であろうと想像されていた。 Clayton, Mathis 1988, Cardelli,Clayton,Mathis 1989 は R 変化は λ < 0.6 μm の減光を伴うが、長波長側の 減光には影響しないことを見出した。
( 単純な言い方では λ = 0.6 μm で短波長側減光曲線がカクッカクッと折れ曲がること？)
この変化は R が増加した時に可視、近赤外の減光が上向きに反ることを 意味する。

　紫外域と可視/近赤外域の減光則の関係　
　紫外域と可視/近赤外域の減光則の関係は殆ど研究がなかった。しかし、
（１）E(B-V) で規格化された UV 減光の解釈は、E(B-V) 自体が UV 減光 に関係するので過ちやすい。
（２）可視と紫外の減光の相関により、一方の観測しかない時でももう片方の 減光を予測できる。
　ので、重要なテーマである。


　２．データと解析方法　

　サンプル星　
　サンプル星は Fitzpatrick, Massa 1988 が UV 減光を測った 45 星から採った。 文献から UBVRIJHKL データを集めた。少なくとも五バンド以上という条件で ２０星が得られた。内部整合性のためスペクトル型は全て Fitzpatrick, Massa 1988 から採った。固有カラーには Johnson 1966 の値を使用した。FitzGerald 1966 Koornneef 1983 のカラーとの差は色超過の大きさに比べると小さくて結果には 影響しないことが分かった。Johnson 1966 時代には H バンドは設定されて いなかった。本論文では

　　　　　(V-H)o = 0.20(V-J)o + 0.80(V-K)o

という内挿式で代用する。Of 型星は H バンドより長波長側で赤外超過を 示すが、サンプルから除外しなかった。それについては後に述べる。

　 R 決定の第１の方法　
　色超過 E(λ - V) を x = 1/λ(μm) の関数としてプロットする。 Rieke, Lebofsky 1985 減光曲線をガイドに、この超過曲線を目分量で x = 0 まで外挿する。 		　第２の方法　
　Clayton, Mathis 1988 の解析的方法を適用する。簡単に言うと、 V(0.55μm) とそれより長波長側では全ての星で減光則は Rieke-Lebofsky 型で あり、変異はそれより短波長側で起こると仮定する。λ > V の色 超過 E(λ-V) を Av を唯一のパラメタ―として Rieke-Lebofsky 型で フィットする。

　二つの比較　
　二つの方法から得られた Av は 0.1 mag の範囲で一致した。例外は θ 1 Ori C と Herschel 36 で、どちらも J バンドの先で減光曲線 が下向きに傾く。この効果は HIIR 内の温かいダストからの放射の混入のため と考えられる。

　A(λ)/A(V) の決定　
　Fitzpatrick, Massa 1988 の表１には彼らの４つの UV 減光曲線式係数が載 せてある。その式を用いて我々は E(λ-V)/E(B-V) を数値的に求めた。 可視・近赤外測光から求めた A(V) を使って、我々は

　　　　　A(λ)/A(V) = E(λ-V)/A(V) +1

を決める。


　３．結果　

　図１の説明　
　図１には二つの方向での A(λ)/A(R) を x = 1/λ に対して示す。 紫外減光強度が B-V 間の勾配と強い相関を有することが明らかである。図上 この勾配は 1/R = E(B-V)/A(V) と関係する。 Fitzpatrick, Massa 1988 は減光曲線から数学的に背景線形成分を分離した。図１ではこの線形成分を破線 で示した。この線形部分は可視減光曲線の延長であることに注意せよ。
(そうは見えないけど。 )

　図２の説明　
　図２の上プロットは A(22)/A(V) である。ここに A(22)は 2175 A ピーク での減光を表す。シンボルは視線方向の環境（黒＝希薄星間空間。白＝濃い 空間。半黒＝星形成域。バツ＝ HD 29647）を示す。図から A(22)/A(V) と 1/R の間にきれいな線形関係が成立することが分かる。
　図２下側プロットは Alin(22)/A(V) を示す。 Alin(22) = Fitzpatrick,Massa 1988 モデルの紫外背景減光の線形フィット。


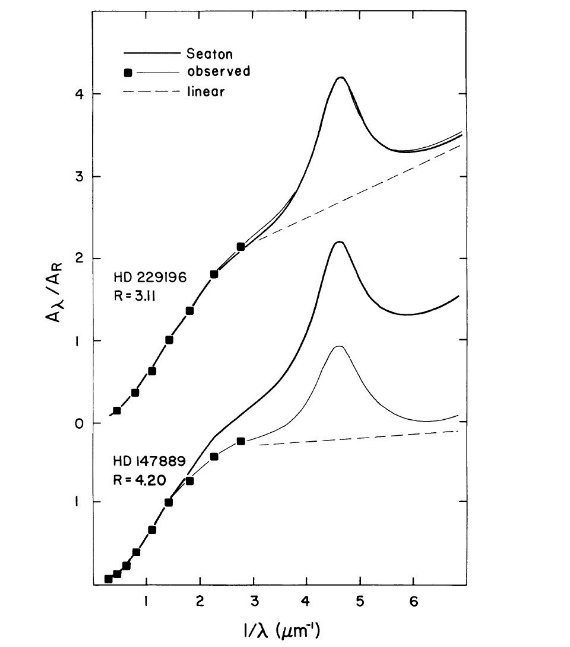
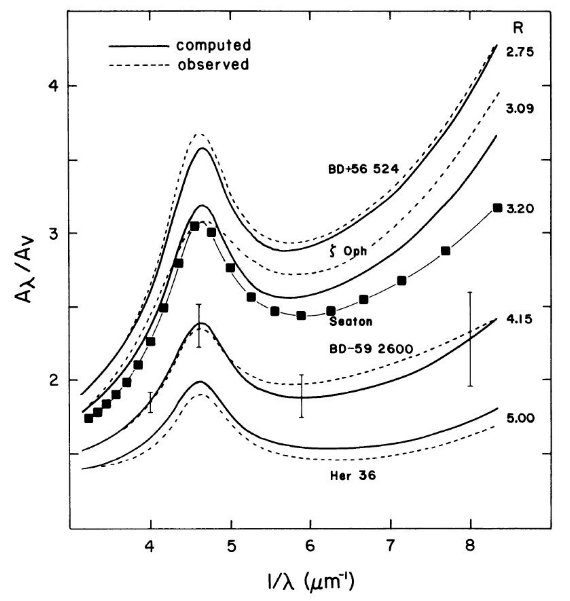
図１．AR で規格化した減光曲線。黒四角＋細線は二つの星の 減光曲線。太線＝Seaton 1979 の平均星間空間減光曲線。破線＝ Fitzpatrick,Massa 1988 表式での背景線形紫外減光。 R が大きくなると、 可視・赤外の減光が turn over し、それが UV に carried over されていく。 		　図２の線形関係の解釈　
　我々はこの線形関係は、可視・近赤外側での勾配の変化が紫外側に背景 紫外減光として持ち越されてきた結果、と解釈する。上のプロットの分散 が大きいのはコブの強さが様々なためであろう。しかし、Fitzpatrick,Masaa 1988 では コブ/A(V) も 1/R と相関していることを注意しておく。この 相関の意味は Cardelli,Clayton,Mathis 1989 で論じる。

　線形関係の拡張　
　図２で見た、A(λ)/A(V) と 1/R の線形関係は 0.12 < λ < 0.30 μm の全波長で成立する。従って、純粋に地上観測のみで R を 定めれば 紫外減光に対してかなりの精度で予測可能である。つまり、R の 値毎に平均減光曲線が存在する。








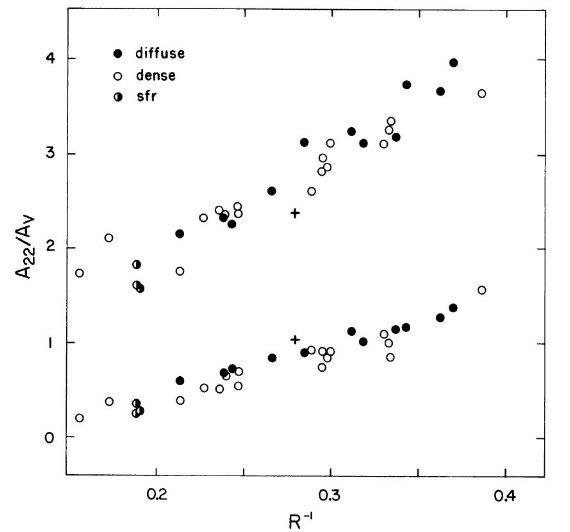
図２．上のプロット：　A(22)/Av. A(22)は 2175 A ピークでの減光。
下のプロット：　A(22)/A(線形部). A(線形部)は Fitzpatrick, Massa 1988 モデルの紫外背景減光の線形フィット。見やすさのため１だけ下げてある。
黒＝希薄星間空間。白＝濃い空間。半黒＝星形成域。バツ＝ HD 29647

　線形関係から得た減光曲線の表示
　A(λ)/A(V) と 1/R の関係を一次式

　　　　　　⟨A(λ)/A(V)⟩ = a(x) + b(x)/R

でフィットした。図３にはこうして計算した ⟨A(λ)/A(V)⟩ をサンプル中の４星の方向について x = 1/λ の関数として 示した。同時に４星の観測値および、フィット式と観測値との差の rms も エラーバーとして R = 4.15 曲線上に示した。標準減光曲線も示した。

　R = 3.2 から離れると標準減光則が適用 できない　
　Meyer, Savage 1981, Massa 1987 は特異減光の方向で標準減光則を適用 することに強く警告していた。図から分かるように、 R = 3.2 から離れた 場合に標準減光則が適用できないことは図からもよく理解できる。

　a(x) と b(x)　
　a(x) と b(x) を解析表示すると以下のようである。

　a(x)=1.802-0.316x-0.104/[(x-4.67)2+0.341]+Fa(x)

　b(x)=-3.090+1.825x+1.264/[(x-4.62)2+0.263]+Fb(x)

x≥5.9 では、
　Fa(x)=-0.04473(x-5.9)2-0.009779(x-5.9)3

　Fb(x)=0.2130(x-5.9)2+0.1207(x-5.9)3

x<5.9 では、
　Fa(x)=Fb(x)=0

　減光則が R のみで決まる物理的理由 　
　以上の単純な線形関係はおそらくグレインサイズの分布に関係する。 R の大きな、一般には濃い星間雲中、では大きな粒子が多いのであろう。 おそらくグレインのサイズ分布はストカスティックな過程で成立し、サイズ 分布はプロセッシングの度合いを表すパラメタ―が一つで決まり、これが 減光則が一つのパラメタ― R のみで表される根底にあるのだと思われる。

　コブと遠紫外　
　2175 A バンプと遠紫外もやや弱い相関はあるが、それらは可視減光に 関与するグレイン種族とは独立に振る舞うように見える。それでも、一般 的な傾向は紫外の線形成分には強い相関として表れている。

図３．A(λ)/A(V)のモデル曲線と観測曲線。一致の良さが わかる。Seaton 1979 の平均減光曲線も示した。R = 3.2 に対する モデル曲線は x < 6.5 で標準曲線と殆ど区別できないほどよく一致する。

　例外の星　
一つの例は HD 29647 である。この星は コブの位置が大きくずれ、弱く幅広。遠紫外では急勾配。図２ではこの星を プラス印で表した。図２下の A22/A(V) は他データとよく適合する。 もう一つは LMC である。どちらも背景線形減光は正常らしいが、コブと遠紫外 の立ち上がりがおかしい。
　Fitzpatrick,Massa 1988 サンプル中の７個は使用しなかった。これらの 星も輝線の影響等を処理すれば将来は使える。