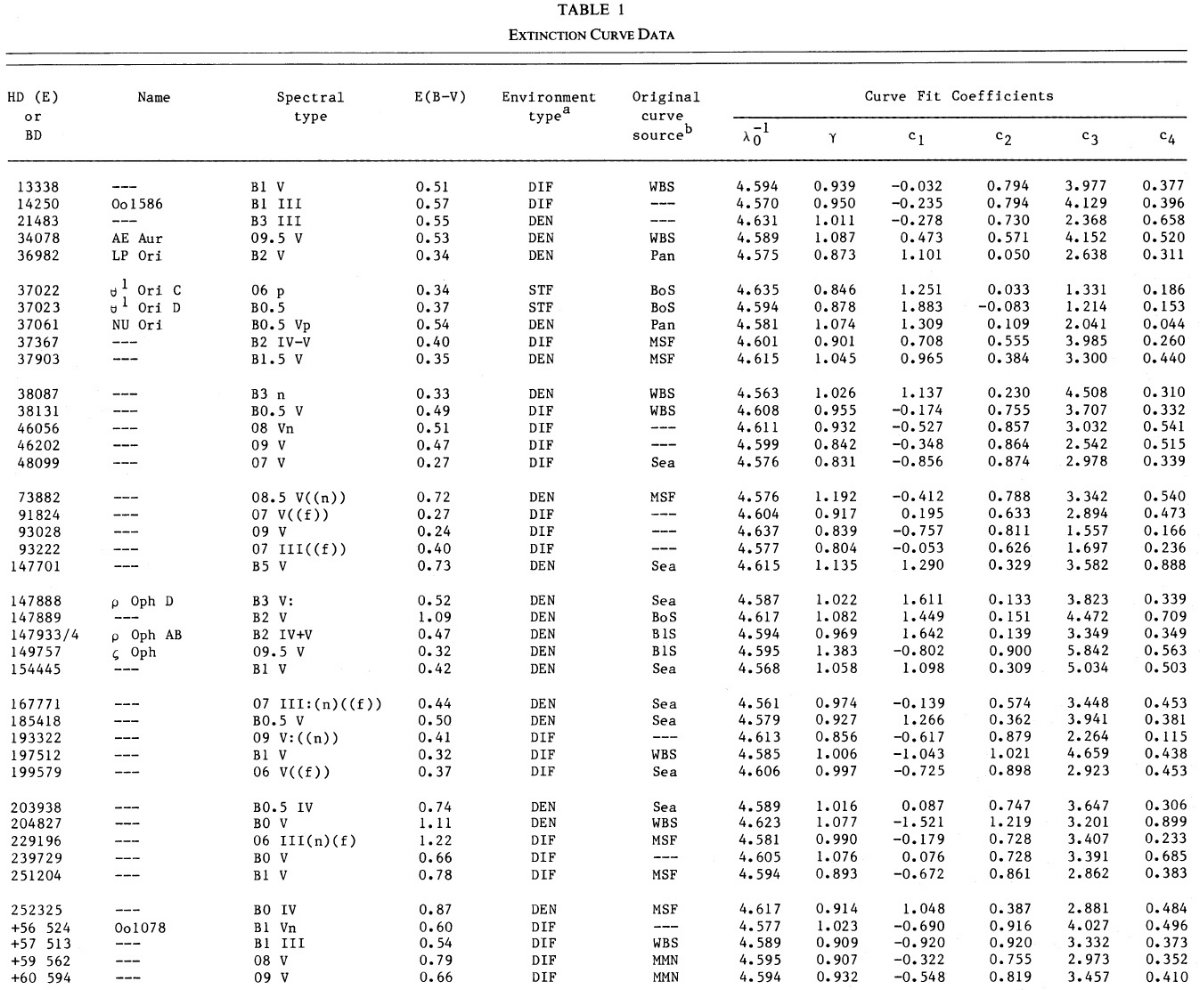
アブストラクト紫外減光曲線を3成分モデル化OB 星 45 個の IUE データを用い、λ < 1700 A での星間減光を 調べた。IUE 減光は(1)ローレンツ型 2175 A コブ、(2)FUV 反りかえった 減光、(3)背景の線形型減光の和で表される。線形成分のパラメタ―、 勾配と切片、は強く相関しており、その結果、わずか5個のパラメタ―で 紫外減光をフィットできることが分かった。それらは、コブの3つ、線形部 が一つ、最後の一つが反り返り成分強度である。 反り返り成分は共鳴吸収のテールか ? 反り返り成分は同じ形をして いることが分かった。これは、この成分がサイズ分布などの効果で生まれた 形でなくあるダスト成分の物理性質を反映しているからと考えられる。 恐らく極端紫外部での共鳴吸収のテールであろう。 |
1.イントロFitzpatrick, Massa 1886 のまとめドルーデプロファイルが IUE で観測された 2175 A コブによくフィット することを示した。コブの FWHM = 360 - 600 A, λo = 2174.4 ± 17 A であった。コブの幅は高密度空間では大きく、希薄空間では狭い。 最近星形成が起きた領域ではさらに狭い。 この論文では遠紫外減光を扱う この論文では遠紫外減光を扱う。特にそれとコブとの相関を調べる。IUE 減光曲線 は6つのパラメタ―を含む単純な関数でフィットできることが分かった。 |

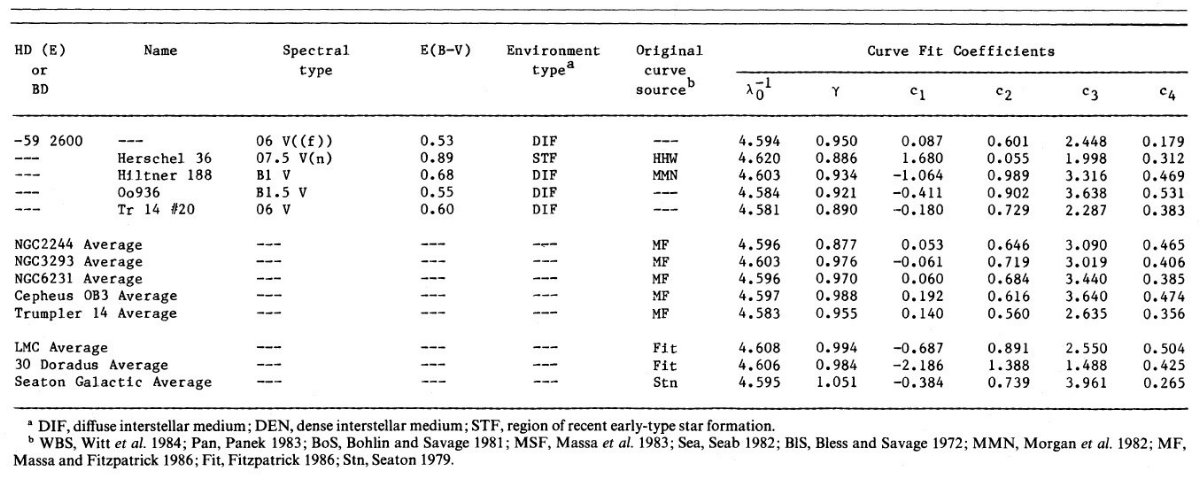
|
サンプル星 サンプルは IUE 低分散モードで取った 45 星の減光曲線である。詳しい情報 は Fitzpatrick,Massa 1988 論文IIIに載る予定である。減光曲線の形成には Fitzpatrick,Massa 1986 に提案したペア法に依った。標準星についても 論文 III に載せた。Lyα 吸収の補正は行ったがそれでも 1200 - 1230 A は S/N が悪くて使用不可能であった。 |
HI コラム密度 HI コラム密度の導出は Lyα ウイングにプロファイルフィットする (Bohlin 1975) ことで行った。この方法で得たコラム密度はコペルニクス や IUE 高分散スペクトルからの結果 (±25% 精度)と比べ ±40% で一致した。HI コラム密度は論文 III に載せる。 |
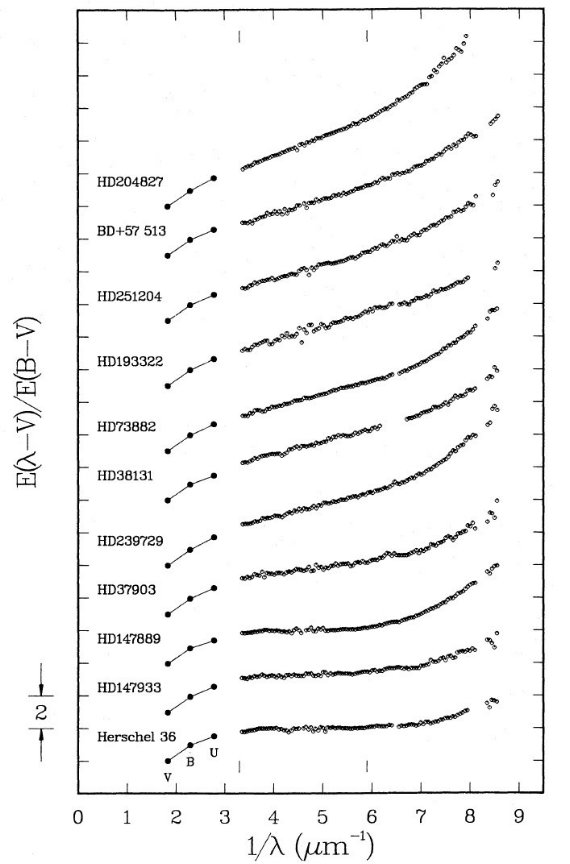 図1.コブを取った後、つまりドルーデプロファイルを λ-1 = 1.8 -8.5 ($lambda; = 0.12 - 0.55 μm) で差し引いた残り。ドローデ プロファイルのフィットには 3.5 - 5.9 μm-1 部分(図中 縦線)が用いられた。黒丸=UBV 測光。白丸=IUE分光測光(0.05μm -1 ビン)。 |
3.a. λ < 1700 A での減光曲線図1=ドルーデプロファイルを差し引いた残り図1には、コブを取った後、つまりドルーデプロファイルを $lambda;-1 = 1.8 -8.5 ($lambda; = 0.12 - 0.55 μm) で差し引いた残りを示す。ドローデ プロファイルのフィットには 3.5 - 5.9 μm-1 部分(図中 縦線)が用いられた。黒丸=UBV 測光。白丸=IUE分光測光(0.05μm -1 ビン)。残差部分は滑らかでかなり線形性が良い。 図2=反り返り成分 残差曲線には 7 μm-1 の先で直線からのずれが現れる。FUV のデータが良質の 18 星について、残差から ドルーデプロファイルと直線成分を差し引いた残り、18星分 の平均にスケールを合わせて重ねた図を図2a に示す。驚くべきことに、 18 星の残差部分は規格化すると非常によく重なる。つまり、反り返り部分 は同じ関数でフィットできるのである。その近似式は F(λ-1) = 0.5392(λ-1-5.9) 2 + 0.0564(λ-1-5.9)3 (λ-1>5.9) = 0 (λ-1<5.9) 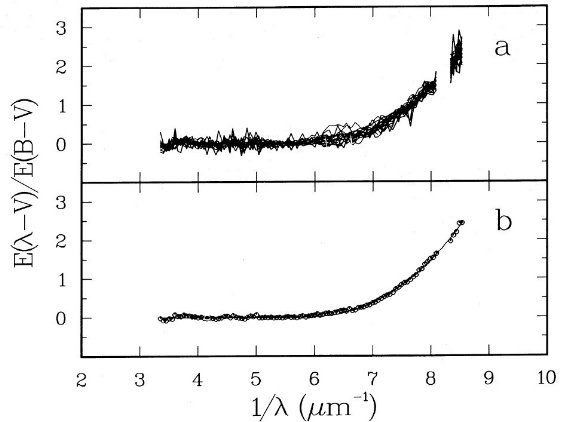 図2.(a). ドルーデプロファイルと直線成分を差し引いた残り。18星 の残り部分の平均にスケールを合わせて重ねた。 (b). 白丸=18星の平均。実線=多項式フィット。 |
3.b. 紫外減光曲線のパラメタ―化紫外減光の3成分近似式これまでの結果から、IUE 減光曲線はドルーデのコブ+背景線形減光+ FUV 反り返り で表現できることが分かった。式で表すと
ここに x = λ-1、D はドルーデプロファイル、
、F は3.a. で定義した線形背景減光である。上の式には6つの パラメタ―が含まれている。45 のサンプル星に対するフィットの結果は表1 に示した。 コブ 本論文でのコブの扱いはいくつかの点で論文 I と異なる。 (1)ドルーデプロファイルのフィット波長範囲を広げた。 (2)線形背景減光をコブ領域に限定せず、 FUV にまで広げた。 その結果、コブのパラメタ―は論文 I とは少し変わった。大部分の星では差 は測定誤差程度であるが、コブが浅い星のいくつか、ζ Oph, HD 93028, NU Ori, HD 147889 では差が大きくなった。 |
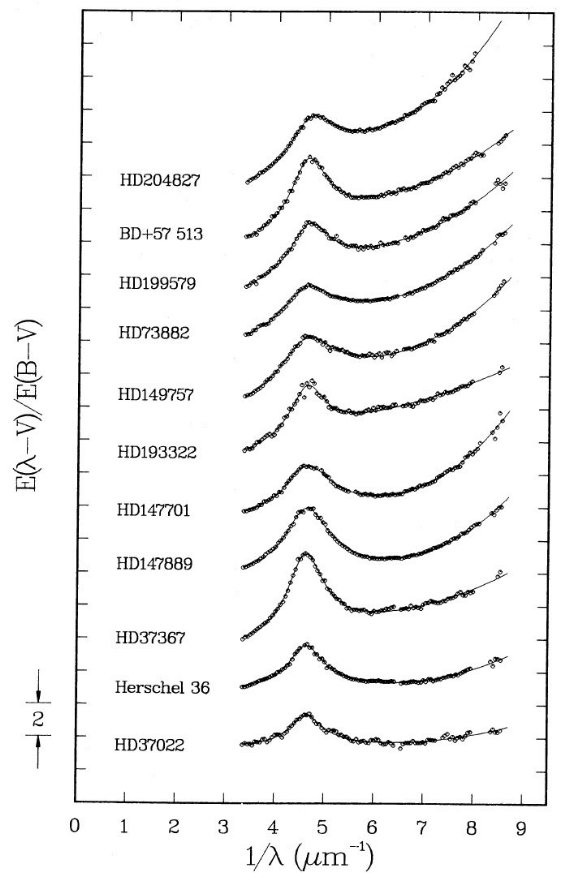 図3.サンプル星11個へのパラメタ―フィットの例。 |
4.a. パラメタ―・パラメタ―相関線形成分パラメタ―間の相関図4には c1 と c2 の相関を示した。c1 = 線形背景減光切片、 c2 = 線形背景減光勾配である。小丸: オリオン星雲の星、HD36982, HD 37023, HD 37061、は星雲放射光の混入が疑わ れるので破線=フィットから除いた。 フィットの結果は c1 = -3.00 c2 + 2.04 である。この結果を減光線形成分の式に代入すると、
となる。この式は (λ-1, E(λ-V)/E(B-V)) が (V, 0), (B, 1), (3.00, 2.04) を通り、その先では (3.00, 2.04) から c2 勾配で放射状に広がることを述べている。 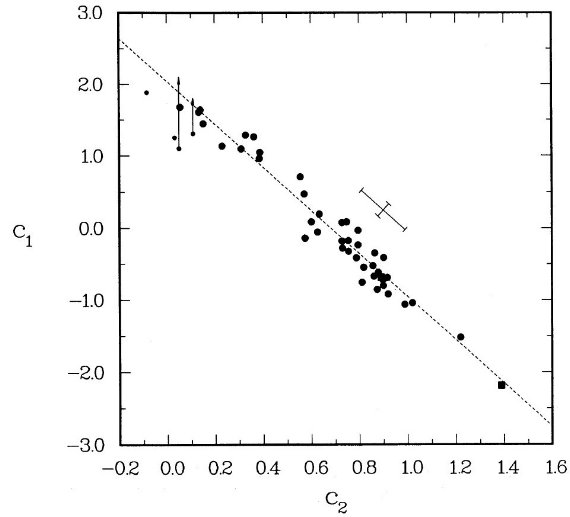 図4. c1 - c2 相関。c1 = 線形背景減光切片。 c2 = 線形背景減光勾配。小丸:オリオン星雲の星、HD36982, HD 37023, HD 37061、は星雲放射光の混入が疑われるので破線=フィットから除 いた。 |
コブパラメタ―間の相関 コブ中心波長の変化は小さいので相関は調べない。図5には c4 = FUV 反り返り強度と c3 = コブ強度との 相関をプロットした。コブ強度は E(B-V) で規格化されていることを 注意する。この図で重要な点は、左下から右上へ進むにつれ、点の分布が 次第に広がり、かつコブ幅 γ が広がっていくことである。 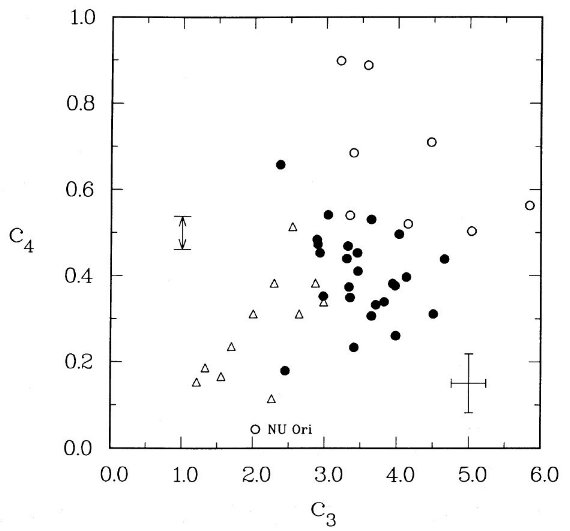 図5. c4 - c3 相関。c4 = FUV 反り返り 強度。c3 = コブ強度。 三角: γ < 0.9、 黒丸:0.9 < γ < 1.05、白丸: 1.05 < γ。 |
|
FUV 反り返り強度とコブの巾の相関 図6の(上)には c4 = FUV 反り返り強度と γ = コブの巾 との良い相関が示されている。ただし、 c4 は E(B-V) で規格化 されているのに γ は規格化に無関係なので、解釈は単純でない。 図6の(下)には c3 = コブ強度と γ = コブの巾 との相関が示されている。解釈は第5章で行う。 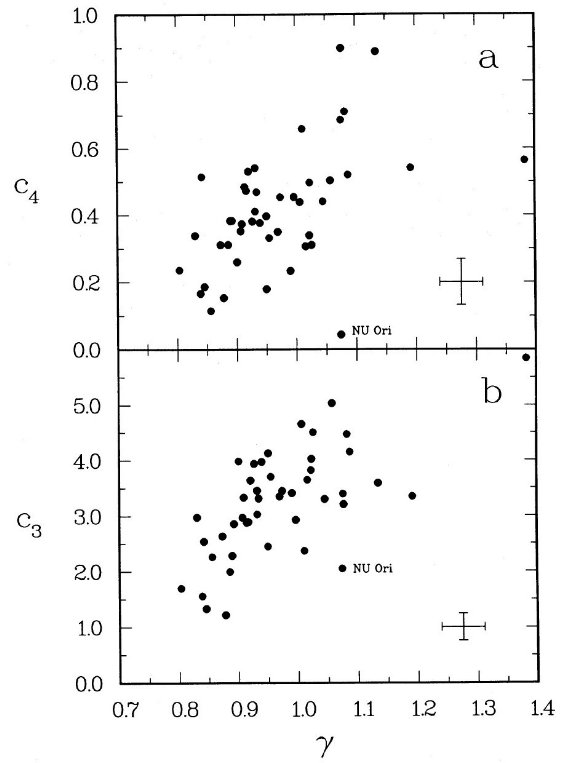 図6.(上):c4 - γ 相関。c4 = FUV 反り返り 強度。γ = コブの巾。 (下):c3 - γ 相関。c3 = コブ強度。 |
4.b. 環境パラメタ―の相関コブの巾データを「濃い空間」と「希薄空間」に分けた。論文 I ではコブの巾 γ が環境と相関係数 0.72 で強い相関のあることが分かった。 「濃い空間」ではコブの巾が広くなる傾向がある。 線形成分勾配と反り返り強度 図7には c2 = 線形成分勾配と c4 = 反り返り強度 が E(B-V)/r に対してどう変化するかを示した。白丸=濃い空間、反黒丸= トラペジウム、Herschell 36、黒丸=「希薄空間」である。図7(上)は 二つの環境グループが明白に分かれていることを示す。「濃い空間」グループの 勾配のばらつきは大きいが、c2 < 0.5 は全て「濃い空間」グループ である。「希薄空間」グループは比較的大きな勾配に集まっている。 図7(下)は反り返り強度が環境の区分にあまりよく従わないことを 示す。ただ、「濃い空間」の c4 は少し大きいようだ。 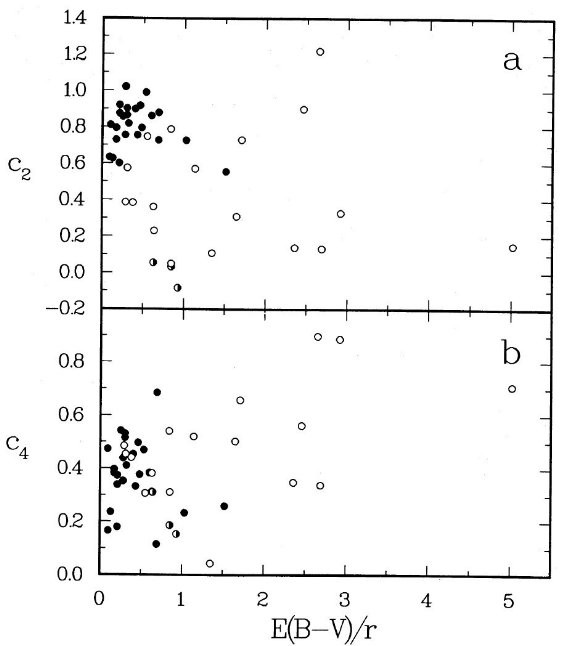 図7.(上):c4 - γ 相関。c4 = FUV 反り返り 強度。γ = コブの巾。白丸=濃い空間、反黒丸= トラペジウム、Herschell 36、黒丸=「希薄空間」 (下):c3 - γ 相関。c3 = コブ強度。 |
|
c1 と c2 の相関の意味 c1 と c2 の相関に対しては二つの解釈が可能である。 (1).一種類のダストが変性して FUV 勾配が変化していく。Seab,Shull 1983 はショックによりシリケイトダストの紫外勾配が変化する説を唱えている。 (2).二つまたはそれ以上の数のダスト種族が存在し、その混合比により 紫外勾配が変化する。その内の一つは FUV でグレイな減光を示し、トラペジウム や HD 147889 はその効果を受けており、別のダスト成分は FUV で線形の 減光を示し、HD 204827 や HD 193322 はその効果が強いと考える。 線形成分の分散 線形成分に関しもう一つ注意すべきは、「希薄空間」では線形成分の パラメタ―が固まっていることである。おそらく「希薄空間」の物理条件が 一様であることを示唆しているのであろう。 |
コブ コブ成分の問題は、コブ部分のみを数学的に分離して取り出しても、それが 物理的にある種族の粒子の減光全てを表しているのかどうか不明なことである。 ただ、HD 147889 のように強いコブを持つが線形成分の勾配がゼロのような 例がある。また、c1、c2 がコブパラメタ―と全く 相関しないこともあり、コブ粒子はコブ領域外では減光に関与しないか、グレイ である可能性が強い。 反り返り成分 反り返り成分の系統的な振る舞いはこれまであまり注目されて来なかった。 反り返り成分の形が同じという本論文の結果は、サイズなどではなく、ある種の 粒子の明確な物理的性質がこの成分に関与していることを示唆する。 おそらく、2175 A のコブより短波長にあるプラズモンの共鳴吸収のウイング であろう。 |