The PL Relation of Galactic Carbon LPVs


Bergeat, Knapik, Rutily
1998 AA 332, L53 - L56



　アブストラクト　

　ヒッパルコス観測のある炭素過多長周期変光星 115 個の (MK, log P) 関係を示す。これを大マゼラン雲の炭素星と較べた所、両者は非常に にており、３本の線が分離した。サンプル１＝ Feast et al. (1989) の関係に近い長周期変光星の系列。サンプル２＝短周期で光度超過の変光星。 サンプル３＝幾つかの光度不足の変光星。用いたデータは Knapik et al 1997 による Lutz-Kelker 効果フリーな期待値を用いた。 　絶対等級の非ガウシアン分布に起因する残りのバイアスは avoid された： 第４章では 72 個のサンプル１に非パラメトリック法を用いて PL 関係を調べ た。結果は
　　MK = -3.99 log P + 2.07
勾配は Reid et al 1995 の値と一致する。この式から得た LMC 距離指数は μ = 18.50 ±0.17 である。サンプル１には等級の上限が 存在する。それは銀河系で -4.85, LMC で -4.72 である。メタル量効果の 補正は加えていない。

　１．イントロダクション　

　これまで　

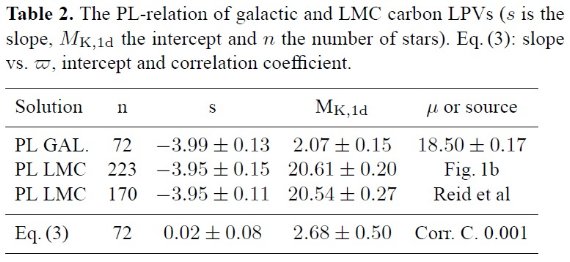
　LMC ミラの PL 関係 は Glass, Lloyd Evans (1981) により発見され、Feast 1984, Feast et al. (1989) で細かく解析された。その関係は ±0.15 mag の巾に収まる。 図１（下）には LMC の観測結果を示す。Groenewegen, Whitelocl 1996 は炭素 過多ミラに対する修正版を出した。彼らのゼロ点は銀河系連星マンバー UV Aur に頼っている。 van Leeuwen et al. (1997) は 16 個のヒッパルコスミラを用いた。サンプル中には炭素星 R Lep が含ま れている。彼らは LMC 距離指数として 18.54 を得た。

　我々のやったこと　

　ヒッパルコスは 115 個の炭素星を観測した。我々はその内、周期が既知の 72 個を用いて PLR を求めた。サンプル１＝ LMC PLR 付近に固まっている星。 破線＝その上限線。サンプル２＝ PLR 上方に集まる短周期星。 Wood, Sebo (1996) は サンプル１を基本振動星、サンプル２を第１倍音振動星と考えた。 Knapik et al 1997 は LPR 下方、暗いサンプル３の真の視差、観測視差 でなく、をバイアスフリーの値として求めた。マルムキストバイアス は、明るい視差 0.6 mas 以上の星では無視できる。

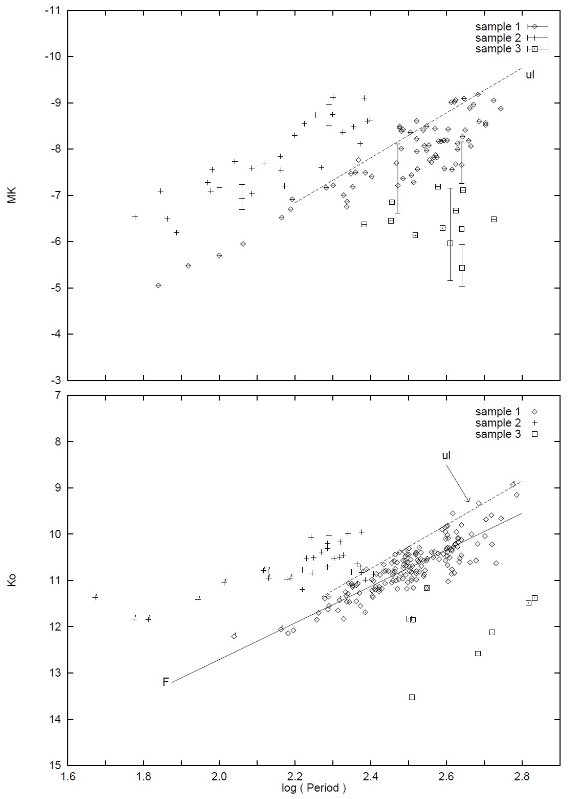
図１．(MK, log P) 図。上：銀河系。下：LMC. 実線＝Feast et al 1989 の PL 関係。破線＝サンプル１の上限線。 　



　２．絶対等級　

　使用した 115 星のデータは表１に示すが、これは CDS から取ってこられる。 入力事項は、スティーフェンソンカタログ番号、周期、MK、 第４章で決める y 値、真の視差評価値 ω(mas)、観測視差との差 Δ ω である。 　

　３．MK - log P 関係　

　３．１．３つのサンプル　

　データ　

　ミラと SR の周期は GCVS とヒッパルコスカタログから採った。表１の ．MK と log P の関係を図１(a) に示す。図１(b) には LMC 炭素 過多星について同様の図を示した。両者の間には強い類似性がある。参照のため 通常の MK - log P 関係も示した。

　LMC サンプル　

　大部分の LMC 炭素星は PLR の周りに集まり、サンプル１を形成する。この 帯は log P > 2.4 では上限が付いている。また、log P < 2.4 ではサ ンプル２のため上方に広がる。PLR の下にはいくつかのサンプル３星が固まっ ている。

　銀河系サンプル　

　LMC と同じ３つのサンプルが銀河系でも見られる。ただし、その数比　 (72, 31, 12) は LMC での (190, 32, 11) とは異なる。銀河系サンプルの 視差のエラー、分類の不確かさ、などの影響は大きいだろう。その結果 全体的にはサンプル１から 2, 3 への流出効果はあるであろう。注意したいの は、2.4 < log P の炭素星ミラ 19 個の内サンプル２は一つもないことで ある。一般に炭素星ミラの振幅は酸素過多星ミラよりも小さい。振幅と周期は 相関するので、長周期変光炭素星がミラに分類されるためには長い周期が必要 になる。 		　振動モード　

　 Wood, Sebo (1996) は LMC のサンプル２は倍音振動星で、他の星は倍音振動と考えた。 van Leeuwen et al. (1997) は恒星半径対周期図に基づいて、７個のミラ型星の振動モードを決めた。 仮にその M-型ミラのモデル半径・周期関係が炭素星にも適用可能とすると、 Dyck, van Bell, Benson (1996) がセミレギュラー、イレギュラー炭素星の干渉計による視直径と仮定した L = 104 Lo から決めた炭素星半径 400 Ro から、 サンプル２の星は倍音振動していると推測される。
(400 Ro は セミレギュラー炭素星半径 を 104 Lo の仮定で決めたもので、ここに引用するのが適当かどうか 疑問)


　３．２．暗いサンプル３　

　暗さの確かさ　

　周期光度図上で 12/115 星は暗い右下部を占める。ただし、周期と絶対等級 の不定性を考慮する必要がある。さらに、 Knapik et al 1997 の真の視差の 期待値というのは統計的な意味でのみ正しいことも考えなければいけない。 不定性にも拘わらず、 C 2064 = RU Pup がサンプル１の３等下にあることは この星がサンプル１より明らかに暗いことを示す。ミラでは、 C 2165 = T Lyn が標準エラーの２倍離れて暗い。

　種族差　

　サンプル間に明らかな種族差を示す速度の違いは認められなかった。また、 スペクトル型やカラーにも大きな差はなかった。

　４．PLR と LMC 距離指数　

　サンプル１の勾配とゼロ点　

　サンプル１の周期光度関係の勾配とゼロ点を求めたい。注意すべきことは、 視差のガウシャンエラーが、距離や絶対等級に非ガウシャンエラーとして 伝播していくことである。こてを避けるため、フィットの式は、

　　　y = f(x) = exp(ax+b)　　　　　　（１）

の形とする。ここに、 x = log P, y = ω 100.2 Ko, a = 0.2 ln(10)× s, b = 0.2 ln(10) [MK,1d + 10]. ω ＝真の視差の推定値、は表１から。 MK,1d ＝周期１日の星が持つ であろう絶対等級。s = PLR の勾配。（１）式への非線形フィット から a, b を決め、ｓを求める。

　MW と LMC の PLR 比較　

　図１（ｂ）には３．１節の炭素星へのフィットと、Reid et al 1995 による O-, C-LPV に対する PLR の結果と示すが、両者の勾配はほぼ同じである。 従って、両者の差を LMC の距離指数として採用することを薦める。その値は 18.50±0.17 である。Feast et al 1996 が様々な系からの証拠を基に 結論したようにここでもメタル量補正は行わない。

表２．銀河系と LMC の炭素星 PLR. n = 星数。 s = 勾配。MK,1d = 切片。Eq(3) は相関。

　５．結論　

　炭素星長周期変光星 115 個の真の視差に対する推定値を求めた。19/115 個 はミラ型星である。変光星は３つの集団に分かれる。
　サンプル３中、最も暗い星は TP-AGB 星進化モデルに厳しい制限を提示する。それらは初期質量 1 - 3 Mo であったが、激しい質量放出の結果 M ≤ 0.8 Mo になった残存星かも知れない。 		　PLR の勾配は銀河系と大マゼラン雲とでは同じであった。二つの PLR を同一 として導いた距離指数 18.50±0.17 は van Leeuwen et al. (1997) が、酸素過多ミラから出した 18.54±0.18、 Feast, Catchpole 1997 が セファイドから導いた 18.7±0.1 と近い。