First Results from HIPPARCOS Trigonometrical Parallaxes of Mira-Type Variables

　アブストラクト　

　１．イントロダクションと観測　

サンプル星　 　ミラ PLR のゼロ点を定めるために用いた１６個のミラを表１に載せた。 内 10 個は普通の M-型ミラ、１個 = χ Cyg は S-型ミラ、２個＝ R Hya, R Aql は周期がゆっくり減少している M-型ミラでヘリウムフラッシュ中では ないかと想像されている。残り３個のうち、１個 R Cen は酸素過多だが深い 極小と浅い極小を交互に繰り返す。 R Aqr は酸素過多ミラでシンビオティック 系に属する。最後の R Lep は炭素過多ミラである。それらの幾つかは視直径 も測られている。 　ＪＨＫＬ測光　 　サンプル星は全て SAAO 0.75 m を使い、 SAAO 測光系等級が求められた。 表１には赤化補正した等級が載せてある。表には最高と最低の平均を取った。 減光は Feast, Whitelock, Carter (1990) の手法で決めた。そこでは、 　　E(B-V) = 0.032(cosec|b|-1)[1-exp(-10rsin|b|)] ただし、M-巨星とSR の Mv = -0.5 仮定して r 決定、が用いられている。

表１．１６個のミラ

　２．ミラ型星の実半径　

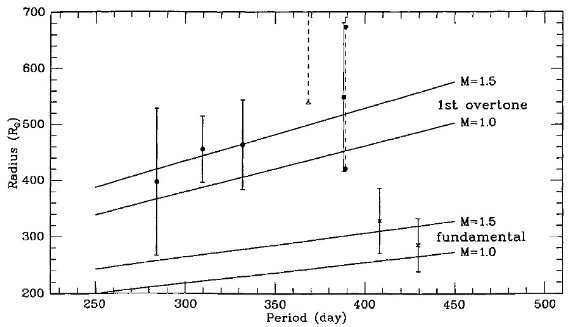
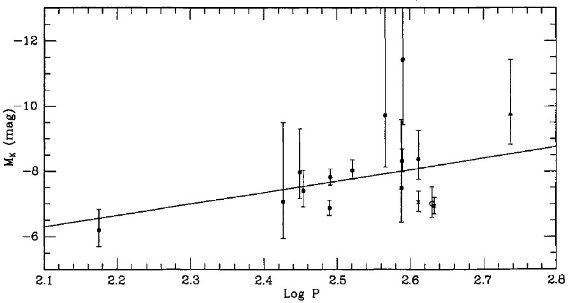
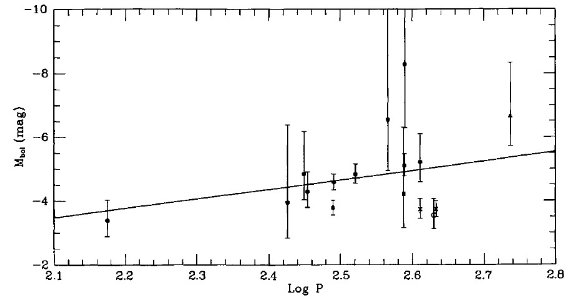
図１＝周期・半径関係　 　Haniff et al 1995 はサンプル星中の８個の視直径を決めた。表１に載せて ある。視直径とヒッパルコス視差とから導いた実半径を表２に載せた。 図１にはこれ等の星の周期・半径関係を示す。運動学 Feast 1963 や他の証拠 Feast, Whitelock 1987 はミラ型星が低質量星であることを示唆している。 　基本振動と第１倍音　 　図１には質量 1.0, 1.5 Mo 星の基本振動と第１倍音の半径も示す。 基本振動は Wood 1990 から採った。 　　　log P = 1.949 log R - 0.9 log M - 2.07 第１倍音は Q = 0.04 とした標準式、Fox, Wood 1982 と似た、 　　　log P = 1.5 log R - 0.5 log M + log Q を用いた。 　ミラの振動モード　 　視角観測と PLR から導いた距離を使った実半径はミラが第１倍音で揺れている Feast (1996) ことを強く支持する。しかし、ミラ輝線から示唆される衝撃波は基本振動モデル でのみ再現される。Ya'ari, Tuchman 1996 は上の式で仮定されるような単純な モデルでは不十分であると主張した。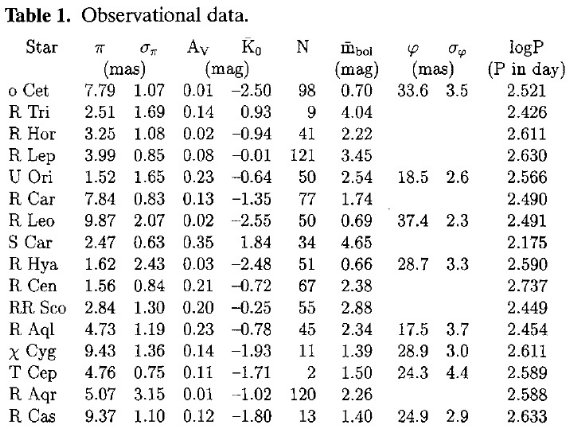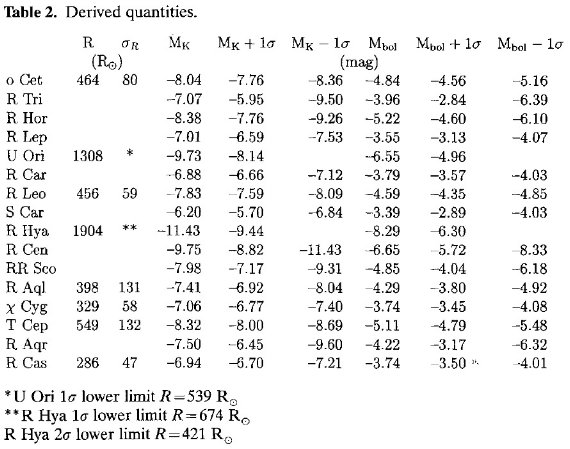 表２．観測から導いた量

グループ分け　 　図１を見ると、ミラは３つのグループに分かれる。P > 400 d の ミラ χ Cyg と R Cas は基本振動ラインの上にある。一方、 R Aql, R Leo, ο Cet, T Cep は第１倍音域にある。U Ori と R Hya の半径は非常に 大きいが、どうじに不定性も大きい。したがって、それらが第１倍音ライン に乗る可能性も否定できない。 　基本モードの確実性　 　視角の決定にはミラの大気モデルが必要で、表２では第１振動の "E" モデル の値を採用した。従って、基本振動ではないかと疑われる χ Cyg 329 Ro, R Cas 286 Ro が適当かどうか怪しい。もし基本振動の "D" モデルを採用すると、 χ Cyg 374 Ro, R Cas 328 Ro となり、基本振動ラインとの一致は少し悪く なる。しかしその差は小さい。その上、"D" モデルは "E" モデルよりかなり熱 くなる。 χ と R Cas が同じ周期の他のミラ型星に較べ熱いという証拠は ない。したがって、"D" モデルが適切かどうか不明である。我々の結論は、 ヒッパルコス視差に基づくと、この二つの星は図１の他の星と異なるモード ＝基本振動で振動しているということである。 　ミラは倍音！　 　以上の結果から、 P < 400d のミラの大部分は倍音振動しているが、 幾つかは基本振動を行っている。星が基本モードと倍音モード領域に 落ちることはかなり簡単なモデルで脈動の記述が出来ることを示唆している。 ただし、するとミラの輝線が生じるメカニズムは不明になる。 図１．ミラの周期・半径関係。黒丸＝ R Aql, R Leo, ο Cet, T Cep. バツ＝ χ Cyg, R Cas. 三角＝ U Ori の 1σ 下限。アステリスク＝ R Hya の 1σ, 2σ 下限。

　３．ミラの周期・光度関係　

図２．MK - log P 関係。実線＝ LMC PLR を DM=18.50 で変換したもの。 黒丸＝通常のM-ミラ。白丸＝炭素ミラ R Lep. 黒四角＝シンビオティックミラ R Aqr. 黒三角＝二重周期ミラ R Cen. バツ＝基本振動星 χ Cyg, R Cas. 　ゼロ点　 　Wood 1990 は理論的根拠から銀河系ミラの Mbol は LMC ミラより 0.4 mag 暗いとした。多くの研究でこの補正が使用された。しかし、 Feast (1996) はこの結論は最終的ではないと指摘した。また、Whitelock et al 1994 は銀河系 と LMC で PLR のゼロ点は殆ど変らないことを見出した。さらに Wood 1995 は SMC と LMC の間でゼロ点が同じことを見出した。 　サンプル　　 　図２，３にあるように、 χ Cyg, R Cas は振動モードが違う。また、 R Aqr, R Cen, R Lep は特殊である。そこで、残りの正常な酸素過多ミラ型星 11 個を PLR 決定に用いた。しかし、サンプル数の不足から勾配まで決める に至らず、 Feast et al 1989 の LMC ミラに対する PLR の傾きを固定して 使う。 　フィット式　 　　　MK = -3.47 log P + β1 　　　Mbol = -3.00 log P + β2 サンプル点の重みの付け方でフィットしたゼロ点が変わる。それらを表３に まとめた。

図３．Mbol - log P 関係。実線＝ LMC PLR を DM=18.50 で変換したもの。 表３．ミラ PLR のゼロ点と結果としての LMC 距離指数。 　LMC 距離　 　表３の解３をとると、LMC の距離指数は 18.57 となる。この値はセファイド から導かれた 18.57 に近い。この事実はメタル量効果がないという仮説を 強く支持するものである。もう一つ注意すべきは Mbol から 決めた距離指数は MK から決めた距離指数より 0.1 mag 小さい。 同様の効果は SGP で Whitelock et al 1994, Sgr I で Glass et al 1995 が 見出している。これは同じ周期に対するカラーの差が原因らしく、一種の メタル効果と言える。

　４．基本振動星と他の星