|
新しい星間ダストモデルを示す。モデルは FUV から NIR までの減光と拡散
赤外放射を同時にフィットする。以前のモデルと異なる点は元素組成の拘束を
満たすことである。減光フィット問題は典型的な "ill-posed" 逆変換問題で、
粒径分布が未知なので正規化法で解いた。ダストモデルは以下の成分から成る： （１）ＰＡＨ （２）シリケイト （３）非晶質炭素 （４）複合組成＝シリケイト＋非揮発性有機物＋水氷＋穴 各成分の光学的性質を光学定数を用いて計算した。特別な場合として Li, Draine (2001) を再現した。 しかし、彼らのモデルではダスト内に含まれる Si, Mg, Fe の量がそれぞれ 50 ppm (100 万水素原子当たりの原子数)必要で、宇宙存在比 Si = 34, Mg = 35, Fe = 28 ppm を越えてしまう。 |
この論文の主な結論は観測される減光、拡散赤外放射、宇宙組成を同時に満
たす星間ダストモデルが一意には決まらないということである。これらの制限
に適合するいくつかの種類のダストモデルを見つけた。第１種は Li-Draine
モデルと同じ構成で、PAH, グラファイト、シリケイトから成るが彼らのモデル
とはサイズ分布が異なる。その結果、元素量制限をクリアできた。第２種はそ
れに複合粒子を加えたものである。他の種類のモデルでは、グラファイトの代
わりに非晶質炭素を使用したり、PAH 以外では炭素を全く含まなかったりする。 全てのモデルは、太陽、F-, G-型星元素組成の制限に抵触しないが、B-型星 に関しては困難である。炭素なしモデルのみが B-型星からの制限をクリアする。 他の観測的制限、例えば星間偏光、X-線散乱などからモデル間の優劣を決定でき る可能性がある。 |
|
MRN モデル Mathis, Rumpl, Nordsieck 1977 の MRN モデルは最近まで最も一般的に使用 されてきた。そのサイズ分布は a = [5, 250] nm 区間で a-3.5 で ある。それに必要な元素量は C = 370, Mg = 34, Si = 35, Fe = 28 ppm で あり、太陽組成では炭素の殆どを消費する。 MRN モデルの欠陥 IRAS の希薄星間光の観測結果を熱平衡にあるダストからの放射と較べると、 12, 25 μm に超過があることがわかった。 Draine, Anderson 1985 は MRN サイズ分布を半径 5 A まで伸ばすことでこの矛盾を解決しようとした。 新しく導入された VSG = Very Small Grain は温度搖動を示す。 Tielens, Baker 1985, Leger, Puget 1984 は VSG を PAH 分子であるとした。 PAH は 3.3, 6.7, 7.6, 8.6, 11.3 μm 放射の源として想定された 物質である。ただし、 Tokunaga 1997 が述べているように PAH は完全な承認 を得ているわけではない。 Desert, Boulanger, Puget 1990 モデル ダスト成分に PAH を加えたモデル。仮想的な光学定数を使用している。 |
Li, Greenberg 1997 モデル PAH を加え、円筒形シリケイトに不揮発性有機物をコート。減光と偏光を説明し、 組成制限もクリア。拡散赤外放射の説明は行っていない。 2200 A のコブを説明 するのに仮想的な光学定数を導入している。Kim, Martin 1995 も偏光の 説明を試みた。 Dwek et al 1997 Dwek et al 1997 はシリケイト、グラファイト、PAH モデルで星間減光と拡散 赤外放射を説明した。光学定数には シリケイト、グラファイトには Draine, Lee (1984) を、PAH には Desert et al 1990 を使用した。主に UV での PAH の非物理的 な性質が原因で、このモデルは減光曲線の再現に至らなかった。 Draine, Li 2001 と Li, Draine 2001b Draine, Li 2001 と Li, Draine 2001b は PAH の光学定数により現実的な 実験データを採用して、モデルの改良を計った。しかし、彼らのモデルは Mg, si, Fe を太陽組成以上に必要とする。特に鉄は２倍要るのが問題である。 |
|
定義 NH = H のコラム密度 ∫fi(a)da = H １個当たりの i-種粒子の個数。 ρi = i-種物質の質量密度 ∫(4/3)πa3ρifi(a)da = H １個 当たりの i-種粒子の総質量 Qii(λ, a) = i-種半径a 粒子の減光効率 τ(λ) = 光学的深さ I(λ) = 輻射強度 Ei(λ, a) = i-種、半径 a ダストの放射率 希薄星間空間中のダストの性質を探るに当たっては以下の３つの式による制限が 課せられる。 １．平均光学的深さ τ(λ) H 1個コラム密度当たりの光学的深さは
= Σi∫Kτi (λ,a) fi (a)da (1) |
２．輻射強度 I 希薄星間空間からの赤外輻射強度 I は
= Σi∫KIi (λ,a) fi (a)da (2) 放射率は Ei (λ, a) = ∫dU P(a, U) B[λ,T(U,a)] ここに T(U, a) = 内部エネルギー U, 半径 a の温度、 P(a, U) = U の確率分布。 非常に小さなダスト粒子では、温度が確率論的に変動する。 ３．ダストに含まれる元素量
= Σi∫ Kji (a) fi (a) da (6) ここに、 mj = j-元素の原子量、αj, i = i- ダスト中にある j-元素の質量比である。 |
|
スーパーカーネル 整理のため、もう一度書き直すと
これまでに出てきた Kτ, KI, Kj (j = 1, 2, ...,k) を１つのスーパーカーネル K(x, a) にまとめる。 確認しておくが、 i はダスト番号で 1 から n, j は元素番号で 1 から k まで ある。 |
すると、 K(x, a) = [ {Kτ1(λext,a) ,...,Kτn(λext,a)}, {KI1(λem,a) ,...,KIn(a)}, {K11(a)...., K1n(a)},..., {Kk1(a),...,Kkn(a) ] 上にあるように、 x = {λextmin, ..., λextmax, λemmin, ..., λemmax, 1, 2,...,k} を一般化変数と考える。最後の 1 - k はダスト構成元素の列を示す。 D(x) = [τ(λextmin), ..., τ(λextmax)]/NH, [I (λemmin), ..., I (λemmin)]/NH, [N1, ..., Nk] /NH F(a) = [ f1 (a), ..., fn (a) ] として、次の積分方程式に全体をまとめられる。 D(x) = ∫K(x, a) F(a) da (8) |
|
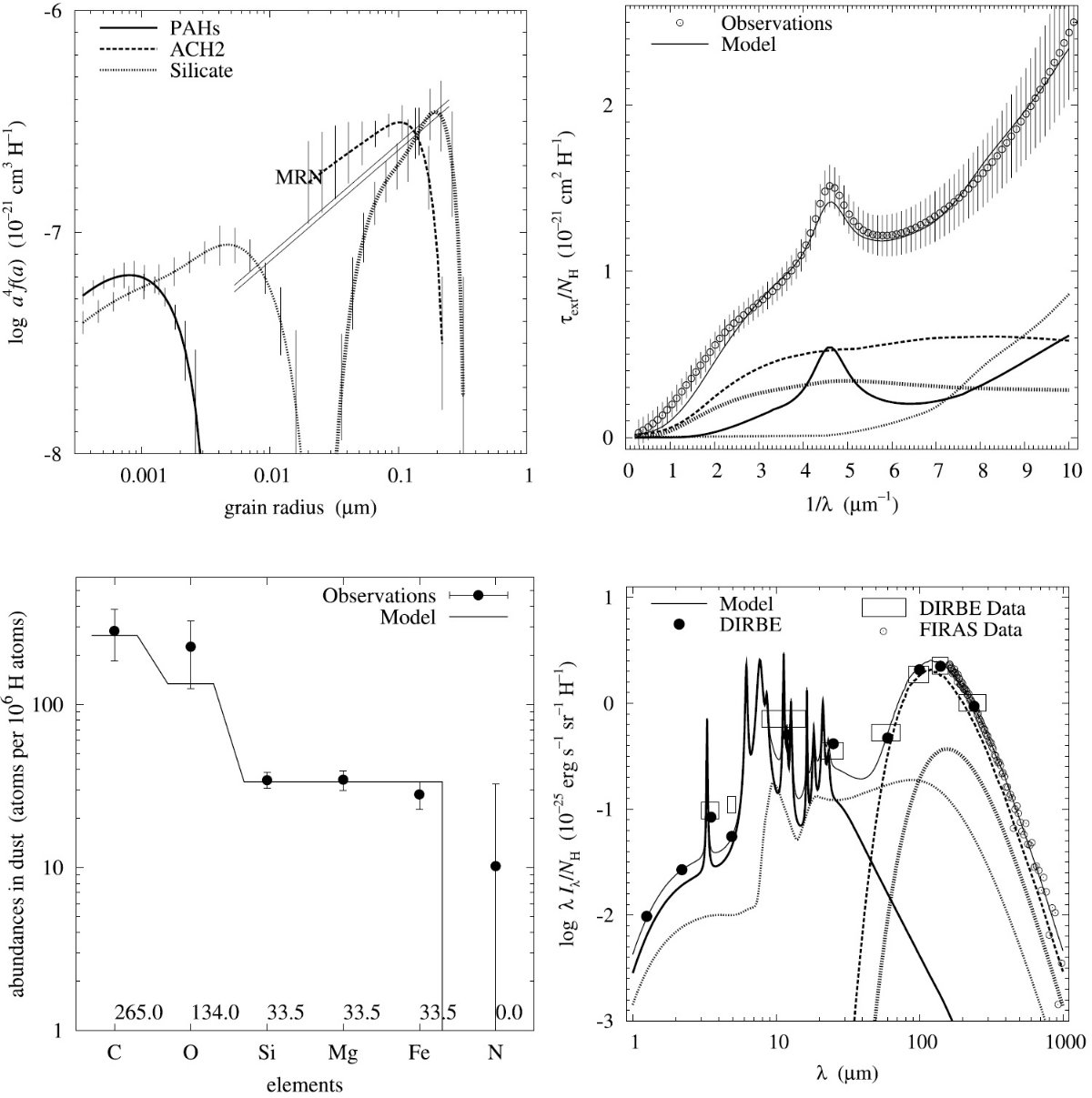
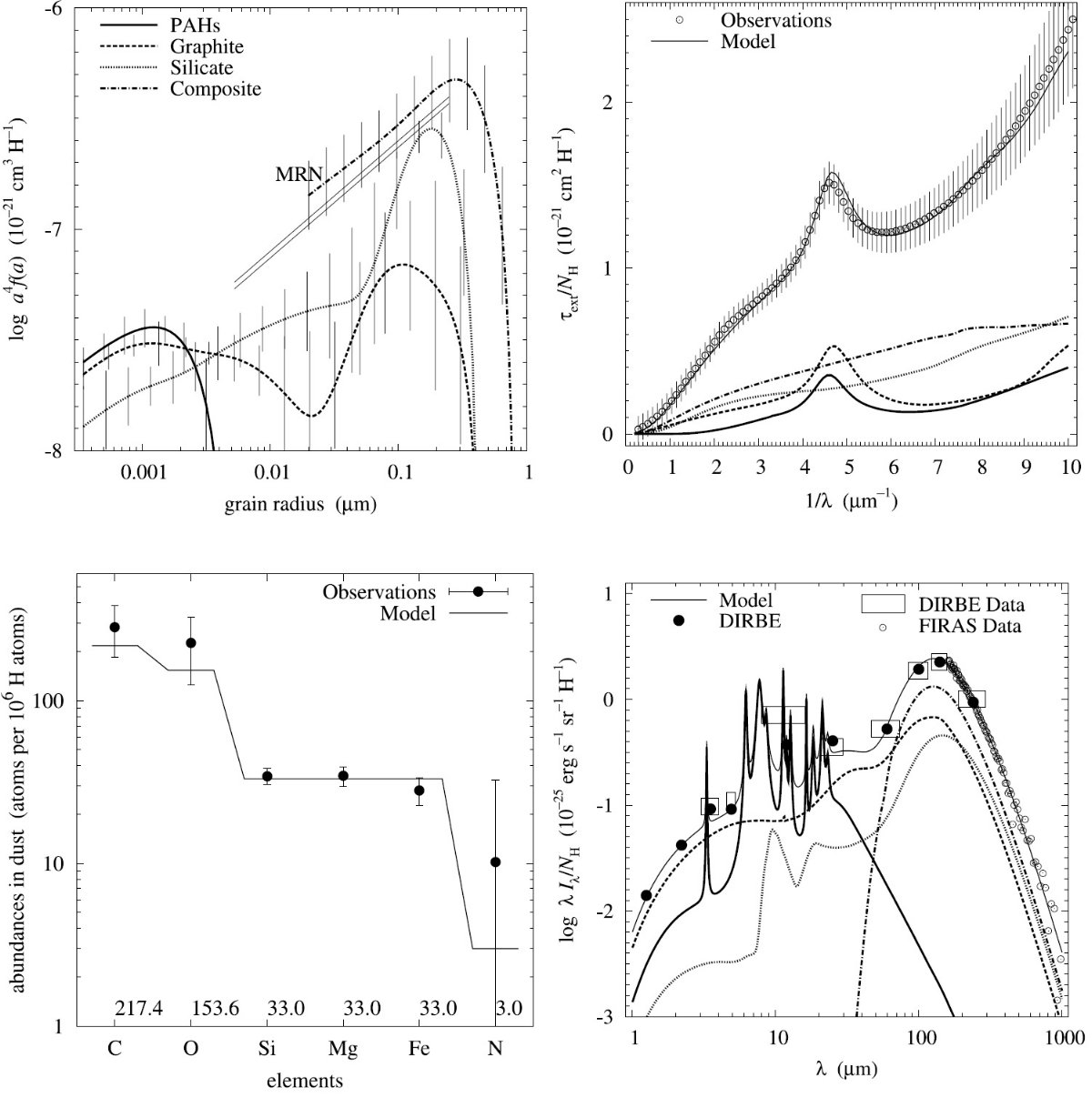
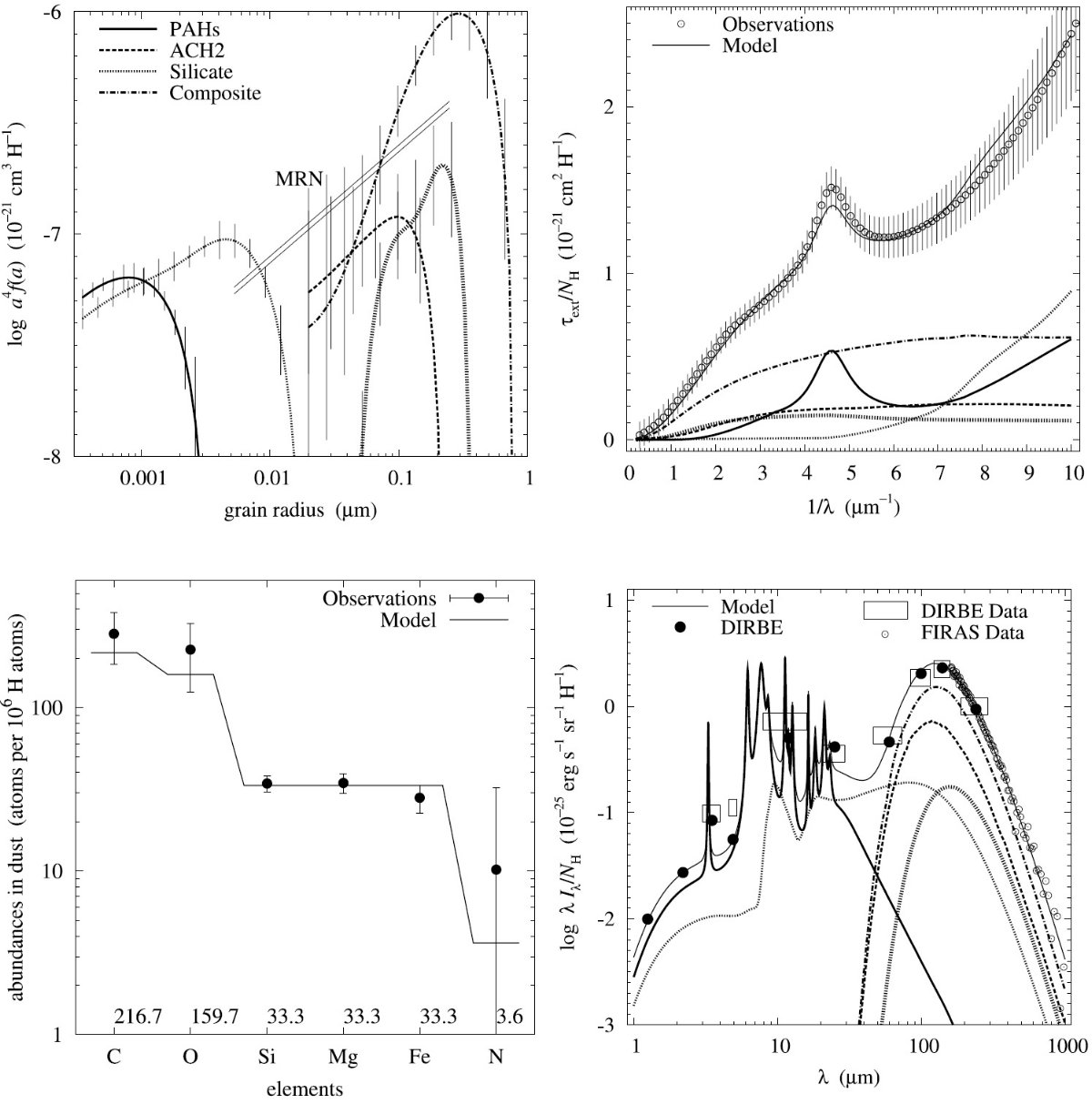
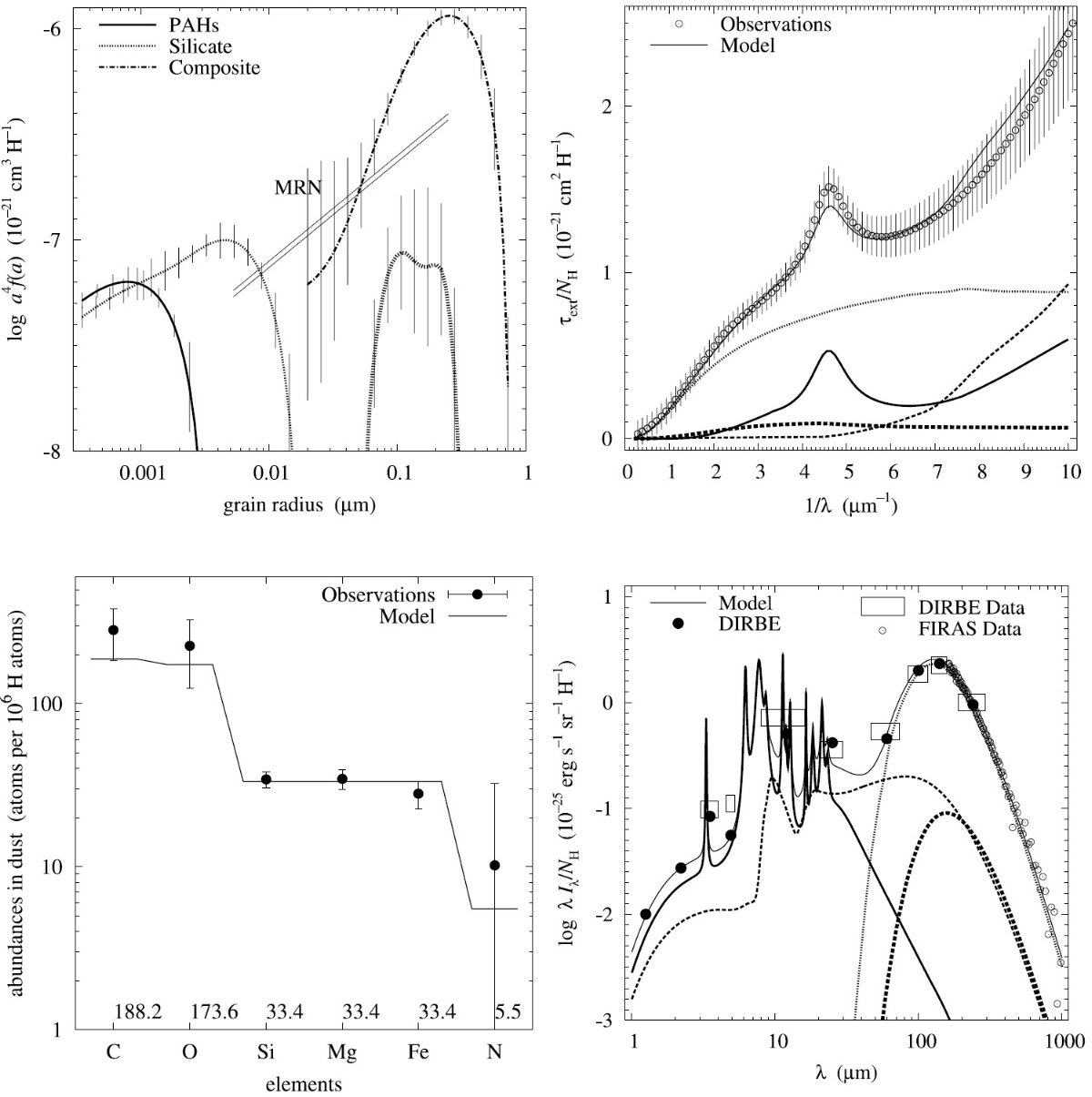
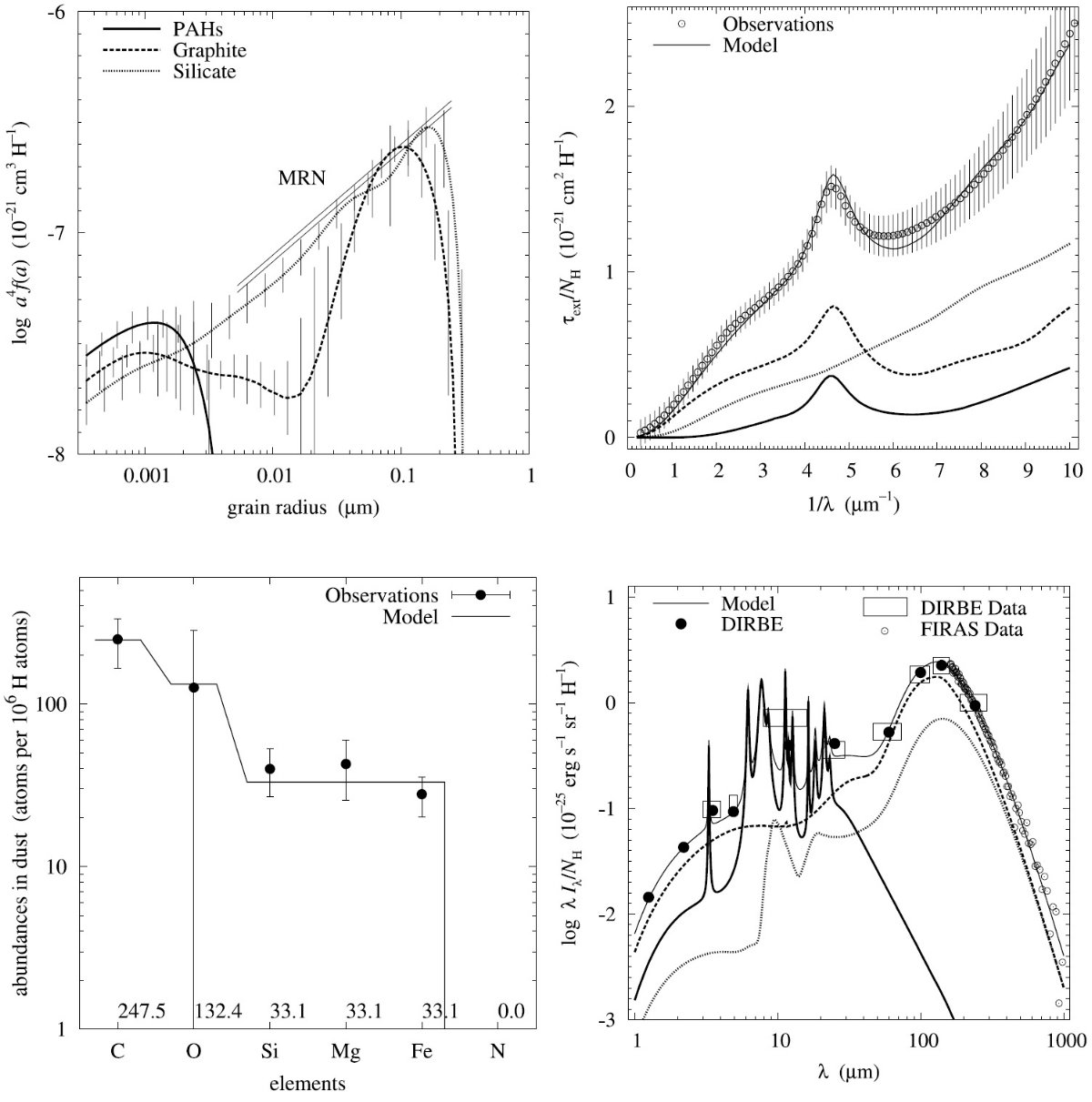
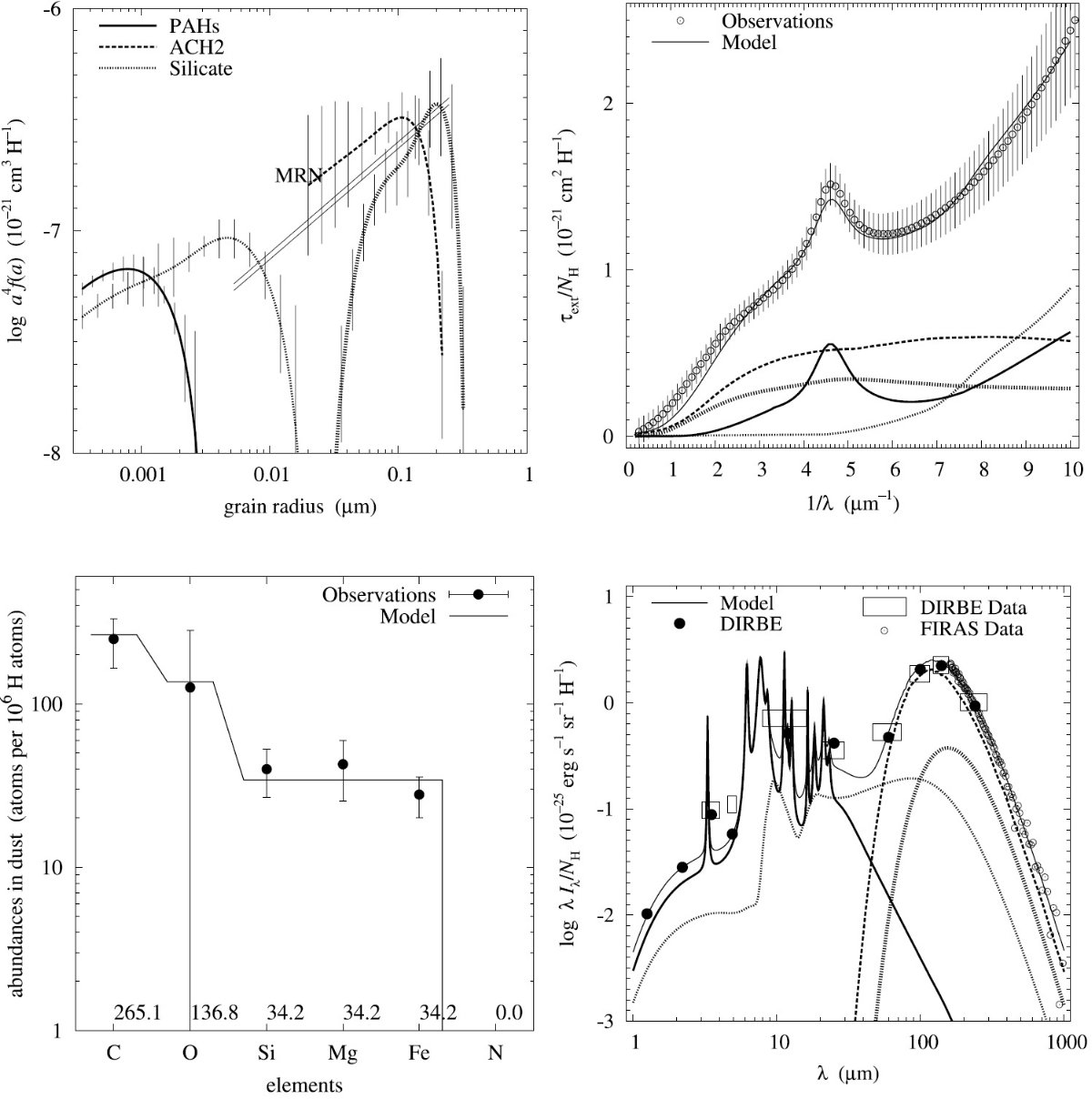
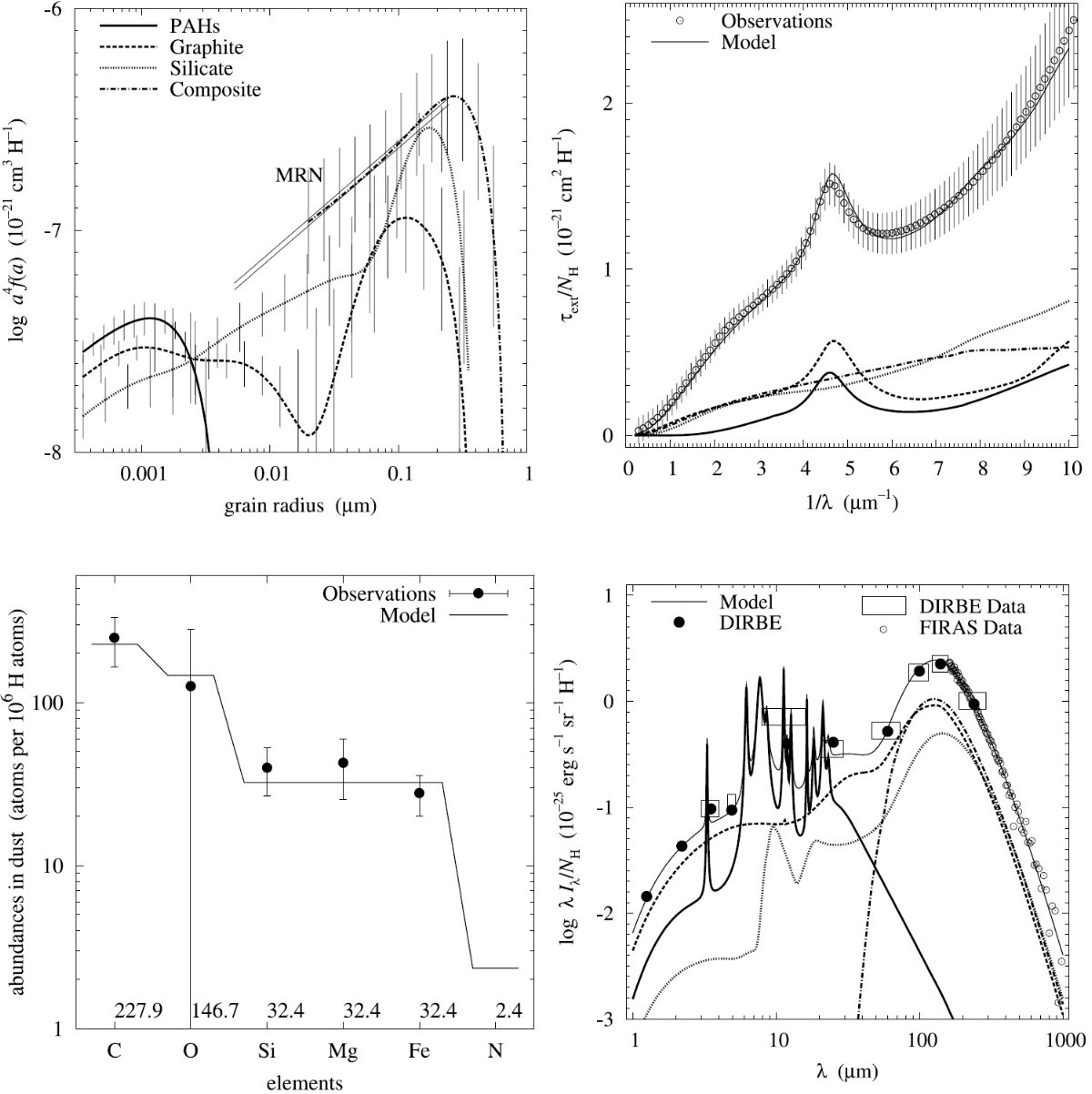
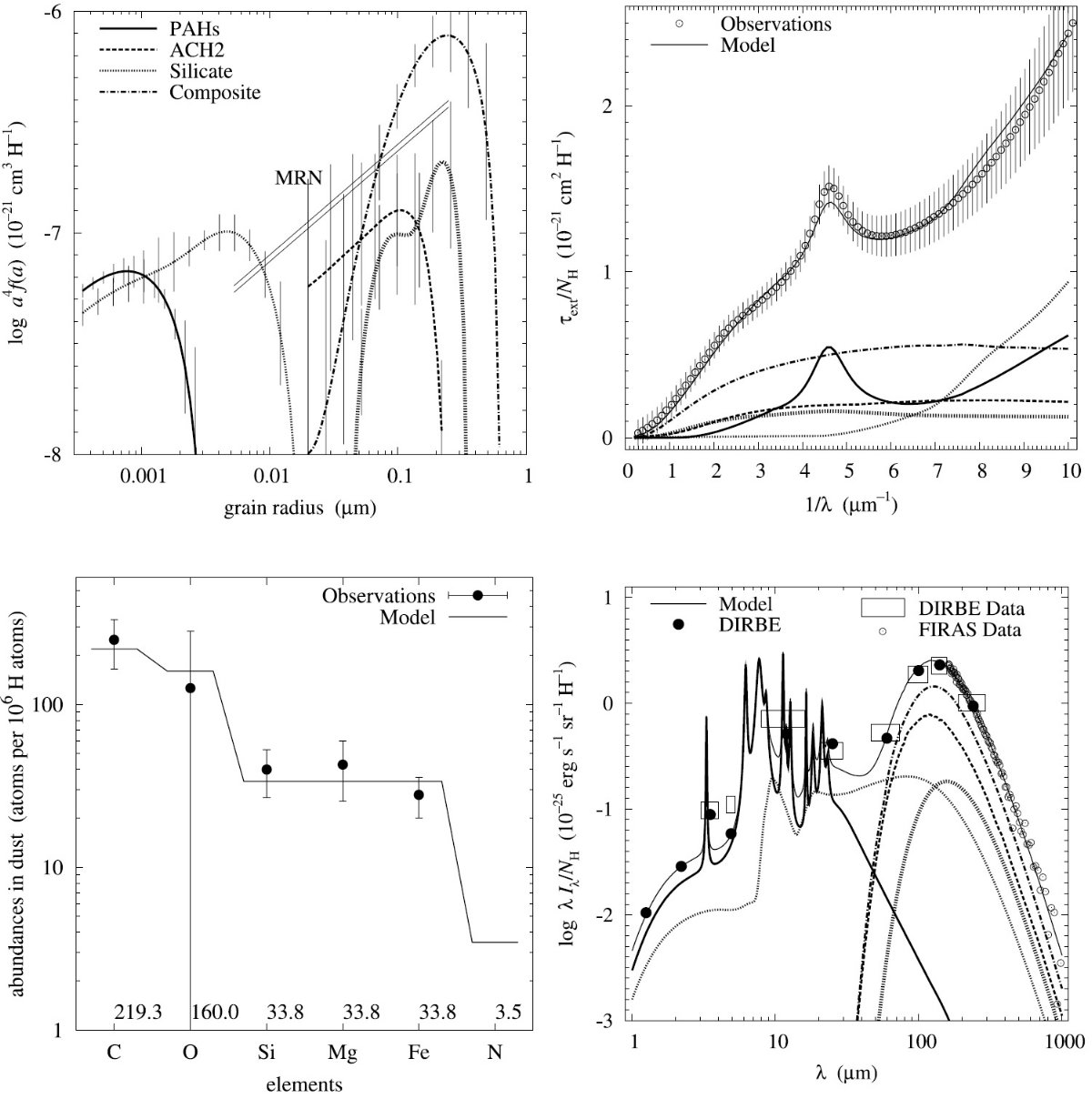
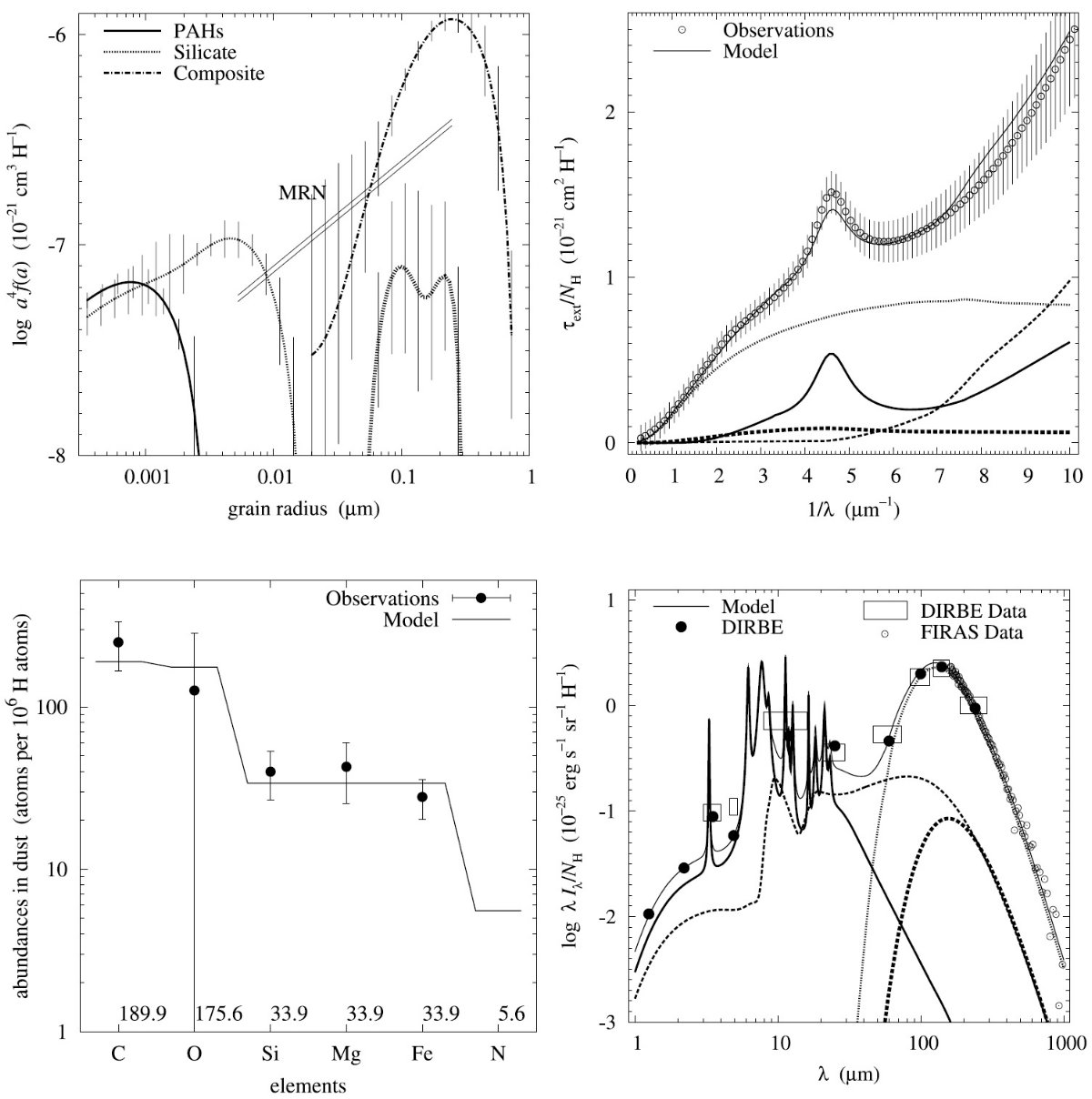
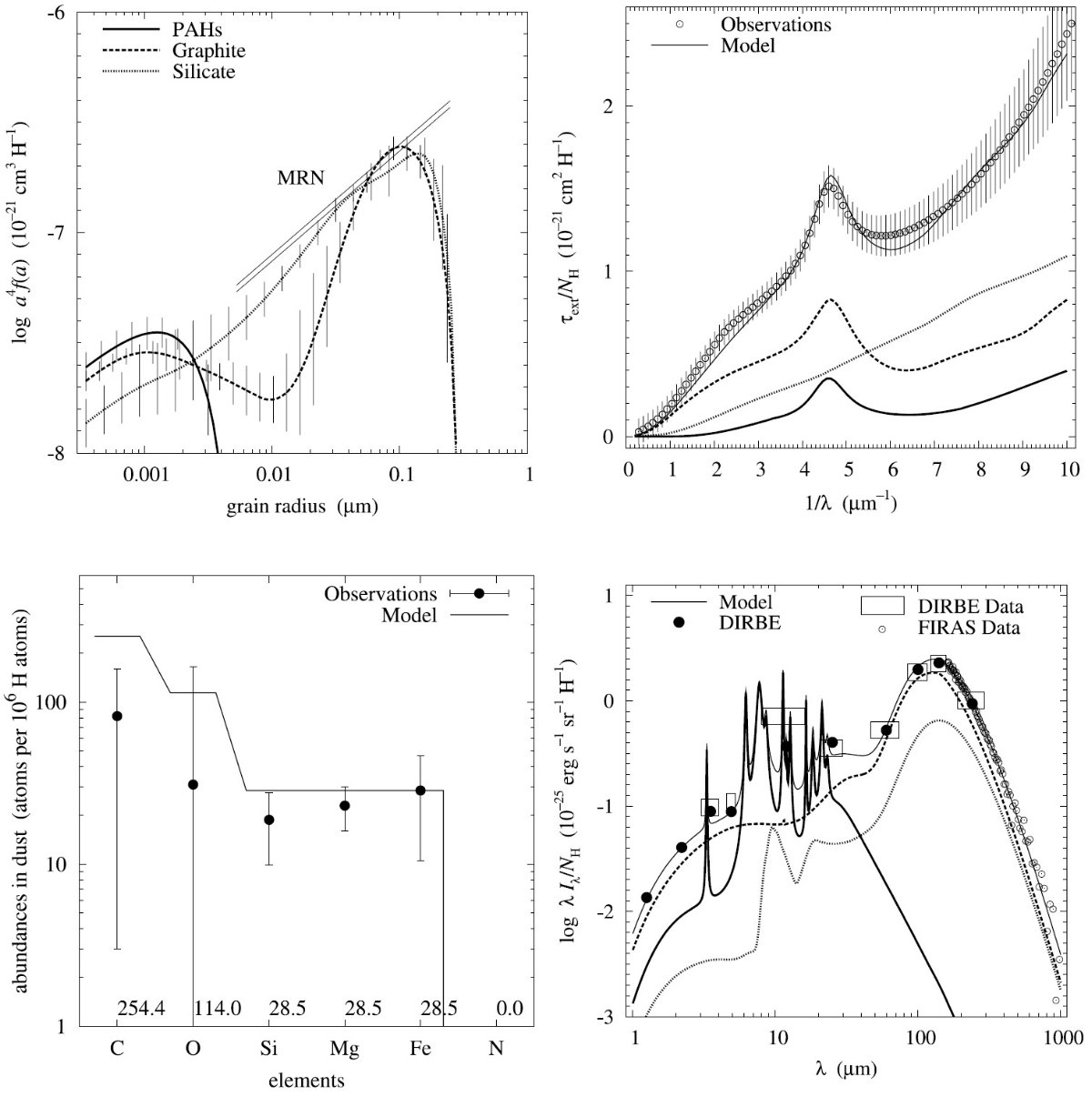
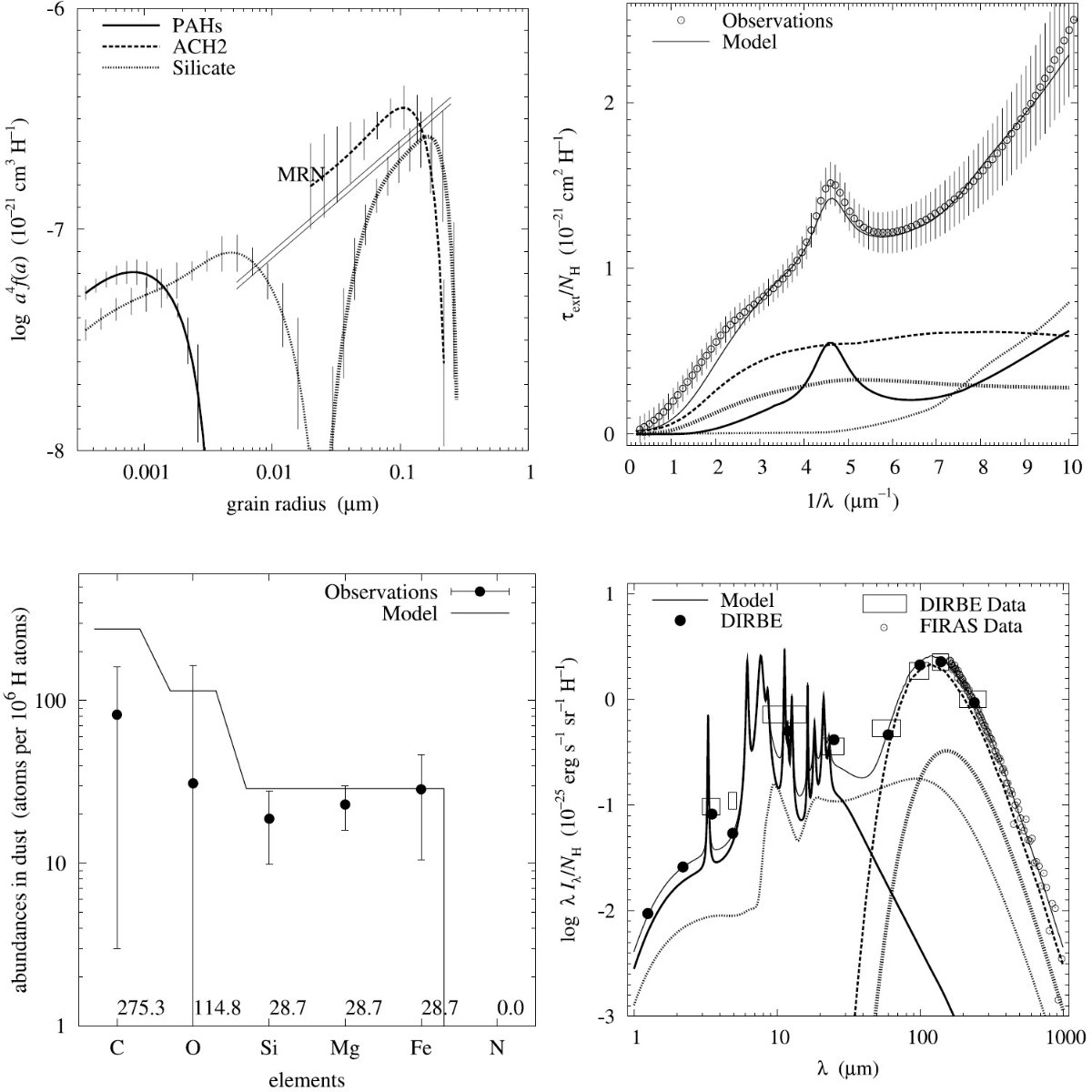
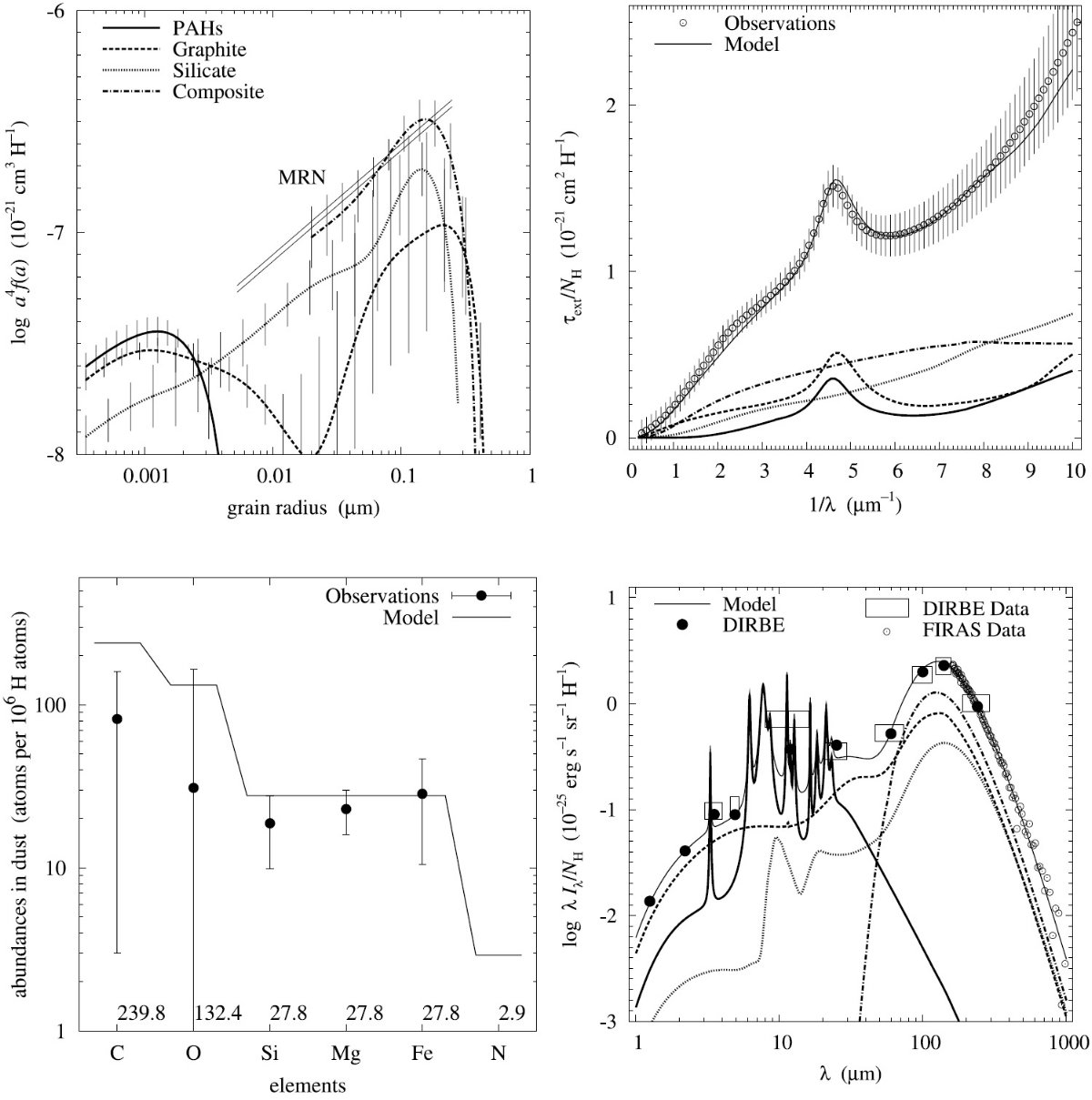
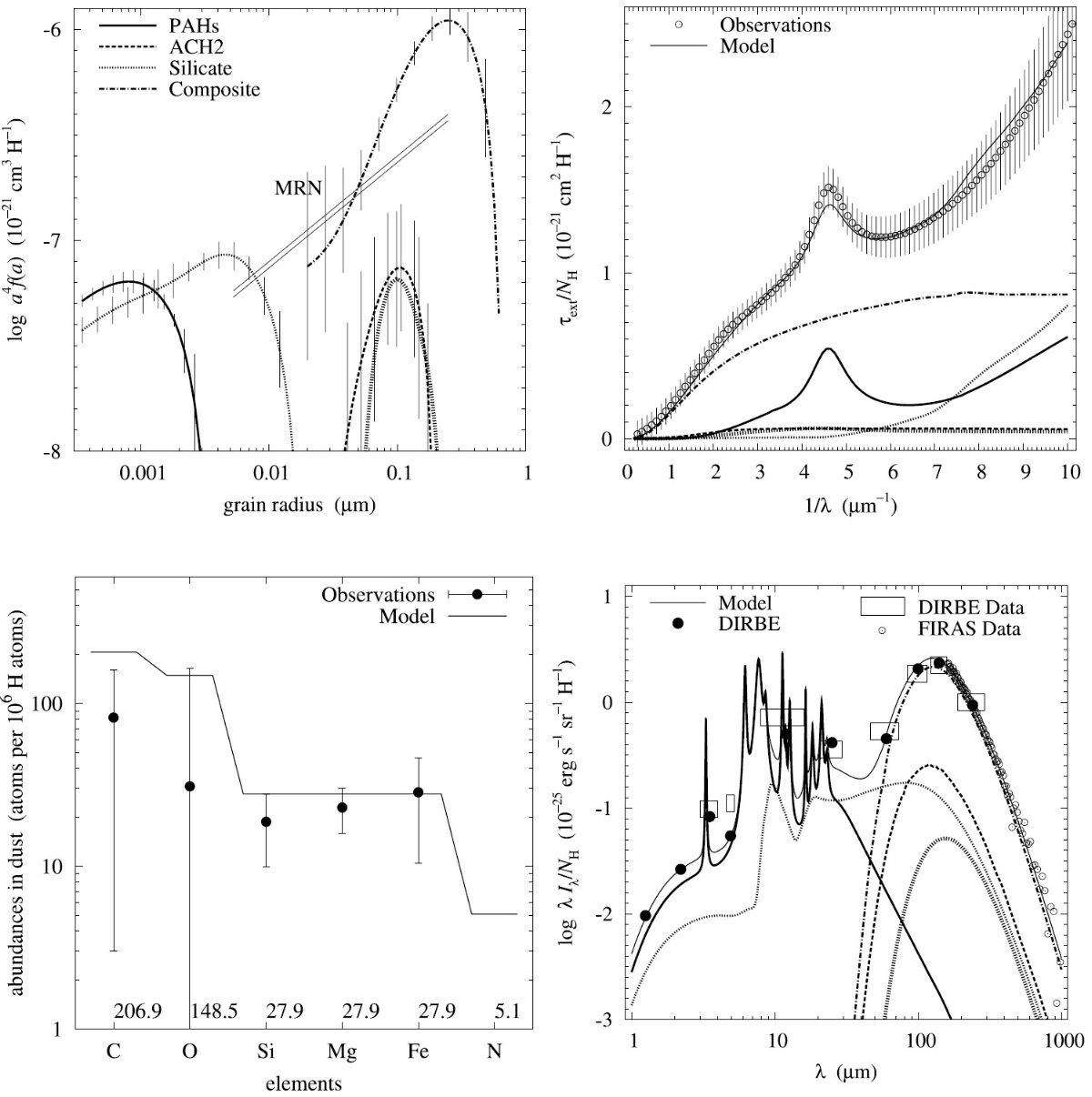
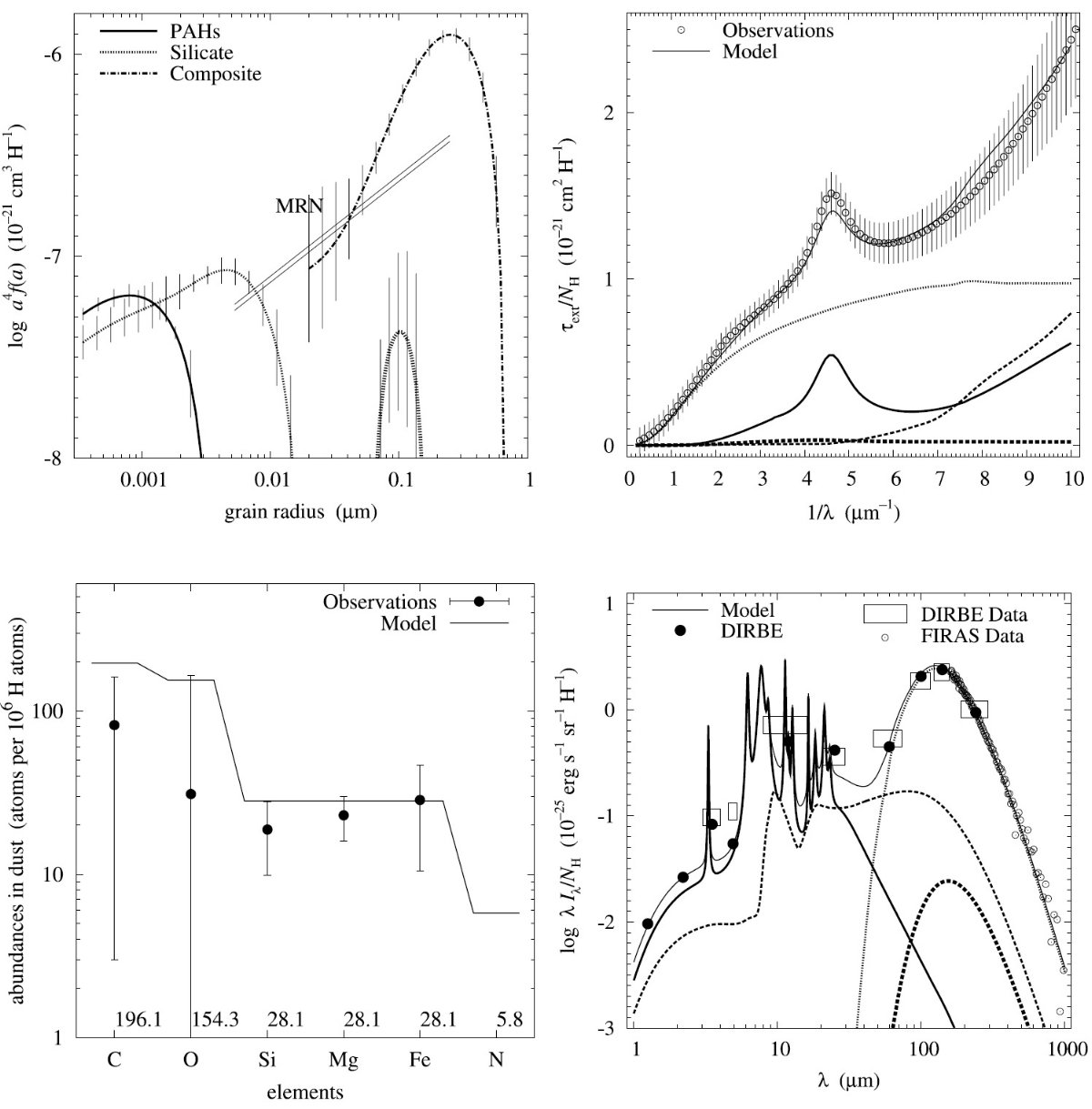
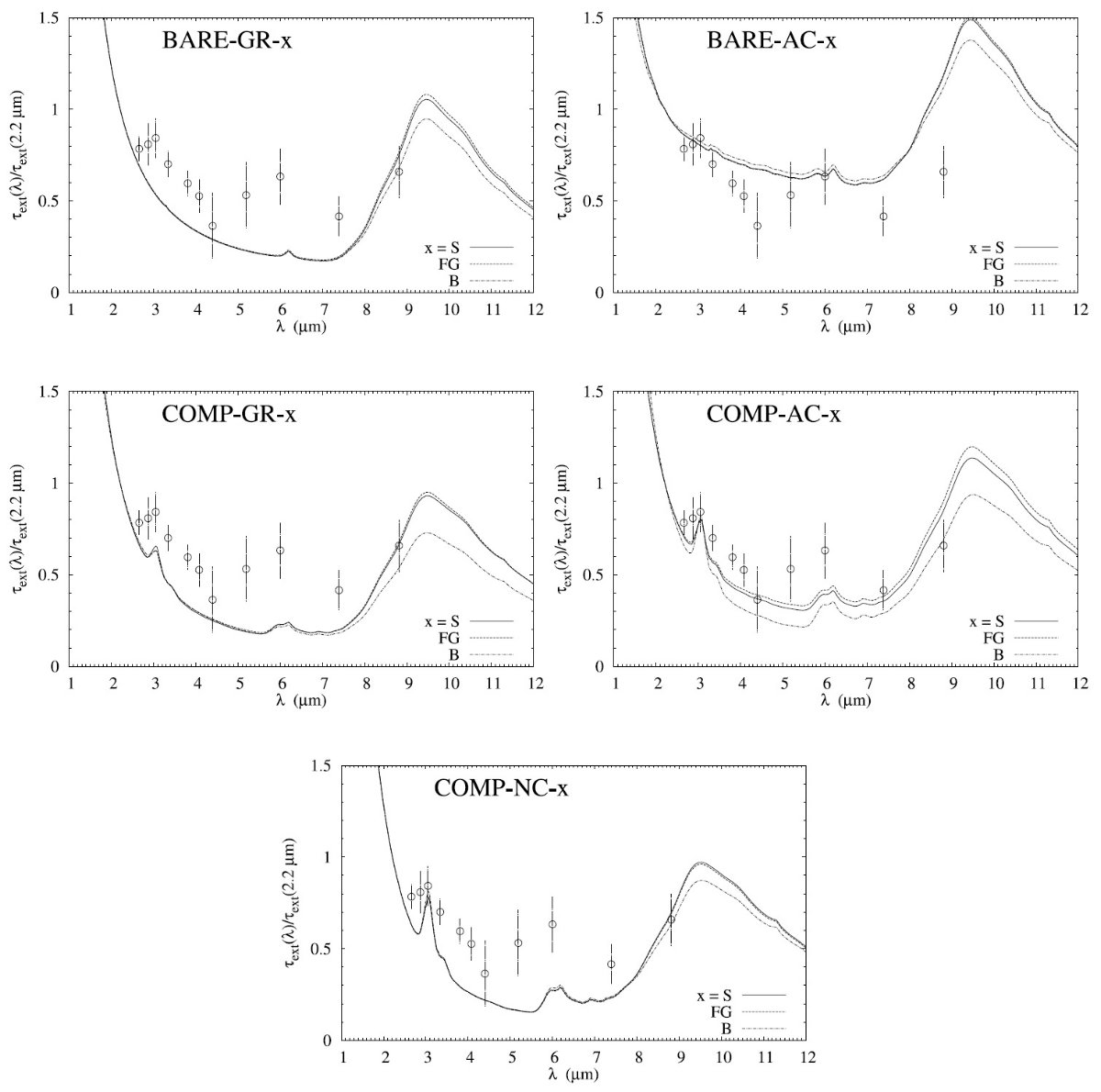
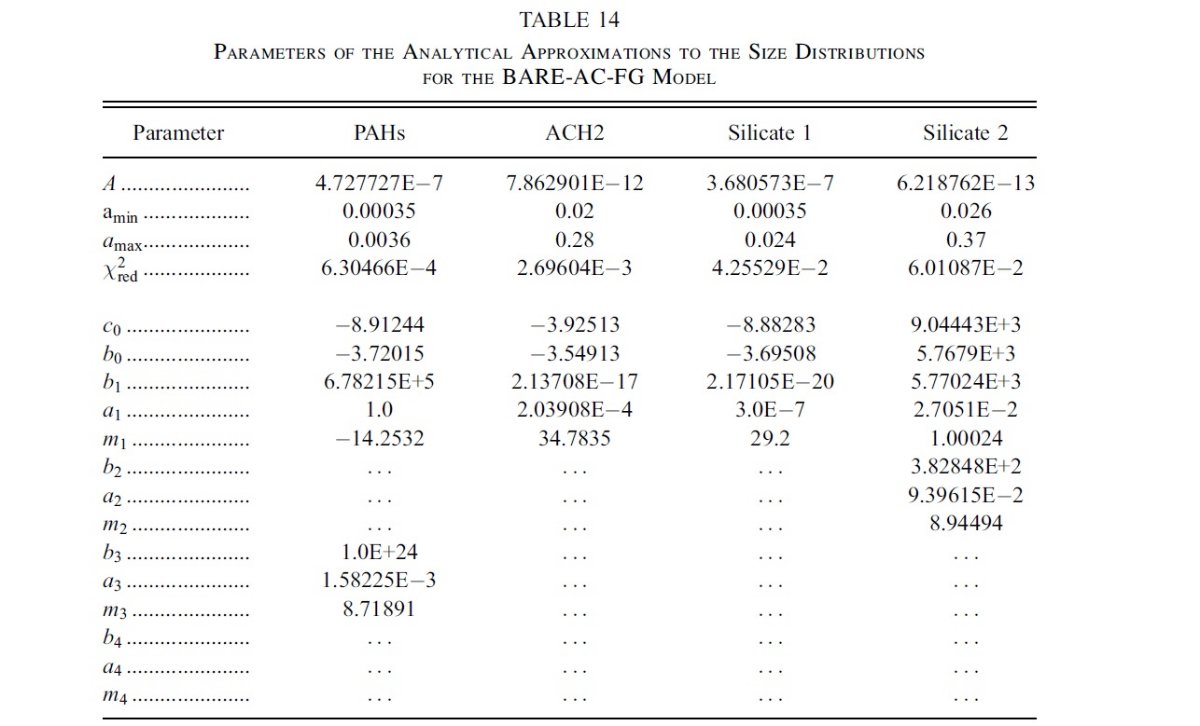
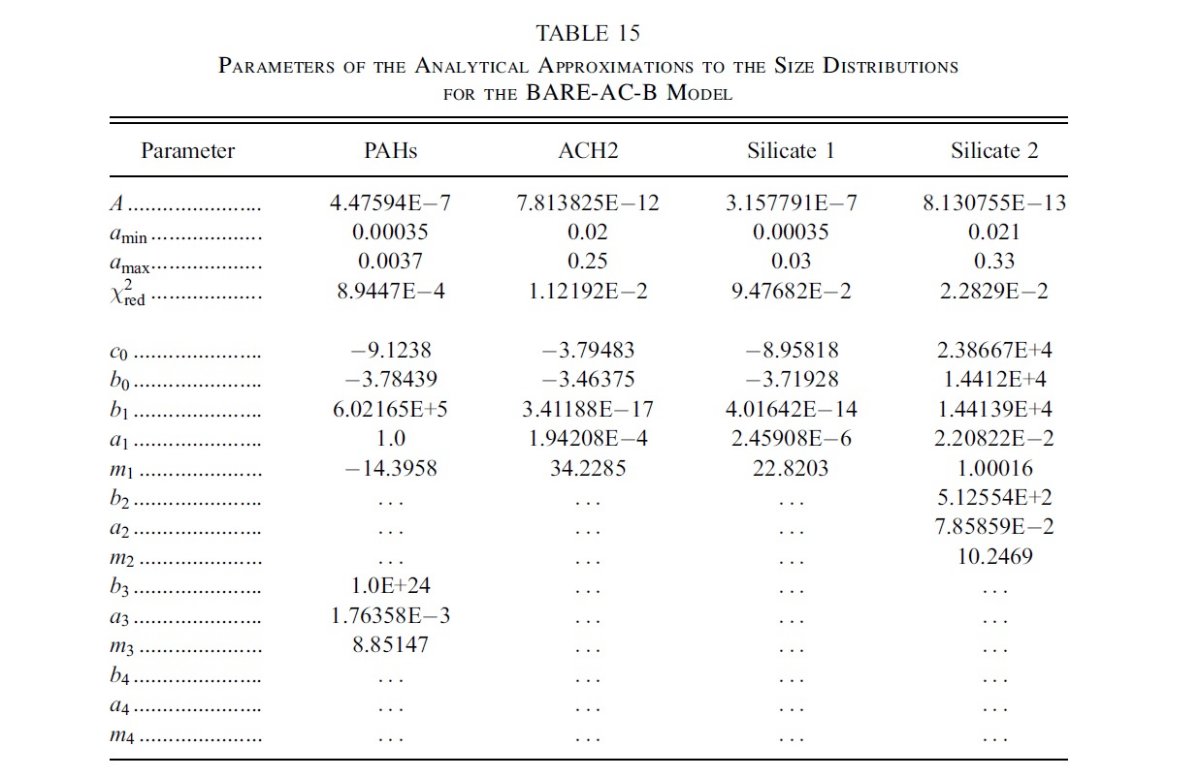
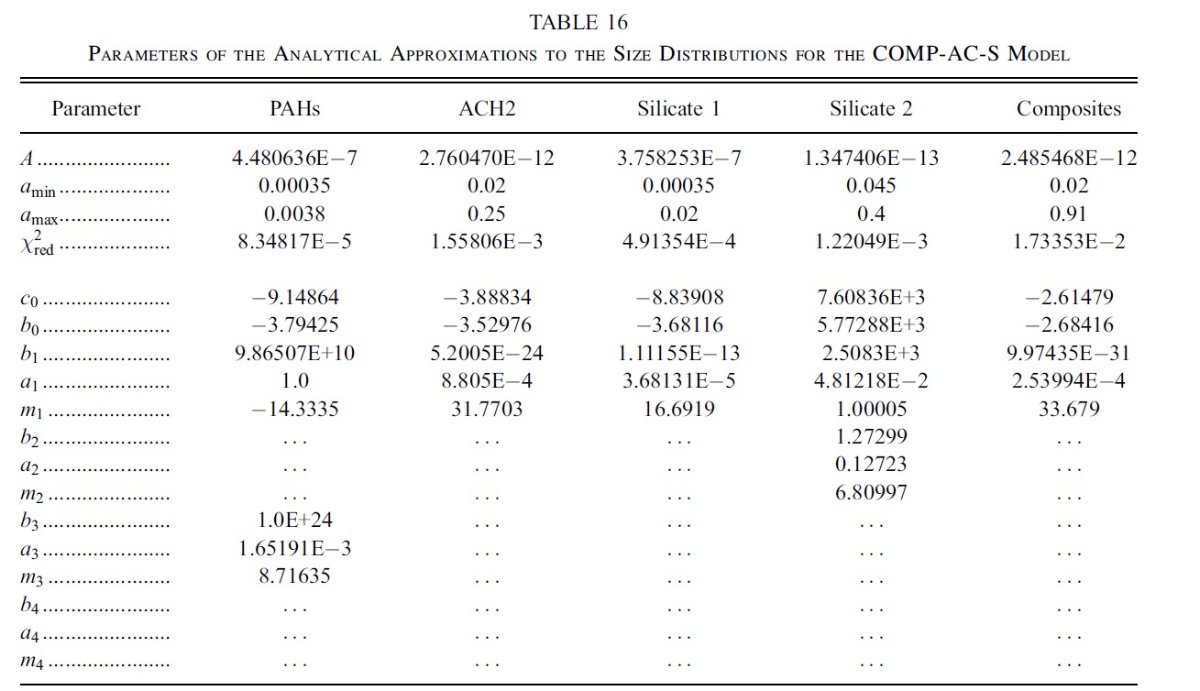
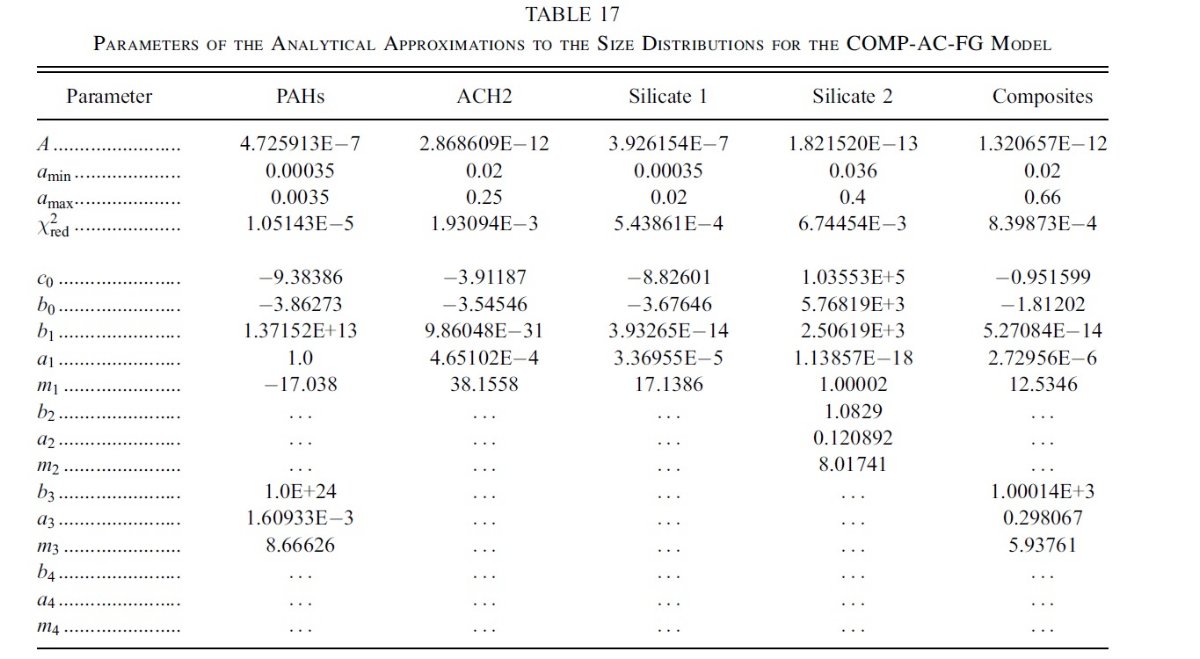
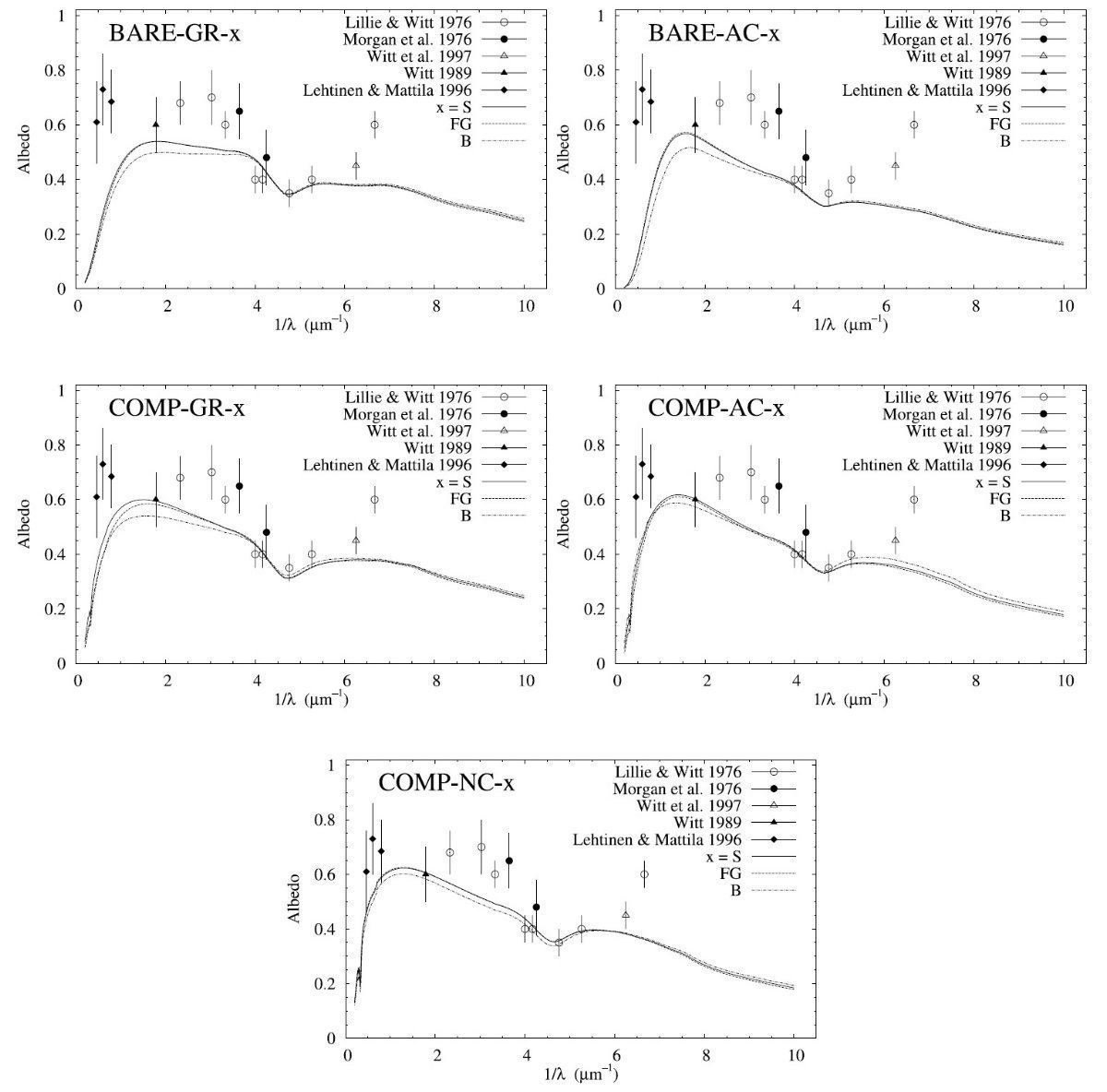
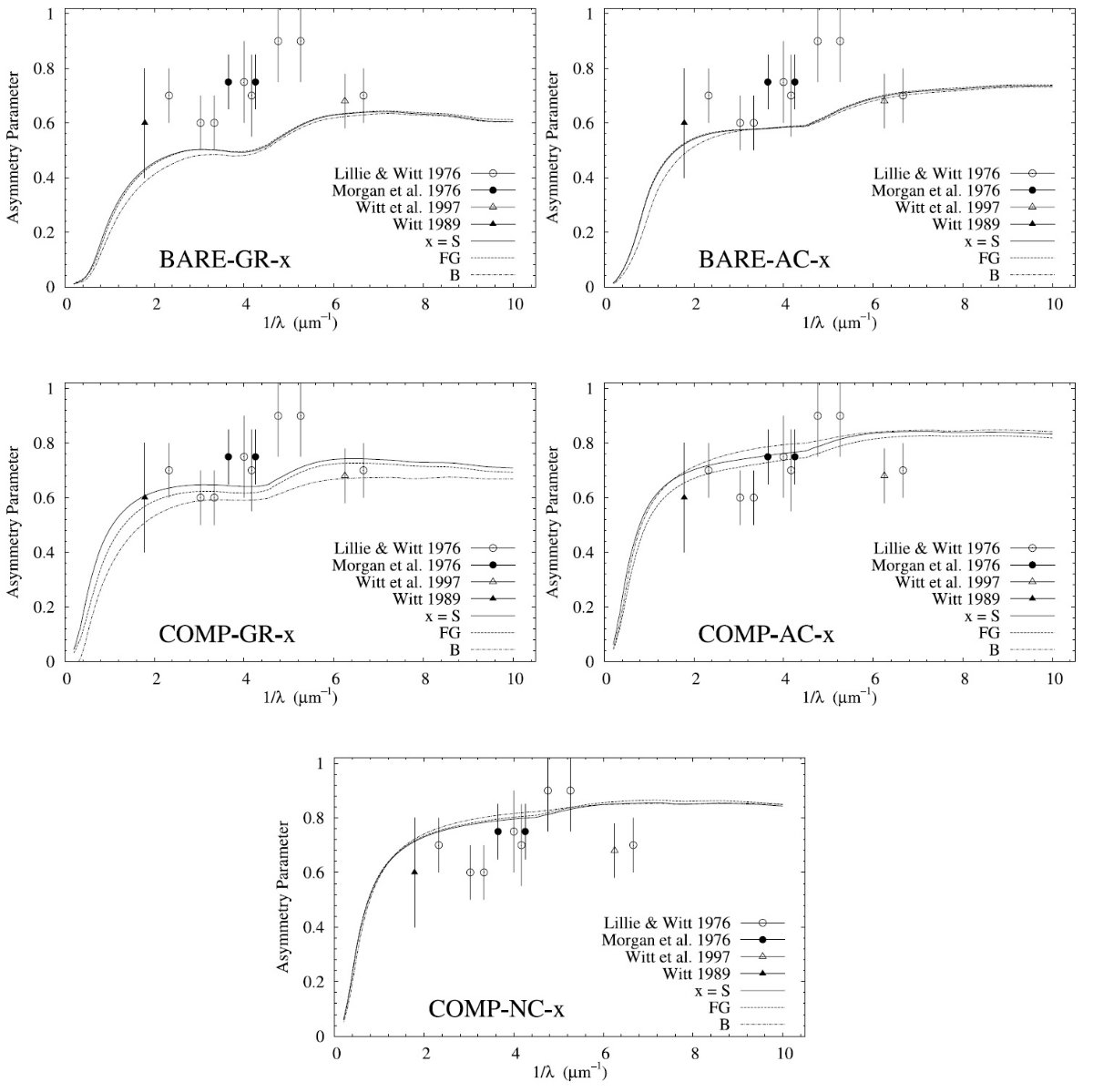
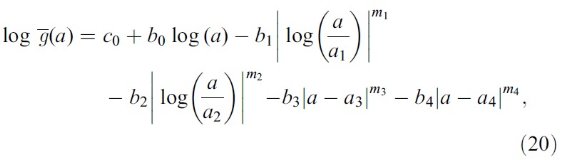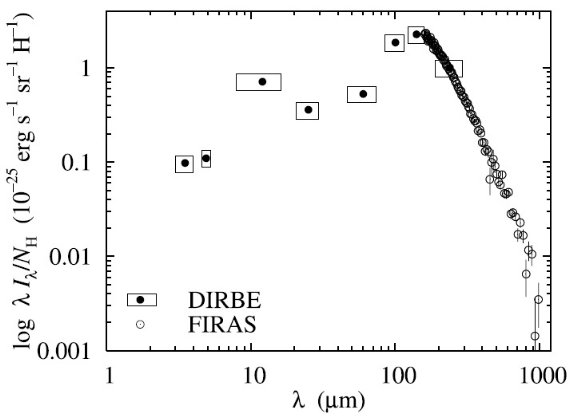
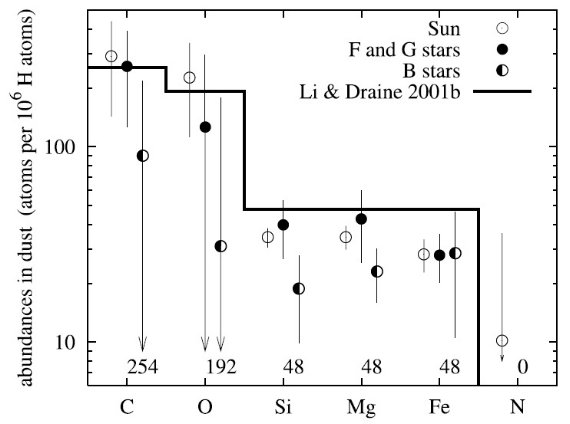
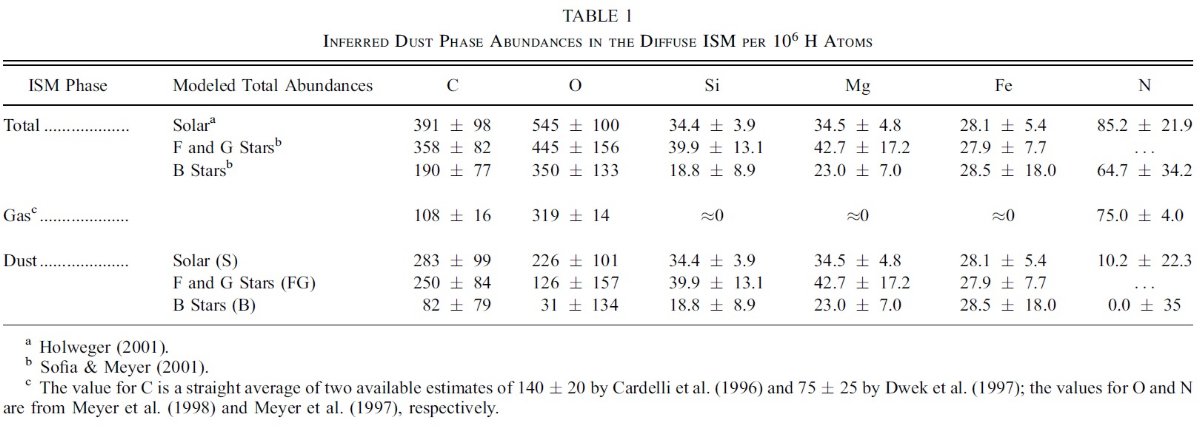
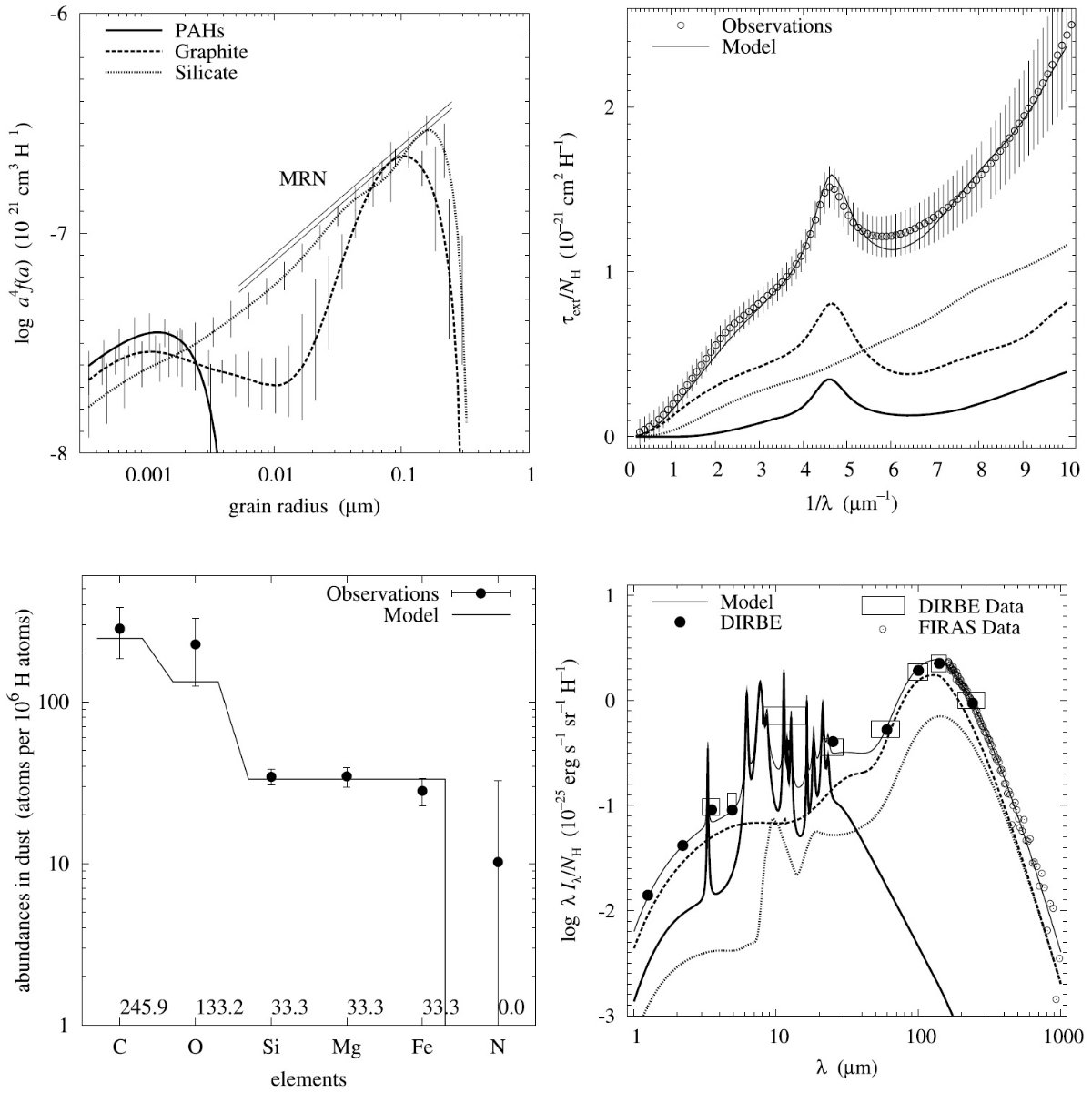
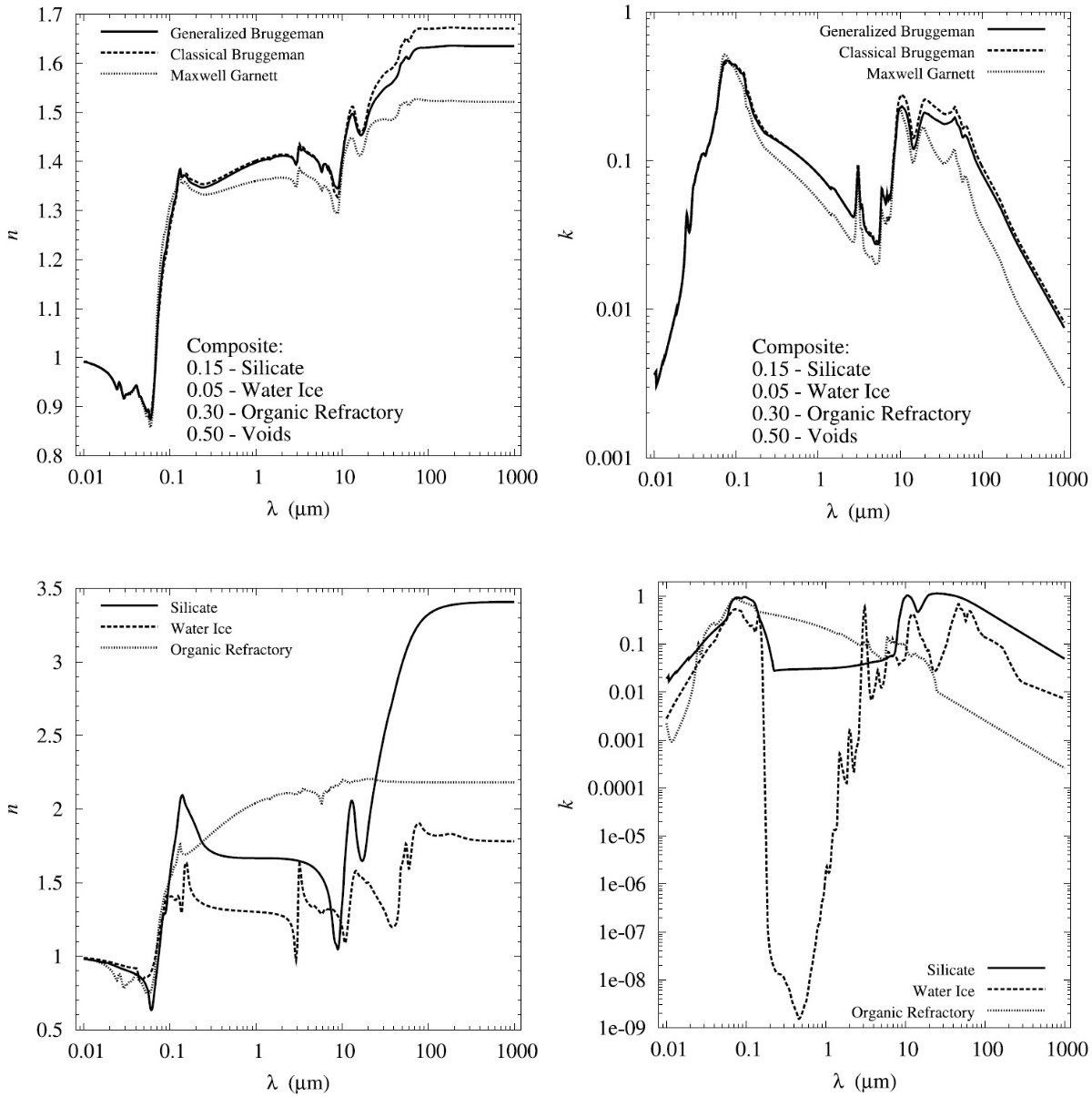
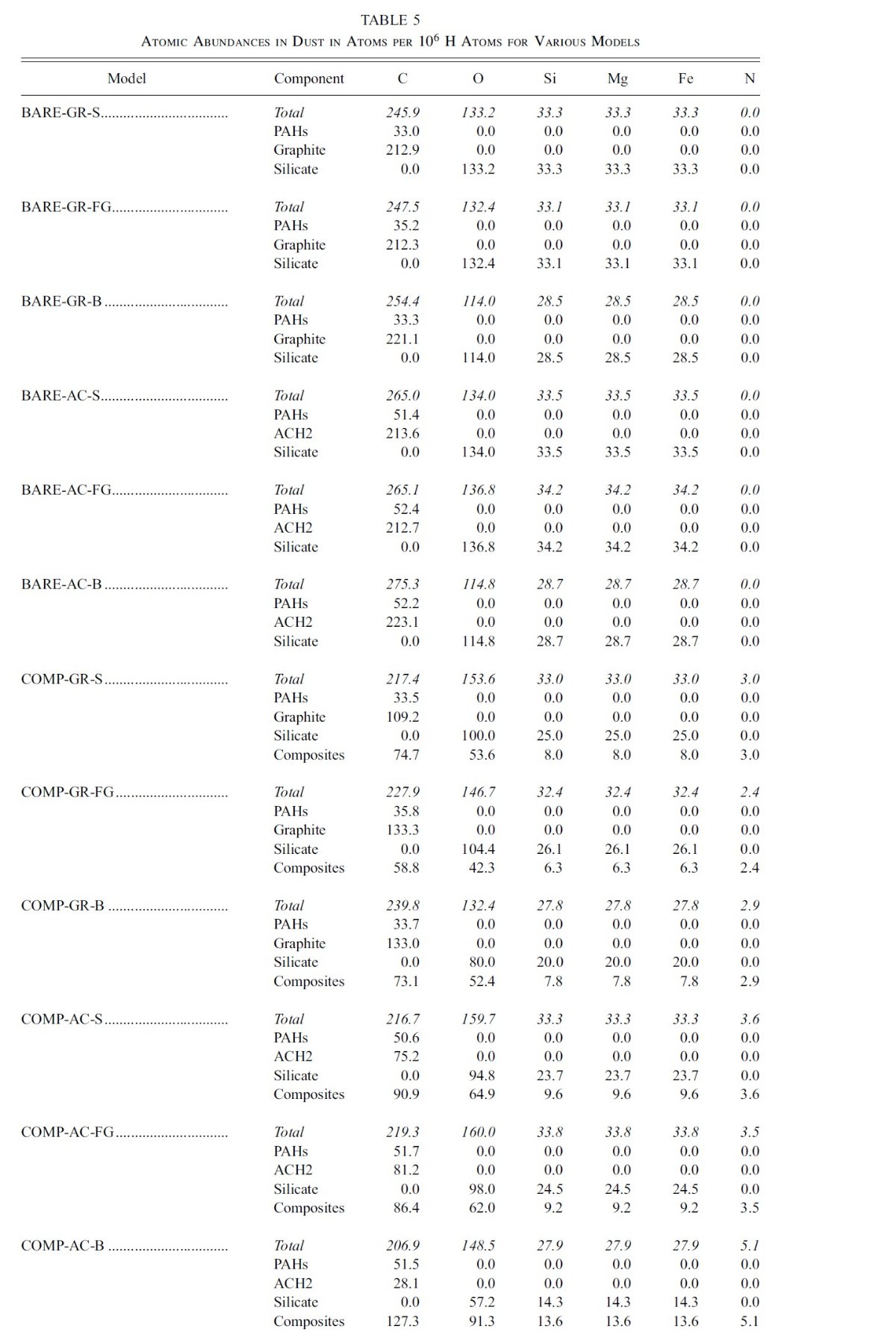
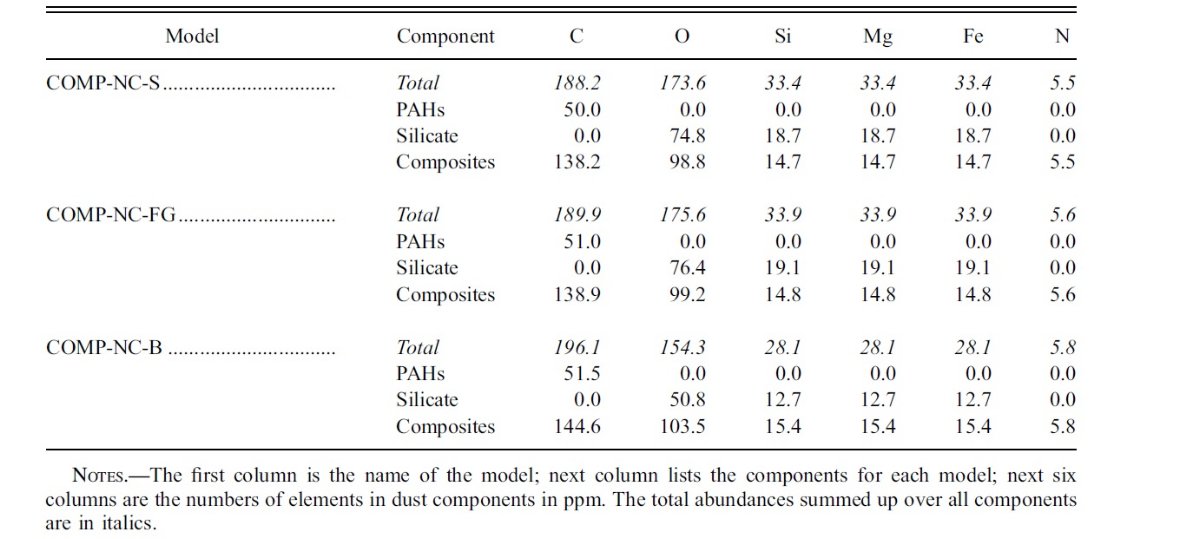
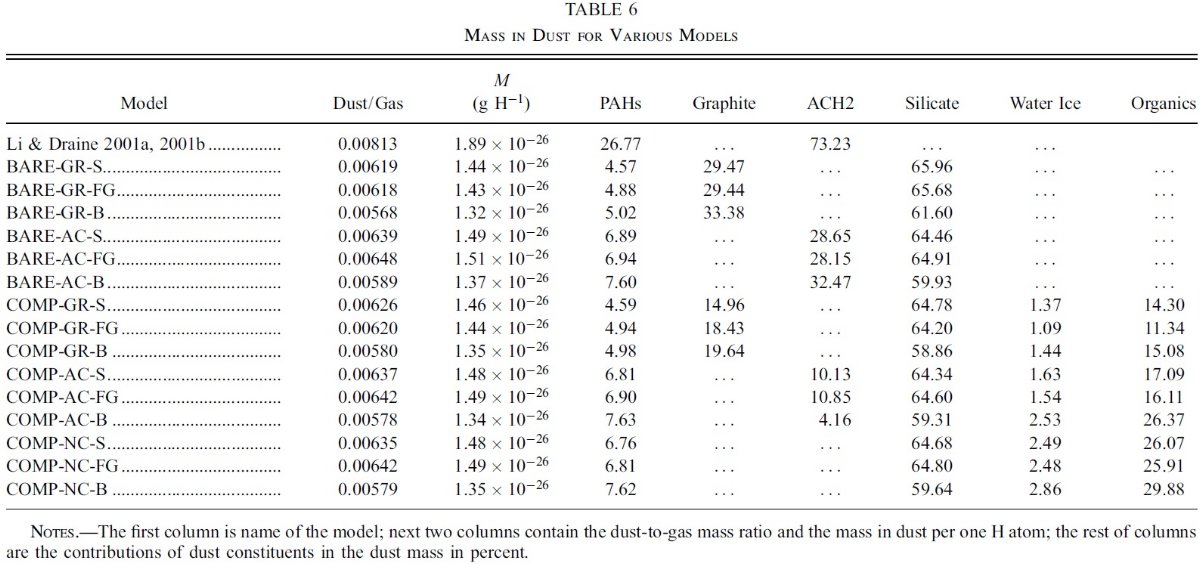
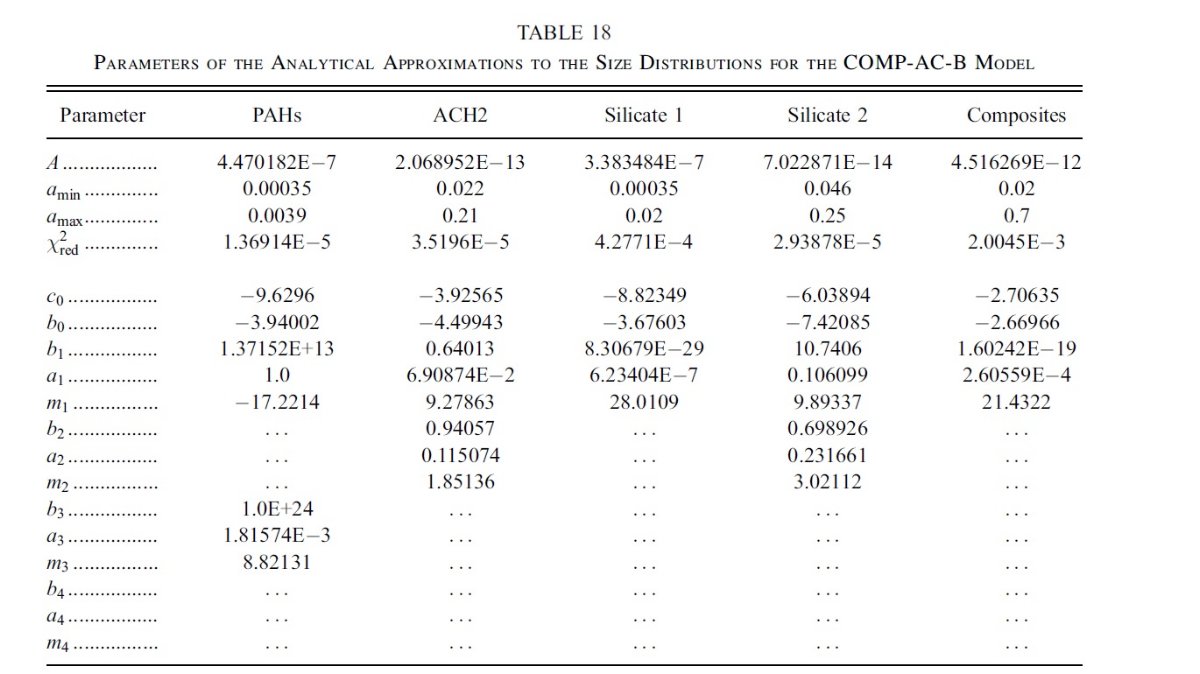
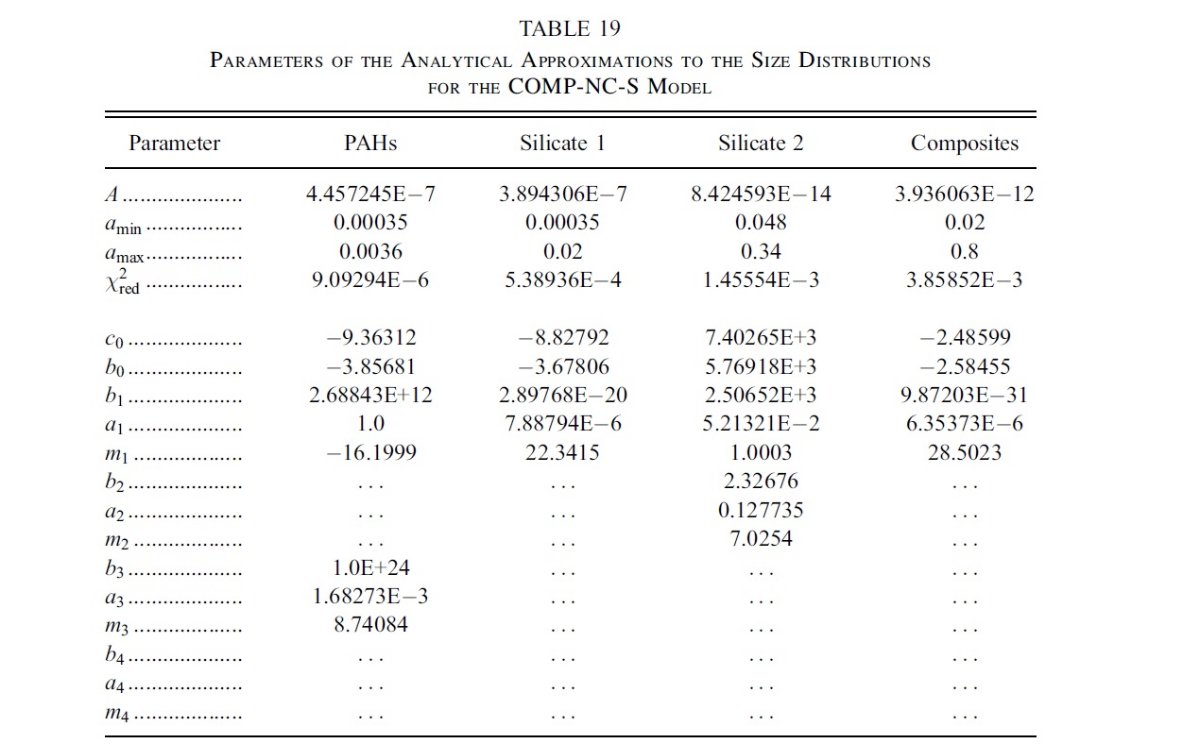
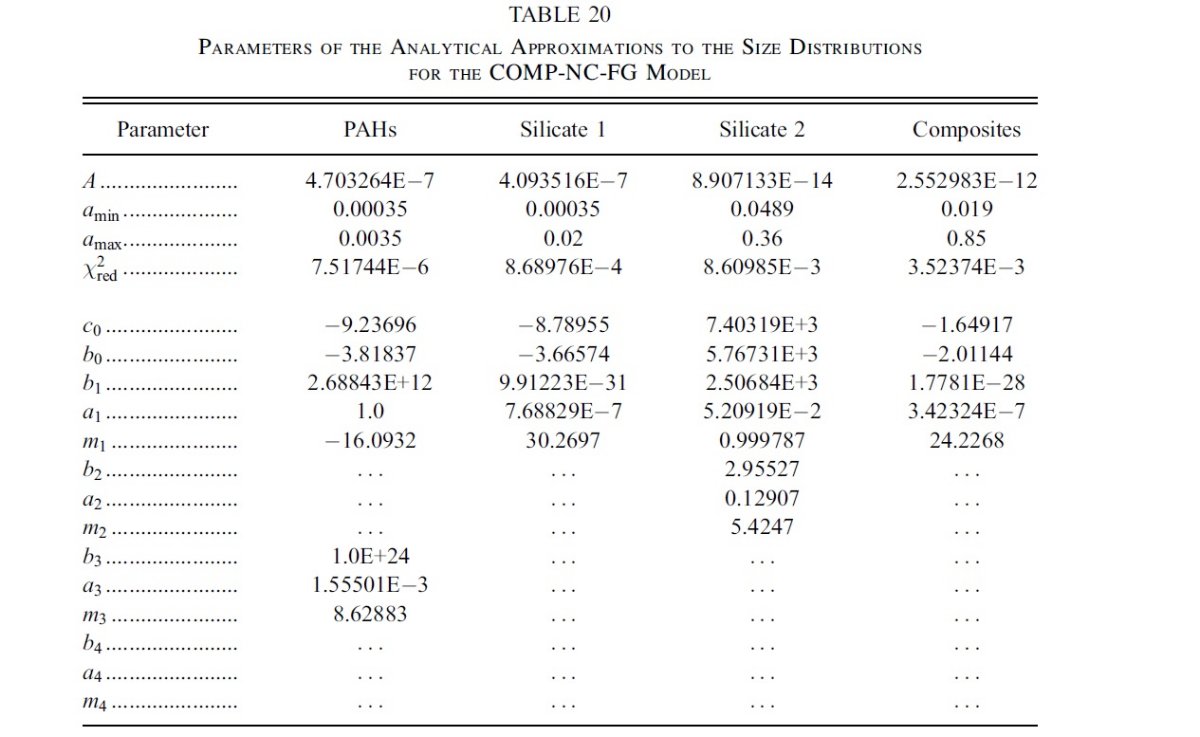
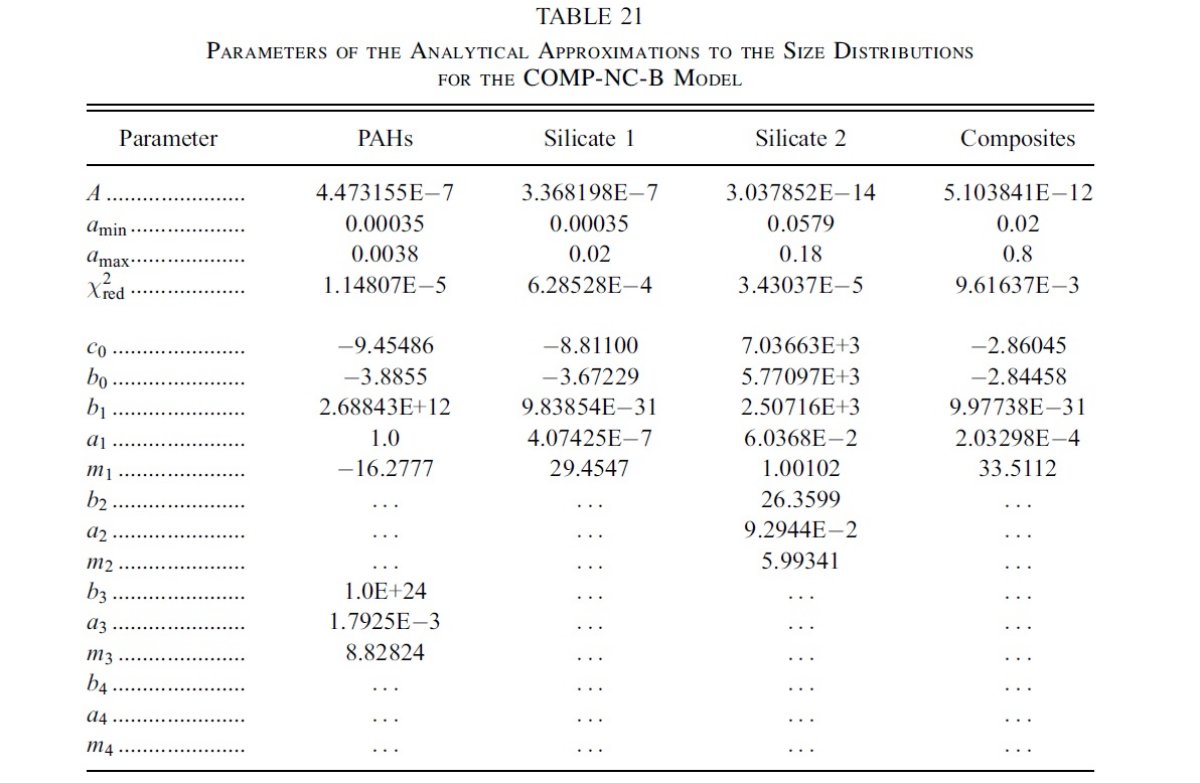
減光曲線 平均減光曲線には、Fitzpatrick 1999 を採用した。これは、 Cardelli et al. (1989) に較べ、R = 3.1 減光曲線の細かい特徴まで再現している。図１に減光曲線 を比較した。単位は τext/NH である。変換には Bohlin, Savagr, Drake 1978 による星間空間平均値、NH/E(B-V) = 5.8 1021 H cm-2 を使用した。 ダスト放射と元素組成 図２には、希薄星間空間からのダスト放射スペクトルを示す。図３と表１には 星の元素組成をダストモデルと比較した。 |
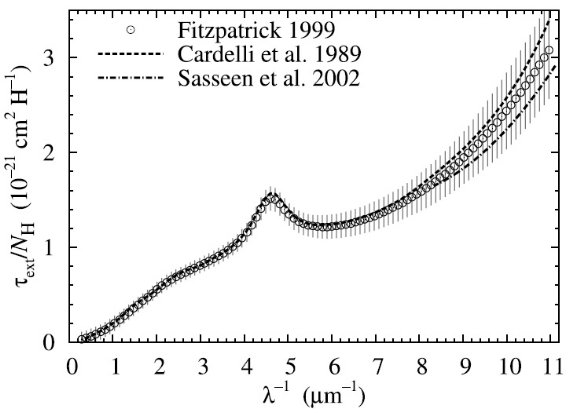
 図１．Fitzpatrick 1999 の R = 3.1 減光曲線。 Cardelli et al. (1989) および Sasseen et al 2002 の UV 減光も示す。 |
 図２．水素原子１個当たりの高銀緯 |b| ≥ 25 ダスト輻射強度。 データは DIRBE (Arendt et al 1998) と FIRAS (Dwek et al 1997) より。 |
 図３．Li-Dtaine 2001b ダストと星の元素存在比 (ppm) 比較。 |
|
（１）裸のシリケイトとグラファイト Draine, Lee (1984), Laor, Draine 1993, Weingartner, Draine 2001 の光学定数を使用する。 （２）ＰＡＨ 物質密度 2.24 g cm-3 を仮定し、吸収断面積には Li, Draine 2001b を使用する。 （３）非晶質炭素 ３種類の非晶質炭素、 ACAR, BE, ACH2 を試した。ACRE は Ar 雰囲気中で 炭素電極を放電させて作った。ACH2 は 10 mbar H2 雰囲気中で炭素電極を放電 させて作った。BE はベンゼンを通常の空気中で燃やして作った。Colangeli et al 1995. それらの光学定数は Zubko et al 1996b を使用した。 複合ダスト シリケイト、非晶質炭素、C25H25O5N の非揮発性有機物、水、空隙から成る。有機物の光学定数は Li,Greenberg 1997 から、水は Warren 1984 から採った。 PAH のサイズ分布 Li, Draine 2001b ではグラファイトの最小サイズを 50 A とし、PAH サイズ は 20A 以下として独立に扱った。非常に小さいグラファイトは簡単に言えば 脱水素化された PAH である。そこで、我々は PAH のサイズ分布はグラファイ トのそれの短い方の延長と考えた。 K(x, a) 計算に必要な量 K(x, a) を作るには減光断面積 Qexti(λ,a), 吸収断面積 Qabsi(λ,a), 放射率 Ei(λ,a), 密度 ρi, 質量割合 α ji を知る必要がある。密度等は表２に載せた。質量割合はダスト 構成から容易に計算できる。 |
有効媒質理論 (EMT) 裸のシリケイト、グラファイト、非晶質炭素の減光と吸収にはミー理論を行った。 複合物質に対しては、有効媒質理論 (EMT) により複素誘電率を求め、それを 使ってミー計算を行った。さらに、有効誘電率 εeff の 計算には Bruggeman 法に基づいて、形態ファクター (EMT-O) を入れた。 εk = 複合物質を作る k-番成分の誘電率 fk = 複合物質を作る k-番成分の体積比率 f1k = (5/9)fksin2(πfk) f2k = (2/9)fksin2(πfk) f3k = f2k f4k = fkcos2(πfk) Llk = { 0, 1/2. 1. 1/3} として、 有効誘電率 εeff は以下の式を満たす。
放射率 Ei(λ,a) 放射率 Ei(λ,a) の計算には thermal-discrete approximation (TDA) を Draine, Li 2001 の熱統計力学法に適用した。著者たちは 200 A 以下の、非常に小さく温度の急上昇を経験する粒子からの放射スペクトルを 計算するのに TDA が有効であることを示した。 星間空間輻射 星間空間の輻射強度 JIRSF(λ) には Mathis, Mezger, Panagia 1983 による太陽近傍での表式を採用した。それは、 JIRSF(λ) = JUV(λ) + Σ WjB(λ, Tj) + B(λ, Tb) ここに、JUV(λ) は希薄化率 10-14 の有効黒 体輻射、次は、W1 = 10-14, T1 = 7500 K, W2 = 10-13, T2 = 4000 K, W3 = 10-13, T3 = 3000 K で, 最後は宇宙背景輻射 Tb = 2.7 K である。 |
|
式８の解法 式（８）は１次のフレドホルム積分方程式である。その解法は ill-posed 逆変換問題の典型 (Tikhonov et al. 1995) である。解法としては、 規格化法 Press et al 1992, Tikhonov et al 1995, Backus-Gilbert 法 Backus, Gilbert 1970, エントロピー極大法 Narayan, Nityananda 1986 ] がある。我々は規格化法を採用した。 Default Solution の問題 星間減光と星間偏光を解くために、エントロピー極大法は、Kim, Martin, Hendry 1994, Kim, Martin 1994, 1995, 1996 により使われた。この方法は default solution をまず要求する。これはエントロピー最大法の安定解 を見つけるのに必要である。彼らは両端を区切ったべき乗則を使った。 しかし、我々のケースで default solution を 探し出すことは不可能である。 |
規格化法 Zubko, Krelowski, Wegner 1996a, 1998, Zubko (1997) は規格化法で星間減光と星周減光(R CrB 星)の両方をうまく解けることを示した。 数学的な詳細は Zubko (1997) に述べたので、ここでは概略を記す。これも省略にした。 |
４．１．ダストモデルの種類星間ダストは５種類星間ダストは次の５種類、（１）PAHs、 （２）グラファイト、（３）非晶質 炭素、（４）シリケイト、（５）複合物質、から成ると考えた。それらから、 次の組み合わせを考えた。 （１）裸のシリケイトとグラファイト。Li, Drine 2001b に同じ。 （２）PAHs, 裸のシリケイトとグラファイト, 複合粒子。 （３）と（４）は （１）と（２）の組み合わせ。ただグラファイトは非晶質炭素 （５）PAHs + 裸のシリケイト＋複合粒子 モデルの名付け規則 BARE = PAHs と裸の粒子 COMP = 複合モデルが付加 -GR = 裸の粒子がグラファイト -AC = 裸の粒子が非晶質炭素 -NC = 炭素なし -S = 太陽組成 -B = B 型星組成 -FG = F, G 型星組成 したがって、例えば BARE-GR-S は裸粒子がグラファイトで太陽組成を 仮定した BARE モデル。 |
４．２．計算の詳細データ波長点1/3.0 - 1/0.912 μm-1 の間を λ-1 で等 間隔に 100 分割した。さらに、DIRBE フィルターに対応して 3.5, 4.9, 12, 25, 60, 100, 140, 240 μm, 最後に、FIRAS の 160 - 1000 μm 間の 93 波長がデータ点である。 ダストサイズ ダストサイズは成分毎に 30 - 100 点を amin - amax 間を対数で等間隔に分割した。PAH, グラファイト、シリケイトの最小半径は 3.5 A とした。 複合粒子は amin = 100 - 500 A で結果に影響が少ないので、 amin = 200 A を使用した。全ての種類に対して、 amax = 5 μm とした。 |
|
図の説明 図４−１８にはモデルフィットの主な結果を示す。各図は次の４パネルから成る。 （１）各成分毎のグレインサイズ分布。 （２）計算減光曲線と各成分からの寄与。 （３）元素存在比 （４）モデル放射スペクトルと各成分からの寄与 サイズ分布がダブルピークの成分では減光と放射のグラフでは線の太さを変えて 別々に表示している。 グラファイト BARE モデル グラファイトグレインの入った BARE モデルでは、紫外/可視減光はグラファイト と PAH が寄与する。シリケイトは遠紫外を支配する。紫外のコブはグラファイトと PAH の双方が寄与する。放射では、PAH とグラファイトが 3 - 25 μm を支配し、 25 - 250 μm はグラファイト、λ > 250 μm ではグラファイトと シリケイトが半々である。 |
非晶質炭素 BARE モデル 非晶質炭素 BARE モデルでは、紫外・可視減光の大部分は非晶質炭素が担う。 遠紫外の向斜は小さなシリケイトグレインと PAH が受け持つ。紫外のコブは完全に PAH で作る。近赤外放射は PAHs とシリケイト、25 - 60 μm の放射は シリケイト、λ >: 60 μm は非晶質炭素である。 複合モデル COMP モデルでグラファイト、非晶質炭素が組み込まれたモデルはどちらも 対応する BARE モデルと似た点がある。しかし、複合成分は可視から遠紫外まで で主な寄与を成す。 3 - 60 μm の放射は BARE モデルと似ている。しかし、 複合成分は λ > 200 μm で寄与が大きい。 グラファイト、非晶質炭素が組み込まれていない COMP モデル グラファイト、非晶質炭素が組み込まれていない COMP モデルでは IR/opt/UV の減光と遠赤外放射は複合成分が主要となる。紫外のコブは PAHs が 受け持つ。これらのモデルは炭素の必要量が小さい。 |
|
炭素系粒子のサイズ分布は三つ山 図１９では、BARE-GR-S モデルのグレインサイズ分布を Li,Draine 2001b と 比較した。Li-Draine モデルでは炭素系粒子のサイズ分布は 5, 50, 3000 A の３つのピークを持つ。一方、我々のサイズ分布はグラファイトが 0.1 μm, PAH が 15 A で二つのピークになる。グラファイト成分は 非常に小さなサイズまで延び、脱水素化した PAH 種族を成している。 この脱水素化した PAH 種族が必要とされるのは、PAH の特性放射帯なしに 中間赤外の連続放射を作るために必要なのである。これは非常に小さい シリケイト粒子からの 10 μm 放射帯を被い隠す役割もしている。 Li, Draine 2001b のグラファイトサイズ分布の小さい側の端にある 50 A コブ も無構造の中間赤外連続放射を生み出すのに必要なのである。 |
シリケイト粒子のサイズ分布はべき乗 シリケイト粒子は Li-Draine でも BARE-GR-S モデルでもべき乗則の サイズ分布に従う。BARE-GR-S モデルの方が勾配が緩く、 MRN モデルに近い ので大きい粒子の割合が多い。Li-Draine モデルは分布則の関数形を決めて いるので、 COMP COMP モデルのフィットでは成分比率を変化させて差を最小にする。その結果 表３にあるような組成を得た。図２０には空隙率 0.50 の構成に対する 光学定数を示す。図には構成物質の光学定数も示した。 |
|
フィットは元素比制限に依存 表４にはモデルのズレを示す。表を見るとすぐわかるが、フィットの良さは 元素存在比の制限に大きく依存する。ズレが最小になるのは F-, G-型星の 存在比を課した時である。表に載せた非晶質炭素は ACH2 タイプで、 ACAR, BE タイプは許容範囲内のフィットが得られなかった。 |
どのモデルでもフィットできる 一般的に各ダスト構成で、減光と放射をフィットできた。定量的には 表４の不一致度が 10±2 以内に入ることに現れている。しかし、 元素存在比に関してはそうでない。COMP モデルは対応する BARE モデルと較べ、 不一致度 Φd が小さい。もちろん成分が一つ増えたの でそれ自身は当然である。表４を見ると、 B-型星組成で炭素量を抑えるのは 難しいことが判る。 |
５．３．１．ダスト量とサイズ分布COMP モデル中の水表５にはダストで消費される元素量を、表６にはダスト成分の質量を 載せた。COMP モデルは水分子を 5 - 21 ppm 必要とする。 Whittet et al 1997 の Cyg OB2 #12 方向観測は 2 ppm を示しているが、この値が希薄星間空間の 典型値かどうか分からない。一方、図２１は COMP モデルが 3.1, 6 μm 銀河中心方向星間吸収をうまく再現していることを示している。 サイズ分布の解析的表現 サイズ分布 f(a) (μm-1H-1) を f(a) = A g(a) と する。A は規格化定数。∫g(a)da = 1 である。g(a) を以下のように表す。 |
 表示式の項 この式は包括的表現なため多めの 14 個のパラメタ―を含む。式 20 で、 co + bo log a のべき乗項、カットオフ項 - bi |log(a/ai)|mi, ピーク項 -bi |a - ai|mi である。 カットオフとピークはサイズ分布をべき乗則からずらすために必要である。 表７−２１＝近似式パラメタ― 得られたパラメタ―は表７-２１に示す。 |
|
近赤外減光曲線の比較 図２１には色々な BARE, COMP モデルに対する近赤外減光曲線を示す。 観測点は Lutz et al. (1996) が銀河中心方向水素再結合線から求めた 2.5 - 9 μm 減光である。 一般的に言って、 COMP モデルの方が観測に近い。3 - 3.5 μm と 5.5 - 7 μm の構造は主に水の氷と不揮発性有機物による。 付加成分の必要性 図２１から直ちに分かることは付加成分の必要性である。つまり、 別のタイプのシリケイト、金属酸化物または硫化物、CO2 やメタン の氷などの追加か、あるいは現在使っている光学定数が悪いかである。 |
しかし、 ただし、それら新しい候補の光学定数は知られていない。また、 モデルが高銀緯の分子雲のように視線方向に存在する複数成分の天体 による減光をフィットしたのに対し、 銀河中心方向の減光がそれらと大きく異なる可能性もある。 図２２と図２３にはダストの散乱性質を比べた。図２２のアルベドは 平均減光断面積に対する平均散乱断面積の比、図２３の非対称パラメタ― は散乱角のコサインの平均値である。一般にモデルは観測より低い値を 与えている。その中では COMP モデルのフィットは BARE モデルより 良好である。 |
|
BARE モデルのサイズ分布 今回の研究で重要なことは、いくつかの種類のダストモデルが現在の 観測、減光、赤外放射、星間元素組成制限、を同時に満たしたという 点である。その一つは、 PAH, 裸のグラファイトとシリケイトグレインから 成る。元素組成制約を課すと、我々のモデルは Li, Draine 2001b と 似た量の PAH 分子とグラファイトを含むが、グラファイトサイズは もっと小さく、 PAH はもっと大きい。図１９を見よ。一方、 シリケイトのサイズ分布は MRN 分布に近いが L-, Draine 2001b モデル より勾配が緩い。また我々のシリケイトサイズ分布のピークは彼らより 低く、それが我々の Mg/H, Si/H, Fe/H がたった 33 ppm しかない理由である。 これに対し、 Li, Draine 2001b は 50 ppm を必要とする。 COMP モデル もう一つの種類は濃い分子雲中で想定されるような氷を含む複合ダスト を付加した。複合粒子のサイズは裸粒子より大きい。これは分子雲中で 氷や有機物が寄り集まるという形成シナリオと適合する。そのような 粒子が過酷な星間空間環境を生き延びることには、大きな粒子であるため 温度変動が小さい、内部を保護する表面層が形成される、揮発性物質自身が 非揮発性に変成する、等の理由が考えられる。 |
ＨＣモデル 第３の種類として、グラファイトが水素化非晶質炭素で置き換わったものが 考えられる。このモデルでは 2175 A コブは PAH のみで生み出される。 このようなモデルは星周空間でグラファイトのように高度に整列した構造が 形成されるとは考えにくいことから案出された。しかし、非晶質炭素を含む モデルは一般にグラファイトを含むモデルよりフィットが悪い。 しかし、それは非晶質炭素の光学定数が減光観測に最適化されていない ためかも知れない。「天体」グラファイトと「天体」シリケイトは Draine, Lee (1984) が MNR サイズ分布下で実験室データと減光観測をフィットするために 導いたものである。したがって、グラファイトを欠くモデルがフィットが悪く ても驚くべきではない。 炭素なしダストモデル 最後の種類は PAH と複合粒子内の有機物以外に炭素を全く含まない。 このモデルは、星間組成が B-型星と同じくらい低炭素量であった としても説明可能にするため、炭素を最小量で済ませたいという要求から 出てきた。COMP-NC-B モデルは C/H < 196 ppm である。このような モデルが可能になるのは Li, Draine 2001b の「天体」 PAH が 2175 A コブを再現するように調整されているからである。 |
|
１．BARE モデル PAH + ぐらふぁいと+ シリケイト、または PAH + 非晶炭素 + シリケイト、 の組み合わせは FUV から NIR までの減光、赤外放射、元素組成をよく 再現する。 COMP モデル BARE モデルに複合粒子を加えた。当然フィットは向上する。 COMP-GR-FG モデル フィットが最高なのは組成制限が F-, G-型星組成の場合である。 このモデルはアルベドと非対称パラメタ―も観測と良く合う。 |
星間空間組成はB-型星ではない？ B-型星組成の拘束を満足してフィットするのは難しい。したがって、 星間空間の組成は太陽か F-,G-型星組成なのであろう。 モデルに一意性はない モデルフィットの結果は、一意に決まるモデルが存在しないことを示す。 更なる拘束、例えば星間偏光、がモデル選択の幅を狭めるかも知れない。 X 線ハロー 小散乱角の X 線ハローがダストモデル間の優劣を決定するかも 知れない。Dwek et al 2004 は BARE モデルが大きな粒子の割合が高いので COMP モデルより良いと述べている。 |