Application of the Density-Wave Theory to the Spiral Structure of the Milky Way System

　アブストラクト　

　１．イントロダクション　

　２．ガスの系統的運動　

　２．１．一般論　

系統的運動とは　 　系統的運動と言う用語は平均円周運動に加わる、渦状重力場の結果生まれる 系統運動を指すものとする。この運動は、uθ1=円弧方向成分 と uω1=動径方向成分、を持つ。θ は太陽銀河中心線 から時計回りに測る。系統運動の大きさは 10 km/s 程度で回転速度の 250 km/s と比べると 1/10 程度である。 　系統運動が必要なわけ　 　腕のパターンスピードで動く座標系に乗った観測者を考える。この系では ガス運動は定常的で腕位置は一定である。図１の ABCD で囲まれた区間内の質量 流を考えよう。斜線部 EBFD は腕を表し、そこのガス密度は周囲の数倍高い。 腕が追尾型で、円周運動より遅い場合、もしガスが完全な円運動だと EB から入る 濃いガスは常に領域 ABCD の外側部に居ることになり、腕のパターンを維持で きない。腕部分には動径方向の流れが存在して、EB から流入したガスが FD を 通って流出するようにならなければいけない。同様に腕間空間のガスの動径運 動は銀河中心から離れる方向に流れないと定常波パターンが維持されない。 (うーん、つまり EA から入るガスは 少し上向きで、腕に当たり、腕からは少し上向きのガスが腕間ににじみ出て、 それで質量保存を成立させている？) 　系統運動の表式　 　腕の渦状重力ポテンシャル b を以下のようにする。 　　　b = A(ω)cos[2(Ωpt-θ)+Φ(ω)] 渦状パターンは -2θ + Φ(ω) = 一定で表される。ガス密度 σ, 系統運動 (uω1, uθ1) は、 　　　σ = D(ω)cos[2(Ωpt-θ)+Φ(ω)]　　　(1) 　　　uω1 = Uω1(ω)cos[2(Ω pt-θ)+Φ(ω)]　　　(2) 　　　uθ1 = Uθ1(ω)cos[2(Ω pt-θ)+Φ(ω)] 3つの物理量の大きさの間の関係は、　　　 D : uω1 : uθ1 : = (-kω) : m ( 1 - Ωp ) : k2 　　　　(3) σo ωΩ ωΩ Ω 2Ω2 ここで、σo＝ガス平均密度、Ω＝銀河回転角速度、 Ωp＝パターン角速度、m = 腕の本数、k＝2Ω[1+ (ω/2Ω)dΩ/dω]1/2 = エピサイクリック 振動数、で k = Φ'(ω) は局所動径方向波数である。追尾型腕、 つまり k < 0 で Ωp < Ω の時には、上式の 右項は全て正である。ｂとuθ1 の関係は、ガスの運動は 腕の外側縁で高速で、内側縁では低速になるという以前に得た結論を確認 している。

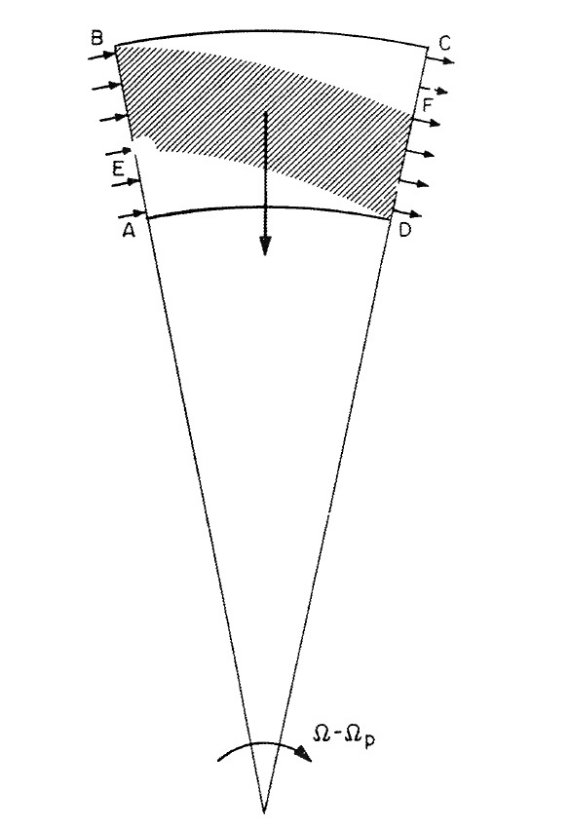
図１．ガスの腕 EBFD　の動径運動を示す図。AD と BC は完全な円弧。

　２．２．接線方向の系統運動：系統運動とミッシング水素　

回転曲線のコブの解釈　 　腕の接線方向のガス系統運動が最もはっきり現れるのは、図２に見える観測 回転曲線の振動である。振動が発見された早期には、この「窪み」は回転接点 部に中性水素が殆どないためと考えられ、真の回転曲線はピークをつないだ ものとされた。しかし、Shane, Bieger-Smith 1966 は、そうするとあり得ない ほど大きな密度比を腕と腕間空間に生むことを示した。彼らは、その不規則性 を、「腕に随伴する大規模運動の不規則性、例えば腕内ガスと腕間空間ガスと の間に存在する系統運動」によるものと考えた。Burton (1966) はサジタリウ ス腕の外側縁に沿う高速流の存在を注意した。ここで考えられている系統運動 は 10 km/s 程度の大きさである。 　密度波理論による説明　 　そのような運動の力学的性質が理解されるようになったのは Lin 1967 が 密度波理論を提唱してからである。腕の外側部で速く、内側部で遅い、という 運動は渦状構造に必然的に伴う特徴なのである。しかし、我々は動径運動にも 注意しなくてはいけない。 　回転曲線の「窪み」をどう説明するか？　 　回転曲線の「窪み」が腕の内側に対応するのか、腕間空間に対応するのか、 特にサジタリウス腕とノルマ・スキュータム腕の位置を決める際に、を知る ために、次のような疑問に答えなければならない。 (i) 接点円弧上での水素ガスの欠乏がそれらの窪みを生じるのに十分か、また その結果得られる腕と腕間空間のガス密度比は観測と比べ尤もらしい値か？ (ii) 系統運動は観測される回転曲線を説明するのに十分なのか？ このため、天の川銀河に合うモデル渦状腕からのラインプロファイルを作る。 これは観測プロファイルから渦状構造を導く通常の研究とは逆のプロセスで ある。 　水素輝度温度 Tb の基本式　 　スピン温度とガス分散速度が銀河内で一定という仮定で次の式を得る。 　　Tb(v,l) ∼ ∫ρ(r,l)exp{[v-V(r,l)]2/2c 2}dr ここに、v = 視線速度、r = 太陽からの距離、c = 乱流速度である。

図３．「ミッシング水素」がプロファイルの急な縁を動かす効果。太い実線＝ 一様密度。左：l=49 で腕を通過。右： l = 37 で腕間を通過。コントラストが 強まると、左はピークが高くなり、右は低くなる。 　水素欠乏モデルでは不十分　 　水素欠乏モデルでは不十分なことを示そう。二つのモデルを考える。 （i）完全な円周運動、例えばシュミットモデル、と一様密度を仮定する。後に このモデルを基本状態と呼んで引用する。 （ii）ガスは同じ円周運動を持つ。密度に第３章で述べる渦状構造を加える。 一つの腕から次の腕への密度変化はサイン関数型とする。 c = 8 km/s を仮定してプロファイル計算に進もう。 　二方向でモデルプロファイル計算　 　プロファイルを計算する方向の一つは円周接点が腕間空間にあり、もう一つは 腕上にあるとする。これは天の川では l = 37 で接点がサジタリウス腕とノルマ・ スキュータム腕の中間にある場合と、l = 49 で接点がサジタリウス腕上にある 場合に相当する。

図４．「系統運動」と「ミッシング水素」の効果の対比。「ミッシング水素」 では密度こんとらすと= 3:1 とした。 (i) サジタリウス腕の外側縁、l = 58°, (ii) サジタリウス腕の中央、l = 49°, (iii) サジタリウス腕の内側縁、l = 41°, (iv) サジタリウス腕とノルマ・スキュータム腕の間、l = 37° である。縦軸 スケールは任意である。 　(ii) モデルの密度コントラストとプロファイル　 　(i) の基本状態モデルに対するプロファイルは図３の太い実線で示されてい る。各プロファイルに見える急な縁だけが回転曲線を作るのに必要なので、 図ではその部分だけを拡大した。このモデルは (ii) モデルで密度コントラスト が 1:1 の場合に相当する。コントラストを上げていくと、視線方向が腕の上を 通るか、腕の間を通るかに従って、プロファイルのピークは次第に高くなるか、 低くなるかする。その様子は図３の細い実線で示される。プロファイルの急な縁 はそれに従って、右にずれたり、左に移ったりする。その結果、縁速度から決 まる回転曲線の形はシュミットモデルからずれていく。図３の特徴は (i) 縁の移動量は腕間空間の l = 37 の方が腕上 l = 49 より大きい。 (ii) 各プロファイルで移動量には密度コントラスト無限大に対応する上限がある。 その値は腕間空間 l = 37 の時 10 km/s, 腕上で 3 km/s である。 (iii) ピーク高さ比は密度コントラストと共に上がって行く。コントラスト 1:1 の時ピーク比 1.17:1, 3:1 では 1.89:1, 10:1 では 2.5:1 となる。コントラスト 無限大ではピーク比 2.7:1 である。 　「ミッシング水素」はズレに不十分　 　これ等の結果のみでも「ミッシング水素」を回転曲線の窪みの原因から排除 するに十分である。 l = 30 -70 で観測されるピーク比は最大 1.6:1 である。 これは密度コントラストに 3:1 の上限を与える。このように低いコントラスト では回転曲線の変化は 4 km/s で観測される 18 km/s よりずっと小さい。

図５．回転曲線の比較。回転速度をプロファイルの縁の半分の所で決めたので、 実際の値より 15 - 20 km/s 大きい。 　モデル (iii)　 　系統運動の効果を調べるために、モデル (iii) を考える。ここでは密度分布 は一様とする。しかし、視線速度 V(r, l) はモデル (ii) の渦状構造に対応 する系統速度が付与される。接線方向、動径方向の双方に振幅 8 km/s のサイ ン関数型系統運動を仮定する。それに対して理論プロファイルを l = 30 - 85 で計算した。初めの 2 モデルに対してもプロファイルを計算した。モデル (ii) では密度コントラストを 3:1 とした。 図４にその一部を示す。 (i) サジタリウス腕の外側縁、l = 58° (ii) サジタリウス腕の中央、l = 49° (iii) サジタリウス腕の内側縁、l = 41° (iv) サジタリウス腕とノルマ・スキュータム腕の間、l = 37° 各モデル毎のプロファイルから導いた回転曲線を図５に示す。太い実線はシュ ミット回転曲線である。細い破線は「ミッシング水素」による変化を、細い実 線が系統運動による変化を示す。太い破線は両方の効果を合わせたものである。 系統運動の腕接線方向成分が急縁線を右または左に直接 8 km/s 移すことは 図４のプロファイル変化から明らかである。この値は系統運動振幅に与えた ものと同じである。系統運動に伴うピーク高さの上昇、低下は観測と合う。 　「ミッシング水素」による誤差　 　図の５で、太い破線＝双方の効果が合わさった曲線を見ると、「ミッシング 水素」の効果は、小さいとはいえ、渦状腕の縁の位置を数百パーセク誤らせる ことが判る。例えば、図５で、腕の縁の位置はピーク A なのであるが、ピーク B をそう捉えてしまう危険がある。

　２．３．サジタリウス腕とノルマ・スキュータム腕　

遠距離と近距離の不定性　 　電波天文学者には周知の事実であるが、我々の銀河の太陽周円＝半径 10 kpc 以内の渦状構造を定める際の最大の問題は距離不定性である。つまり、ライン プロファイルから読み取られる質量密度を遠距離と近距離の二つにどう配分する かである。２１ cm プロファイルの銀経変化からはある程度の情報は得られるが、 特に接点付近では、この問題は完全な解決を見ていない。幸運なことに、系統 運動の接線方向成分の研究から得た結果を使えば、この問題を克服できる。 銀河面から離れた方向の観測データは要らない。太陽と「3 kpc 腕」の中間領域 では、接点円周状の渦状腕の位置は回転曲線上に観測される振動から直接に定め られる。この領域には二本の腕＝サジタリウス腕とノルマ・スキュータム腕、が 存在する。 　上がり＝ピークと下がり＝谷　 　そして、回転曲線の上がり＝ピークは腕の外側縁、下がり＝谷は内側縁に対 応する。図２でピークは l = 55° と 34° に起き、銀河中心距離 8.1 kpc と 5.5 kpc に対応する。谷は l = 42° と 25° に起き、銀河 中心距離 6.6 kpc と 4.2 kpc に対応する。「ミッシング水素」効果を考慮す るとサジタリウス腕は 6.8 - 8.3 kpc, ノルマ・スキュータム腕は 4.4 - 5.6 kpc が接点円周の半径である。同じ議論を南銀河の回転曲線に適用すると、 サジタリウス腕の接点円周は半径 7.0 - 9.0 kpc, ノルマ・スキュータム腕の 接点円周は半径 4.7 - 5.8 kpc となる。図６にはこれらの値に基づいた銀河 円盤状の配置を示す。 　腕の巾　 　腕の巾を定義しておかないと話しが先へ進まない。ここでは腕の巾＝二つの 連続する腕の間隔の半分で定義する。これは、渦状構造のポテンシャル動径方 向波長の半分と言っても良い。銀河の若い星が作る巾はこの定義より小さい。 Roberts 1969 の観測では、若い星の配置は銀河ショック＝腕の内側縁のすぐ 外側に並ぶ。この巾は彼の評価では動径方向波長の 1/8 である。天の川の場合 腕の巾は 1.6 kpc 程度なので、若い星の巾は 400 pc にあたる。我々がここで 使う「巾」は中性水素に対するものである。追尾型の渦状銀河では腕の幅は ピッチ角 i と、 　　　tan|i| = mλ/ωπ の関係にある。ここに、λ = 渦状パターンの動径波長＝腕巾の２倍、 (-i) = ピッチ角である。腕の幅は図６から直接測れ、ノルマ・スキュータム 腕で 1.2 kpc, サジタリウス腕では北銀河系での 1.5 kpc から南銀河系での 2.0 kpc まで変化するが、ここでは北銀河の値を使う。こうして、動径波長 はサジタリウス腕で 3.0 km, ノルマ・スキュータム腕で 2.4 kpc となる。 どちらもピッチ角 6° - 7° を意味する。

図６．回転曲線から導かれるサジタリウス腕とノルマ・スキュータム腕の位置 　ピッチ角　 　ピッチ角は図６を直接調べても得られる。サジタリウス腕の場合は先の 評価と大体同じだが、ノルマ・スキュータム腕の場合は図６で殆ど円弧状で ありピッチ角は非常に小さい。しかし、ノルマ・スキュータム腕が円弧状に 見えるとしても、もし全体が描かれた時には円ではないだろう。 円弧上に見えたとしてもそれは不規則性の一つと看做すべきである。 したがって、ピッチ角　6° - 7° は妥当と考える。

　２．４．動径方向系統運動　

　３．理論的渦状パターン：観測との比較　

分散関係の積分　 　密度波理論によると、回転曲線と質量分布が決まった銀河では、あとパターン 速度さえ決まれば渦状腕のパターンは決まってしまう。銀河系に対して質量分布 にシュミットモデルを仮定すると、パターン速度だけが残されたパラメタ―に なる。計算としては、仮定したパターン速度を用いて、単に Lin, Shu (1967) の図２を積分するだけである。幾つかの注意は、 (i) 銀河系は準定常状態に達しており、動径速度分散 ⟨cω ⟩ は以下の安定性臨界値に達している。 ⟨cω⟩ = 0.2857 ( 2πGσ ) 2 k2 ここに、σ = 星の表面質量密度である。 (ii) ガスの重力は無視する。 　図９にはパターン速度 Σp = 11.5 km/s/kpc の図を示す。 太陽近傍の rms 分散は以前の 52 km/s から 37 km/s へ低下した。 　密度波理論からの推奨値　 　これらの計算の結果、腕間距離がパターン速度に著しく依存することが 分かった。例えば太陽近傍では、 Σp = 11.5 km/s/kpc の場合に波長 = 3.3 kpc だが、 Σp = 20 km/s/kpc では 7.8 kpc となる。次節で見るよう に、波長 = 3.3 kpc なので可能なパターン速度は 11 - 13 km/s/kpc に制限 される。述べておくべきなのは、このパターン速度は密度波理論から "near resonance level" として推奨される値であるのみならず、星の移動 と渦状重力場に対するガスの反応からも満足できる値である。

図９．理論腕パターンと観測との比較。理論パターンは 1965 シュミットモ デルとパターン速度 11.5 km/s/kpc を仮定。斜線部＝回転曲線のデコボコ から導いたサジタリウス腕とノルマ・スキュータム腕。上図で 10 kpc 太陽 周円上側部に沿った点の列は局所腕。腕位置の一致はよい。パターンの開口 が速すぎることは 1965 シュミットモデルの 10 kpc より先での修正が必要 なことが判る。

　４．結論