2.1.流体力学モデル
仮定モデルに用いた仮定は Winters et al. 1994 を参照せよ。
2.2.輻射輸達モデル
これも Winters et al. 1994 に述べた。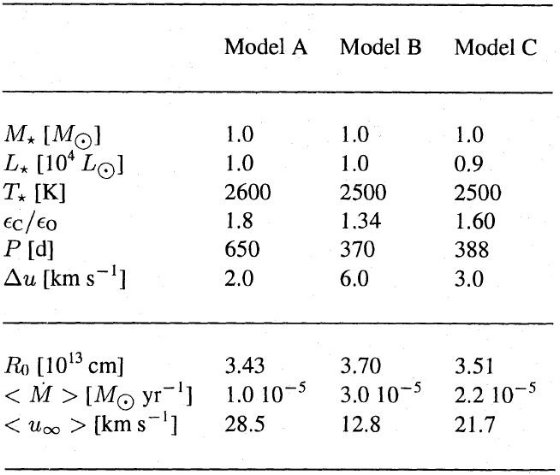
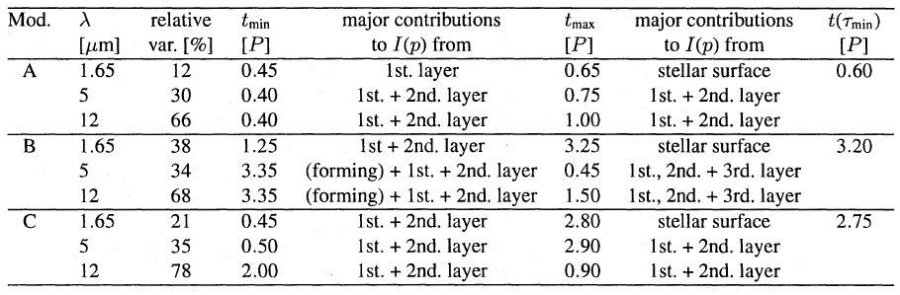
表1.モデルのパラメター。
アブストラクトダストシェルモデル長周期変光星ダストシェルモデルの輝度分布と空間スペクトル(?) を示す。ダストシェルの形成、振動数依存の輻射場と流体力学方程式を 結合して、ダストシェルモデルの空間輝度分布を導いた。 観測との比較 輝度分布は時間に依存する星半径の数倍のスケールの構造を持つ。この モデルと類似の構造が観測されている。その時間変化も観測結果と一致する。 モデル計算によれば、極大、極小の時期は波長により異なる。 1.イントロマスロスメカニズムマスロスメカニズムで一番有望なのは、(1)ショックエネルギー散逸により 大気の一部が上に浮かぶ、(2)そこにダストが出来て輻射圧で加速される。 という2段階説である。 |
SEDからダスト形成を導く Le Bertre 1988 炭素星の SED を色々な変光フェーズで調べ、ダスト形成が 6 R* 付近で起きる。 形成箇所が時間で動く。 Ridgeway, Keady 1988, Danchi et al. 1990 IRC+10216 で同様の現象。 Danchi et al. 1994 酸素型星でも同様。 分離ダスト層 しかし、上記研究で仮定された定常的なダスト構造は不十分で、脈動とダスト層 形成の動的仮定を考慮したモデルが必要である。そのようなモデルとして、 Fleischer et al 1992, 1995, Hofner et al 1995 がある。 Winters et al. 1994 は周期的なダスト層形成が変光曲線の形に大きな影響を与えることを示した。 ここでは、それら分離ダスト層が空間輝度分布に与える効果を調べる。 |
2.1.流体力学モデル仮定モデルに用いた仮定は Winters et al. 1994 を参照せよ。 2.2.輻射輸達モデルこれも Winters et al. 1994 に述べた。 |
 表1.モデルのパラメター。 |
3.1.ダストシェルモデルの半径に沿った構造モデルA,Bは論文II と同じである。モデルCは異なり、マスロス炭素星 の観測パラメターに合うように取った。図1にはモデルA, B, C の異なる フェーズでの構造が示されている。内側境界で速度 v = Δv sin P で 与えている。図1の内容は(上)実線=速度v、破線=凝結度 fC (下)実線=K3、破線=温度 T fCの変化に現れているように、ダストの分布は非一様で、玉ねぎの 皮上に分かれている。また、温度分布はダストが集結している半径で階段状の 段差を作る。新しく出来たダストが外向き輻射を遮る結果、内側でのダスト形成は 抑制される。 3.2.モデルの時間変化モデルの違いモデルAでは各周期毎に新しいダスト層が 2 - 4 R* 付近に出来る。 一方、モデルBではモデル層が作られるのは4周期ごとである。モデルC の場合、新しいダスト層はほぼ3周期毎に出来るが、詳しい様子は完全 な繰り返しではない。モデル間の差が生じる原因は、脈動、ダストのκ メカニズムの非線形相互作用の結果である。詳細な解析は今後の論文で 扱う。 |
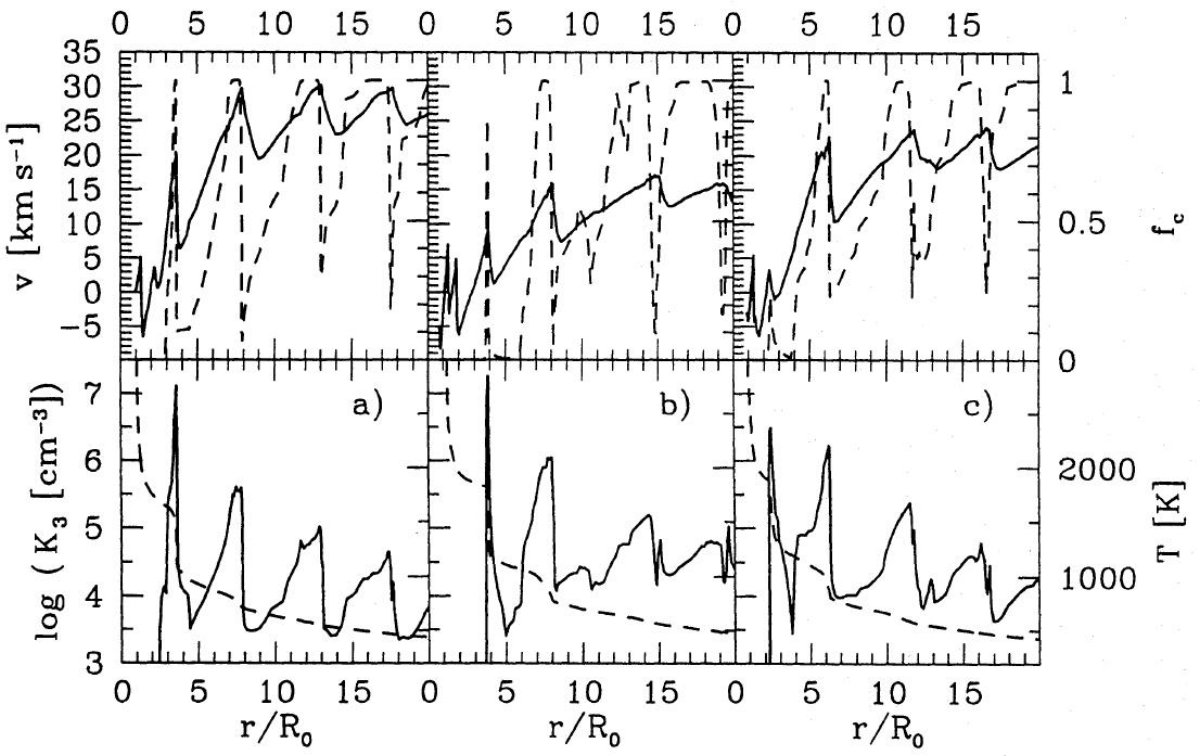
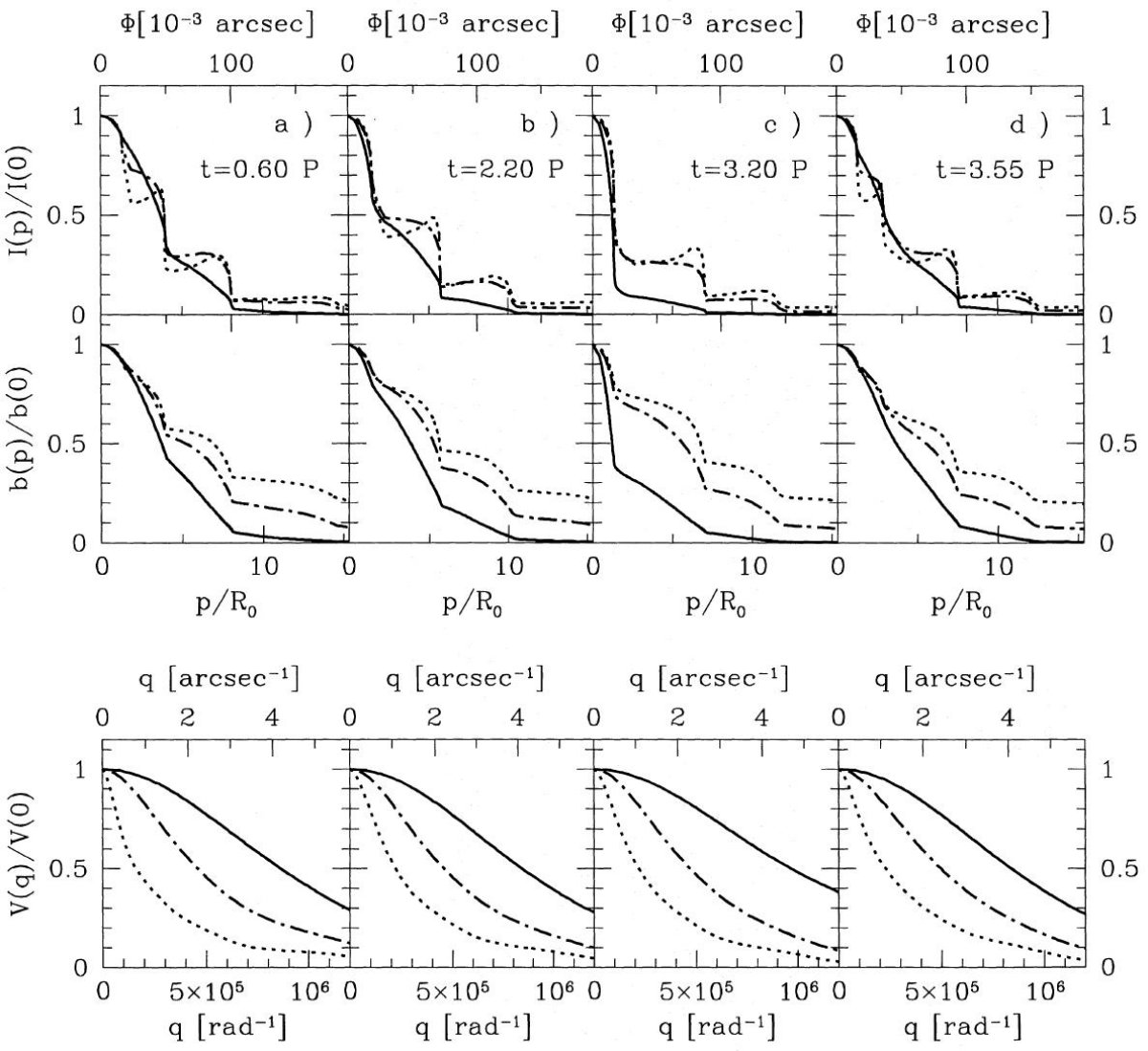
変光曲線と光学的深さの時間変化 図2には2波長の変光曲線と光学的深さの時間変化を示した。下段の 光学的深さの時間変化を見ると、新しいダスト層の形成により、脈動 周期の 0.1 くらいの間に光学的深さが急上昇する事が判る。このダスト層 形成はモデルAでは P = 0.7, モデルBでは P = 3.5, モデルCで P = 3 付近で起きている。ダスト層形成はどのモデルでも変光極小期に相当して いる。特にモデルB,Cでは深い極小に当たっている。 モデルB,Cではダスト層形成の間にも光学的深さが変動的な動きを示す。 この中間的変動はショック波によりダスト形成層における密度が周期的に 増減するためである。密度が上がるとダスト成長が加速され、すると凝集率 fC が上がりその結果光学的深さが増加すると言う過程が起きる。 ダスト凝集率の飽和 ダスト凝集率 fC が飽和すると、ショックの通過は単にダスト 層を外側に押しやり、光学的深さを単調に減少させるだけとなる。この 現象はモデルBでは P = 1.5 - 3.2, モデルCでは P = 1.5 - 2.7 で起きて いる。 変光曲線の副構造 論文II ではモデルAのダスト形成が変光曲線に構造を産み出すメカニ ズムを詳しく説明した。そこでは、 AFGL1062, AFGL1085, AFGL1235, R Lep, R Scl, の変光曲線副構造(Le Bertre 1992)はこの効果では ないかと述べた。しかし、他のメカニズム、ショックエネルギーの散逸、 二次ショックの形成、なども提案されている。どちらがよいか決着は 付いていないが、以下に述べる空間構造の検出は我々のモデルに有利である。 |
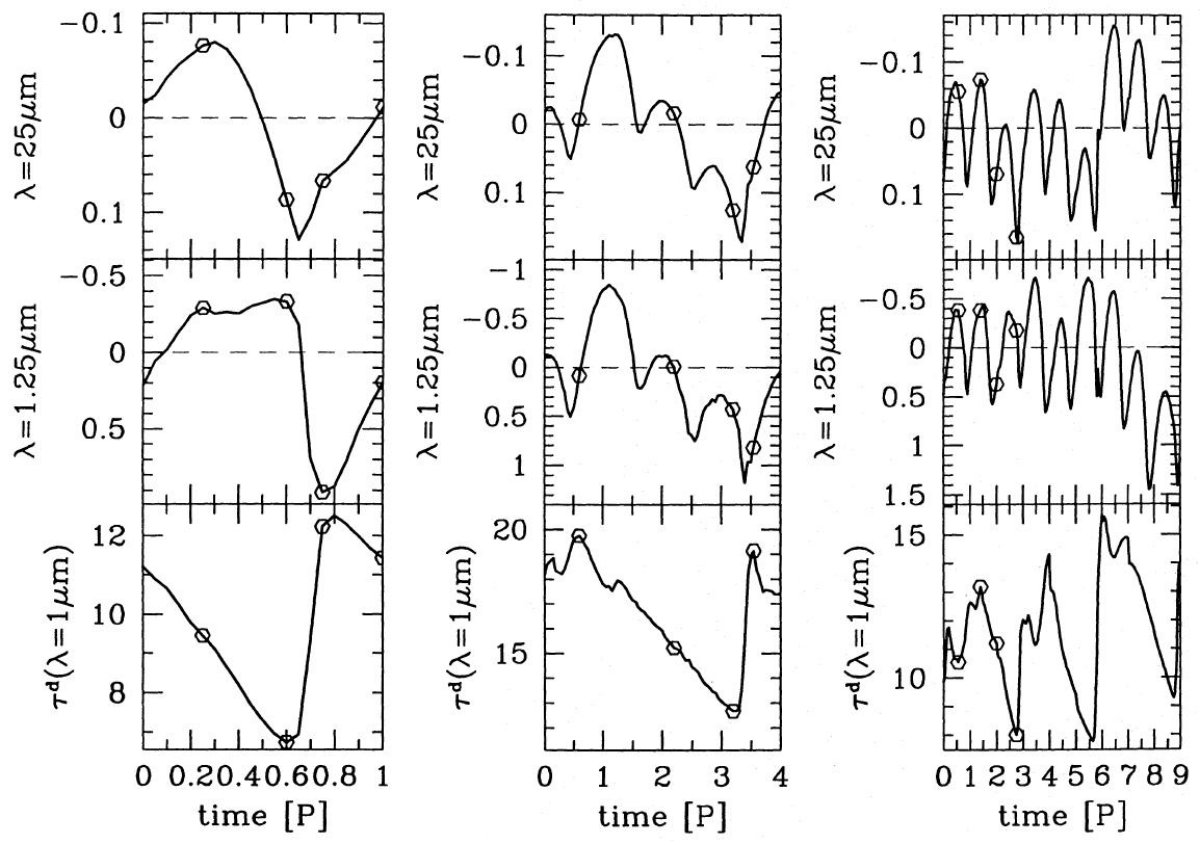
3.3.空間輝度分布輝度分布図3(モデルA)、図4(モデルB)、図5(モデルC)には、 輝度分布 I(p)、積分輝度分布 b(p)、ヴィジビリティ V(q) が色々な 波長とフェーズの組み合わせに対して示されている。選んだフェイズ は図2上に示されている。ダスト層間の間隔は数 R*, 1014 cm、程度である。これは 200 pc で 0.01 arcsec に相当する。地上 望遠鏡でこの間隔を分解するのは難しい。しかし、月の掩蔽を利用 すればミリ秒角(Richini 1989)を達成する事が可能である。その 際に得られるのは月の進行と垂直な方向に積分した輝度プロファイル b(p) である。図の中段にはそれを示した。 掩蔽観測可能な天体は限られており、干渉計が重要な手法となる。 その場合のヴィジビリティを下段に示した。 3.3.1.モデルA図に取ったフェイズP = 0.25 ダスト層は発達しきって、単に膨張していくだけ。 P = 0.60 新しいダスト層形成の直前。光学的深さは最小。 P = 0.75 ダスト層が発達し、光学的深さは最大。 P = 1.00 ダストグレインは成長を続けているが、膨張が勝って光学的深さは 減少。 ヴィジビリティの時間変化 1.65 μm 輝度分布(実線)には最内側層しか見えない。従って、 1.65 μm の等級変化は最内側層の力学進化を反映する。長波長に なると外側ダスト層が寄与してくる。5 μm、12 μm では その結果、輝度分布に段差が生じ、干渉計のヴィジビリティの時間 変化は q = 106 で 12%(1.65μm)、30%(5μm)、66% (12μm)が検出されるだろう。ヴィジビリティ極小(見かけ半径極大) は P = 0.45(1.65μm)、より長波長では P = 0.40 である。 見かけ半径の時間変化 1.65μm で広がりが最大になる P = 0.45 は最内側ダスト層における ダストの成長は停止した時である。5, 12 μm ではその外側ダスト層から の輻射も寄与が大きい。 P = 0.40 はすぐ外側ダスト層が 4.5 R* に達し、 中間赤外で寄与が大きい時期である。 図3b の上図を見ると、 P = 0.60 で広がり極小の時には 1.65 μm で見えるのは星の表面の広がりである。一方 P = 0.75 (5 μm)、 P = 1.00 (12 μm) の極小時には 3 R* の新しく形成された最内側 ダスト層が見えている。 |
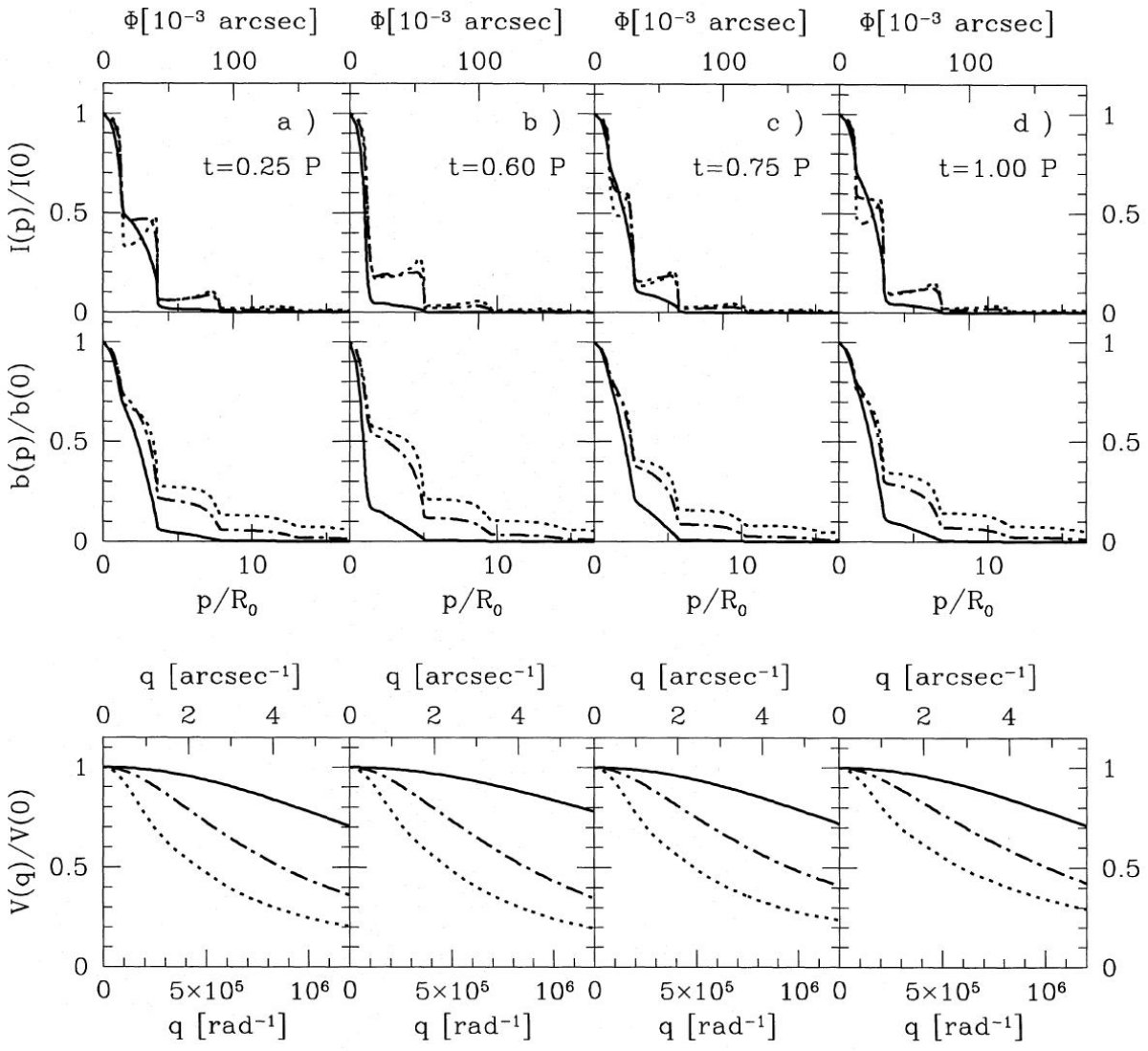
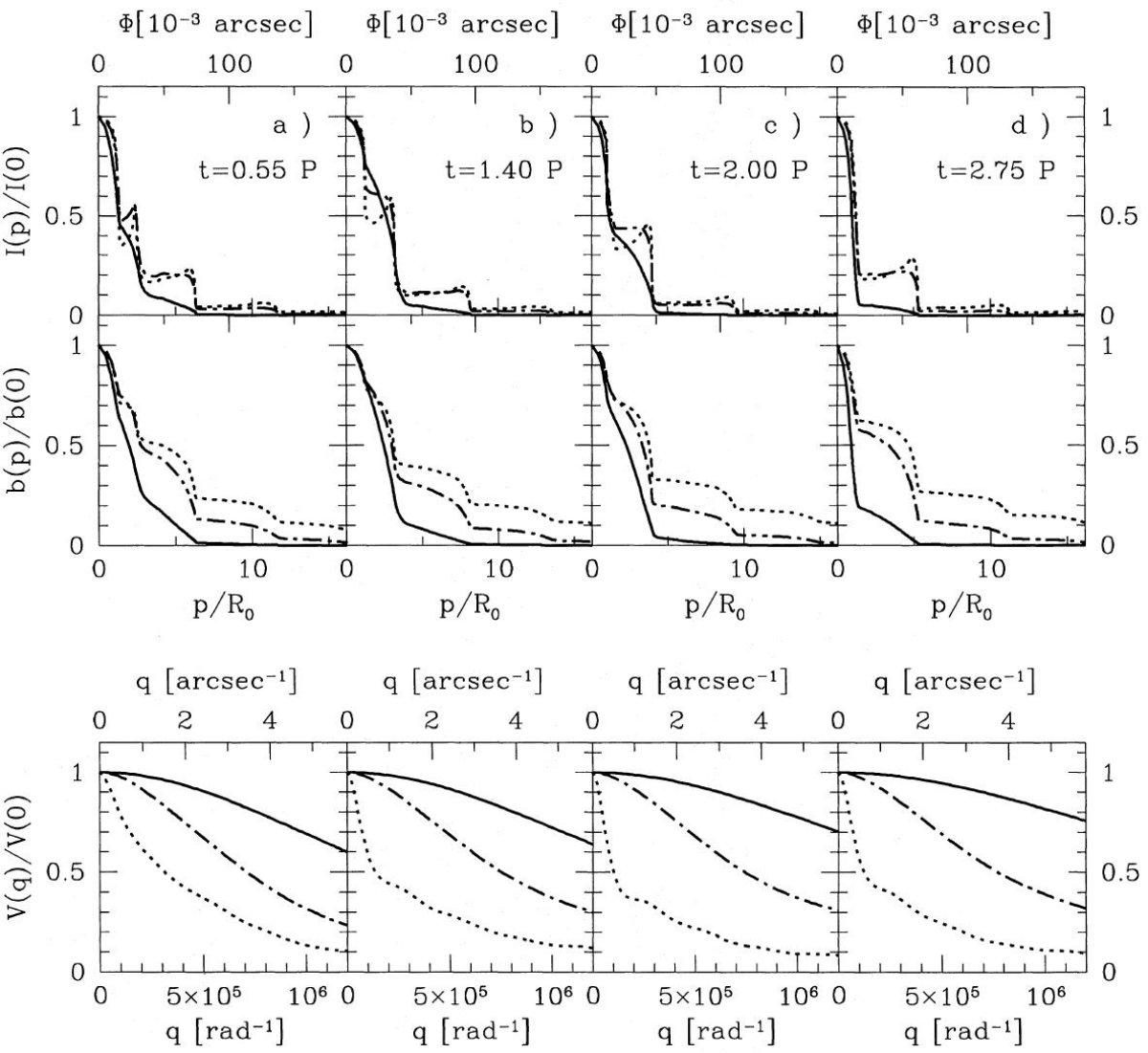
3.3.2.モデルB図に取ったフェイズP = 0.60 ダスト層が発達し、光学的深さは最大。 P = 2.22 ダスト層は発達しきって、単に膨張していくだけ。 P = 3.20 新しいダスト層形成の直前。光学的深さは最小。 P = 3.55 新しいダストの形成開始。光学的深さは第1中間極大。 ダスト層の広がり この多重周期モデルでは放射領域はモデルAよりずっと広がっている。 モデルBはモデルAの3倍マスロスが大きく、光学的深さも大きい。 その結果、外側ダスト層からの寄与が増している。 (環状積分輝度にしたらもっと 強調されるよな。5 μm でも結構いけそう。すばるで中心星像は消す 必要あるか? ) 光学的深さの時間変化 光学的深さが最小となるのは、最内側ダスト層が広がり切り、次の ダスト層形成が開始される直前である。この時、1.65 μm 見かけ ダストシェルの大きさは最小となる。5, 12 μm では P = 0.45(5μm), P = 1.50 (12μm) の第2ダスト層形成途中で最小の広がりとなる。 3.3.3.モデルC図に取ったフェイズP = 0.55 光学的深さの中間極小。 P = 1.40 ダスト層が発達し、光学的深さは最大。 P = 2.00 ダスト層は発達しきって、膨張の結果、光学的深さは減少。 P = 2.75 新しいダスト層形成の直前。光学的深さは最小。 マスロス率 モデルCのマスロスはAとBの中間である。このため、輝度分布の 段差もCほど強くない。時間変化に関し、A、Cと異なるのはその 不規則性である。そのような、モデル間の差は基本的には計算で 使用した炭素組成の大きさによる。マスロスの強さには依存しない。 ( ここのところは意味が不明。) |
|
ヴィジビリティの変動 ヴィジビリティの変動は多くの文献で報告されてきた。例えば、 McCarthy et al 1980 は IRC+10216 の 5 μm ヴィジビリティが 光度極大と極小とで 30 % 変化すると述べている。この変化は通常 ダストシェル内側半径が周期的に動くことを意味していると考えら れてきた。Danchi et al 1990, 1994 はダスト形成が光度極小付近 で起きると考えた。これは我々の計算結果と一致する。IRC+10216 の 構造が1年程度のタイムスケールで変化する事実を Ridgeway, Keady 1988 は光度極大付近でダスト破壊が生じる結果と解釈した。Danchi et al 1994 では13個の晩期型星が 11 μm で 5 年間に渡り観測さ れた。多くの星でヴィジビリティの変動が検出され、極小時の ダスト形成として解釈された。特に ο Ceti ではヴィジビリティ がフェイズのみでは決まらない、つまりダスト形成がサイクル毎に起きて いないことが判った。これは我々のモデルB,Cと合う結果である。 空間構造 炭素星、CIT 5, CIT 6, IRC+10216, でも O-リッチ星, VY CMa, NML Cyg, ο Cet, α Ori, NML Tau、でも空間スペクトル中に内部 構造が検出されている。これらは通常仮定されるべき乗則のような連続的な 物質分布では説明不能である。 我々のモデルでは階段状の輝度分布により、長波長(λ > 10 μm) ではヴィジビリティ関数に細かい構造が生じる。 IRC+10216 の場合 Ridgeway, Keady 1988 には IRC+10216 ヴィジビリティ関数, 1.65, 2.2, 3.15, 10 μm に著しいさざ波構造が見られる。彼らはそれから 一次元輝度変化への再構成を行い、典型的スケール 0.1 秒角の明瞭な 階段構造を導いた。これまで、信頼できる説明は提案されていない。 図6を見ると、IRC+10216 ダストシェルの広がりが波長により大きく 変化する事が判る。この振る舞いは Dyke et al 1984 によると他の天体にも 見出される。 最近 Richichi et al 1993 (private com.) はIRC+10216 の月掩蔽観測 1.65 μm から 0.002 秒角の分解能で一次元像再構成を行い、極めて 規則的な 0.03 秒角のステップ構造を検出した。もし、中央ピークの FWHM = 0.045 秒角を星像直径と考えると、階段の中心距離、 31.4 mas, 57 mas, 86 mas は中心距離 1.4 R*, 2.5 R*, 3.8 R* に 対応する。この結果に基づく解析は将来の論文で述べる。 モデルAと IRC+10216 の比較 上の階段位置 1.4, 2.5, 3.8 R* をモデルAと較べると P = 0.25 1.4, 3.6, 7.9 R* P = 0.60 1.6, 5.1, 9.6 R* P = 0.75 1.5, 2.7, 5.7 R* P = 1.00 1.2, 3.0, 6.8 R* モデルAのステップ間隔は IRC+10216 の観測値よりも広いようである。 ずれは外側ダスト層の方へ行くほど大きくなるようだ。これは、 モデルAでは R = 5 R* で 20 km/s に達するのに、観測された値は 15 km/s と小さく、しかもそれに達するのは 20 R* であることを 考慮すると無理もない。つまりモデルダスト層は実際より速い速度で 膨張している。加速が大きいのでダスト層間隔は外側ほど大きくなる。 それにも拘らず、モデルと観測の段差はファクター2−3の範囲で一致 している。 |
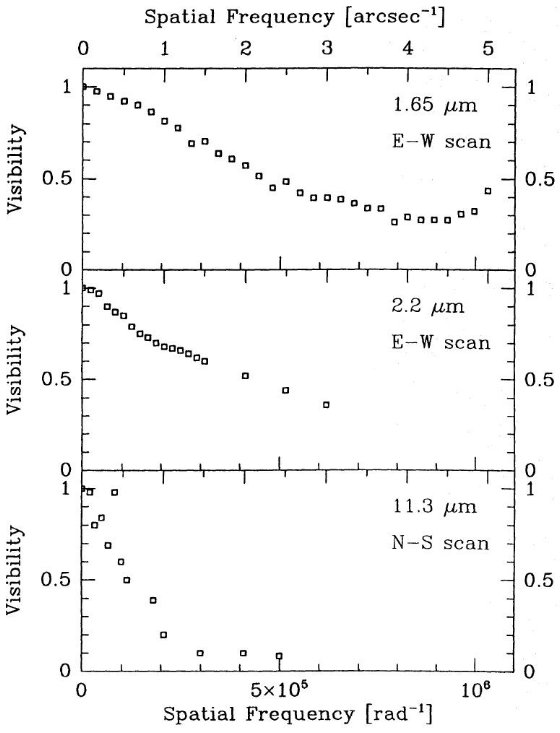 図6.IRC+10216 ヴィジビリティ関数 (Ridgeway, Keady 1988) 単波長で段差が見える モデルでは段差が現れるのは λ > 3 μm であるのに、 観測では 1.65 μm で早くも段差が現れる。同様に、モデルヴィジビリティ は 10 μm 以上で内部構造が見えてくるが、観測は 1.65 μm で もう見える。 ダストオパシティ シェル構造の見え方に決定的なのはダストオパシティである。今回 のモデルでは Maron 1990 の非晶質炭素のデータを用い、波長依存は 大体 λ-1 である。問題は論文 II でも 既に上昇途中での中間極大が観測より低いという形で現れていた。 炭素星SEDフィットでは λ-1.3 が示唆 (Jura 1983, Le Bertre 1987, 1988)されている。また、Winters 1994 でも近赤外カラーが観測からずれている。これらはオパシティの 形を純粋に非晶質 λ-1 と結晶質 λ-2 の中間を取る必要性を示している。 |
|
計算モデルの目的 この論文で用いた計算は個々の星の観測結果を説明するための 物ではない。むしろ、現象の背後に存在する物理メカニズムを 探るためのものである。 輝度分布の構造 観測された輝度分布に現れた構造は分離したダスト層が原因である ことが示された。空間スペクトルの時間変化も定性的にはモデルと 一致する。 |
有望 モデルと観測結果との比較から我々の方法が大変有望である事を 物語っている。 |