Circumstellar Dust Shells arpund Long-Period Variables II. Theoretical Light Curves of C-Stars

　２．モデルの方法　

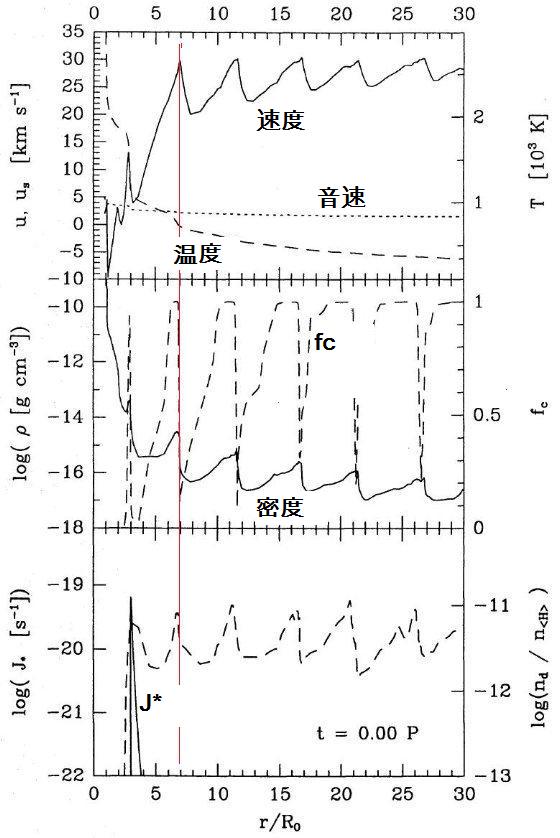
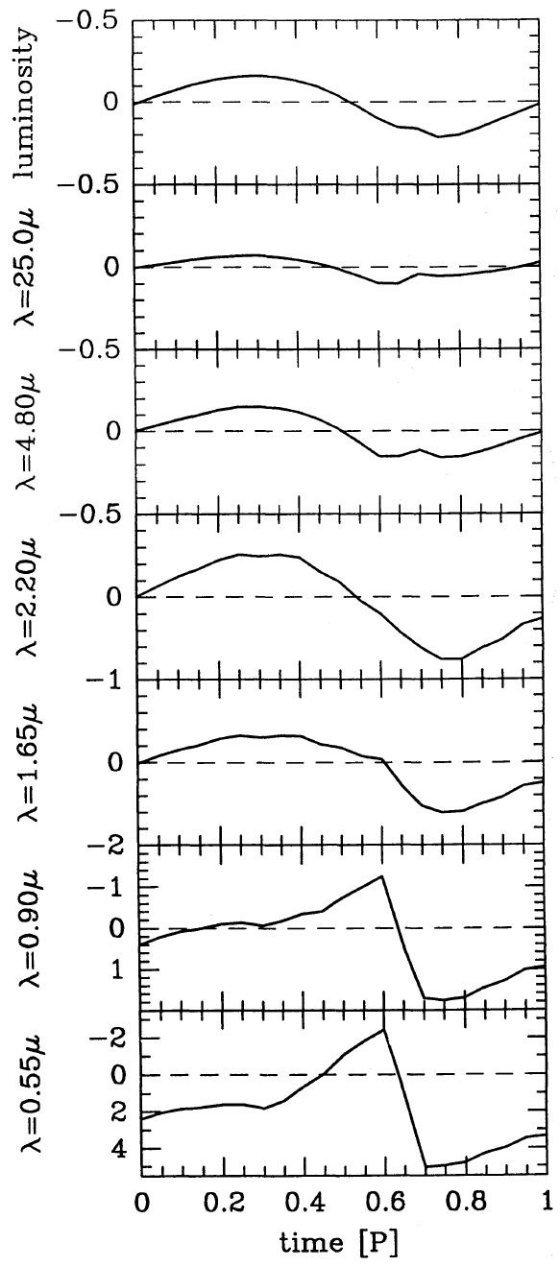
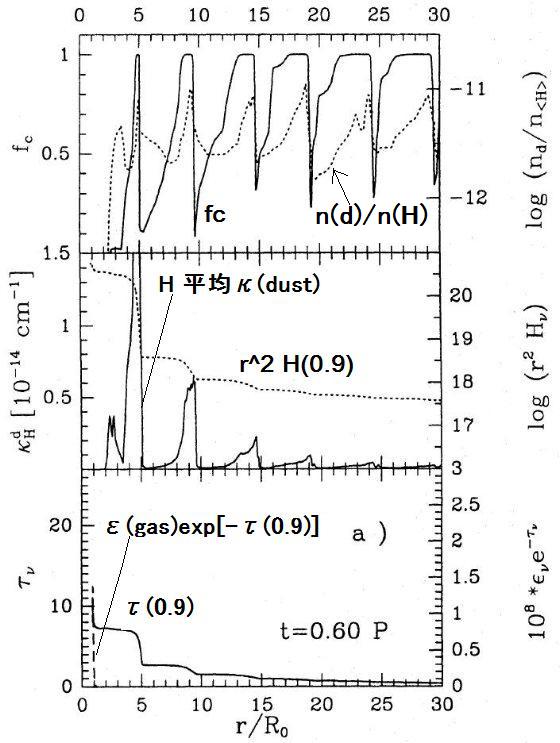
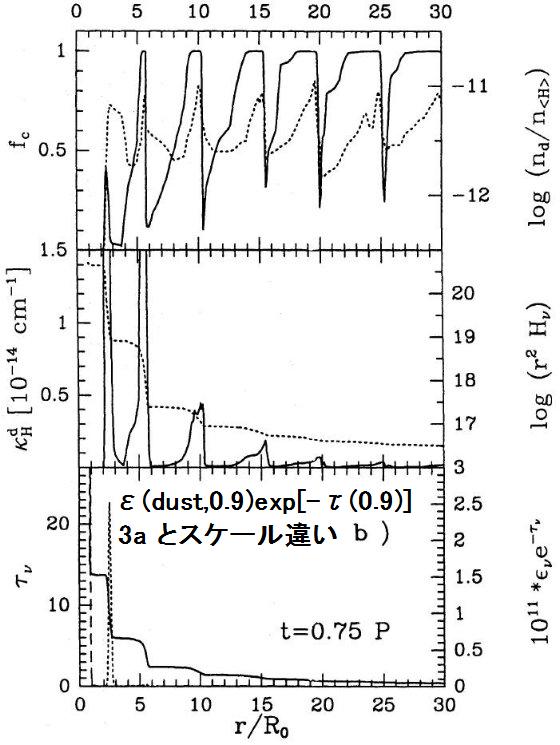
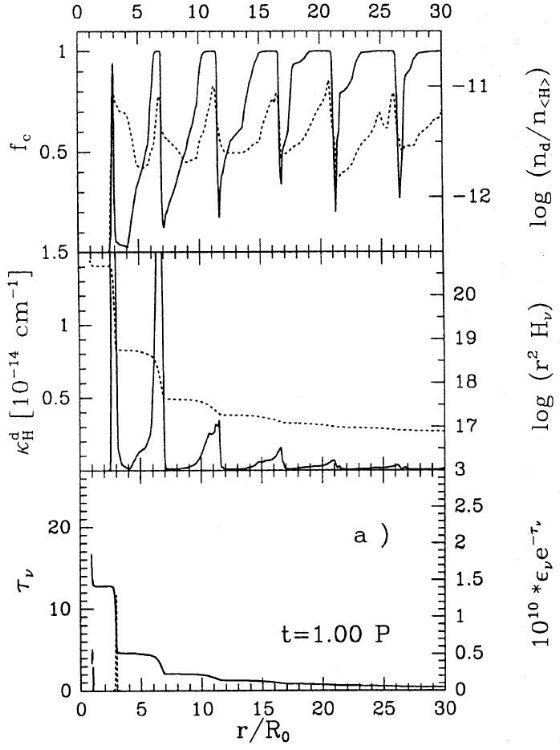
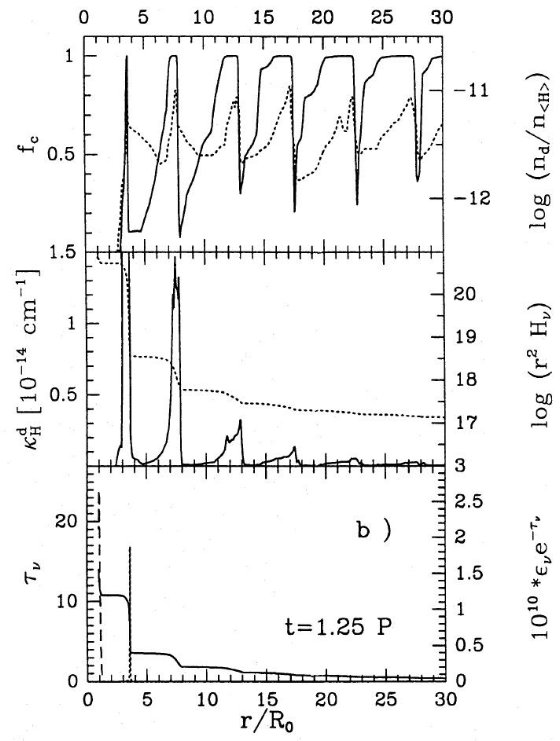
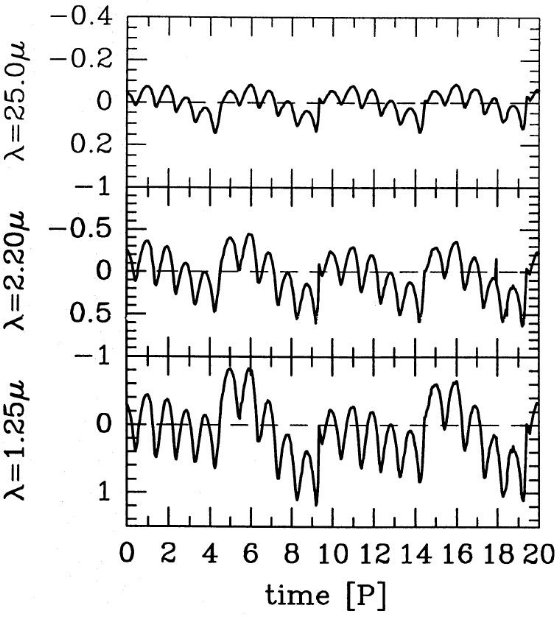
２．１．流体力学計算　 　等温ショック　 　計算式はラグランジュ座標で書かれ、 Richtmyer, Morton 1967 の エクスプリシット積分法で解かれた。ショックフロント背面の冷却は 瞬時に行われる、すなわち等温という極限ケース（Fleischer, Gauger, Seldmayr 1992 論文１）を仮定した。ショック後の冷却を考慮すると 計算は複雑化する。しかし、変光カーブの特徴は周期的なダスト層の 形成が原因で、その点に関しては両者の与える結果に大きな差はない だろう。 　ダスト形成　 　炭素以外は太陽組成、炭素組成 εC はフリー パラメターとした。H, H2, C, C2, C2H, C2H2 の化学平衡を解いて、 ダストの形成、蒸発や破砕による消滅を追跡した 　ダストシェルの構造　 　Lucy 1971, 1976 による輻射輸達の解法を用いてダストシェル各点での 局所平衡温度を決めた。等温ショックを仮定しているので、ガスとダスト の温度は等しい。 　内側境界条件とモデルパタメター　 　内側境界では速度を巾 Δu、周期 P のサイン関数型で与える。 モデルを規定するパラメターは T*, L*, M*, εi, Δu、P である。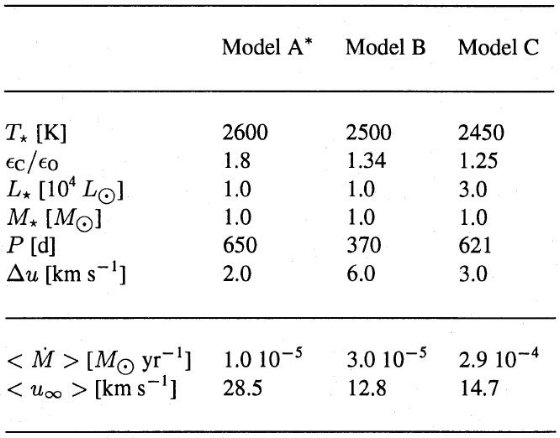 表１．初期の静水平衡モデルのパラメター。 最終モデルの時間平均質量放出率と最終流出速度も与えた。 (PLR によるチェック ) Ita, Matsunaga 2011 より、炭素星の輻射等級を見積もると、 (log P = 2.8, Mbol = -6、L=20,000 Lo), (log370=2.57, Mbol = -5, L=8000 Lo) なので、一律 10,000 Lo は ちょっと疑問。

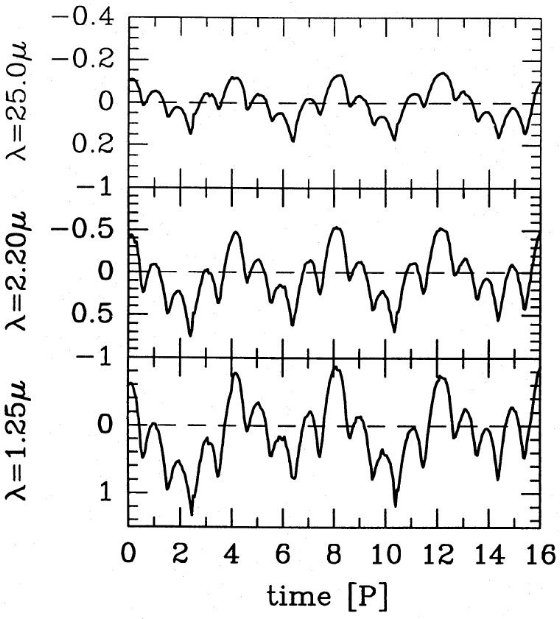
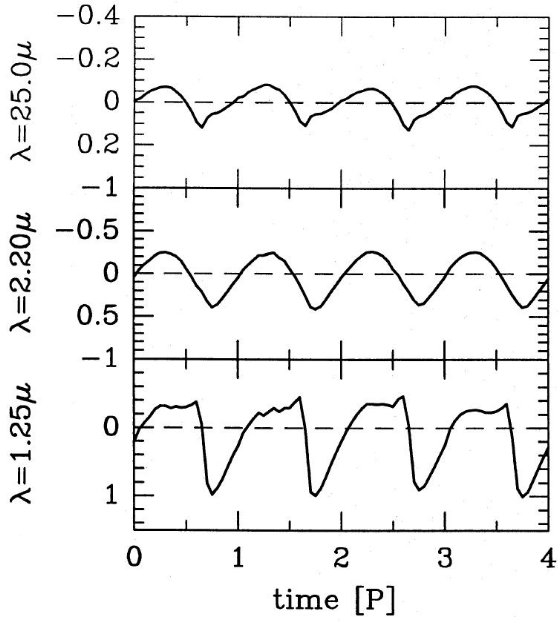
２．２．輻射輸達計算　 　輻射の計算　 　輻射の計算は波長依存の球対称定常輻射輸達の式を解いた。 解法は単一波長のモーメント方程式（変動エディントンファクター） と単一波長の光線に沿った光線強度に対する偏微分方程式の形式解 との逐次近似で行った。内側境界では輻射の拡散近似を採用し、 L*/16π2 （？）のフラックスが大気に 流入し、外側境界条件は r = Rmax で外側からの 輻射はゼロという仮定を置く。 　オパシティ　 　ガスは κg/ρ = 2 10-4 cm2 g-1 (Bowen 1988) の灰色吸収と放射を行うとする。この値は 想定される温度密度領域でのロスランド平均ガスオパシティである。ダストに 対しては小粒径近似を適用する。 吸収係数 κνd は 減光係数 χνd と等しく以下の式で与えられる (Gail et al 1984) κνd(r) = 8π2α0 3 Im { m(ν)2-1 } K3(r) = χνd(r) λ m(ν)2+2 複素屈折率 m は純粋な非晶質炭素の値Maron1990を使用した。 K3 はサイズ分布 f(a, r) の３次のモーメントである： 　a03 = ∫al ∞a3f(a,r)da 放射率 εν はガスとダストの和として、 　εν(r) = ενg(r) + ενd(r) = κgB ν(T(r)) + κνdBν(T(r)) 　ダストによる輻射加速　 　K3 は単位体積(cm3) 当たりのダストに取り込まれた 原子数である。fC = 凝縮可能な物質のどの割合が実際に凝縮して いるか、との関係は以下で与えられる。 　fC = K3/(εC - εO) ここで、全ての O 原子は CO と仮定している。すると、表面重力を単位とした 輻射加速は、 α = κH L* ρ 4πcG M* で与えられる。ここに　κH はフラックス平均減光係数である。 α は fC に比例する事が明らかである。

　３．結果　

計算パラメターは表１に載せた。 Claussen 1987 は周期に関係なく 10,000 Lo であることを示したので これを採用した。R Scl は C/O = 1.34, T=3000K, P=370 d が得られて いて、モデルＢはそれを採用した。IRC+10216 は P = 600 d である。 モデル計算から導かれた諸関係には必ずしも従わず、主に観測値を採用した。 　３．１．ダストシェルの構造　 　モデルＡの構造例　 　図１は流体力学的サイクル開始時 t = 0.00P でのシェル構造を示す。ダストの 分布がはっきりした層構造を示す事に注意してほしい。もう一つ、温度 の段差が幾つか見えるが、ダスト形成のスパイクに対応している。 これらは論文１で詳述されているので、ここではざっとまとめる。 　層構造の形成過程　 (1). R = 3 - 4 Ro でダスト形成。 (2). 脈動で圧縮され、ダスト成長が進む。fc = 1 に達して終了。 (3). ダスト加速により、速度場に急な構造ができ、ショックが発生する。 (4). ダスト層が不透明になると内側の温度が上がり、ダスト形成に影響する。 図１．t = 0.00P におけるモデルＡの構造 上：実線＝速度。点線＝音速。破線＝温度。 (温度一定なのに音速一定に ならないのはなぜ？) 中：実線＝密度。破線＝ダスト凝集度 fc. 下：J* =ダスト核形成率=毎秒、水素原子１個当たり発生するダスト数。 破線＝ダスト数/水素原子数。 ( P = 0 で最内側膨張開始、 P=0.25 で膨張の頂点、P=0.5 が出発点まで戻る。P=0.75 収縮しきった。 光度Ｌは膨張頂点で極大、収縮点で極小という仮定らしい。光球カラー または温度は？)

３．２．　モデルＡの変光曲線　 　波長別の時間変化　 　図２には 0.55 - 25 μm に対し、一周期の変化を示した。 境界条件として(2.1.には書いてなかったが)光度 L もサイン関数型の 変化を示す（図２最上段）。λ > 2.2 μm での光度曲線 の特徴は狭い第２極大が見えることである。一方、短波長側では 内側境界での変化はフェイズ 0.6*P 付近に出現する強いピークによって 完全に変形を受けている。このピークは長波長側での第２極大に 対応している。 　図３，４の内容説明　 　図３，４には幾つかの位相における物理量の動径変化を示す。グラフに 示されるのは、 上段：実線＝凝集率 fc。破線＝ダスト数密度/Ｈ密度。 中段：実線＝フラックス平均吸収係数。 　　破線＝エディントン フラックス H(0.9μm)。 下段：実線＝τ(0.9μm)。 　　短破線＝0.9μm での有効ダスト放射率 ενde-τ(0.9μm)。 　　長破線＝0.9μm での有効ガス放射率 ενge-τ(0.9μm)。 　3a : P = 0.6 　 　P = 0.6 はダスト形成開始直後である。ダスト層は全て完全に成熟 fc = 1 している。総ダスト光学深さは極小値 τ(0.9μm) = 7.23 である。この時 短波長フラックスは最大値に達する。図２を見よ。光学的深さが比較的浅いので 短波長フラックスの大部分は光球からのガス放射である。 (ダストの減光の殆どは散乱でなく吸収 と書いてある。 τ(0.9μm) = 7.23 で光球が見えるのか？ 中段 H を見ると、正にその強い、この星のフェイズとしては弱い、減光を受けた 光球を見ている。) 　P = 0.6 : 新しいダスト層の成長　 　3a 図（P=0.6）の nd/nH を見ると、3Ro 付近で上昇 していて、新しいダスト層が出来始めていることが見て取れる。この時点では まだこのダスト層の粒径は小さく光学的深さは小さい。 P = 0.7 になると、 新しいダスト層の τ が十分に大きくなって、光球からの光が吸収される 様になる。この時点で短波長変光曲線は極小となり、長波長では浅い中間 ピークが出現する。 　短波長フラックスへの寄与は主に最内側ダストシェル前面からの熱輻射へと移る。 寄与密度 ενexp(-τν) で、図３a と b とに縦軸スケールの差がある事に注意。 (図３ｂで点線＝ダストと破線＝ガスの どちらが支配的かは積分量が見てとれない。テキストではダストの方が効くという ことなのか？ ) 　P = 0.75 : 新しいダスト層の成熟　 　長波長では吸収が弱いため、この新しいシェルからの放射のフラックスへの寄与 が大きく、このフェイズでの中間ピークの原因となる。P = 0.75 では新しい ダスト層での凝集率 fc = 0.41 に達する。このダスト層の光学厚みは Δ τ0.9 = 7.75 である。 　P = 0.75 - 1.25 : 最内側ダスト層の放射　 　　P = 0.75 から P = 1 にかけて、光学厚みは最大値 Δτ0.9 = 8.40 に達するが、fc = 1 になるのは P = 1.25 まで待たなければならない。 これは膨張による密度、光学厚み低下の効果と吸着によるダスト成長効果との 競い合いの結果である。 　この時期、外側のダスト層は単に膨張して光学厚みを薄くしていくのみである。 その結果、ダストシェルからの単波長放射は最内側ダスト層全面からのダスト 熱放射が支配的になる。 P = 1.35 - 1.6 : 光球の放射　 　P = 1.35、τ0.9 = 9.70 でこの状況が変わる。最内側 ダスト層は膨張の結果光学厚みを減らし、この時点で Δτ 0.9 = 6.50 に落ち、同時に温度も低下する。その結果、光球 からのガス放射光が再びダスト層からの寄与を上まわるようになる。短波長 変光曲線は P = 1.6 極大に向けて上昇を開始する。P=1.60 ではダストシェル 全体の光学深さは τ0.9 = 7, 最内側層の寄与分は Δ τ(0.9)=4.37 である。 ( Te=光球温度、Td=最内側ダストの温度、 D=最内側ダスト層の光学的厚み、最内側ダスト層全面での垂直方向の光球寄与 ＝B(Te,0.9)exp(-D)、最内側ダスト層寄与はB(Td)。 だから、ここでの主導権交替のシナリオは Te, Td, D により結構微妙に変わる と思う。Te, D はある程度分かるとすると多波長モニター観測から　D を評価 できる可能性がある。)

図２．モデルＡの理論光度曲線。縦軸スケールは波長により変化している。 　二つのフェイズ　 最内側層に着目すると異なる二つのフェイズが存在する： 　　(i) 　P = 0.6 - 1.0 : ダストの形成と成長 　　(ii) P = 1.2 - 1.6 : ダスト層の膨張 フェイズ i) の初め短期間、ダスト形成が活発な時期、P = 0.6 で Δτ0.9 = 0 から P = 0.75 の Δτ0.9 = 7.75 まで急上昇する。その結果、 可視変光曲線は急落する。 フェイズ ii) 期のダスト層膨張により、光学的深さが減少して短波長 変光曲線は上昇する。 　長波長では P = 0.60 - 0.75 のダスト層成長が変光曲線中間極大を 引き起こす。それは新しいダスト層からのダスト熱輻射によるものである。 　タイムスケール　 　モデルＢ ではダスト形成、膨張のタイムスケールが脈動のタイムスケールに 比べて短かった。ところが、モデルＢ，Ｃ　では、それが逆となっている。 それは次に論じる。 　まとめると、　 （１）主に長波長で現れる中間ピークは、最内側ダスト層の光学的深さ の時間変化に強く依存する。 （２）フェイズ 0.35 - 0.70 に現れる短波長ピークは光球の輻射が見えた ものである。

図３a.ダスト形成開始期、t = 0.6*P での動径構造。

図３b.　t = 0.75*P での動径構造。

図４a.

図４b.

３．２．　 　モデルＡは周期的だが、Ｂ，Ｃには長期変動　 図５，６，７はモデル A, B, C の赤外変光曲線である。図５はモデル Ａが正確に周期的な変光を繰り返す事が示されている。ところが、モデル Ｂ，Ｃには準サイン関数的な変光にもっと長い周期の振動が重なっている。 この驚くべき振る舞いの説明には流体力学計算に戻る必要がある。 　多重周期度 (multiperiodicity) 　論文１では、新しいダスト層が各脈動毎に形成されるが、同時にダスト シェル全体の t = βP での構造は t = (β+nP)P と 等しい、つまり同じ構造が nP 回毎に繰り返されることを述べた。 nP は多重周期度 (multiperiodicity) と呼ばれ、この 詳しい解析はこの論文の範囲を超える。モデルＢでは nP = 4, モデルＣでは nP = 5 である。 　最内側ダスト層の成熟 fC = 1 に達する時間が脈動周期の何倍 かにより様々な多重周期度が現れる。 　モデルＢでの最内側ダスト層　 　長波長、例えば 25 μm、の変光曲線ほど全体の力学的振る舞いを 反映している。モデルＢでは新しいダスト層は深い極小期、 t = 2.5, 6.5, 10.5... P で形成される。この新しい層は外側に動いて行き、次の 層が出来る寸前、t = 6.0, 10.0, 14.0 ... P に成熟 fC = 1 に達する。 図６の極小 t = 2.5, 6.5, 10.5... P は単波長では異なる光学的深さを 有する。これは新しいダストが形成され始める半径が 0.5 Ro 程度変動する 為である。局所的熱力学的条件により、ダスト形成は t = 2.5, 6.5, 10.5... P より僅かに早く、従って少し内側で少し高温高密度の箇所で 開始される。これは新しい層の単波長光学的深さを大きくするので、 解析から深い箇所の物理条件の探索に向いている。詳しくは Fleischer et al 1994 を見よ。 ダスト層は t = 3.5, 4.5, 5.5 では形成されないのか？ 図６．様々な赤外波長でのモデルＢ変光曲線。縦軸スケールは波長毎に異なる。

図５．様々な赤外波長でのモデルＡ変光曲線。縦軸スケールは波長毎に異なる。 ( 2.2, 25 μm は図２と同じ？ そうは見えるけど。) 図７．様々な赤外波長でのモデルＣ変光曲線。縦軸スケールは波長毎に異なる。

　４．議論　

AFGL 1085 とモデルＡ　 　図８は AFGL 1085 の変光曲線。Le Bertre 1992 である。中間ピークが 見える。これはモデルＡの新しいダスト層形成によるものと思われる。 モデルＡの短波長( λ < 2.2 μm )変光曲線ではダスト層の 形成によりかなり狭い追加極大が生まれ、すぐに光学的深さの増加に 伴い低下して行く。この追加極大は光度増加による幅広の極大のすぐ 後に起こる。図２、５を見よ。 　長波長( λ > 2.2 μm ) 新しいダスト層の周期的形成は 上昇期の途中に低い中間ピークを作り出す。それはダスト熱輻射の寄与 である。しかし、観測される中間ピークの説明には、ショックエネルギー の大気内散逸(Feuchtinger et al 1993), 第２次ショック波の形成 （Bowen 1990, Willson et al 1994）などの説明も可能である。AFGL 1085, R Lep などの天体 (Le Bertre 1992) を　 0,90 - 100 μm で十分に 細かい時間間隔の観測が重要である。 また、画像上にダストシェルのさざ波、 段差が期待できる。 IRC +10216 にはそのような構造が観測されている ( Ridgway, Keady 1988) 図８． AFGL 1085 の変光曲線。Le Bertre 1992

R For とモデルＢ　 　R For の変光曲線はモデルＢとよく似た等級ドリフトを示す。Feast et al 1984 は R For が 1983 年に「異常に」深い極小を示したことを 報告している。似た深い極小は 1990 年にも Le Bertre 1992 によって 観測された。Alksnis 1990 は似たような数周期に及ぶ変動を他の幾つか の天体で報告している。 　我々のモデルではこの現象はタイムスケールの異なる幾つかの現象の 複合で生じる。一つは脈動のタイムスケールで起こる通常の変光で、 もう一つはダスト形成と成長のタイムスケールで、物理状況により 4 - 5 脈動周期のタイムスケールに成り得る。 図９．R For の変光曲線。三角＝Le Bertre 1992、バツ＝Feast 1984

　５．結論