Physical Conditions in the Circumstellar Envelope of α Orionis


Weymann
1962 ApJ 136, 844 - 865



　アブストラクト　

　α Ori 星周ラインの成長曲線を解析して星周層の物理条件を導いた。 原子コラム密度は 1022 個 cm-2 でマスロス率は 4 10-6 Mo/yr である。水素は多分中性で、メタルの第２電離は 重要ではないだろう。運動温度は 1000 K 程度である。 H, K 線を除いて、 中性と電離ラインの視線速度は同一である。 　ここ 20 年の間、星周ラインの速度または強度に系統的な変化は見られない。 星を囲む広範な彩層の証拠を議論する。 α Her の議論を簡単に行う。 星周層内の物質が高密度の塊りになるかどうかの吟味の結果、そのような集積 は考えにくいことが判った。

　１．イントロダクション　

　定常流出の発見　

　 Adams, MacCormack (1935) は M 型超巨星 α Ori の共鳴線が正常吸収線の視線速度よりブルーシフト していることを発見した。 Spitzer 1939 はそれを吹き上げられたガスを見て おり、電離が進んで落下状態は観測に掛からないというモデルで解釈した。 Deutsch 1956 は α1 Her の伴星 α2 Her に共通の星周吸収線を発見し、この星から定常的にガスが流出していること を確実にした。 		　赤色巨星期で燃やしきれない　

　一方、理論的な観点からは、質量星の進化は最終的には何らかの形で質量を 棄てざるを得ないことが判っている。そして、Salpeter 1958 は、Sandage 1954 を引用し、M 11 の赤色巨星枝の数では、先端までの時間では, 12 % の水素が燃えてターンオフした後、残りの水素を燃やしきれないという単純な 議論で、マスロスの必要性を証明した。


図１．TiI とAlI の星周線トレース。点線は仮想連続光。

　２．等値巾と成長曲線　

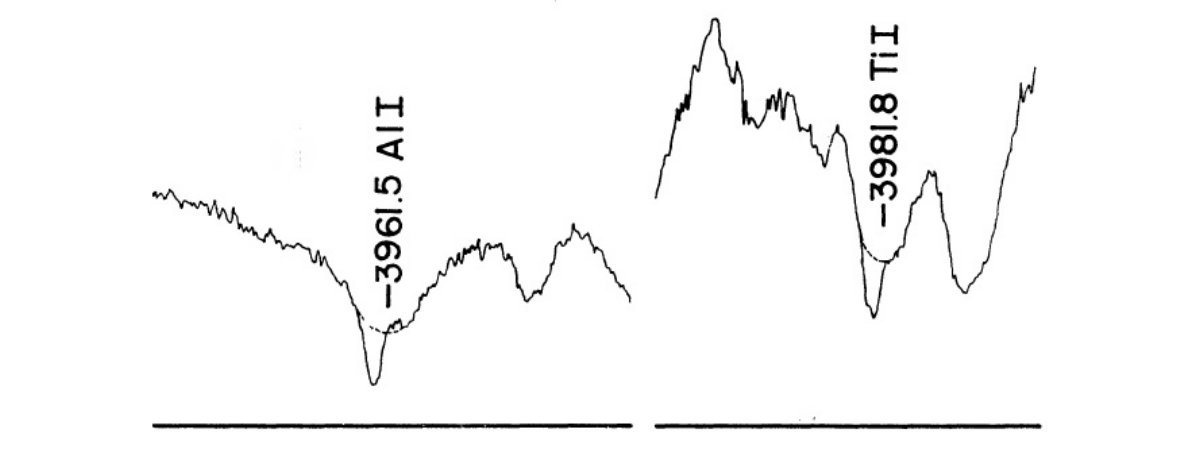
　光球吸収線と星周吸収線　

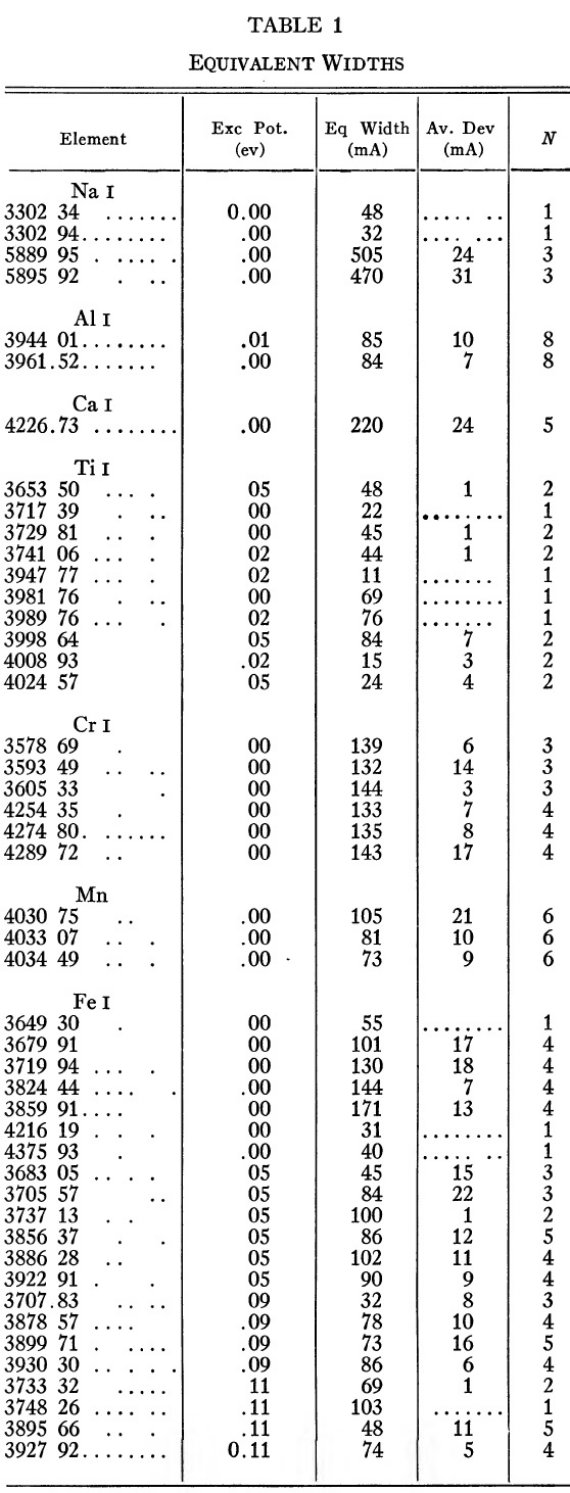
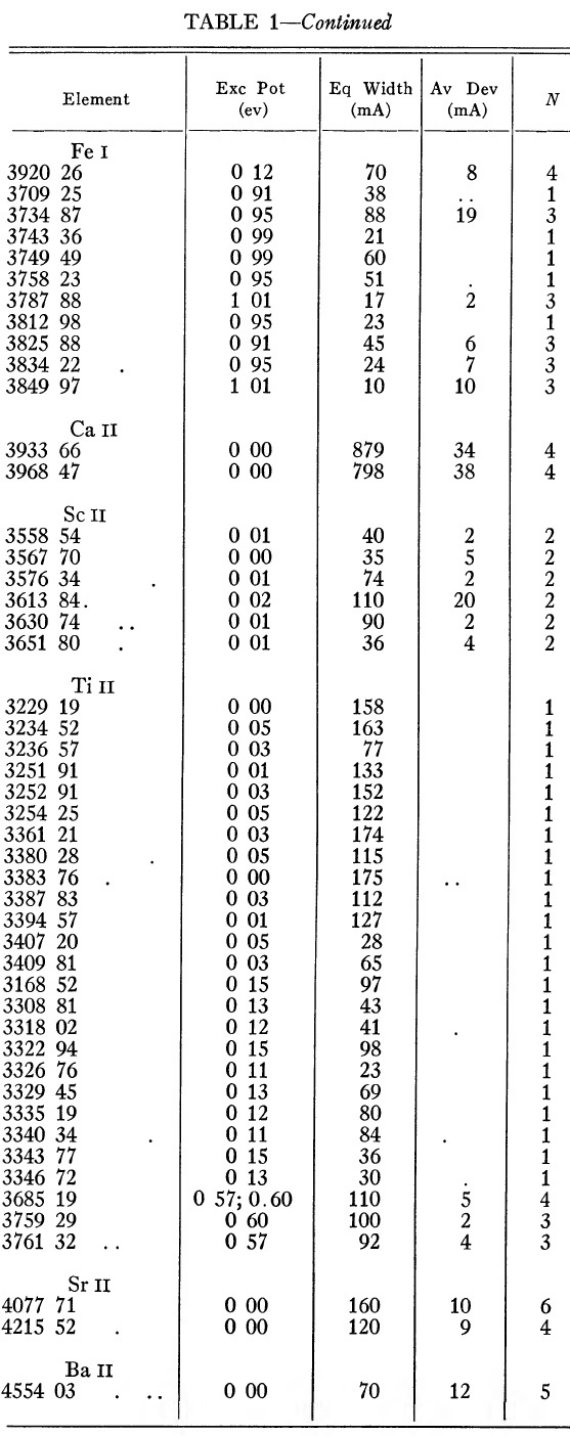
　マウントウィルソンで 1.9 A/mm の 3150 - 4900 A α Ori スペクトル が撮られた。図１にそのトレースの一部を示す。光球吸収線に星周吸収線が重 なっているのが分かる。光球線の中心は近くの正常な光球線の観測から決める。 近くにない場合はラインの赤側から中心位置を推定する。星間吸収線の等値巾 は図１に示したような有効連続光を仮定して計算する。 		　等値巾　

　表１に等値巾を示す。星周層の密度が低いので衝突励起は無視する。連続 オパシティは１よりずっと低い。理論成長曲線には純粋散乱の Schuster-Schwarzchild モデルを採用する。通常のモデルでは、光子は reversing layer に入り、数回 散乱によるランダムウォークの後にそこから脱出する。しかし、大部分は光球 に跳ね返され、吸収される。

　表１．α Ori 星周ラインの等値巾　

　
　

　広がった散乱シェル　

しかし、今回、星周層は大きく広がっているので、 跳ね戻された光子が破壊されるのは、小さな光球の作る立体角に入った時だけ である。したがって、視線方向に与えられた量の物質があるとき、シェル半径 が大きくなるほど、ラインは弱くなる。こうして、光学的に薄い、定常的で、 星に較べて十分大きな半径を有するシェルに対しては、シェルがあまりに巨大 で星から分解されることでもない限り、吸収核は見られない。

　膨張する散乱シェル　

　粗い定量解析に依れば、 x = r(shell)/r* としたとき、同じ吸収を生み出す のに必要な視線に沿った物質量は x2 に比例する。
(まったく分からない。コラム密度なら 同じはず。 )
シェルが膨張していると, Rottenberg 1952 が論じた通り、話しが全く変わる。 膨張速度を V、μ = 星と光のなす角度のコサイン、 とすると観測者に対し 光が 2Vμ レッドシフトするからである。　

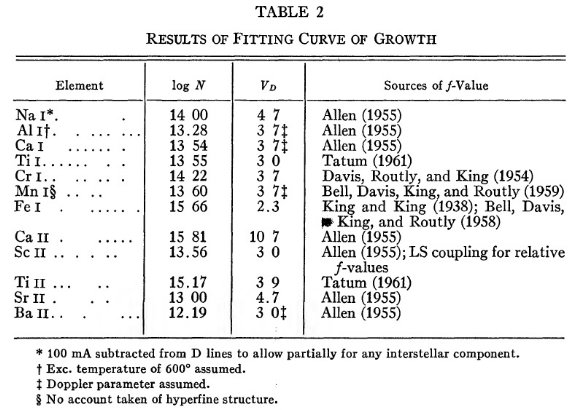表２．成長曲線フィットの結果




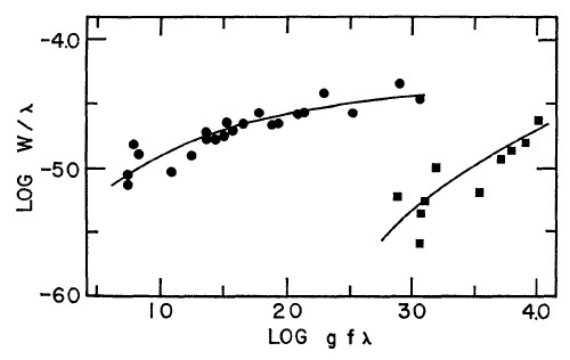図２．Fe I の成長曲線。黒丸＝a5D 項からのライン。四角＝ a5F 項からのライン。a5D 微細構造内の水平移動で 表５の励起温度へ移る操作が施された。


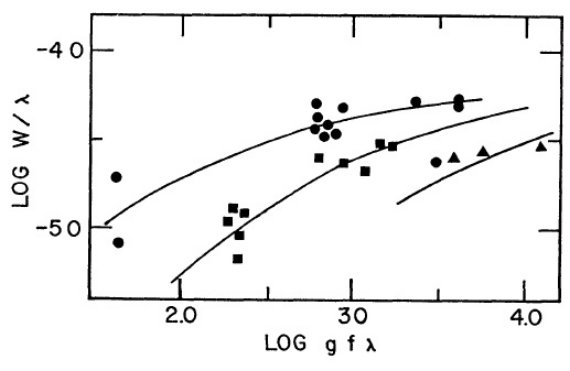図３．Ti I の成長曲線。黒丸＝a5F 項からのライン。 黒四角＝b5F 項からのライン。 三角＝a2F 項からのライン。

　３．α Ori シェルにおける電離と励起レベル　


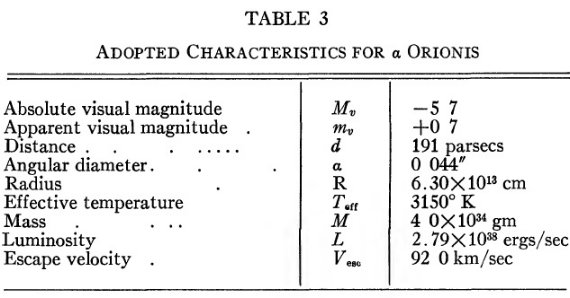表３．α Ori の物理特性

　　

　α Ori の物理特性を表３に示す。非常に低い励起レベルから、電離平衡 を星間空間と同じ方法(Stromgren 1948)で取り扱うことを可能にする。 C=基底状態以外のレベルからの再結合、高電離の補正定数、W=星の 光の希薄化ファクター、輻射場は Tc と W で特徴づけられる。Te=電子温度 とする。 そこでは電離平衡は次の式で与えられる。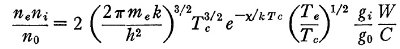

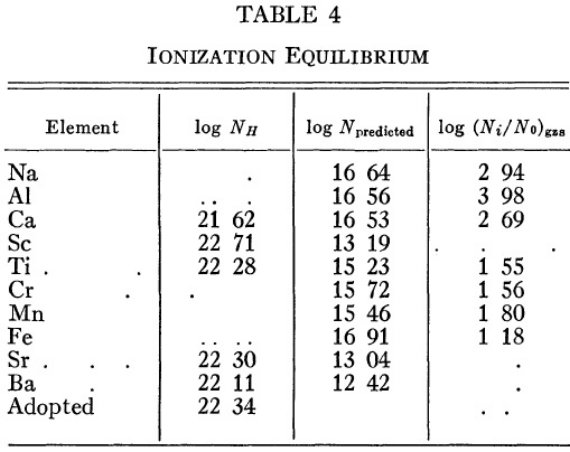表４．α Ori の物理特性

　表４＝電離平衡の結果　

　電離平衡式の結果を表４に示す。密度が r-2 で下がると同様に 輻射も下がる結果、電離度はほぼ一定に保たれる。


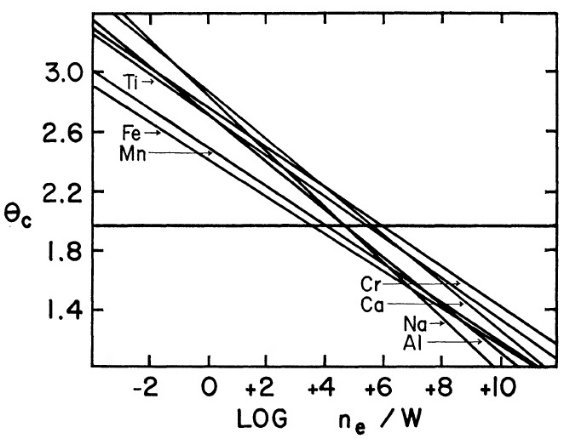図４．log(ne/W) と 夫々の元素に仮定するカラー温度 Tc の関係。 θC = 5040/Tc. θC = 1.96 を採用。 　



表５．励起温度

　４．マスロス率　

　　

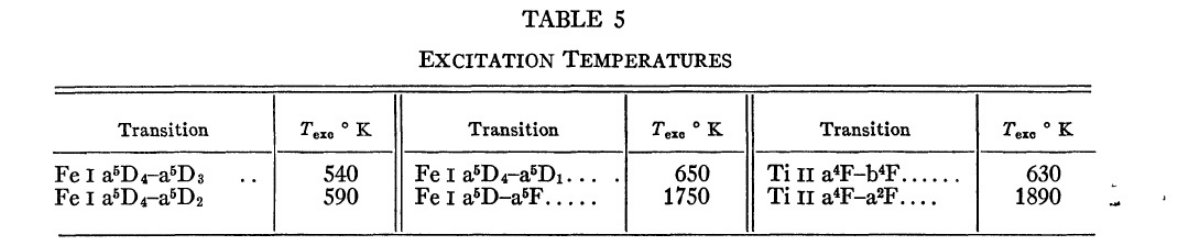
　r0 = シェル内側半径。 n0 = r0 に おける密度。N = コラム密度。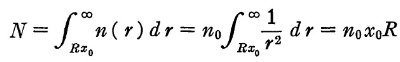





　　

　

　　

　 		　　

　

　　

　

　　

　



図．

　　

　　

　

　　

　

　　

　 		　　

　

　　

　

　　

　



図．

　　

　　

　

　　

　

　　

　 		　　

　

　　

　

　　

　



図．

　１．イントロダクション　

　　

　　

　

　　

　

　　

　 		　　

　

　　

　

　　

　



図．

　　

　　

　

　　

　

　　

　 		　　

　

　　

　

　　

　



図．

　　

　　

　

　　

　

　　

　 		　　

　

　　

　

　　

　



図．

　　

　　

　

　　

　

　　

　 		　　

　

　　

　

　　

　



図．

　　

　　

　

　　

　

　　

　 		　　

　

　　

　

　　

　



図．

　　

　　

　

　　

　

　　

　 		　　

　

　　

　

　　

　



図．

　　

　　

　

　　

　

　　

　 		　　

　

　　

　

　　

　



図．

　　

　　

　

　　

　

　　

　 		　　

　

　　

　

　　

　



図．

　　

　　

　

　　

　

　　

　 		　　

　

　　

　

　　

　



図．

　　

　　

　

　　

　

　　

　 		　　

　

　　

　

　　

　



図．

　　

　　

　

　　

　

　　

　 		　　

　

　　

　

　　

　



図．

　　

　　

　

　　

　

　　

　 		　　

　

　　

　

　　

　



図．

　　

　　

　

　　

　

　　

　 		　　

　

　　

　

　　

　



図．

　　

　　

　

　　

　

　　

　 		　　

　

　　

　

　　

　



図．

　　

　　

　

　　

　

　　

　 		　　

　

　　

　

　　

　



図．


( )


et al. () 先頭へ