Pulsation Phase-Drpendent Dust Shell Models for Oxygen-Rich AGB Stars

　アブストラクト　

　１．イントロダクション　

　２．ダスト外層モデルの計算 (Egan et al 1988)　

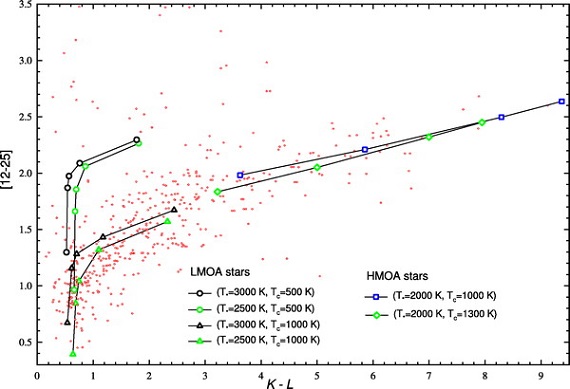
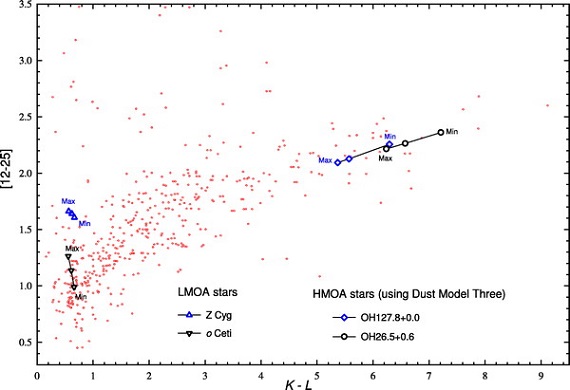
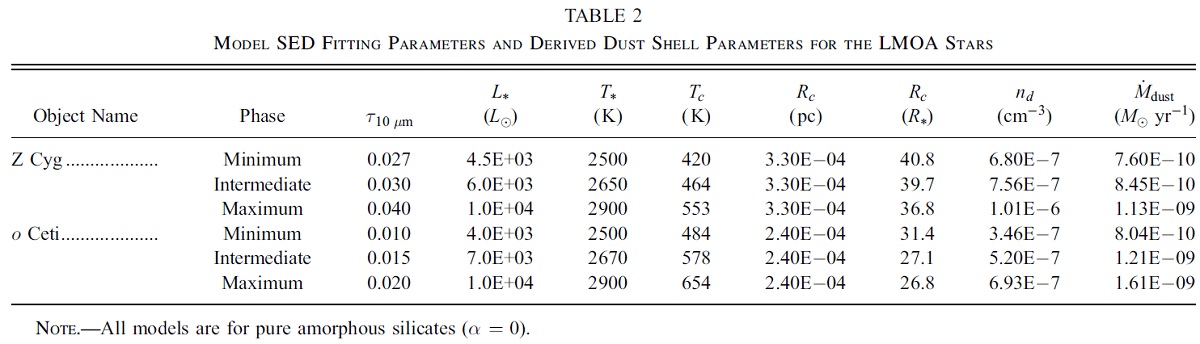
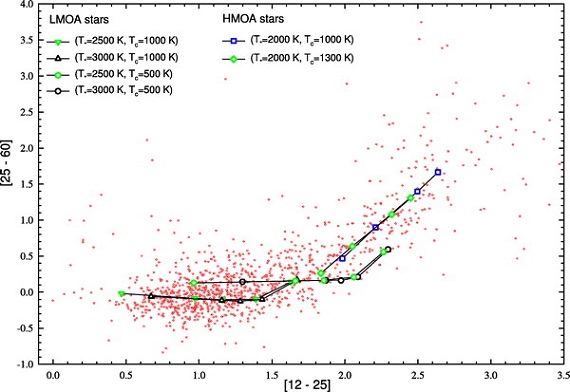
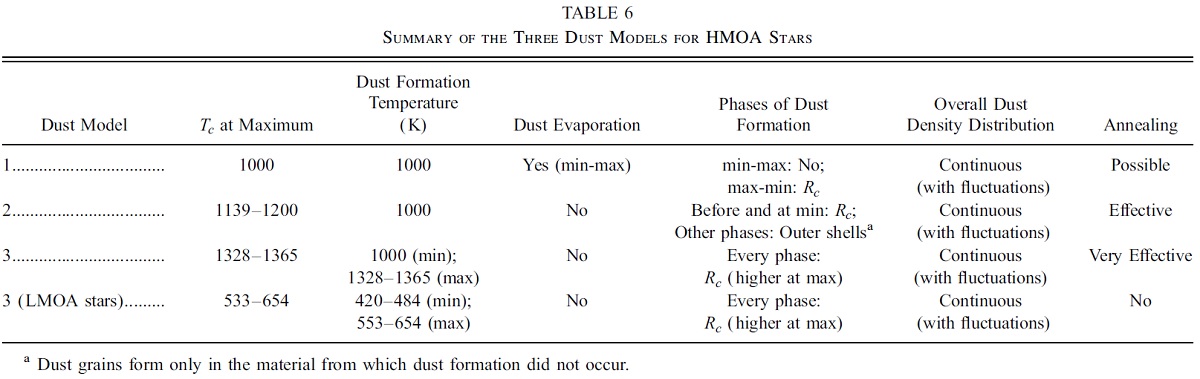
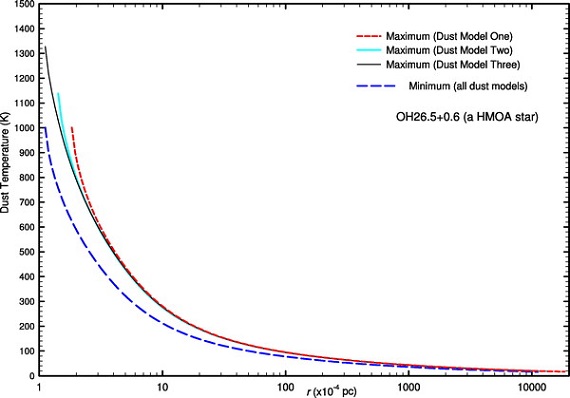
２．１．中心星　 　中心星として、 Ls = 4.0 103 Lo と 3.6 104 Lo を仮定する。Ls の変化は SED の形は変えないが SED 全体のレベルを変える。 中心星の Tbb は、特に LMOA では、SED に影響する。Ts = 2000 - 2900 K で変えて、影響を調べる。 (星のSED は黒体なのか？明言なし。) 　２．２．ダストシェルのパラメター　 密度分布 Rc = シェル内側半径、Ro = シェル外側半径として、Ro = 10,000 Rc 仮定。 ρ ∝ r-2 (r = [Rc, Ro])とする。 脈動に伴うマスロス変動 脈動に伴いマスロスレートはおそらく極大時をピークとする変動を繰り返すで あろう。しかし、Vexp = 10 - 30 km/s では密度揺らぎ帯の巾は Rc 以下なので SED の形に影響は小さい。 Tc の決定 SED の形は Tc に大きく影響される。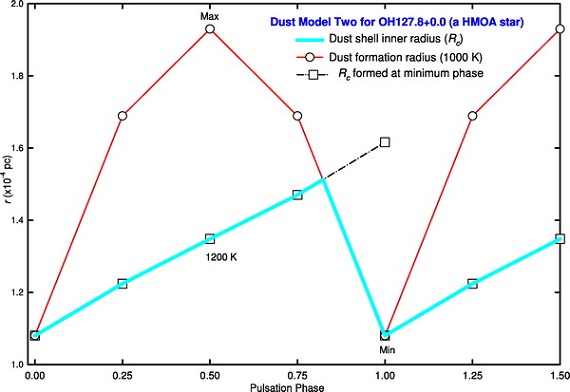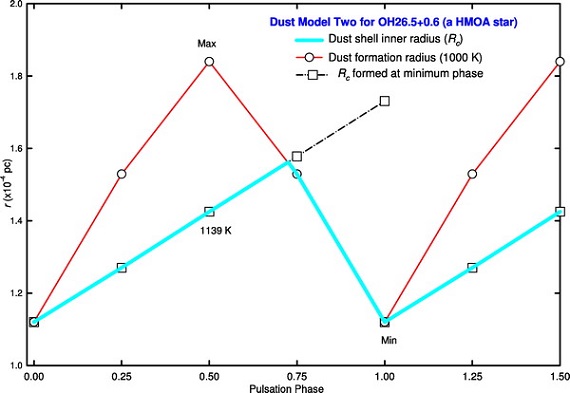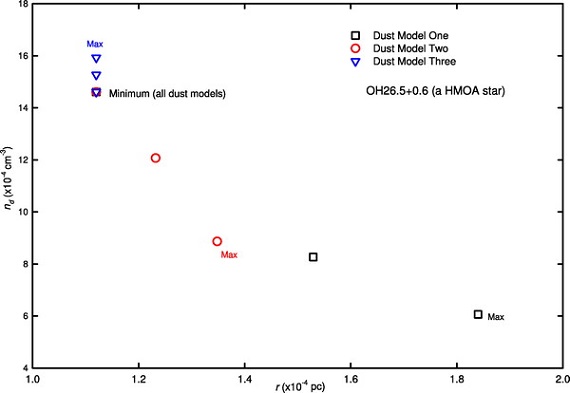 Rc の決定 Rc は SED にフィットする Tc によって決まる。したがって、 Tc も Rc も位相 の変化に対して一定値ではない。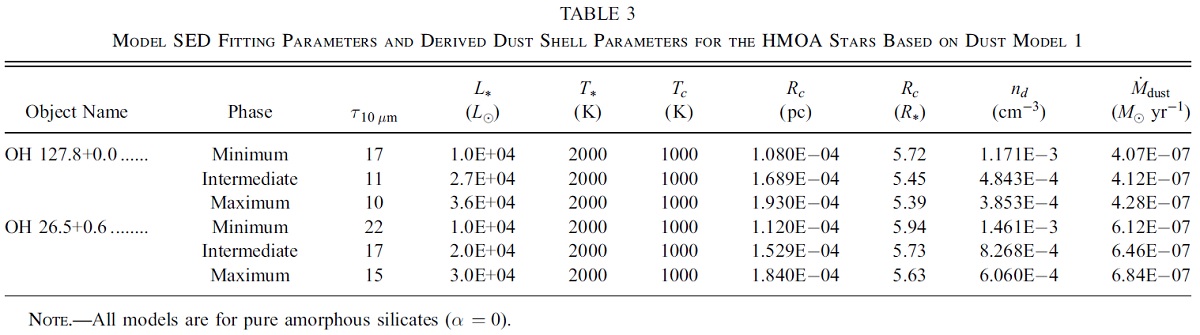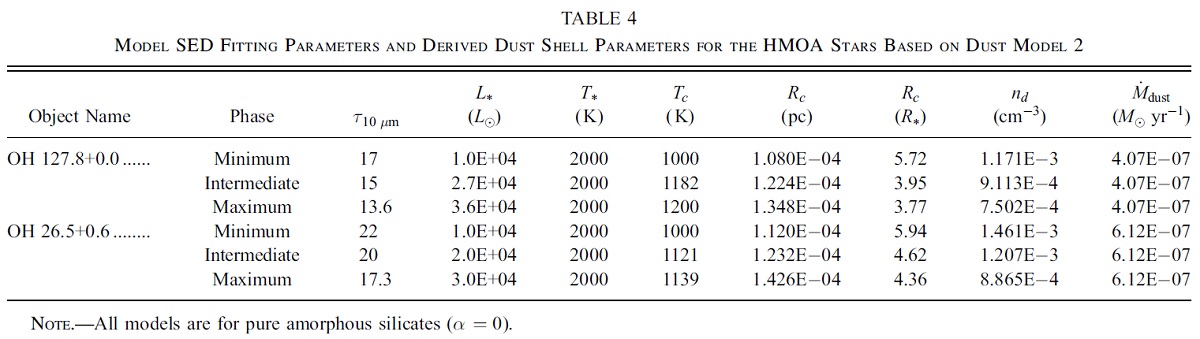 　２．３．ダストオパシティ　 　HMOA の FIR 放射に結晶シリケイトの特徴　 　非晶質(ダーティ)シリケイトは一般には O-リッチ AGB 星の SED に合う。 ＨＭＯＡ星の FIR スペクトルからは結晶シリケイトの放射が検出された。 LMOA からの結晶シリケイト放射は見つかっていない。 　α = シリケイトの結晶度　 　α = (結晶シリケイト重量)/(総シリケイト重量) Suh (2002) は HMOA の SED が α = 10 - 20 % でフィットすることを見出した。 　ダストオパシティ　 　ダストは全て半径 0.1 μm, ρ = 3.0 g cm-3 とする。 シリケイトオパシティは Suh (2002) から採る。 τ10 ≤ 3 の LMOA には暖かいシリケイトを、 τ10 > 3 の HMOA には冷たいシリケイトを使用する。 結晶シリケイトのオパシティには Jager et al 1998 を用いた。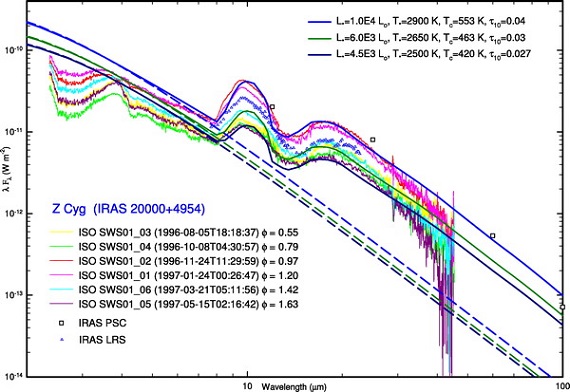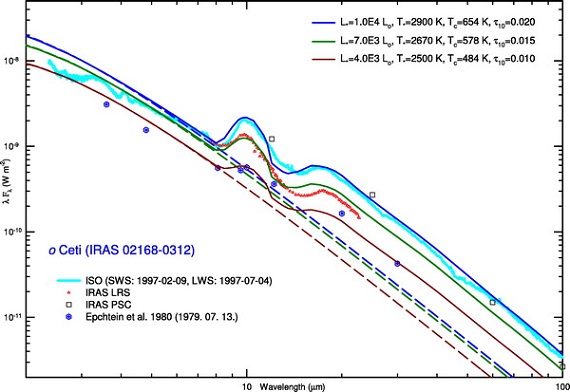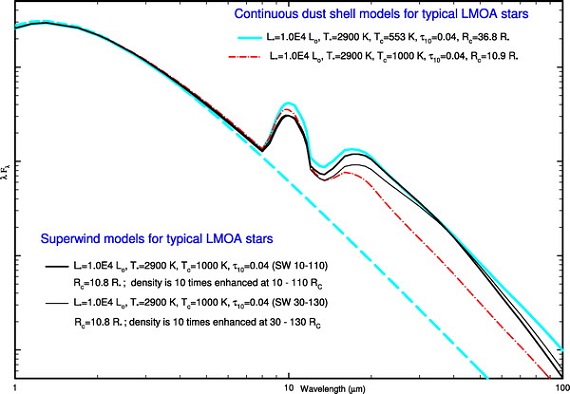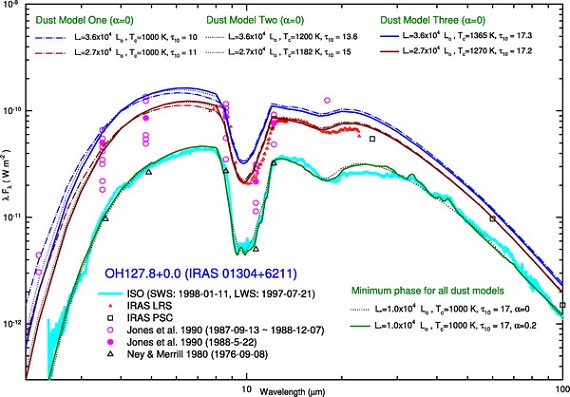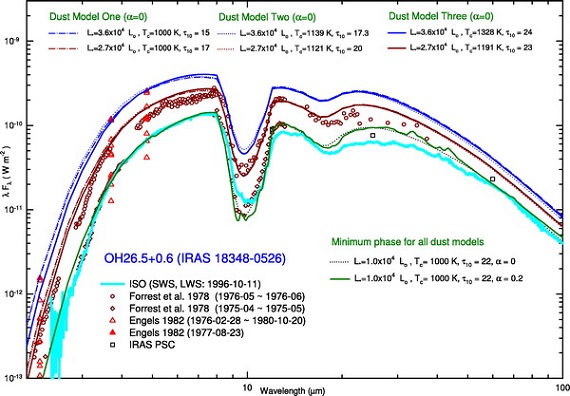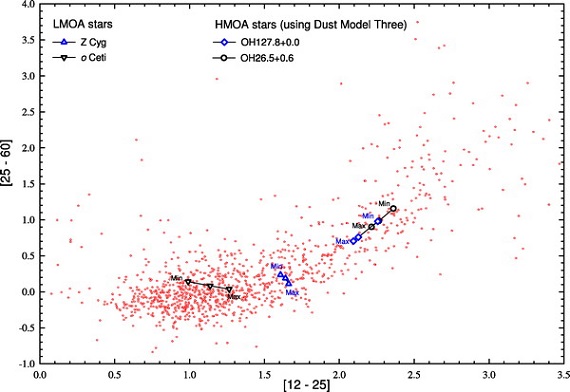 　２．４．基本モデルの結果　 　基本モデルの SED を図1に示す。破線＝中心星。上枠＝ LMOA. LMOA では中心星の温度 Tc が SED に強く影響する。下枠＝ HMOA.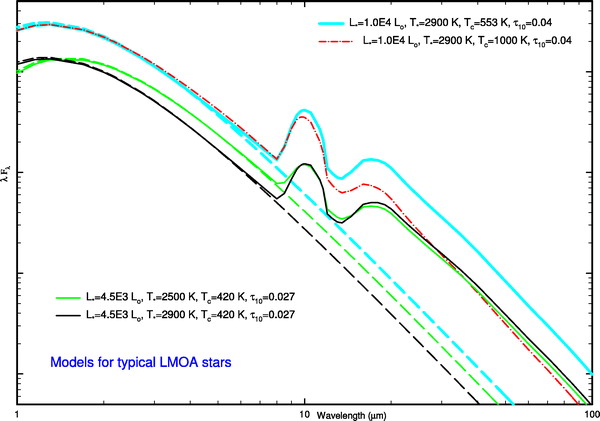

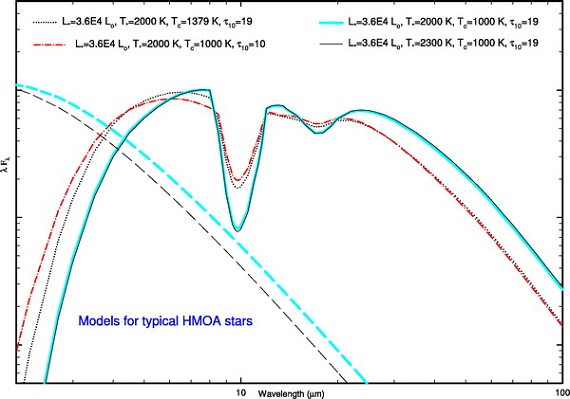
図１．典型的 LMOA と HMOA 星に対するモデル SEDs.破線＝中心星。 上枠：LMOA の SED は Ts と Tc に大きく影響される。 下枠：HMOA の SED は Tc に大きく影響される。非常に大きな τ10 の場合でさえ、高い Tc は浅い吸収帯を生み出す。Ts はあまり影響しない。

　３．観測 SEDs との比較　

図２．二つの LMOA 星の異なる位相での SEDs。ρ ∝ r-2. 　 　観測データは ISO SWS, LWS, IRAS PSC, IRAS LRS, 航空機から得た。 特に Z Cyg は Onaka, de Jong, Yamamura 2002 により６回の SWS 観測が なされた。この星は、シェルの特性が位相でどう変化するのかを研究する のによいデータを提供する。他の星では SWS は一回である。 　３．１．LMOA 　 　LMOA 星パラメター　 　LMOAs は位相に応じて Ts = 2500 - 2900 K とする。Tc は SEDs フィット から決める。

図３．LMOA 星の超星風モデルと安定星風モデルとの比較。 　 　図２＝Ls が増すと τ が大きくなる 　 　図２にモデルと観測の比較を示す。モデルとしては３つの位相に対応する 星パラメターを選んだ。極大時に Ts が高くなる。 Z Cyg, οCet の 双方で、Ls が増すと τ が大きくなることが分かる。 (位相によりマスロスに短期の変動 が起きると、τ に影響するのではないか？) 表２には LMOAs フィットパラメターを示す。 　マスロスレート　 　Vexp = 一定は文献値を用いた。ガス/ダスト = 100 を仮定して、マスロス レートを出す。 　マスロスレートは位相によって変化　 　Monnier et al 1998 は晩期型星の MIR スペクトル時間変化を観測した。 彼らは、10 μm 放射帯が極大期に鋭くなることを見出した。それには、 光学的深さの増加と新しいダスト形成を必要とする。実際、 表２にあるように、極大期には光学的深さとマスロスレートが最大になる。 その結果、密度分布には、変光周期に対応した波打ちが見られるはずである。 この検討は第４章で行う。 　ヘリウムフラッシュの効果　 　別の問題として、シェル全体の連続的密度分布の上に、密度超過帯が乗る 効果がある。Suh, Jones 1997 と Egan, Sloan 2001 はヘリウムシェルフラ ッシュに伴う超星風の効果を研究した。彼らはその結果として、密度超過帯が シェル内に出現するとしてその SED を計算した。それは超過帯がない場合と かなり異なることが分かった。図３には、この超星風モデルを図１，２の連続 風モデルと比べた。Tc = 1000 K, r = [10, 110] Rc で 10 倍の密度超過があ ると仮定して Z Cyg の ISO スペクトルと比べた。それは、より低い Tc の 連続星風モデルとよく似ることが分かった。 (その前に、変光曲線にヘリウムフラ ッシュを予想させる兆候が見られるのか？)

　３．２．ＨＭＯＡｓ　

図４．色々な位相の HMOA SEDs. 　明るくなると吸収が浅くなる理由は？　 　Ts = 2000 K を全位相で採用。極小期の光度 Lmin = 1 104 Lo. OH127.8+0.0 と OH26.5+0.6 を見ると、変光により中心星が明るくなると吸収帯 の深さは浅くなることが分かる。Suh et al 1990, Suh, Kim 2002 はこれを 光度が上がると、中心部のダストが蒸発するためと解釈した。しかし、ここでは 別の解釈を提案する。 　３．２．１．ダストモデル１　 　中央空洞の増減　 　ダストモデル１では 1000 K で凝結、蒸発する。従って、シェル内側温度 Tc = 1000 K に固定される。Suh, Kim 2002 はこのモデルで色々な位相にある二つ の HMOA 星を SED フィットした。極大期にかけて、シェル内側半径は増大する。 彼らは中心空洞の体積差の中にあるダストの約半分が蒸発すると見積もった。 (極小期までにできたシェルが外に 逃げていく。極大期に向かう期間ではそれを蒸発前線が追いかける。そして 半分が逃げ延びるということ？)

図５．モデル２パラメターの位相による変化。 　ダスト形成の周期的変化　 　仮にダスト形成が既に起きた領域ではダスト形成がないと仮定 すると、極小から極大の間にダスト形成は起きない。極大から極小の間は 内側半径が縮小するのでダスト形成が増加する。 図４には二つの HMOA 星の異なる位相での測光値と各位相でのモデル１フィ ットを示す。シェルパラメターは表３に示す。以上のような過程の結果、 シェルのダスト分布には周期的増減が乗るであろう。 (これは、前サイクルで作られたダストが、光度向上の 結果、蒸発する効果を極小から極大までダスト形成が起きない、極大から極小の間に作られた ダストが飛んでいくというモデルなのか？図５でも枠外では出来たダストが 次のサイクルで増大する Rc に追い越されるのか？ どうも不明確。) 　蒸発温度　 　もしダストグレインが 1000 K より高温で蒸発しないなら、全過程が異なる。 ダストグレインの破壊はより過酷な環境が要求されるだろうから、ダストモデ ル１は物理的には不適当である。中心星からの輻射はダストの破壊には不十分 であるので、Tc は容易に 1000 K を超えるであろう。

　４．ダストシェルモデルの議論　

マスロスレート　 　SED 比較から、LMOA 星では 10-8 - 10-7 Mo/yr, HMOAs で (4-7)×10-5 Mo/yr と評価される。これは 過去に観測から決まった値の範囲に合う。 　ダスト形成温度　 　過去の研究ではダスト形成温度を一定値 1000 - 1500 K に固定していた。 ダスト形成過程の研究から、強い星風ではダスト形成温度が上がる（Kozasa et al 1984）ことが予想される。Sogawa, Kozasa 1999 によると、ダストは 温度は密度、圧力に依り異なる温度で凝結し、一度形成されると、ダストグ レインは輻射冷却で急速に 900 K (4 10-5 Mo/yr) から 500 K (5 10-6 Mo/yr) へと下がる。 (出来たとたんに周囲のガス温度と 解離して下がるのか？しかし冷えたダストがガスを冷やすのでは？ しかし、シェルモデルではガス温度分布はダスト温度で決めているのではない か？だからダストの平衡温度が低い所では、最初からガス温度は低く与えて あるのでは？つまり、高温でダストが形成され、その後急速に冷却という過程は ダストモデル自体に含まれないと思うのだが。そこがどうもピンと来ない。) 　Tc について　 　ダスト蒸発温度はよく分からない。スパッタリングやグレイン衝突のような 過程がダスト破壊に必要であろう。極大期でも輻射による加熱は蒸発には不十分 である。したがって、シェル内側温度は容易にダスト形成温度を上回る。 　再結晶化　 　Fabian et al 2000, Hallenbeck et al 2000 は非晶質シリケイトの熱進化 を調べた。彼らは 1000 K でアニールすると短時間、スモークで１日以下、で 非晶シリケイトを結晶シリケイトへと変わることを見出した。LMOAs ではダスト 形成温度が 1000 K なのでアニーリングが進まない。これが LMOA では結晶 シリケイトが見つからない理由である。もし HMAO で Tc ≥ 1000 K になる と非晶質シリケイトの再結晶化が進む。 　LMOA とダスト蒸発　 　LMOA ではシェル内側温度 Tc はダスト形成温度に等しい。極大期でも蒸発の 証拠はない。したがって、極大期には星風が強まり、ダスト形成と光学深さは 極大期に最大となる。極大時に Tc = 654 K である。ダスト形成温度は 極小期に 400 K, 極大期には 600 K であることが分かった。ダストモデル３ が LMOA に適当である。 　LMOA の Rc 　 　LMOA で見出された Tc = 420 - 654 K は Rc = 27 - 41 Rs に対応する。 低マスロスレートと大きなシェル内側半径は低密度を意味する。その密度 ではニュークリエイションやダスト成長には低すぎる。Sogawa, Kozasa 1999 は Rc < 10 Rs としたので我々のモデルとは合わない。 　他の解釈　 　３．１．節に述べたが、LMOA に超星風の密度超過を加えると、ダスト形成 温度を上げて Tc = 1000 K, Rc = 10.9 Rs で連続密度分布モデルのと似た SED を得る。こうなるとアニーリングも可能となる。Kemper et al 2001 は 非晶質と結晶質シリケイトが混ざっている場合、モデル SED は必ずしも 結晶の特徴を示さないと述べた。さらに高精度で多くの観測がこの問題に 解決を与えるであろう。 　図６上 = HMOA OH25.5+0.6 のシェルパラメター　 　図６は HMOA OH25.5+0.6 のシェルパラメターが位相にどう依存するかを示す。 上枠はシェル内壁位置とダスト密度、下枠は温度分布を示す。 温度分布のパターンがダストモデルにより変化することが分かる。 ( log - log 表示にしろよ)

図６．３つのダストモデルに対し、異なる位相における 上枠＝シェル内壁ダスト密度と、下枠＝温度分布の比較。 　 もしモデル1を採用すると、極大前にシェル内側の高温領域ではダストが蒸発 する。ダストモデル２を仮定すると、極小期及びその後に作られたダストグレ インは極大にかけて 1000 - 1139 K にまで高温化する。ダストモデル３では 極小期に 1000 K で作られたグレインは極大期まで 1000 K 以上で存在し、 極大期に 1328 K で作られたダストは中間位相より後では 1000 K 以下となる。 　アニーリング　 　アニーリングの効率で見ると、モデル３が最高、モデル１が最低である。 どのモデルでも HMOA の環境はアニーリングが可能である。 　図６下 = HMOA OH127.8+0.0 のシェルパラメター　 　HMOA OH127.8+0.0 のプロットは HMOA OH25.5+0.6 と似ている。 LMOAs のモデル３プロットもよく似ている。 　表６ =シェルパラメター　 　表６ にシェルパラメターの特性をまとめた。HMOA に対しては３つの異なる ダストモデルは同じくらい良く合う。我々はダスト蒸発温度は形成温度よりずっと 高いと信じるので、モデル２か３を押したい。両者の間では３の方が好ましい。 こちらの方だけが連続的なダスト形成を実現し、極大期に大きなマスロスを 実現するからである。もしもダスト形成温度がシェル内側ダスト温度ほど早く 上昇しない場合には、より現実的なモデルとしてはモデル１と２の中間が考え られる。

　５．赤外二色図　

図７．LMOAs と HMOAs の IRAS 二色図 　 　図７、８の上枠＝異なる光学的深さ　 　図７には 1316 O-リッチ AGB 星の λFλ 二色図 (Suh et al 2001) を、図８には 504 O-リッチ AGB 星に対して、K-L 対 [12-25] 二色図を示す。図中の大きなシンボルはモデル計算の結果である。 上枠の LMOA モデルは τ10 = 0.01, 0.05, 0.1, 0.5, 3 を 異なる Ts と Tc の組み合わせに対して示した。HMOA に対しては τ10 = 7, 15, 30, 40 モデルを異なる Tc に対して示す。 　図７、８の下枠＝異なる位相　 　下枠には二色図上の位置が位相でどう動くかを示している。HMOA に対しては モデル３のみを示す。

図８．LMOAs と HMOAs の [12]-[25] 対 K-L 二色図。 　 　カラー変化の逆転　 　図７の下枠を見ると、 LMOA では [12-25] が極大で赤く、 HMOA では 逆に極小で赤いことが分かる。これはつまり、 LMOA では F25 の振幅が F12 より大きいことを意味する。しかしながら、Z Cyg の ISO SWS データを積分して得る結果は逆の関係を示唆する。Z Cyg の [12-25] は、 極小で 1.36, 中期で 1.29, 極大で 1.21 である。我々のオパシティは 10 μm 帯を上手く再現できず、 [12-25] は吸収帯に強く影響される。 それがモデルが観測を再現しない」原因かも知れない。LMOA では 観測とモデルの予測は一致する。 つまり LMOA に対しては、は位相によるカラー変化を 説明するモデルではない？しかし放射帯強度は良さそうだった。放射強度と 連続光カラーの関係が少しおかしいのでないか？このあたり、じっくり観測で 攻めるべきかも。

　６．結論