| 厚いダスト層を持つ OH/IR 星 OH 127.8+0.0, OH26.5+0.6,のスペクトル エネルギー分布 SED を様々な変光位相で調べた。ISO データを用い、新しい 脈動パラメタ―を定めた。深いシリケイト吸収帯は脈動位相に応じて大きな 変動を示した。この変動は主に OH/IR 星ダスト層の性質の変化に起因する。 詳細な輻射モデルを観測と比較して中心星と周辺ダスト層のパラメタ―変動を 変光位相によりどう変化するかを追った。 | その結果、中心星が極小から極大へと光度上昇する際に、シェル内側半径が 大きくなり、その変化速度はガス膨張速度より大きいことが判った。ダスト 層の光学的深さは減少する。光度が極小から極大へ向かう際には、ダスト形成 は停止し、体積差(?)の中のダストの半分が蒸発しただろう。 極大から極小への期間には内側半径が縮小するので、ダスト形成が盛んに起き ているの違いない。ダスト外側半径では一定のダスト風が容易に維持されてい る。変光により引き起こされるダスト蒸発が OH/IR 星内側ダスト層における ダストの再結晶化機構である可能性がある。 |
|
OH/IR 星とは OH/IR 星は一般に、赤色巨星枝を離れる寸前の酸素過多 AGB 星と看做され ている。この時期にあるミラ型星は長い周期の大きな変光と高い質量放出率 (10-7 - 10-4Mo/yr)に伴うダストに富んだ星風で特徴 づけられる。OH/IR 星は脈動しているが、ダスト層の外側速度は 10 - 30 km/s の一定値を示す。これは変光周期よりずっと長い時間スケールでは質量 放出率が一定であることを意味する。 低質量放出率の星モデル Forrest et al 1978, Le Bertre 1988 が示したように、変光位相に伴い、 光度だけでなく SED の形も変化する。SED の変化から重要な情報が引き出せ るはずである。Le Bertre 1988 は炭素星ミラ R For を変光位相の関数として モデル化した。さらに、Le Sidaner, Le Bertre 1993 は二つの酸素過多ミラ を位相の関数としてモデル化した。Monnier et al 1998 は AGB 星の中間赤外 スペクトル時間変化を調べた。Lobel et al 2000 は薄いダスト層を持つ酸素 過多ミラのモデルを立てた。これ等の研究は全て質量放出率が低い酸素過多 AGB 星が対象であった。従って 10, 18 μm バンドは放射帯である。 |
OH/IR 星の研究 Suh et al 1990 は 10, 18 μm に吸収帯を持つ OH26.5+0.6 を脈動衝撃波 モデルの結果を用いて研究した。Jones et al 1990 の測光研究は多数の OH/IR 星の変光を明らかにした。今や、ISO を初めとする新しい観測データを用い、 厚いダスト層を持つ OH/IR 星の研究が可能となった。 厚いダスト層の時間変化 本論文では、二つの OH/IR 星、OH 127.8+0.0, OH 26.5+0.6 の SED 時間 変化を調べる。我々はダスト層と中心星のパラメタ―を変光位相の関数として 求める。OH/IR 星の周りのダスト層はダストグレインの形成と破壊過程の 良い実験室である。 |

|
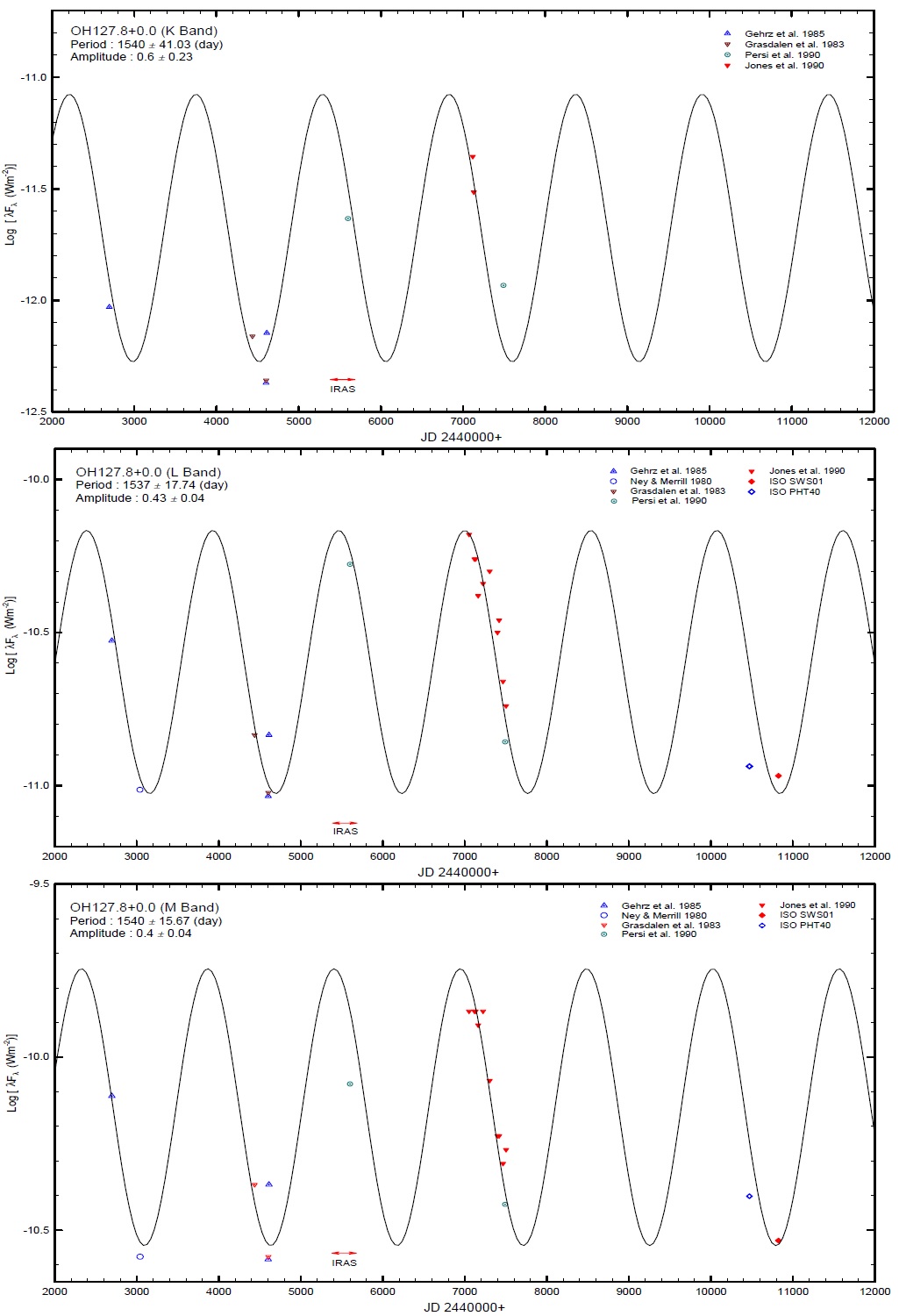
測光データ 二つの星の測光データは Gezari et al 2000 の Fifth Catalog of Infrared Observations と新しい ISO データを用いた。表1に用いたデータを示す。 データが全体傾向からかけ離れた場合は棄てた。表1には採用した数と棄てた 数の夫々を載せた。データの時間変化はサインカーブでフィットした。 |
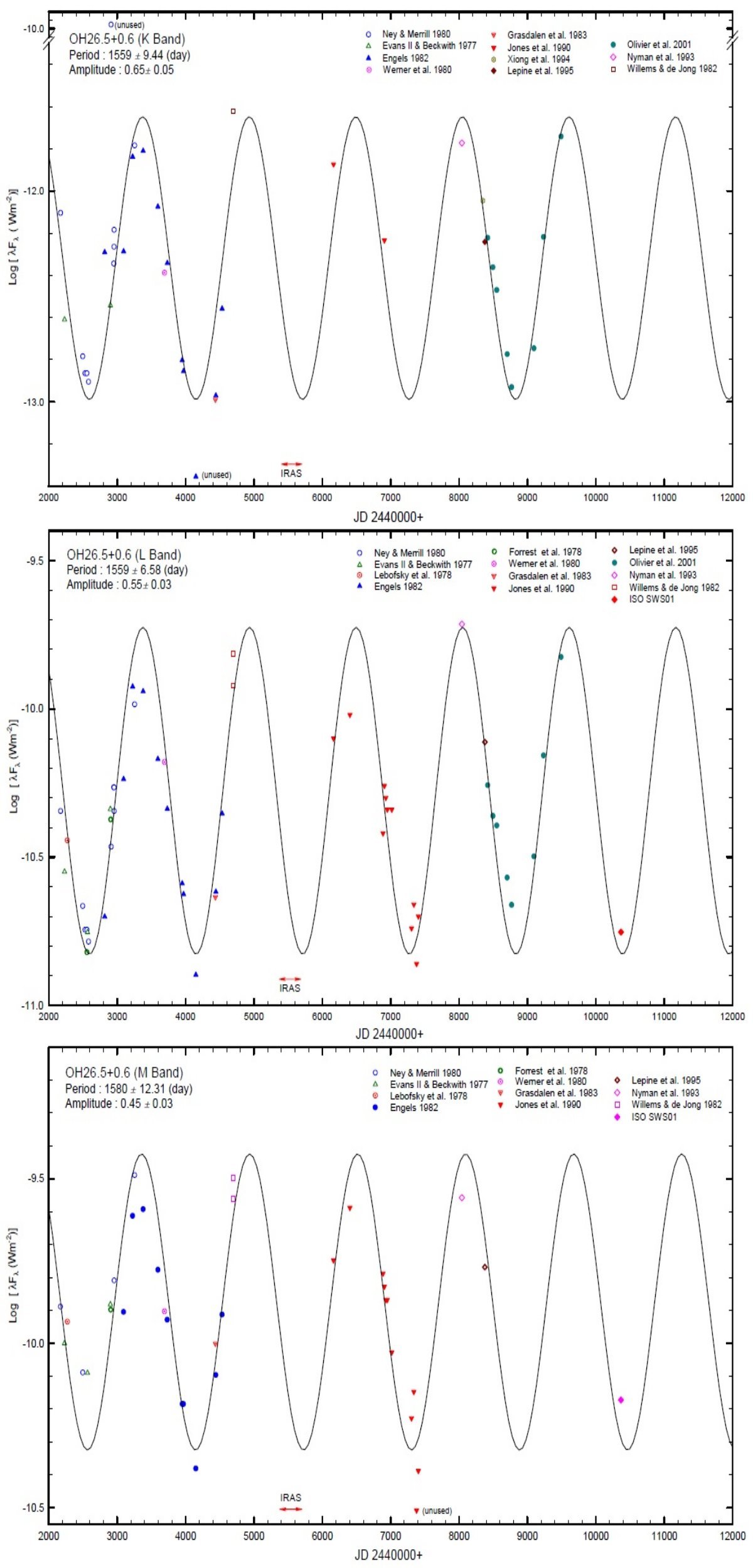
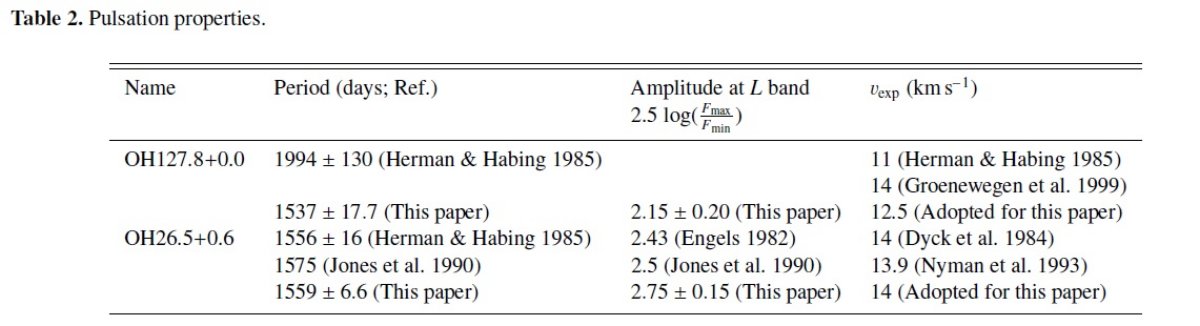
変光曲線 図1、2は二つの星の 25 年に及ぶ変光曲線である。図2には変光曲線に 使用しなかった3点も示した。ISOデータは極小期に撮られていることが 分かる。Lバンド変光曲線は最も信用できるので、変光パラメタ―はそこから 得た。表2には今回得られた変光パラメタ―と以前の結果を較べた。 |
モデル計算コードは Egan et al 1988 を使用した。ダストオパシティは
シリケイトに固定した。変数として τ10 を採り、 0.01 -
36000 μm の SED を計算した。
3.1.中心星極小光度を L = 104Lo とした。この値自体は全体のSED 強度 を決めるだけで、重要ではない。星のスペクトルは 2000 K 黒体と仮定する。 星の表面温度は変光位相により変化するが、その影響はマイナーで無視して も良い。光学的に薄いダスト層では中心星温度変化は確かにスペクトルに 影響する。しかし、光学的厚いモデルでは中心星温度を 1800 K から 2200 K まで変えても SED には僅かな変化しかない。 |
3.2.ダストシェル凝結温度 Tc と凝結半径 Rcダスト凝結温度を Tc = 1000 K と仮定する。ダスト凝結半径 Rc から ダストシェル外側半径 Ro = 10,000 Rc とする。詳細は Suh 1999 を見よ。 また、ダストの密度分布を ρ ∝ r-2 と仮定する。 ダストオパシティ Suh 1999 は AGB 星に最もよく合うダストオパシティを二つ定めた。一つは 10 μm 放射帯に合う暖かいダストオパシティ、もう一つは吸収帯を持つ 星に合う冷たいダストオパシティである。冷たい非晶質シリケイトのオパシティ には Suh 1999 のものを、結晶シリケイトのオパシティとして Jager et al 1998 を採用した。フォーステライトとエンスタタイトの比率は等しいと仮定 する。 ダスト粒子 結晶度 α = (結晶シリケイト質量/総シリケイト質量) とし、 α = 0, 0.1, 0.2, 0.4 のモデルを計算した。ダストの平均オパシティ は二種の単純荷重平均とし、ダスト粒子は半径 0.1 μm, ダスト鉱物 の密度は 3 g cm-3 とする。 |
|
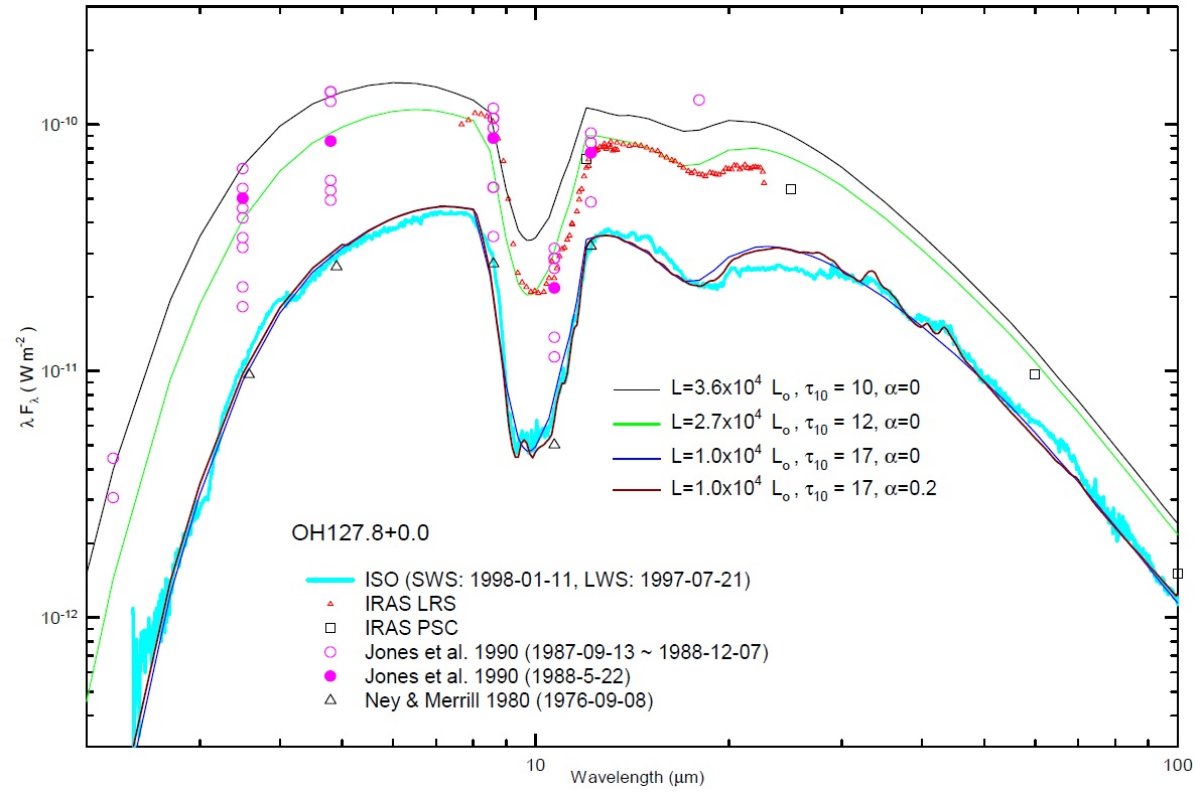
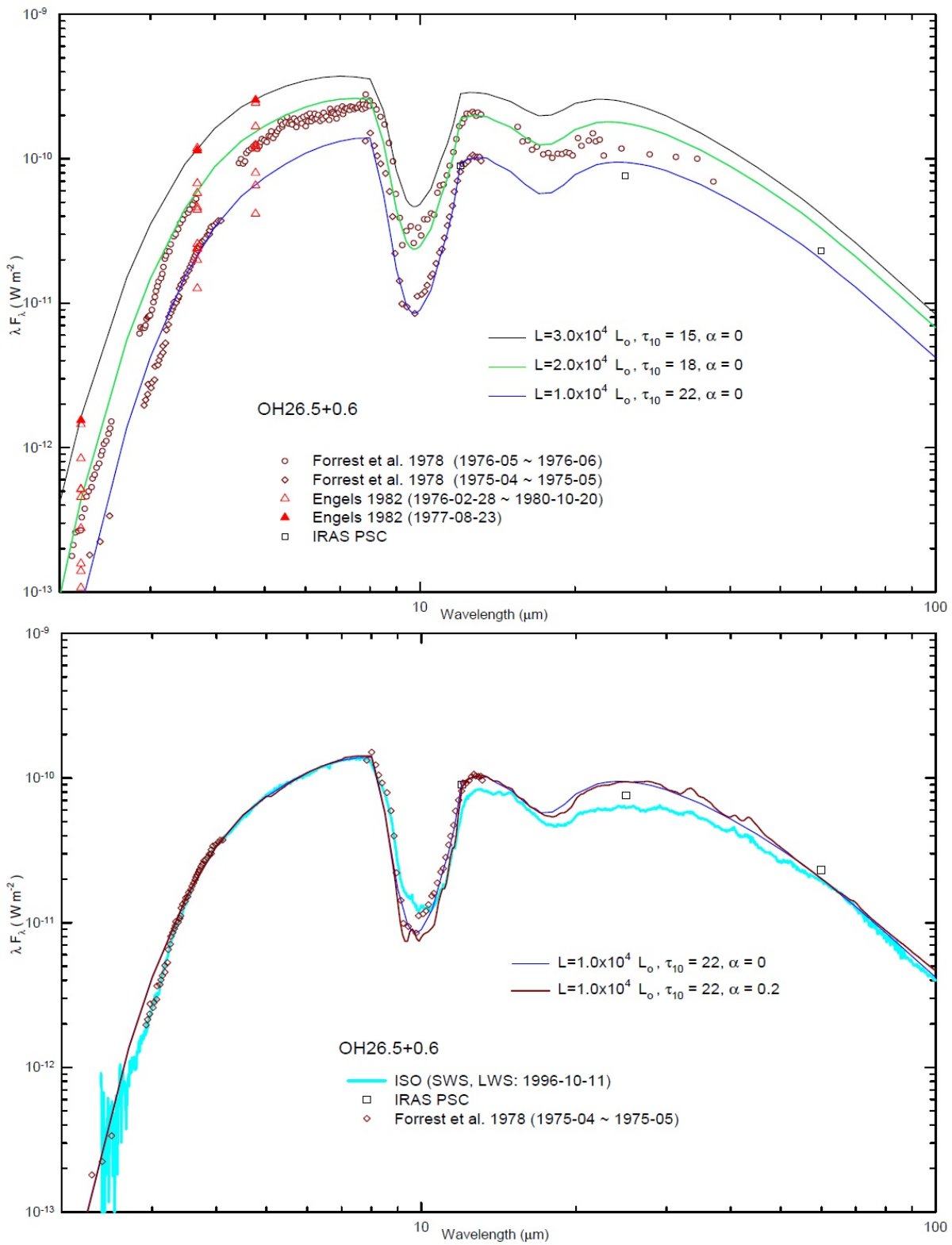
観測データ モデルとの比較には IRAS PSC, IRAS LRS, その他の地上観測データを用いた。 ISO SWS と ISO LWS に関しては、有意な多位相スペクトルを得られなかった。 そこで、最良の精度を持つデータを Sylvester et al 1999 から採った。 OH 127.8+0.0 図3に SED の比較を示す。図3には OH 127.8+0.0 を較べた。この星は 大きな輻射等級の変動を示す。極小位相のフィットは良い。中間、極大位相で は観測にあまり良く合わない。特に 8 - 9 μm でそうである。20 % 混合比 モデルは 19.5, 23.1, 27.3, 33.3, 40.6, 43.3 μm に強い結晶性構造を 示す。ISO 極小期スペクトルには 33.3, 40.6, 43.3 μm に明らかな放射帯 が見える。この放射帯を再現するには α = 0.2 が必要なのである。 OH 26.5+0.6 図4には OH 26.5+0.6 との比較を示す。上図は3つの位相での比較である。 極小、中間期のモデルは Forrest et al 1978 の観測に良く合っている。 下図は ISO データを 極小期モデルと較べた。ここでも極小期の ISO スペク トルには明らかな結晶性バンドが 33.3, 40.6, 43.3 μm に見える。 ここでもモデルフィットには α = 0.2 が必要である。 |
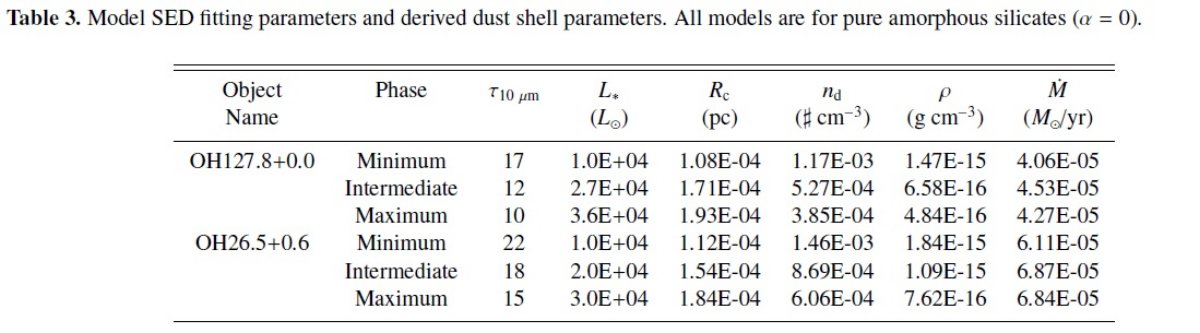
光度が上がるとダストが蒸発 どちらの天体も中心星光度が上がると、ダスト光学的深さが浅くなる。 我々は、ダストシェル内側において、光度が上がると大量のダスト蒸発が起きる と考える。表3には SED フィットパラメタ―の位相による変化を示す。 質量放出率 v = 一定を仮定すると、質量放出率は次の式で与えられる。 dM/dt = 4πr2ρv = 4πRc2 &rhoc;v ここに、&rhoc は Rc における密度(ガス)で、次の式で与えられる。 &rhoc = (4πa3/3)ρb ndβ ここに、 β = (ガス+ダスト)/ダスト の比である。β = 100, ρb = 3 g cm-3 を仮定すると、観測質量 放出率に合う値が得られた。 |
|
ダストモデル 表3から中心星が明るくなるとダスト層内半径が大きくなることは明らかである。 図5には位相と内半径の関係を表3からプロットした。全体としては r-2 上に乗っている。ダスト層の輻射輸送モデルは、Jones, Merrill 1976, Rowan-Robinson, Harris 1983, Bedijn 1987, Volk, Kwok 1988, Suh 1999 が調べた。これらは全て、球対称 r-α 密度分布 を仮定している。特に α = 2 が多く用いられた。 Rc の変化は SED に大きく影響する ダスト形成点付近 Rc の密度分布は単純なべき乗則より複雑である。(Suh et al 1990)しかし、3 - 5 Rc より外側では膨張速度が一定となり、変光期間 を通して密度は定常である。Rc 付近の密度分布を変えても天体 SED にはあまり 影響がない。(Suh et al 1990) ただし、 Rc を少し変えるだけで SED は大きく 変化する。 ダスト形成は 1 週間程度 単純な輻射圧モデル (Kwok 1975, Kozasa et al 1984) も、脈動と衝撃波を 組み込んだモデル (Bowen 1988, Suh et al 1990) も 全体として r-2 密度分布を予想する。モデルはダストへの加速はかなり急で 3 - 5 Rc の間に 定常速度に到達する。ダストの形成期間も 1 週間程度で非常に短い。 |
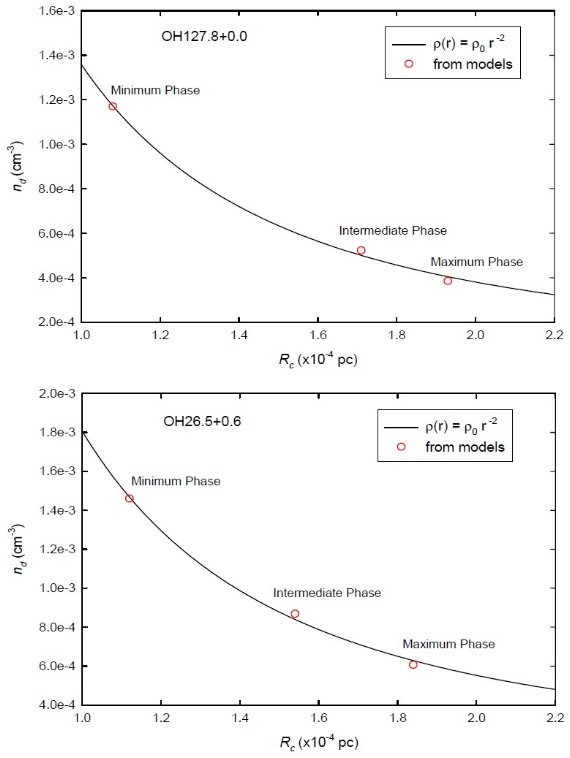 図5.ダスト凝結温度となる半径でのダスト数密度と変光位相の関係。 |
|
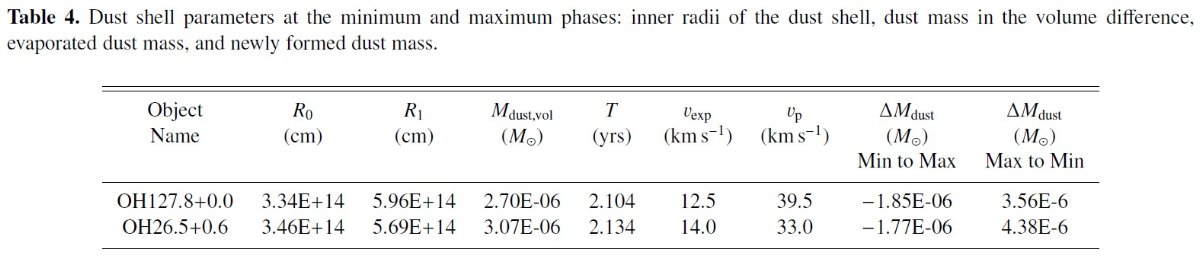
蒸発モデル どちらの OH/IR 星も極小から極大まで 2.1 年かかる。中心星の光度は 3 倍 になり、ダストシェルの内半径は増大するはずである。もし、内半径の増加速度 が星風速度を上回るなら、大量のダストが蒸発するだろう。ダスト蒸発を次の 簡単な仮定でモデル化する。 (1)(dM/dt) と vexp は一定。 (2)密度分布 ρ ∝ r-2 は不変。 すると、極小時と極大時のダスト量の差は、 ΔMd = 4π∫r-2ρd dt ≈ 4πRo2ρod∫0 T(vexp - vp)dt ここに、Ro = 極小時の内半径, ρod = Ro でのダスト質量密度 である。 |
vp = 内半径の移動速度は次式で与えられる。 vp = (R1 - R0)/T ここに、T = 極小から極大までの時間、R1 = 極大時内半径である。 表4にこれらのパラメタ―を示す。 ( R(L(t)) から vp(t) が出るのだが。) 半分が蒸発 表4を見ると、内半径移動速度は星風速度を上回ることが判る。従って光学 的深さは減少する。極小から極大に掛けて、ダスト形成は停止し、ダストシェ ルの体積差内のダストの約半分が蒸発するに違いない。表4を見よ。 (なぜ全部でなく半分なのか? ああそうか、星風で動く分ね。でもこの評価を頑張る意味はないな。) どちらの星でも3年の間に 2 10-6 Mo のダストが破壊される。我々の r-2 分布は粗すぎるかも知れないが、ダストシェルパラメタ―の 変化を捉えるには十分である。 |
|
極大から極小に掛けてのダスト形成 極大から極小に掛けて星の光度は 1/3 以下になり、内半径も減少する。極大期 から極小期の間に付け加わるダスト質量は、 ΔMd = 4πRo2ρod∫0 T(vexp + vp)dt これは極小から極大へ向かうときの式と同じだが vp の符号が反対 である。表4の最終列にはこの ΔMd を載せた。極大から極小 に向かう間ダスト形成は強化される。なぜなら内半径が縮小するからである。 表5には、変光の異なる位相間隔におけるダスト形成率を示した。 |
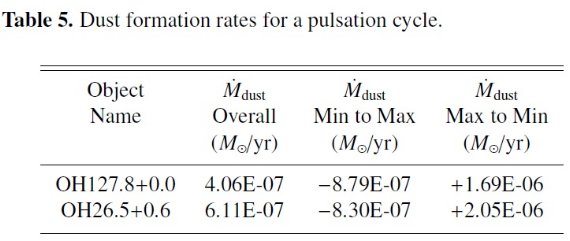 表5.変光期間内のダスト形成率 |
|
アニーリング Suh 2002 は、非晶質シリケイトして形成されたダストの一部は内半径付近で アニーリングにより結晶化すると論じた。もしダスト形成温度が 1000 K なら、数百日の間内径付近の温度は 900 - 1000 K であろう。 質量放出率が低いとアニーリングが起きない 小笹ら 1984, Gail, Sedlmayr 1999, Sogawa, Kozasa 1999 はダスト層が厚い 場合、ダスト形成温度はそれ以上に高くなりことを示唆した。もし、質量放出率 が低い星で、ダスト形成温度が 1000 K よりずっと低い場合にはアニーリングは 起こりにくいだろう。これが、低質量放出星で結晶シリケイトが発見されない 理由ではないか? |
蒸発時に結晶化 ここで展開した議論に基づき、我々は脈動で駆動されるダスト蒸発が OH/IR 星内半径付近でのダスト結晶化機構であると考える。非晶質ダストとして生ま れたダストが部分的に蒸発する。それら部分的蒸発ダストは結晶質かも知れない。 結晶質グレインは、光度が極小から極大へ向かう際により効率的に作られる だろう。なぜなら、蒸発はその時期にしか起こらないからである。 |
|
1.周期と振幅 ISO を含む新しい赤外データを用いて、新しい周期と振幅を決めた。 2.内半径移動速度 変光の極小から極大にかけて、ダスト内半径の移動速度は膨張速度を上回る。 ダストシェルの光学的深さは低下する。 3.ダストの蒸発 極小から極大に掛けてはダスト形成が停止し、差分体積内のダストの約半分 が蒸発する。 |
4.ダスト形成の強化 極大から極小に掛けては内半径が縮小する結果、ダスト形成が強化される。 5、結晶化 ダスト蒸発が結晶化機構である。 |