Variability of Supergiants in M 31 from the Palomar Transient Factory

　アブストラクト　

　１．イントロダクション　

　２．M31 の RSGs　

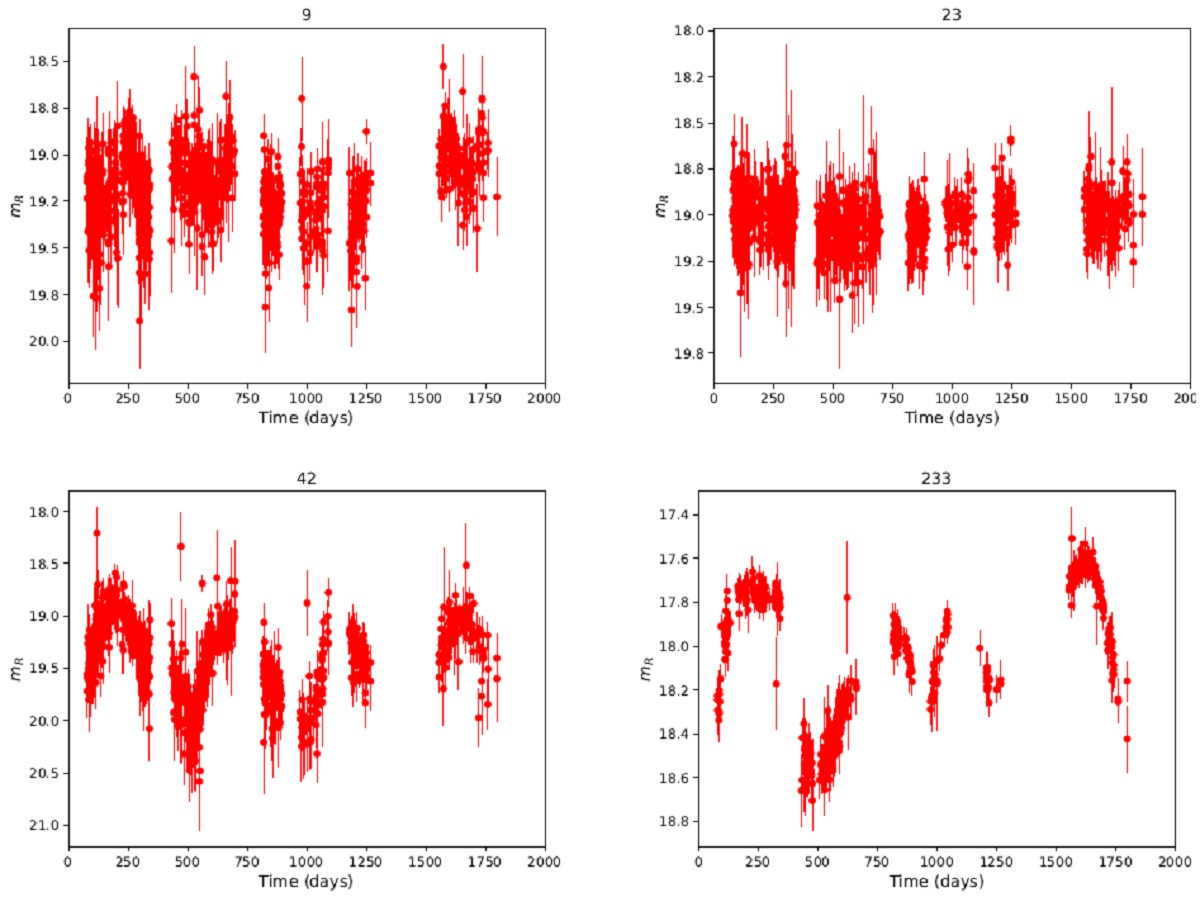
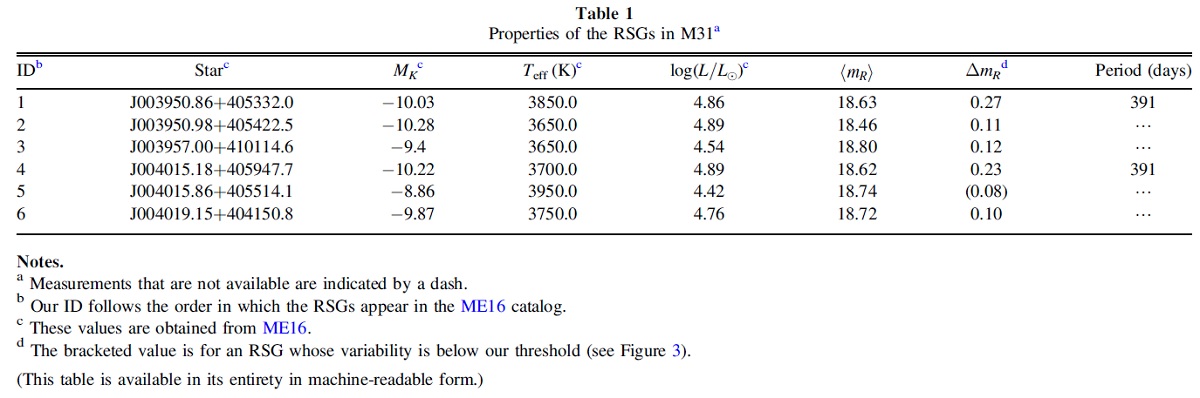
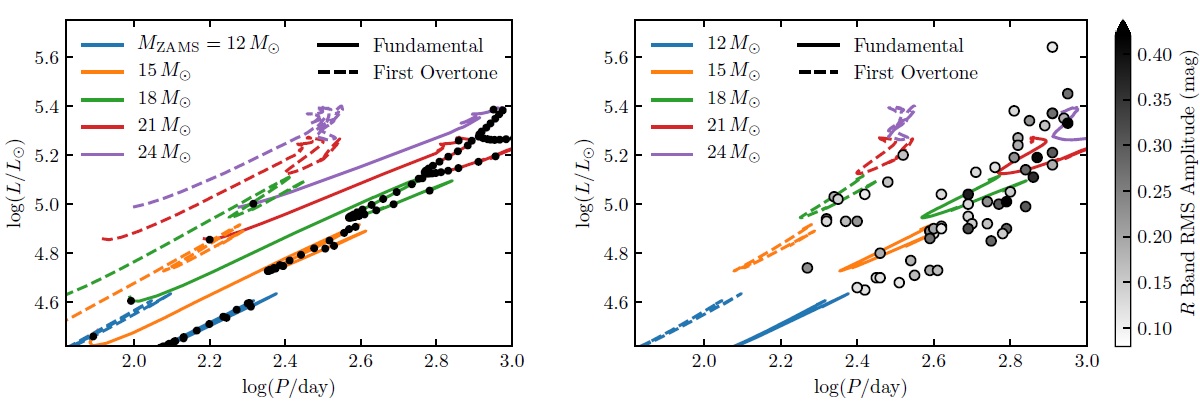
２．１．RSG サンプルとその物理的性質　 　RSGs の分別　 　Local Group Galaxies Survey (LGGS) は KPNO と CTIO 4-m 望遠鏡で行わ れた。M31 の UBVRI 画像から、350,000 星のカタログが公開された。 限界等級は 21 mag である。 Massey (1998) は測光法で RSGs を分別する方式を完成させた。それにより前景矮星は除去さ れる。我々はその中の (B-V)-(V-R) 二色図を採用した。Massey et al 2009 は RSGs 候補として 437 天体を選んだ。 Massey, Evans 2016 はその中の 255 星 の分光観測を行い、視線速度を測った。こうしてメンバーシップを確定した。 彼らは MARCS モデルを観測スペクトルにフィットして有効温度を決め、さらに BCK(Teff) を得た。こうして、既知の K mag と Massey, Evans 2016 はサンプル星の光度、有効温度を決めた。最後に、 GENEVA 進化経路と比べて、Mi を求めた。スペクトル型は Levesque et al 2005 に従い、 TiO と G-バンド、CaI 4226 強度で決めた。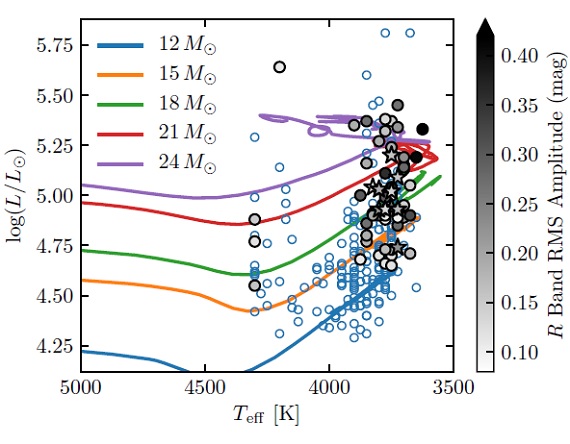 　有効温度問題　 　Davies et al 2013 は、 TiO バンドが形成されるのは大気上方なので TiO フィットから決める Teff は 数百 K 低い値を出すのではないかと述べた。 彼らはSED フィットから、彼らが解析したマゼラン雲の RSGs 全てに対し Teff = 4150±150 K を得た。しかし、Massey et al 2017 は、この Teff の 一様性はメタル量により RSGs スペクトル型が変わるという観測事実、また ハヤシ限界が低メタルほど高温側に移るという理論モデルに合わないと反論し た。 (反論になっているのか？ ＳＥＤから温度を 決めるのは不当か？) このように、 RSGs の温度スケールの問題は未解決である。この論文では、 Massey, Evans 2016 の K-等級を専ら用い、その光度をモデル進化経路との比 較に用いる。 (有効温度を回避？) 　２．２．iPTF データ　 　iPTF サーベイ　 　iPTF サーベイはその前任である PTF 観測と同じ、1.2 m パロマーシュミッ ト望遠鏡に 11 枚 CCD を付け、7 deg2 モザイク画像を撮った。 像の FWHM = 2" である。観測は 2012 年 5 月から 2017 年 2 月までほぼ連日 行われた。やく80 % は R, 20 % は g バンドが使用された。

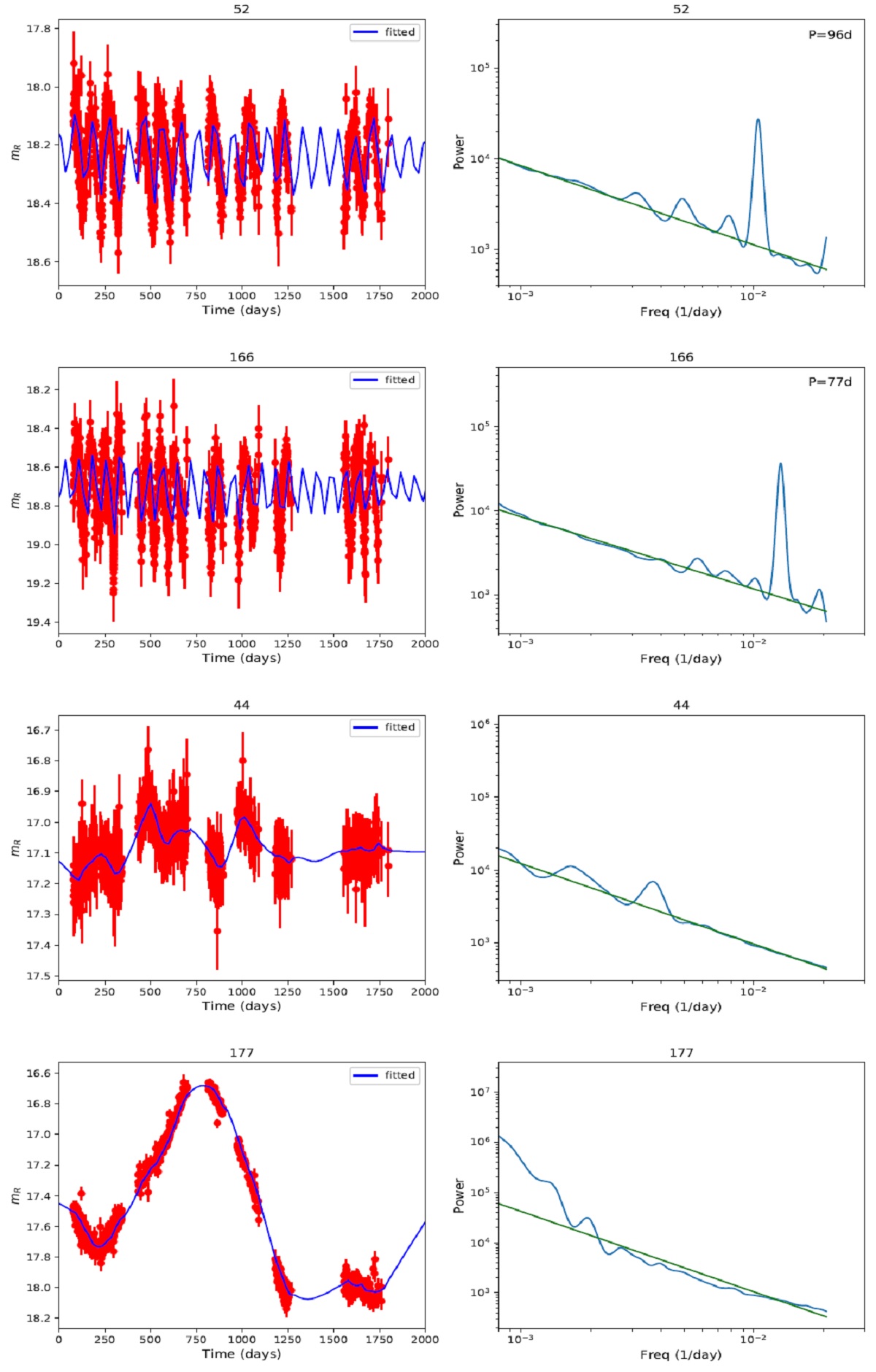
図１．M31 の iPTF R-バンド画像。 　差分画像　 　ここでは、 R-画像約 10,000 枚の解析を行う。このデータセットは 1500 晩 の観測から成り、 6 CCD による 1.8 x 2.4 deg2 を写している。 差分画像から変光天体を見つける方法を採用した。こうして検出された天体の カタログを「生変光カタログ」と呼ぶ。

　２．３．可視変光曲線　

forced photometry　 　「生変光カタログ」には、PTF 領域内にある RSGs 全て 253 星が載っ ていた。 (ME16 の分光サンプル 253/255 ？) しかしこの生カタログは差分操作で生じた人工的な変光、例えば位置合わせ 誤差による双極性パターンや明るい星をマスクした際の漏れ出しなど、を多数 含む。その解決に変光基準値を上げるとサンプルの完全性が損なわれるので、 差分画像に "forced photometry" を施し、RSG 光度曲線を作って、その変光 を個々に調べることにした。差分測光は混んだ領域で発生する問題を軽減する。 差分に伴い人工的に生じた測光値は光度曲線上で暴れ点として現れるので、容 易に処理できる。 　アパーチャ測光　 　Soraisam et al. 2017 と同じやり方で RSG 位置でのアパーチャ測光を行っ た。アパーチャ半径変化に対するフラックスの成長曲線を作り、個々の星に 大してフラックス補正を行った。次に、天体から差し引かれたフラックスが、 参照画像の PSF 測光で決めて、加えられる。測光精度の悪い９星を落とした。 図２に光度曲線の例を示す。 　rms 等級偏差　 　PTFIDE 変光検出パイプラインに掛からなかった星を "static star" と呼ぶ。 図３には "static stars" の rms 等級分散度と R 等級の関係をプロットした。 赤い丸は RSGs である。⟨mR⟩ = 18 - 19 ではいくつか の RSGs の R 等級変動は "static stars" と同程度である。そこで、眼視に よって、変動幅がノイズ程度の RSGs を有意に変更している RSGs から分離す る境界線を図３に引いた。167/253 = 70 % の RSGs に変光が確認された。 　変光と光度の関係　 　図４には rms 分散度と平均 K 等級及び光度との関係をプロットした。データ は ME16 から採った。低光度では変光のあるなしが重なっているが、「変光な し」 RSGs がある光度以下に偏在することは明らかである。MK < -10, log(L/Lo) > 4.8, では全て「変光アリ」となる。またその多くは、 ΔmR > 0.1 である。

図３．青十字＝"static stars" の rms 分散度。赤丸＝ RSGs. 橙実線＝眼視で引いた変光星境界。境界より上の RSGs の周期を求めた。 実赤丸＝有意な周期が求まった RSGs. 　進化モデルとの比較　 　我々のグラフは log(L/Lo) > 4.6 で変光が始まることを示唆する。 Yoon, Cantiello 2010 のモデルでは log(L/Lo) = 4.95 が下限である。 ただし、彼らは計算内で強いダンピングを掛けているので、彼らは脈動に 対して "lower limit" を置いたのみである。 (？) 我々の結果はしかし、彼らが見出した脈動の下限 16 - 17 Mo より低質量 の星が脈動可能であることを示している。また、振幅と光度の間の相関がある かも知れないことを示唆している。

　２．４．周期決定　

　３．M31 RSGs の PL Relation　

図６．M31 RSGs の MK-P 関係。青線＝フィット。ただし、左側の 平行系列を成す 12 星を除いた。点のカラーは右側に示す PTF 光度曲線 rms 振幅を示す。 　二つの P-MK 系列　 　図６には周期 P が得られた 63 RSGs の K 等級 (Massey, Evans 2016)をプ ロットした。51/63 個は (logP, MK) = (2.4, -9.5) - (3.0, -11.5) で揃った系列を成す。しかし 10/12/63 個が log P で 0.3 ずれた別の系列を 成している。 　短周期変光星は超長周期セファイド？　 　残りの 2/12/63 個(ID = 52, 166) は P < 100 d である。Kiss et al 2006 は P = 100 - 150 d の短周期 RSGs を報告している。しかしこれほど 短い周期の例はなかった。図５に示すように、ID 52, 166 双方とも極めて 規則的な変光を示す。その温度は Massey, Evans 2016 スケールで 4300 K と 高く、光度 MK ≥ -9.5 は低い。これらの物理的特徴は Fiorentino et al 2012 が述べた超長周期セファイドと重なる。実際、RSG 166 は Riess et al 2012 ではセファイドに分類されている。Massey, Evans 2016 の RSG サンプルは T < 4300 K の M31 星を選んでいるので、セファイド 不安定性帯の冷たい側の縁が RSG とされる可能性もある。 　周期等級関係とエラー　 　12/63 RSGs を除き、線形フィットをすると次の式が得られる。 　　　MK = (-3.38±0.27)xlogP + (-1.32±0.75) この RSG 関係式は M31 では初めてである。この関係式の周りの偏差は 0.29 mag である。この散らばりの一部は 2MASS の等級誤差(約 0.1 mag) であり、 単期測光であるための振幅効果, 0.18 mag 程度、から来る。星周減光もある 程度は聞くかもしれない。

図７．様々な銀河に対して、P-MK 関係の、青＝勾配と赤＝切片の 比較。 　さらに長周期の星？　 　明るい星ほど変光性が高くなり、 rms 散布度も大きくなる。また周期と光度 の相関を考慮すると、周期が検出されなかった明るい天体の中には今回扱った 周期範囲を超える長い周期の変光星が潜んでいる可能性がある。 　　 　図７には今回の P-MK 関係を他の銀河でのそれと比較した。 我々の勾配と切片は Kiss et al 2006 が銀河系 13 RSGs から得た値とその 偏差 0.46 mag に整合する。その上、それらは Yang, Jiang 2012 が LMC (47), SMC (21), M33 (40) で得た値とも合う。それらの散布度は 0.3 mag である。 　RSG PLR の普遍性　 　これらから、メタル量の異なるいくつかの銀河で得られた RSG PLR には普遍 性があるようだ。これは、RSG 脈動が水素の κ メカニズムで駆動される という現在の考えとも合う結果である。これは、超低メタルの種族III 星の一生 (Moriya, Langer 2015) にとっては重要な意味を有する。

　４．ＭＥＳＡモデル　

ＭＥＳＡモデル　 　MESA = Modules for Experiments in Stellar Astrophysics (Paxto et al 2011, 2013, 2015, 2018) は恒星進化計算の標準ツールである。最新の物理が 含まれている。Mi = 12 - 24 Mo とし、ZAMS から中心部で炭素が枯渇するまで 計算した。計算パラメターは Chun et al 2018 に従った。それは、ミクシング レングスパラメター αMLP = 2.7, Z = 0.04, オーバーシュ ート fOV = 0.15 で、マスロスは "Dutch" wind (de Jager et al 1988, Vink et al 2001) を採用した。回転は含まない。 　ＭＥＳＡ　と観測の比較　 　モデルが MS を出発してからは、 Teff < 4500 K の星に対し、星震学 計算モデュール GYRE を各ステップごとに適用した。その計算では P = 10 - 10,000 日の動径振動を全て計算した。図８の左は幾つかの Mi に対する結果で ある。図８右側は観測点と比較するためヘリウムが中心で点火した後の経路の みを示す。RSG 寿命の 95 % 以上がそこで過ごされるからである。図８から RSGs の脈動の多くが基本振動であり、短周期側にずれた星が多分第１倍音 モードであることを示す。Heger et al 1997 によると RSGs 脈動は水素の κ メカニズムで励起され、 P ∝ L/M である。 Gough et al 1965 の予想と も合う結果である。 　ＨＲ図　 　図９には HR 図上で MESA モデルと観測 RSGs を比較した。薄青丸＝基本振 動と思われる RSGs ある。星印＝第１倍音ではないかと思われる星が薄青と重 なっていることは、同じ構造の星の振動モードの違いと言う解釈を支持する。 　M-L 関係が緩い　 　既に知られているように RSGs には単一の M-L 関係が存在しない。その結果、 異なる質量の星が同じ光度を有し、図６の PLR の分散の一因になっている。 したがって、PLR の精度には内因性の限界が付随する。

図９．MESA 進化経路の HR-図。灰色点＝観測 RSGs. 星印＝図８で短周期側に ずれた系列の星。抜け青丸＝周期が決まらなかった RSGs.

　５．内因性分散の SN II-P 前駆天体質量推定に及ぼす影響　

SNe II-P/L 前駆星は 18 Mo 以下　 　RSGs が SNe II-P/L 前駆星であるという説は、これらの爆発の前の銀河画像 で確かめられている。最近 15 年間の観測から Smart 2015 は前駆天体質量の 研究をした。その手順は、まず測光等級を輻射等級に直し、恒星モデルを使って 得た Mi-Lfinal 関係から Mi を推定するというものである。その結果、Mi の 上限は 18 Mi となった。この値は RSGs の上限質量 25 - 30 Mo よりずっと低い。 しかし、この推定には、輻射補正値、星周減光、変光等の効果が影響する。 　この後ベイズ推計で影響があるかどうか議論しているが意味があると思えない。

図１０．平均輻射光度 ⟨log(L/Lo)⟩ - ランダム位相輻射光度の関係。 赤丸＝ M31 RSGs。赤棒＝ log(L/Lo)分布の標準偏差。黒点線＝１：１関係。 青線＝Smart 2015 の関係。

　６．結論