
|
平衡状態にある 3 軸不等恒星系の数値モデルを計算した。手続きは次の
4段階に分かれる: (1)軸比 1 : 1.25 : 2 の変形ハッブルモデルの密度分布を選ぶ。回転はしない。 (2)選んだモデルのポテンシャルを計算する。 (3)1500 軌道を計算する。それぞれは約100振動=10億年を被う。軌道は ボックス軌道族とチューブ軌道族の二つに分かれる。 (4)得られた軌道の部分集合の積み重ね、各軌道には適当な星数の重みを 付けて、を行い、各8分象限内の285細胞中の質量に基づく、選んだ密度分布の 再現を探す。 |
主な結論は、 (1)第3段階で計算した軌道の大部分は3つの実質的な積分を伴っていた。 (2)第4段階で見出された数値解の存在は楕円銀河には3軸不等の力学平衡にある ものが実際に存在することを示唆する。 |
|
|
|

2a.密度分布の選択2b.重力ポテンシャルの導出 |
2c.軌道計算2d.付加的有効積分の存在 |
2e.モデル密度分布の再現 |
|
3a.密度分布の選択 |
|
3b.密度分布の導出 |
|
3c.軌道と軌道密度分布の計算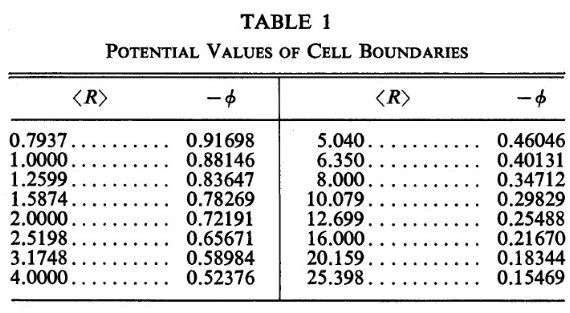 表1. |
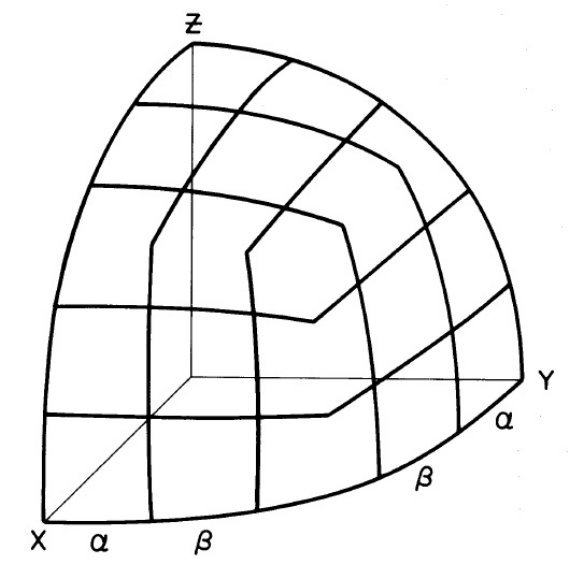 図1. |

|
|
|

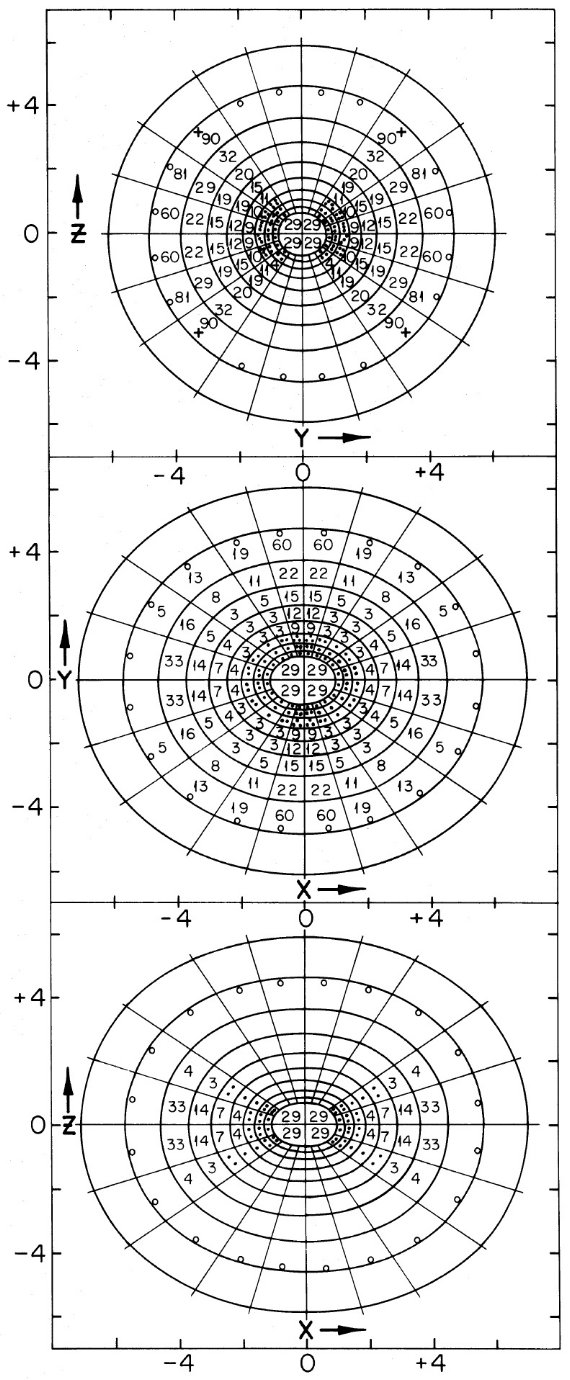 図2. |
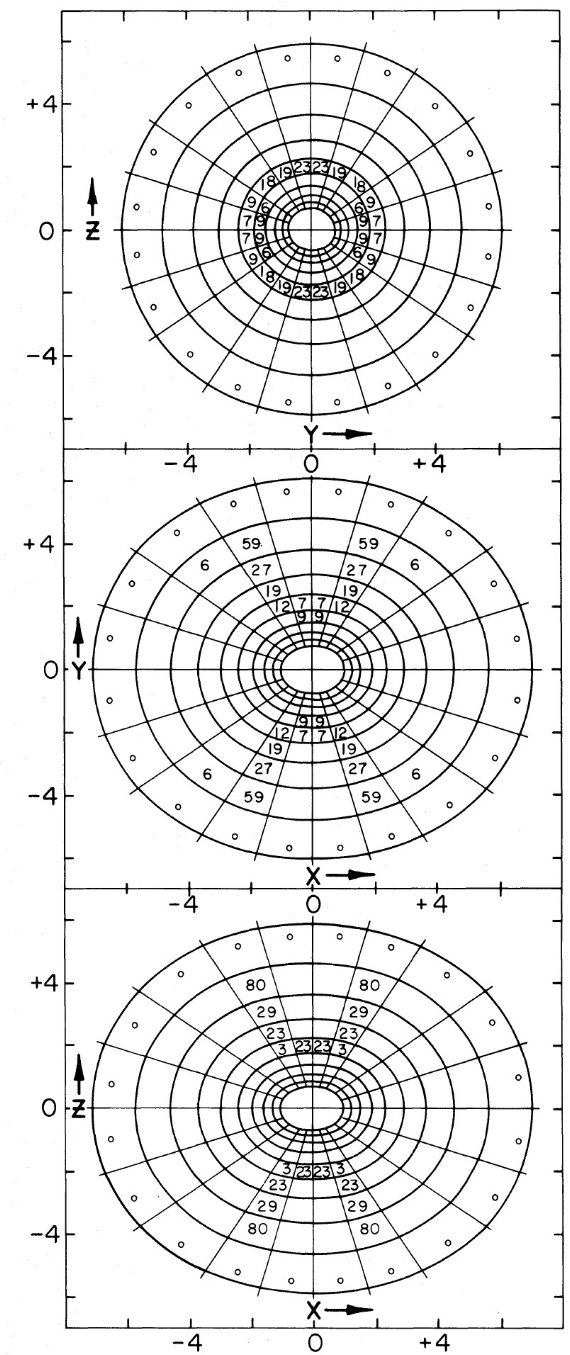 図3. |
3e. 線形法によるモデル構成 |
|

|
|
|

|
|
|
